A Level Mathematics - Questionbank
Functions cover the fundamental concepts of mappings, domains, ranges, and inverses. Students learn to combine, transform, and sketch functions while analyzing their behavior. This topic is essential for understanding mathematical relationships and forms the basis for more advanced studies in algebra and calculus.
Question 1
State the domain and range for the functions represented by these two graphs.
a.
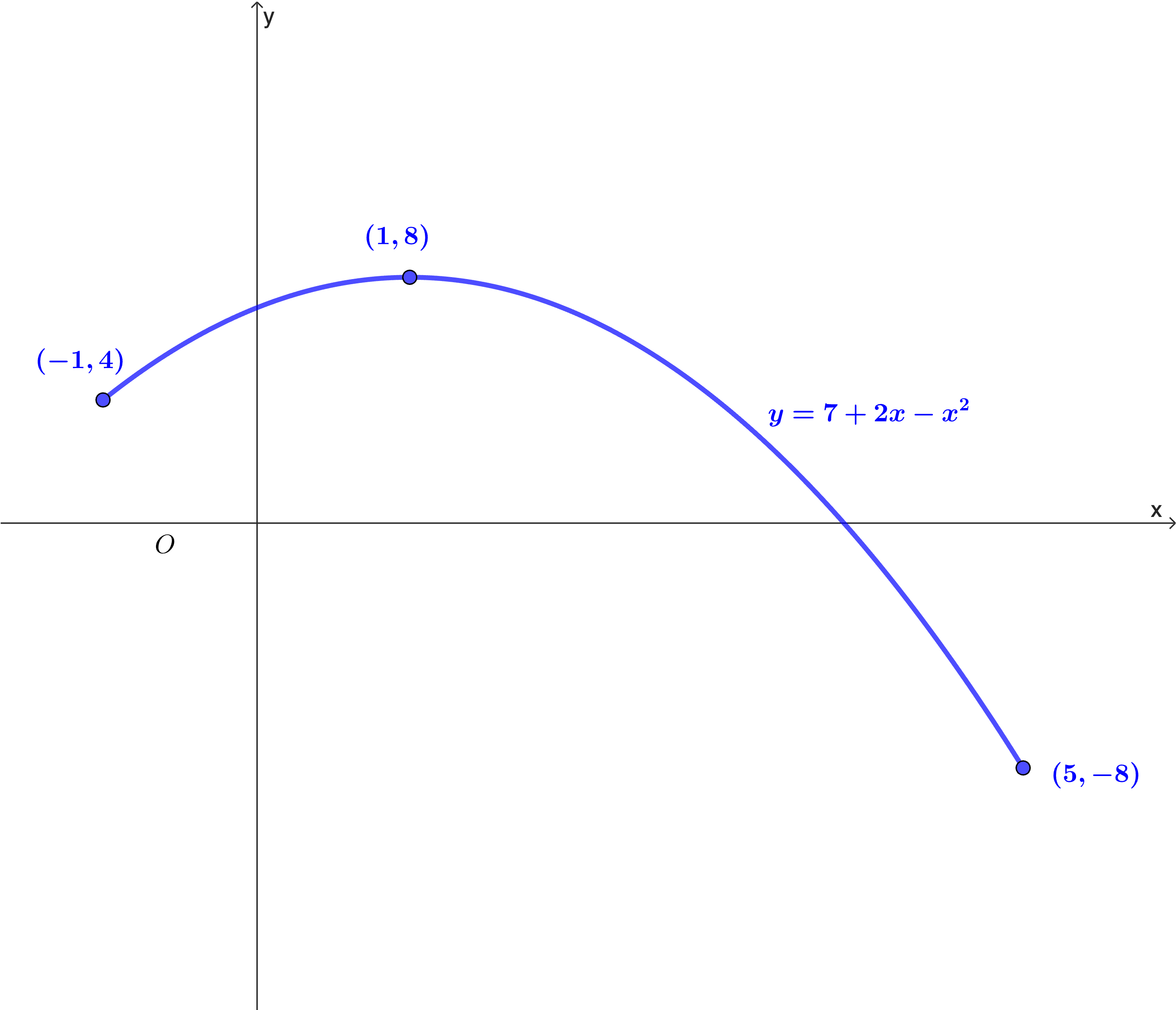
b.
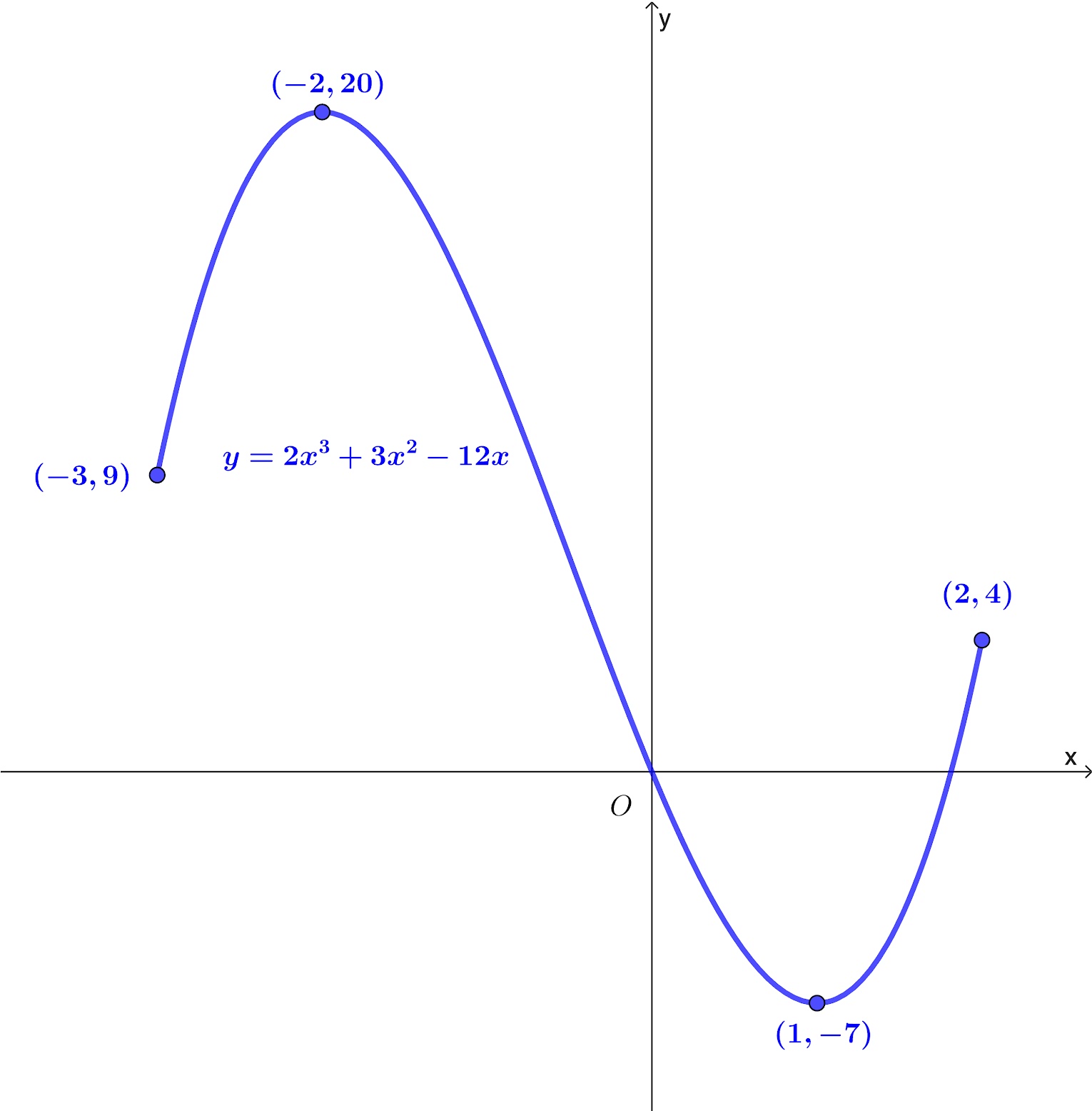
Easy
Mark as Complete
Mark Scheme
Question 2
Find the range for `f:x|->2x^2` for `1<=x<=4`.
Easy
Mark as Complete
Mark Scheme
Question 3
Find the range for `f(x)=frac{12}{x}` for `1<=x<=8`.
Easy
Mark as Complete
Mark Scheme
Question 4
Find the range for `f(x)=1+sqrt{x-4}` for `x>=4`.
Easy
Mark as Complete
Mark Scheme
Question 5
The function `g:x|->5-ax-2x^2`, where a is a constant, is defined for `x in RR`.
Find the range of g in terms of a.
Easy
Mark as Complete
Mark Scheme
Question 6
`f(x)=2x^2-8x+5` for `x in RR`, `0<=x<=k`
a. Express `f(x)` in the form `a(x+b)^2+c`.
b. State the value of `k` for which the graph of `y=f(x)` has a line of symmetry.
c. For your value of `k` from part b, find the range of `f`.
Hard
Mark as Complete
Mark Scheme
Question 7
`f:x|->x^2` for `x in RR`
`g:x|->x+1` for `x in RR`
Express each of the following as a composite function, using only `f` and/or `g`
a. `x|->(x+1)^2`
b. `x|->x^2+2x+2`
c. `x|->x^4+2x^2+1`
Hard
Mark as Complete
Mark Scheme
Question 8
`f(x)=frac{x+5}{2x-1}` for `x in RR`, `x!=frac{1}{2}`
Show that `ff(x)=x`
Easy
Mark as Complete
Mark Scheme
Question 9
`f:x|->(x+1)^3-4` for `x in RR`, `x>=0`
a. Find an expression for `f^-1(x)`.
b. Find the domain and range of `f^-1`.
Easy
Mark as Complete
Mark Scheme
Question 10
`f(x)=frac{1}{x-1}` for `x in RR`, `x!=1`
a. Find an expression for `f^-1(x)`.
b. Show that if `f(x)=f^-1(x)`, then `x^2-x-1=0`.
c. Find the values of `x` for which `f(x)=f^-1(x)`. Give your answer in surd form.
Medium
Mark as Complete
Mark Scheme
Question 11
a. A cubic graph has equation `y=(x+3)(x-2)(x-5)`.
Write, in a similar form, the equation of the graph after a translation of `((2),(0))`.
b. The graph of `y=x^2-4x+1` is translated by the vector `((1),(2))`.
Find, in the form `y=ax^2+bx+c`, the equation of the resulting graph.
Medium
Mark as Complete
Mark Scheme
Question 12
The function `f` is defined by `f(x)=frac{2x}{3x-1}` for `x>frac{1}{3}`.
a. Find an expression for `f^-1(x)`.
b. Show that `frac{2}{3}+frac{2}{3(3x-1)}` can be expressed as `frac{2x}{3x-1}`.
c. State the range of `f`.
Hard
Mark as Complete
Mark Scheme
Question 13
Function `f` and `g` are defined by
`f(x)=4x-2` , for `x in RR`
`g(x)=frac{4}{x+1}` , for `x in RR`, `x!=-1`
a. Find the value of `fg(7)`.
b. Find the values of `x` for which `f^-1(x)=g^-1(x)`.
Hard
Mark as Complete
Mark Scheme
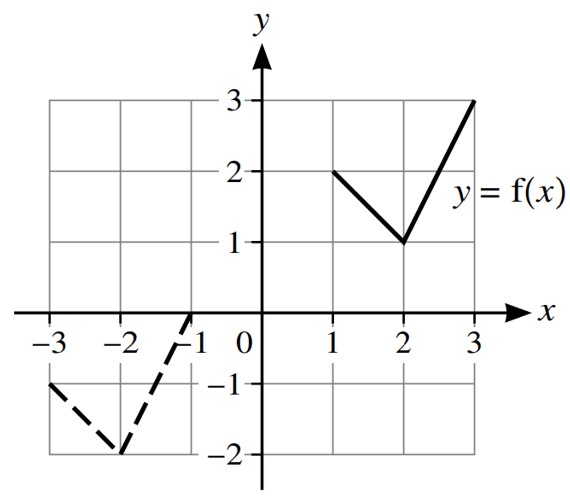
Question 14
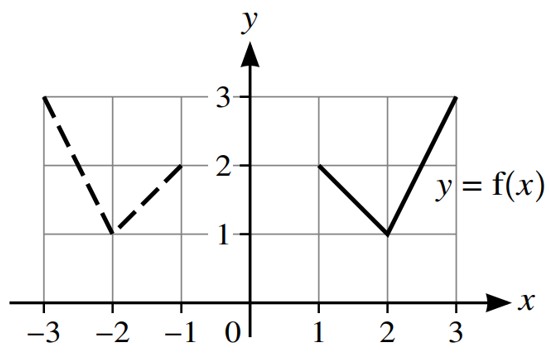
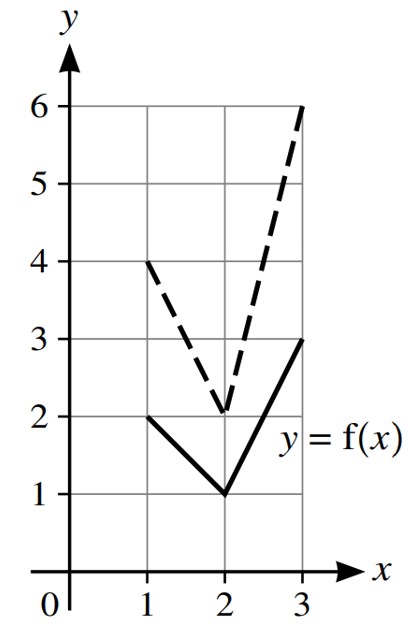
In each of parts a, b and c, the graph shown with solid lines has equation `y=f(x)`. The graph
shown with broken lines is a transformation of `y=f(x)`.
State, in terms of `f`, the equation of the graph shown with broken lines.
a.
b.
c.
Medium
Mark as Complete
Mark Scheme
Question 15
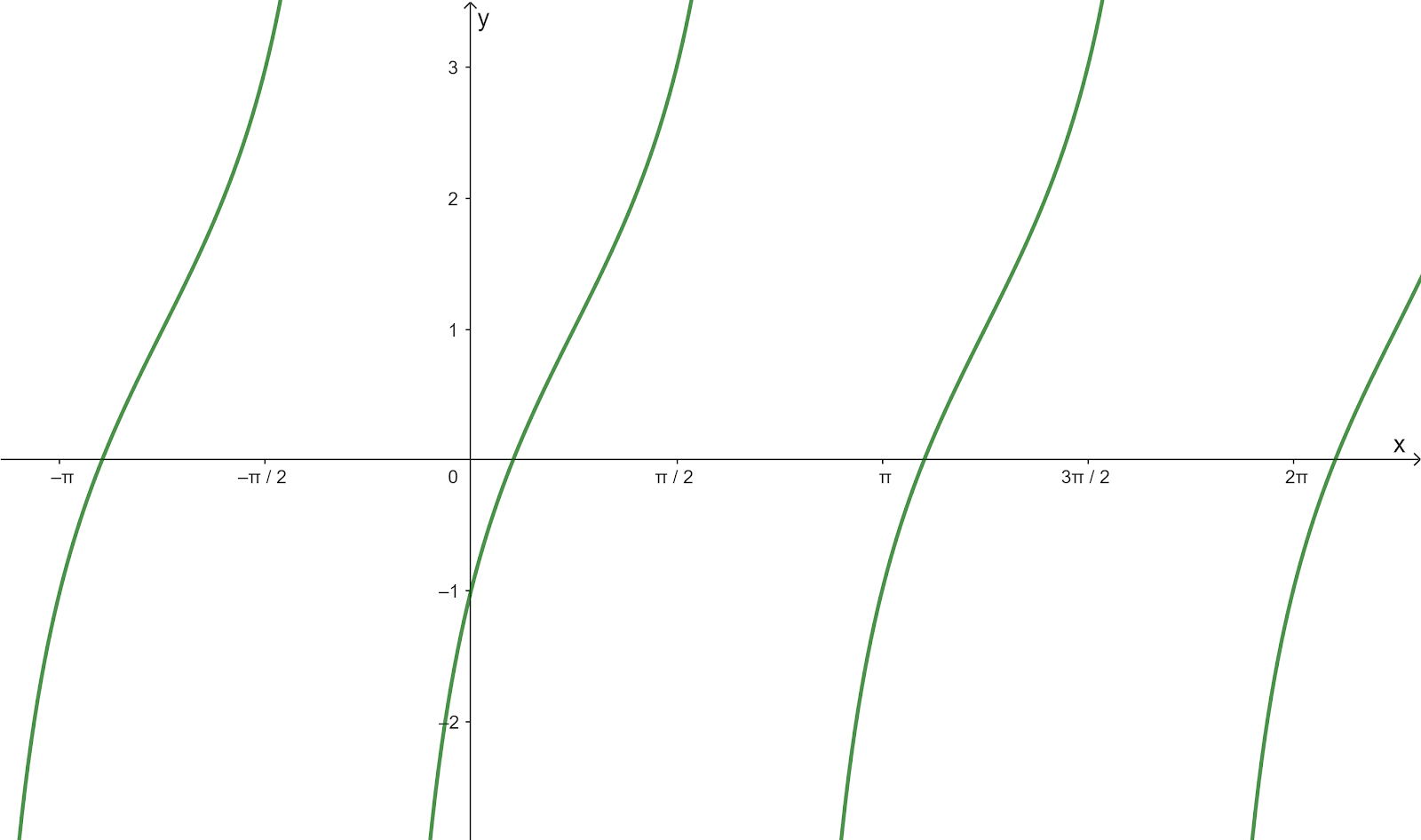
The diagram shows part of the graph of `y=atan(x-b)+c`.
Given that `0 < b < pi`, state the values of the constants a, b and c.
Hard
Mark as Complete
Mark Scheme
Question 16
The graph of `y=f(x)` is transformed to the graph of `y=f(2x)-3`.
a. Describe fully the two single transformations that have been combined to give the resulting transformation.
b. The point P `(5,6)` lies on the transformed curve `y=f(2x)-3`. State the coordinates of the corresponding point on the original curve `y=f(x)`.
Medium
Mark as Complete
Mark Scheme
Question 17
The function `f` is defined by `f(x)=2x^2+3` for `x>=0`
a. Find and simplify an expression for `ff(x)`.
b. Solve the equation `ff(x)=34x^2+19`.
Medium
Mark as Complete
Mark Scheme
Question 18
Functions `f` and `g` are defined as follows:
`f(x)=(x-2)^2-4` for `x>=2`
`g(x)=ax+2` for `x in RR`, where `a` is a constant.
a. State the range of `f`.
b. Find `f^-1(x)`.
c. Give that `a=-frac{5}{3}`, solve the equation `f(x)=g(x)`.
d. Given instead that `ggf^-1(12)=62`, find the possible values of `a`.
Hard
Mark as Complete
Mark Scheme
Question 19
Functions `f` and `g` are both defined for `x in RR` and are given by
`f(x)=x^2-4x+9`
`g(x)=2x^2+4x+12`
a. Express `f(x)` in the form `(x-a)^2+b`.
b. Express `g(x)` in the form `2[(x+c)^2+d]`.
c. Express `g(x)` in the form `kf(x+h)`, where `k` and `h` are integers.
d. Describe fully the two transformations that have been combined to transform the graph of `y=f(x)` to the graph of `y=g(x)`.
Hard
Mark as Complete
Mark Scheme
Question 20
`f(x)=(x+a)^2-a` for `x<=-a`, where `a` is a positive constant
a. Find an expression for `f^-1(x)`.
b. State the domain and the range of the function `f^-1`.
Hard
Mark as Complete
Mark Scheme
Question 1
State the domain and range for the functions represented by these two graphs.
a.

b.

a.
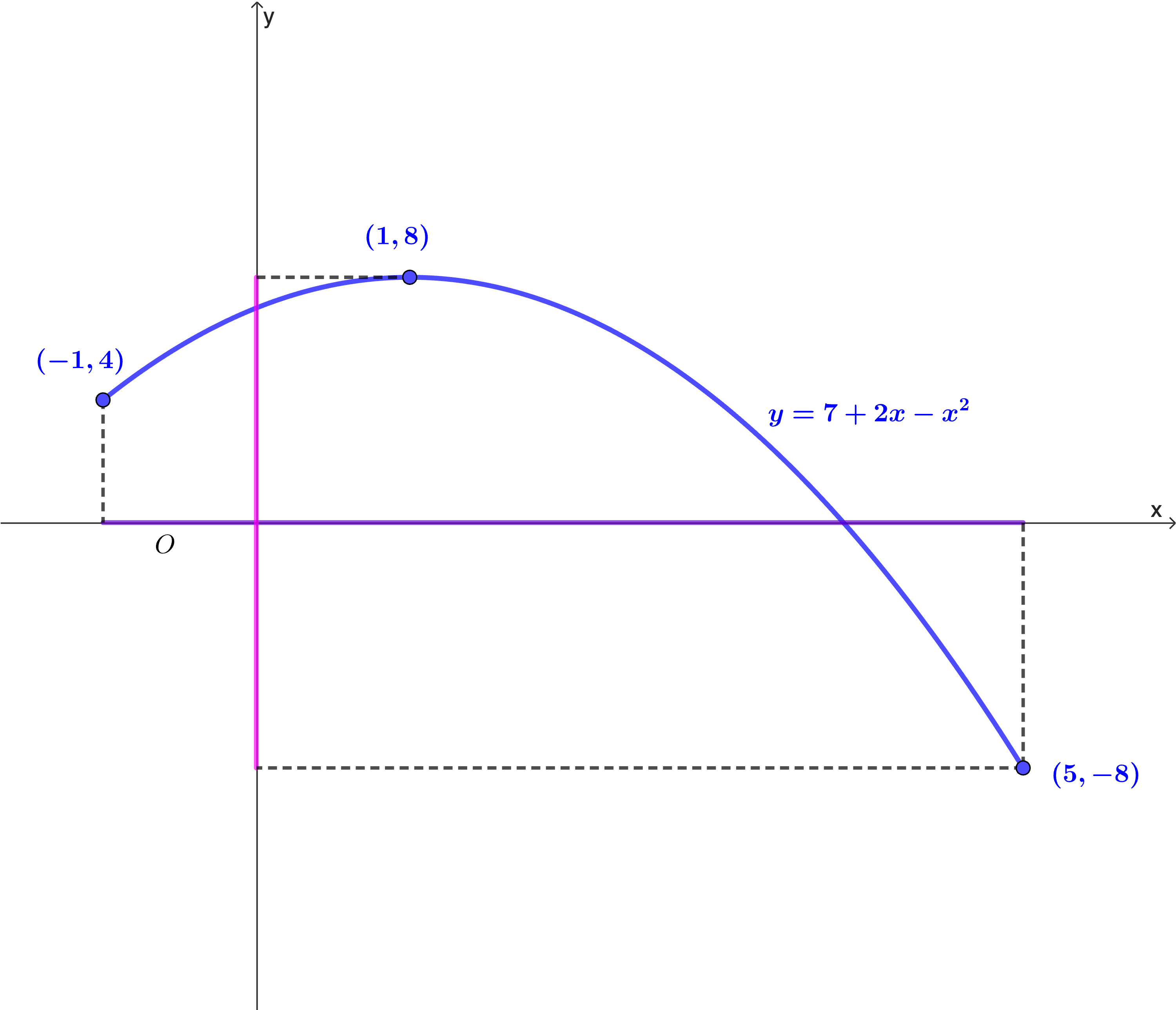
Domain: `x in RR` for `-1<=x<=5`
Range: `f(x) in RR` for `-8<=f(x)<=8`
b.
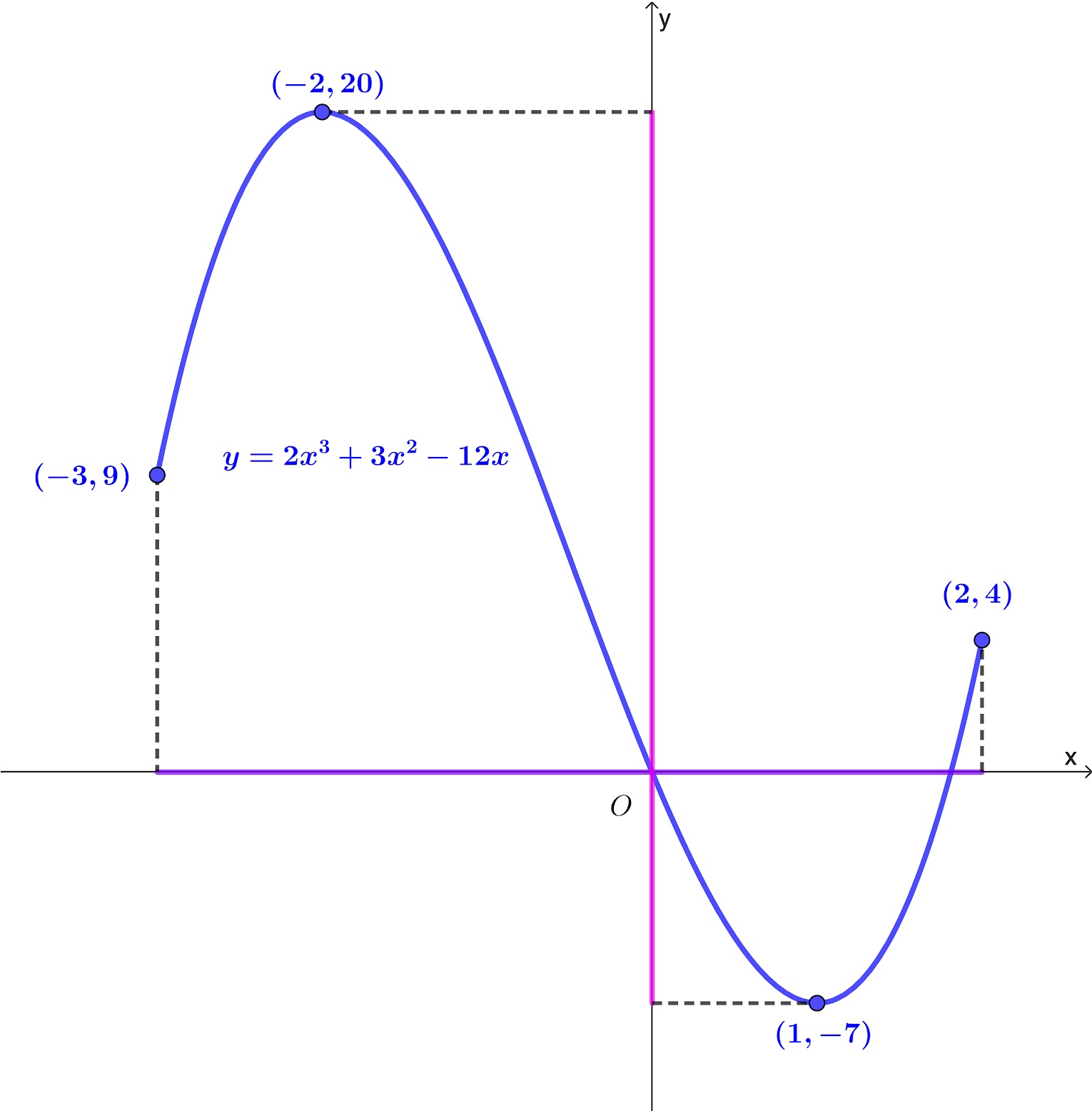
Domain: `x in RR` for `-3<=x<=2`
Range: `f(x) in RR` for `-7<=f(x)<=20`
Question 2
Find the range for `f:x|->2x^2` for `1<=x<=4`.
`f(x)=2x^2` is a quadratic function represented by a `uu` shaped parabola (positive coefficient)
Substitute `x=1`
`f(1)=2(1)^2=2`
Substitute `x=4`
`f(4)=2(4)^2=32`
Final solution
`2<=f(x)<=32`
Question 3
Find the range for `f(x)=frac{12}{x}` for `1<=x<=8`.
`f(x)=frac{12}{x}` is a rational function represented by a hyperbola graph and `x!=0`
Substitute `x=1`
`f(1)=frac{12}{1}=12`
Substitute `x=8`
`f(8)=frac{12}{8}=1.5`
Final solution
`1.5<=f(x)<=12`
Question 4
Find the range for `f(x)=1+sqrt{x-4}` for `x>=4`.
`f(x)=1+sqrt{x-4}` is a square root function represented by an increasing, upward-curve graph
Substitute `x=4`
`f(4)=1+sqrt{4-4}=1`
As x approaches infinity (no upper bound)
`f(x)>=1`
Question 5
The function `g:x|->5-ax-2x^2`, where a is a constant, is defined for `x in RR`.
Find the range of g in terms of a.
The function represented by a `nn` shaped parabola (negative coefficient)
The vertex form of quadratic function `y=a(x-h)^2+k`, where `(h,k)` is the vertex of the parabola
`g(x)=-2x^2-ax+5`
Factorise
`g(x)=-2(x^2+frac{a}{2}x)+5`
The square of half the coefficient `frac{a}{2}`
`frac{a}{2}-:2=frac{a}{4}`
`(frac{a}{4})^2=frac{a^2}{16}`
Add and subtract to the equation
`g(x)=-2(x^2+frac{a}{2}x+frac{a^2}{16}-frac{a^2}{16})+5`
`g(x)=-2(x+frac{a}{4})^2+frac{a^2}{8}+5`
Vertex of the parabola
`(-frac{a}{4},frac{a^2}{8}+5)`
Maximum value of the function is `frac{a^2}{8}+5`
Final solution
`g(x)<=frac{a^2}{8}+5`
Question 6
`f(x)=2x^2-8x+5` for `x in RR`, `0<=x<=k`
a. Express `f(x)` in the form `a(x+b)^2+c`.
b. State the value of `k` for which the graph of `y=f(x)` has a line of symmetry.
c. For your value of `k` from part b, find the range of `f`.
a. The function represented by a `uu` shaped parabola (positive coefficient)
Factorise
`f(x)=2(x^2-4x)+5`
The square of half the coefficient `-4`
`-4-:2=-2`
`(-2)^2=4`
Add and subtract to the expression
`f(x)=2(x^2-4x+4-4)+5`
`f(x)=2(x-2)^2-3`
Vertex of the parabola
`(2,-3)`
b. Vertical line `x=frac{-b}{2a}` that passes through the vertex is the line of symmetry
`x=-frac{(-8)}{2(2)}=2` (without domain restrictions)
For `f(x)=2x^2-8x+5` and `0<=x<=k`
`x=2` is the midpoint between `0` and `k`
Then `k=4`
c. Substitute `x=4`
`f(4)=2(4)^2-8(4)+5=5`
As the vertex of the parabola is when `f(2)=-3`
Final solution
`-3<=x<=5`
Question 7
`f:x|->x^2` for `x in RR`
`g:x|->x+1` for `x in RR`
Express each of the following as a composite function, using only `f` and/or `g`
a. `x|->(x+1)^2`
b. `x|->x^2+2x+2`
c. `x|->x^4+2x^2+1`
a. `fg(x)` means the function `g` acts on `x` first, then `f` acts on the result
`fg(x)=f(x+1)=(x+1)^2`
Final solution is `fg`
b. Rewrite `x^2+2x+2`
`x^2+2x+1+1`
`=(x+1)^2+1`
For `(x+1)^2+1`, function `g(x)=x+1` must acts on `fg(x)=(x+1)^2`
`gfg(x)=g(x+1)^2=(x+1)^2+1`
Final solution is `gfg`
c. Rewrite `x^4+2x^2+1`
`(x^2)^2+2(x^2)+1`
`=(x^2+1)^2`
For `x^2+1`, function `f(x)=x^2` must acts on function `g(x)=x+1`
`gf(x)=g(x^2)=x^2+1`
For `(x^2+1)^2`, function `f(x)=x^2` must acts on `gf(x)=x^2+1`
`fgf(x)=f(x^2+1)=(x^2+1)^2`
Final solution is `fgf`
Question 8
`f(x)=frac{x+5}{2x-1}` for `x in RR`, `x!=frac{1}{2}`
Show that `ff(x)=x`
`ff(x)=f(frac{x+5}{2x-1})`
`=frac{frac{x+5}{2x-1}+5}{2(frac{x+5}{2x-1})-1`
Multiply both the numerator and the denominator by `2x-1`
`frac{x+5+5(2x-1)}{2(x+5)-1(2x-1)}`
`=frac{11x}{11}`
`=x`
Question 9
`f:x|->(x+1)^3-4` for `x in RR`, `x>=0`
a. Find an expression for `f^-1(x)`.
b. Find the domain and range of `f^-1`.
a. `f(x)=(x+1)^3-4`
Write the function in terms of `y`
`y=(x+1)^3-4`
Interchange the `x` and `y` variables
`x=(y+1)^3-4`
Rearrange to make `y` the subject
`x+4=(y+1)^3`
`root(3)(x+4)=y+1`
`y=root(3)(x+4)-1`
Final solution
`f^-1(x)=root(3)(x+4)-1`
b. As function `f` is a cubic function, `f(x)` increases as `x` increases, and reaches `0` when `x=0` (minimum value)
Substitute `x=0`
`f(0)=(0+1)^3-4=-3`
The range of `f` is `f(x)>=-3` so the domain of `f^-1` is `x>=-3`
The domain of `f` is `x>=0` so the range of `f^-1(x)` is `f^-1(x)>=0`
Question 10
`f(x)=frac{1}{x-1}` for `x in RR`, `x!=1`
a. Find an expression for `f^-1(x)`.
b. Show that if `f(x)=f^-1(x)`, then `x^2-x-1=0`.
c. Find the values of `x` for which `f(x)=f^-1(x)`. Give your answer in surd form.
a. Write the function in terms of `y`
`y=frac{1}{x-1}`
Interchange the `x` and `y` variables
`x=frac{1}{y-1}`
Rearrange to make `y` the subject
`x(y-1)=1`
`xy-x=1`
`xy=x+1`
`y=frac{x+1}{x}`
Final solution
`f^-1(x)=frac{x+1}{x}`
b. For `f(x)=f^-1(x)`
`frac{1}{x-1}=frac{x+1}{x}`
Multiply both sides by `x(x-1)`
`x=(x-1)(x+1)`
`x=x^2-1`
`x^2-x-1=0`
c. For `x^2-x-1=0`
Using quadratic formula `x=frac{-b+-sqrt(b^2-4ac}}{2a}`
`x=frac{-(-1)+-sqrt((-1)^2-4(1)(-1)}}{2(1)}`
`x=frac{1+-sqrt5}{2}`
Question 11
a. A cubic graph has equation `y=(x+3)(x-2)(x-5)`.
Write, in a similar form, the equation of the graph after a translation of `((2),(0))`.
b. The graph of `y=x^2-4x+1` is translated by the vector `((1),(2))`.
Find, in the form `y=ax^2+bx+c`, the equation of the resulting graph.
a. The graph of `y=f(x-a)` is a translation of the graph `y=f(x)` by the vector `((a),(0))`
After a translation of `((2),(0))`, the graph of `y=(x+3)(x-2)(x-5)` is replaced all the `x`’s with `x-2`
`y=(x-2+3)(x-2-2)(x-2-5)`
`y=(x+1)(x-4)(x-7)`
b. The graph of `y=f(x-a)+b` is a translation of the graph `y=f(x)` by the vector `((a),(b))`
After a translation of `((1),(2))`, the graph of `y=x^2-4x+1` is replaced all the `x`’s with `x-1`, and add `2` to the resulting function
`y=(x-1)^2-4(x-1)+1+2`
Rewrite
`y=x^2-2x+1-4x+4+1+2`
`y=x^2-6x+8`
Question 12
The function `f` is defined by `f(x)=frac{2x}{3x-1}` for `x>frac{1}{3}`.
a. Find an expression for `f^-1(x)`.
b. Show that `frac{2}{3}+frac{2}{3(3x-1)}` can be expressed as `frac{2x}{3x-1}`.
c. State the range of `f`.
a. `y=frac{2x}{3x-1}`
Interchange the `x` and `y` variables
`x=frac{2y}{3y-1}`
Rearrange to make `y` the subject
`3xy-x=2y`
`y(3x-2)=x`
`y=frac{x}{3x-2}`
Final solution
`f^-1(x)=frac{x}{3x-2}`
b. The common denominator is `3(3x-1)`
`frac{2(3x-1)}{3(3x-1)}+frac{2}{3(3x-1)}`
`=frac{2(3x-1)+2}{3(3x-1)}`
`=frac{6x}{3(3x-1)}`
`=frac{2x}{3x-1}`
c. For `f(x)=frac{2x}{3x-1}`
`f(x)=frac{2}{3}+frac{2}{3(3x-1)}`
`f(x)=frac{2}{3}(1+frac{1}{3x-1})` (1)
And for `x>frac{1}{3}`
`3x>1`
`3x-1>0`
So `frac{1}{3x-1}` approach `0` as `x` increase
Substitute into (1)
`f(x)=frac{2}{3}(1+0)`
The range of `f` is `f(x)>frac{2}{3}`
Question 13
Function `f` and `g` are defined by
`f(x)=4x-2` , for `x in RR`
`g(x)=frac{4}{x+1}` , for `x in RR`, `x!=-1`
a. Find the value of `fg(7)`.
b. Find the values of `x` for which `f^-1(x)=g^-1(x)`.
a. `g(7)=frac{4}{(7)+1}=frac{4}{8}=frac{1}{2}`
`fg(x)` means the function `g` acts on `x` first, then `f` acts on the result
`fg(7)=f(frac{1}{2})=4(frac{1}{2})-2=0`
b. For `f(x)=4x-2`
`y=4x-2`
Interchange the `x` and `y` variables
`x=4y-2`
Rearrange to make `y` the subject
`4y=x+2`
`y=frac{x+2}{4}`
Then `f^-1(x)=frac{x+2}{4}`
For `g(x)=frac{4}{x+1}`
`y=frac{4}{x+1}`
Interchange the `x` and `y` variables
`x=frac{4}{y+1}`
Rearrange to make `y` the subject
`x(y+1)=4`
`y+1=frac{4}{x}`
`y=frac{4-x}{x}`
Then `g^-1(x)=frac{4-x}{x}`
`f^-1(x)=g^-1(x)`
`frac{x+2}{4}=frac{4-x}{x}`
`x^2+2x=16-4x`
Question 14
In each of parts a, b and c, the graph shown with solid lines has equation `y=f(x)`. The graph
shown with broken lines is a transformation of `y=f(x)`.
State, in terms of `f`, the equation of the graph shown with broken lines.
a.

b.

c.

a. The graph shown with broken lines is a reflection of the graph `y=f(x)` in the y-axis
Then `y=f(-x)`
b. The graph shown with broken lines is a stretch of `y=f(x)`, stretch factor `2`, parallel to the y-axis
Then `y=2f(x)`
c. The graph shown with broken lines is a translation of `y=f(x)` by the vector `((-4),(-3))`
Then `y=f(x+4)-3`
Question 15

The diagram shows part of the graph of `y=atan(x-b)+c`.
Given that `0 < b < pi`, state the values of the constants a, b and c.
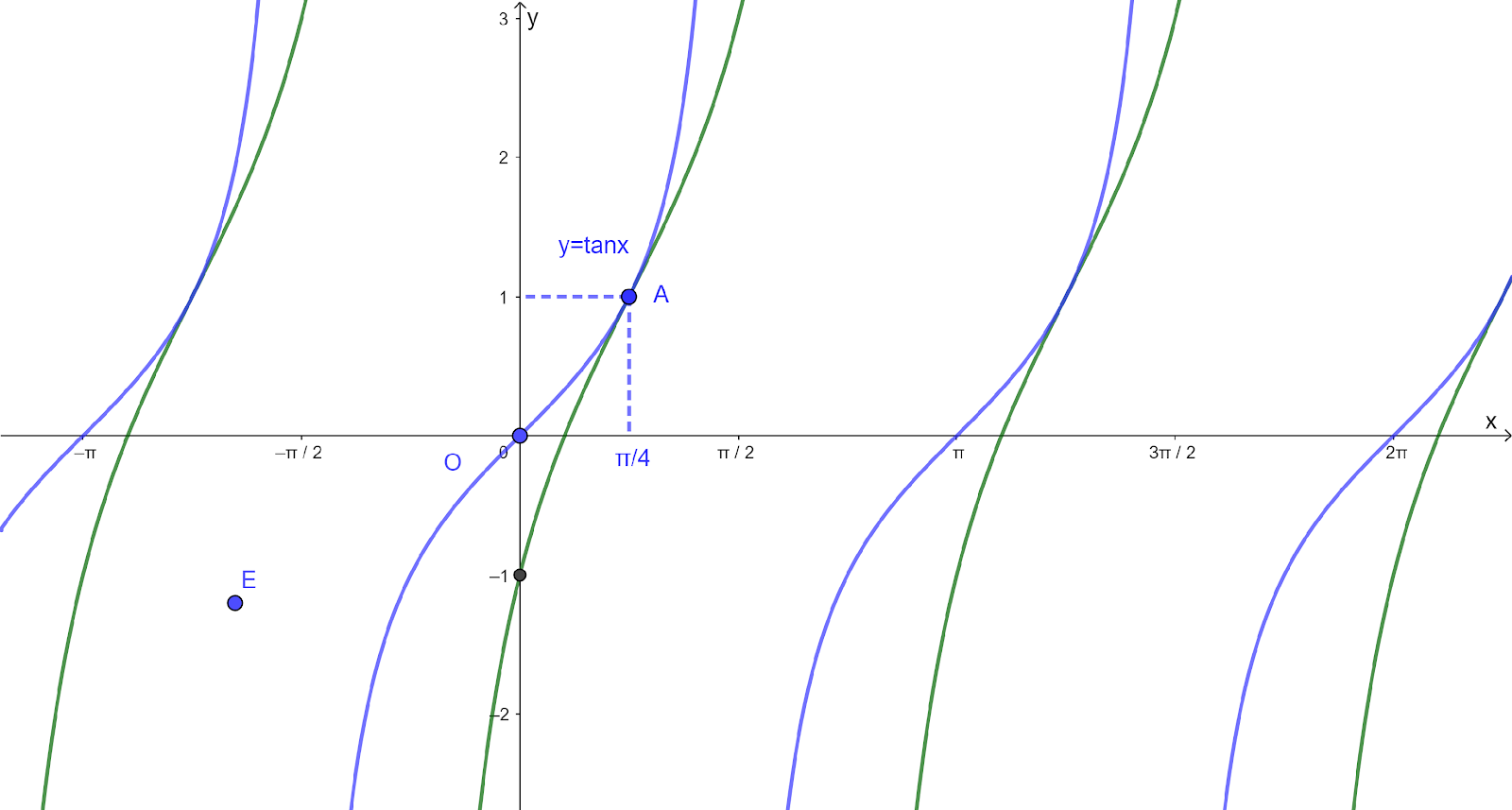
Center point O `(0,0)` from the original graph `y=tanx` is translated into point A `(frac{pi}{4},1)`
Using the tangent function `y=atan(x-b)+c`
`b=frac{pi}{4}` (the horizontal translation parallel to the x-axis)
`c=1` (the vertical translation of parallel to the y-axis)
For `y=atan(x-frac{pi}{4})+1`, substitute `x=0` and `y=-1`
`-1=atan(0-frac{pi}{4})+1`
`-2=a(-1)`
`a=2` (the amplitude)
Then `y=2tan(x-frac{pi}{4})+1`
Question 16
The graph of `y=f(x)` is transformed to the graph of `y=f(2x)-3`.
a. Describe fully the two single transformations that have been combined to give the resulting transformation.
b. The point P `(5,6)` lies on the transformed curve `y=f(2x)-3`. State the coordinates of the corresponding point on the original curve `y=f(x)`.
a. The graph of `y=f(2x)-3` is a stretch of `y=f(x)`, stretch factor `frac{1}{2}`, parallel to the x-axis, and followed by a translation by the vector `((0),(-3))`.
b. The point `(x,y)` lies on the original curve `y=f(x)`
After transformation, the point `(x,y)` changes to the new point `(2x,y+3)`
Substitute the point P `(5,6)` gives the coordinates `(2xx5,6+3)`
`=(10,9)`
Question 17
The function `f` is defined by `f(x)=2x^2+3` for `x>=0`
a. Find and simplify an expression for `ff(x)`.
b. Solve the equation `ff(x)=34x^2+19`.
a. `ff(x)=2(2x^2+3)^2+3`
`=2(4x^4+12x^2+9)+3`
`=8x^4+24x^2+18+3`
`=8x^4+24x^2+21`
b. For `ff(x)=34x^2+19`
`8x^4+24x^2+21=34x^2+19`
`8x^4-10x^2+2=0`
`2(x^2-1)(4x^2-1)=0`
`x^2-1=0` or `4x^2-1=0`
`x^2=1` or `x^2=frac{1}{4}`
`x=+-1` or `x=+-frac{1}{2}`
Final solution
`x=1` or `x=frac{1}{2}` (as `x>=0`)
Question 18
Functions `f` and `g` are defined as follows:
`f(x)=(x-2)^2-4` for `x>=2`
`g(x)=ax+2` for `x in RR`, where `a` is a constant.
a. State the range of `f`.
b. Find `f^-1(x)`.
c. Give that `a=-frac{5}{3}`, solve the equation `f(x)=g(x)`.
d. Given instead that `ggf^-1(12)=62`, find the possible values of `a`.
a. The function represented by a `uu` shaped parabola
Substitute `x=2`
`f(2)=(2-2)^2-4=-4`
Range: `f(x)>=-4`
b. For `f(x)=(x-2)^2-4`
`y=(x-2)^2-4`
Interchange the `x` and `y` variables
`x=(y-2)^2-4`
Rearrange to make `y` the subject
`(y-2)^2=x+4`
`y-2=+-sqrt(x+4)`
`y=+-sqrt(x+4)+2`
`f^-1(x)=sqrt(x+4)+2` (as `x>=2`)
c. For `f(x)=g(x)`
`(x-2)^2-4=-frac{5}{3}x+2`
`x^2-4x+4-4=-frac{5}{3}x+2`
`x^2-frac{7}{3}x-2=0`
Using quadratic formula `x=frac{-b+-sqrt(b^2-4ac)}{2a}`
`x=frac{-(-frac{7}{3})+-sqrt((-frac{7}{3})^2-4(1)(-2))}{2(1)}`
`x=3` or `x=-frac{2}{3}`
Final solution
`x=3` (as `x>=2`)
d. For `f^-1(x)=sqrt(x+4)+2` and `g(x)=ax+2`
`f^-1(12)=sqrt(12+4)+2=6`
`gf^-1(12)=6a+2`
For `ggf^-1(12)=62`
`ggf^-1(12)=a(6a+2)+2=62`
`6a^2+2a+2-62=0`
`6a^2+2a-60=0`
`a=-frac{10}{3}` or `a=3`
Question 19
Functions `f` and `g` are both defined for `x in RR` and are given by
`f(x)=x^2-4x+9`
`g(x)=2x^2+4x+12`
a. Express `f(x)` in the form `(x-a)^2+b`.
b. Express `g(x)` in the form `2[(x+c)^2+d]`.
c. Express `g(x)` in the form `kf(x+h)`, where `k` and `h` are integers.
d. Describe fully the two transformations that have been combined to transform the graph of `y=f(x)` to the graph of `y=g(x)`.
a. `f(x)=x^2-4x+9`
`=x^2-4x+4-4+9`
`=(x^2-4x+4)+5`
`=(x-2)^2+5`
b. `g(x)=2x^2+4x+12`
`=2(x^2+2x+6)`
`=2(x^2+2x+1-1+6)`
`=2[(x^2+2x+1)-1+6]`
`=2[(x+1)^2+5]`
c. Substitute `x=x+3` into `f(x)=(x-2)^2+5`
`f(x+3)=(x+3-2)^2+5=(x+1)^2+5`
Then `g(x)=2[(x+1)^2+5]=2f(x+3)`
`k=2` and `h=3`
d. The graph of `g(x)=2f(x+3)` is a translation of the graph `y=f(x)` by the vector `((-3),(0))`
After a translation of `((-3),(0))`, the graph is stretched by factor `2` parallel to the y-axis.
Question 20
`f(x)=(x+a)^2-a` for `x<=-a`, where `a` is a positive constant
a. Find an expression for `f^-1(x)`.
b. State the domain and the range of the function `f^-1`.
a. For `f(x)=(x+a)^2-a`
`y=(x+a)^2-a`
Interchange the `x` and `y` variables
`x=(y+a)^2-a`
Rearrange to make `y` the subject
`(y+a)^2=x+a`
`y+a=+-sqrt(x+a)`
`y=+-sqrt(x+a)-a`
`f^-1(x)=-sqrt(x+a)-a` (as `x<=-a`)
b. Substitute `x=-a`
`f(-a)=(-a+a)^2-a=-a`
The range of `f` is `f(x)>=-a` so the domain of `f^-1` is `x>=-a`
The domain of `f` is `x<=-a` so the range of `f^-1(x)` is `f^-1(x)<=-a`
Question 1
State the domain and range for the functions represented by these two graphs.
a.

b.

Question 2
Find the range for `f:x|->2x^2` for `1<=x<=4`.
Question 3
Find the range for `f(x)=frac{12}{x}` for `1<=x<=8`.
Question 4
Find the range for `f(x)=1+sqrt{x-4}` for `x>=4`.
Question 5
The function `g:x|->5-ax-2x^2`, where a is a constant, is defined for `x in RR`.
Find the range of g in terms of a.
Question 6
`f(x)=2x^2-8x+5` for `x in RR`, `0<=x<=k`
a. Express `f(x)` in the form `a(x+b)^2+c`.
b. State the value of `k` for which the graph of `y=f(x)` has a line of symmetry.
c. For your value of `k` from part b, find the range of `f`.
Question 7
`f:x|->x^2` for `x in RR`
`g:x|->x+1` for `x in RR`
Express each of the following as a composite function, using only `f` and/or `g`
a. `x|->(x+1)^2`
b. `x|->x^2+2x+2`
c. `x|->x^4+2x^2+1`
Question 8
`f(x)=frac{x+5}{2x-1}` for `x in RR`, `x!=frac{1}{2}`
Show that `ff(x)=x`
Question 9
`f:x|->(x+1)^3-4` for `x in RR`, `x>=0`
a. Find an expression for `f^-1(x)`.
b. Find the domain and range of `f^-1`.
Question 10
`f(x)=frac{1}{x-1}` for `x in RR`, `x!=1`
a. Find an expression for `f^-1(x)`.
b. Show that if `f(x)=f^-1(x)`, then `x^2-x-1=0`.
c. Find the values of `x` for which `f(x)=f^-1(x)`. Give your answer in surd form.
Question 11
a. A cubic graph has equation `y=(x+3)(x-2)(x-5)`.
Write, in a similar form, the equation of the graph after a translation of `((2),(0))`.
b. The graph of `y=x^2-4x+1` is translated by the vector `((1),(2))`.
Find, in the form `y=ax^2+bx+c`, the equation of the resulting graph.
Question 12
The function `f` is defined by `f(x)=frac{2x}{3x-1}` for `x>frac{1}{3}`.
a. Find an expression for `f^-1(x)`.
b. Show that `frac{2}{3}+frac{2}{3(3x-1)}` can be expressed as `frac{2x}{3x-1}`.
c. State the range of `f`.
Question 13
Function `f` and `g` are defined by
`f(x)=4x-2` , for `x in RR`
`g(x)=frac{4}{x+1}` , for `x in RR`, `x!=-1`
a. Find the value of `fg(7)`.
b. Find the values of `x` for which `f^-1(x)=g^-1(x)`.
Question 14
In each of parts a, b and c, the graph shown with solid lines has equation `y=f(x)`. The graph
shown with broken lines is a transformation of `y=f(x)`.
State, in terms of `f`, the equation of the graph shown with broken lines.
a.

b.

c.

Question 15

The diagram shows part of the graph of `y=atan(x-b)+c`.
Given that `0 < b < pi`, state the values of the constants a, b and c.
Question 16
The graph of `y=f(x)` is transformed to the graph of `y=f(2x)-3`.
a. Describe fully the two single transformations that have been combined to give the resulting transformation.
b. The point P `(5,6)` lies on the transformed curve `y=f(2x)-3`. State the coordinates of the corresponding point on the original curve `y=f(x)`.
Question 17
The function `f` is defined by `f(x)=2x^2+3` for `x>=0`
a. Find and simplify an expression for `ff(x)`.
b. Solve the equation `ff(x)=34x^2+19`.
Question 18
Functions `f` and `g` are defined as follows:
`f(x)=(x-2)^2-4` for `x>=2`
`g(x)=ax+2` for `x in RR`, where `a` is a constant.
a. State the range of `f`.
b. Find `f^-1(x)`.
c. Give that `a=-frac{5}{3}`, solve the equation `f(x)=g(x)`.
d. Given instead that `ggf^-1(12)=62`, find the possible values of `a`.
Question 19
Functions `f` and `g` are both defined for `x in RR` and are given by
`f(x)=x^2-4x+9`
`g(x)=2x^2+4x+12`
a. Express `f(x)` in the form `(x-a)^2+b`.
b. Express `g(x)` in the form `2[(x+c)^2+d]`.
c. Express `g(x)` in the form `kf(x+h)`, where `k` and `h` are integers.
d. Describe fully the two transformations that have been combined to transform the graph of `y=f(x)` to the graph of `y=g(x)`.
Question 20
`f(x)=(x+a)^2-a` for `x<=-a`, where `a` is a positive constant
a. Find an expression for `f^-1(x)`.
b. State the domain and the range of the function `f^-1`.