A Level Mathematics - Questionbank
Coordinate geometry focuses on equations of straight lines, including concepts like gradients, midpoints, and distances between points. Students explore the geometry of circles, deriving equations and solving related problems. This topic builds a solid foundation for analyzing geometric relationships in a Cartesian plane, essential for advanced applications in mathematics.
Question 1
In triangle ABC, the midpoints of the sides AB, BC and AC are `(1,4)`, `(2,0)` and `(-4,1)`, respectively. Find the coordinates of points A, B and C.
Easy
Mark as Complete
Mark Scheme
Question 2
Three points have coordinates A `(7,4)`, B `(19,8)` and C `(k,2k)`. Find the value of the constant `k` for which:
a. C lies on the line that passes through the points A and B
b. angle CAB is `90°`
Easy
Mark as Complete
Mark Scheme
Question 3
The coordinates of triangle ABC are A `(-7,3)`, B `(3,-7)` and C `(8,8)`. P is the foot of the perpendicular from B to AC.
a. Find the equation of the line BP.
b. Find the coordinates of P.
c. Find the lengths of AC and BP.
d. Use your answers to part c to find the area of triangle ABC.
Easy
Mark as Complete
Mark Scheme
Question 4
A circle has radius `10` units and passes through the point `(5, -16)`. The x-axis is a tangent to the circle. Find the possible equations of the circle.
Easy
Mark as Complete
Mark Scheme
Question 5
The line `2y-x=12` intersects the circle `x^2+y^2-10x-12y+36=0` at the points A and B.
a. Find the coordinates of the points A and B.
b. Find the equation of the perpendicular bisector of AB.
c. The perpendicular bisector of AB intersects the circle at the points P and Q. Find the exact coordinates of P and Q.
d. Find the exact area of quadrilateral APBQ.
Hard
Mark as Complete
Mark Scheme
Question 6
Show that the circles `x^2+y^2=25` and `x^2+y^2-24x-18y` touch each other. Find the coordinates of the point where they touch.
Easy
Mark as Complete
Mark Scheme
Question 7
The curve `y=3sqrt(x-2)` and the line `3x-4y+3=0` intersect at the points P and Q. Find the length of PQ.
Easy
Mark as Complete
Mark Scheme
Question 8
The line with gradient `-2` passing through the point P `(3t,2t)` intersects the x-axis at A and the y-axis at B.
a. Find the area of triangle AOB in terms of `t`.
b. The line through P perpendicular to AB intersects the x-axis at C.
Show that the mid-point of PC lies on the line `y=x`.
Medium
Mark as Complete
Mark Scheme
Question 9
The point A has coordinates `(-1,6)` and the point B has coordinates `(7,2)`.
a. Find the equation of the perpendicular bisector of AB, giving your answer in the form `y=mx+c`.
b. A point C on the perpendicular bisector has coordinates (p,q). The distance OC is `2` units, where O is the origin. Write down two equations involving p and q and hence find the coordinates of the possible positions of C.
Easy
Mark as Complete
Mark Scheme
Question 10
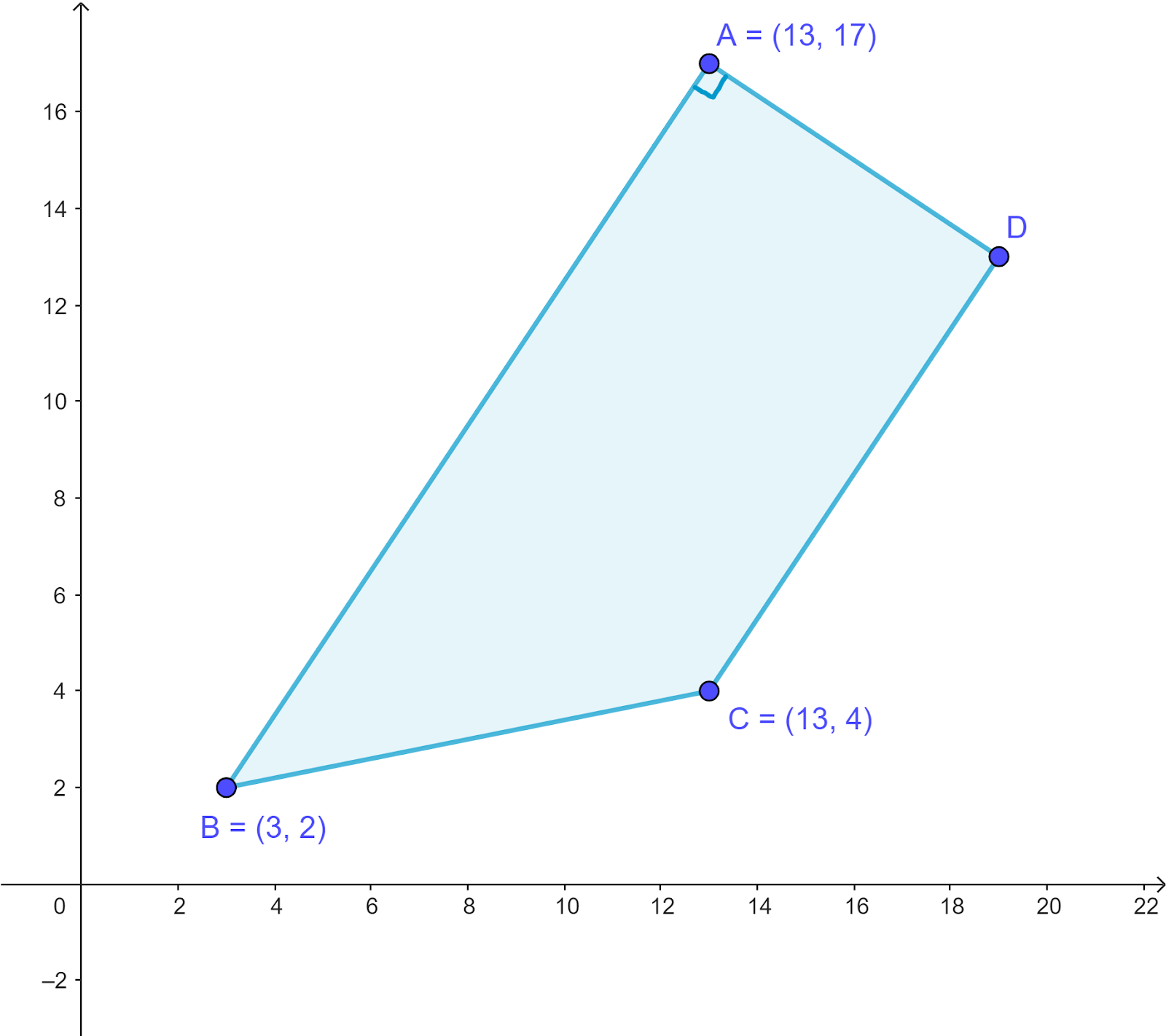
ABCD is a trapezium with AB parallel to DC and angle BAD `=90°`.
a. Calculate the coordinates of D.
b. Calculate the area of trapezium ABCD.
Easy
Mark as Complete
Mark Scheme
Question 11
The equation of a circle is `x^2+y^2-8x+4y+4=0`.
a. Find the radius of the circle and the coordinates of its centre.
b. Find the x-coordinates of the points where the circle crosses the x-axis, giving your answers in exact form.
c. Show that the point A `(6,2sqrt3-2)` lies on the circle.
d. Show that the equation of the tangent to the circle at A is `sqrt3x+3y=12sqrt3-6`.
Hard
Mark as Complete
Mark Scheme
Question 12
Two points A and B have coordinates `(1,3)` and `(9,-1)` respectively. The perpendicular bisector of AB intersects the y-axis at the point C. Find the coordinates of C.
Easy
Mark as Complete
Mark Scheme
Question 13
The diagram shows a trapezium ABCD in which the coordinates of A, B and C are `(4,0)`, `(0,2)` and `(h,3h)` respectively. The lines BC and AD are parallel, angle ABC `=90°` and CD is parallel to the x-axis.
a. Find, by calculation, the value of h.
b. Hence find the coordinates of D.
Easy
Mark as Complete
Mark Scheme
Question 14
The equation of a circle with centre C is `x^2+y^2-8x+4y-5=0`.
a. Find the radius of the circle and the coordinates of C.
b. The point P `(1,2)` lies on the circle. Show that the equation of the tangent to the circle at P is `4y=3x+5`.
c. The point Q also lies on the circle and PQ is parallel to the x-axis. Write down the coordinates of Q.
d. The tangents to the circle at P and Q meet at T. Find the coordinates of T.
Hard
Mark as Complete
Mark Scheme
Question 15
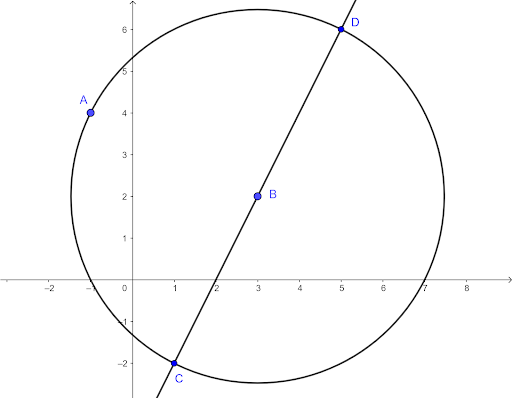
The diagram shows a circle with centre A passing through the point B. A second circle has centre B and passes through A. The tangent at B to the first circle intersects the second circle at C and D.
The coordinates of A are `(-1,4)` and the coordinates of B are `(3,2)`.
a. Find the equation of the tangent CBD.
b. Find an equation of the circle with centre B.
c. Find, by calculation, the x-coordinates of C and D.
Easy
Mark as Complete
Mark Scheme
Question 16
The line `y=2x+5` intersects the circle with equation `x^2+y^2=20` at A and B.
a. Find the coordinates of A and B in surd form and hence find the exact length of the chord AB.
b. A straight line through the point `(10,0)` with gradient m is a tangent to the circle. Find the two possible values of m.
Medium
Mark as Complete
Mark Scheme
Question 17
a. A circle with centre `(5,2)` passes through the point `(7,5)`. Find an equation of the circle.
b. The line intersects the circle at A and B. Find the exact length of the chord AB.
Easy
Mark as Complete
Mark Scheme
Question 18
A line has equation `y=3x+k` and a curve has equation `y=x^2+kx+6`, where k is a constant.
Find the set of values of k for which the line and curve have two distinct points of intersection.
Medium
Mark as Complete
Mark Scheme
Question 19
The equation of a circle is `x^2+y^2+ax+by-12=0`. The points A `(1,1)` and B `(2,-6)` lie on the circle.
a. Find the values of a and b and hence find the coordinates of the centre of the circle.
b. Find the equation of the tangent to the circle at the point A, giving your answer in the form `px+qy=k`, where p, q and k are integers.
Medium
Mark as Complete
Mark Scheme
Question 20
The equation of a circle is `(x-a)^2+(y-3)^2=20`. The line `y=frac{1}{2}x+6` is a tangent to the circle at the point P.
a. Show that one possible value of a is 4 and find the other possible value.
b. For a `= 4`, find the equation of the normal to the circle at P.
c. For a `= 4`, find the equations of the two tangents to the circle which are parallel to the normal found in (b).
Hard
Mark as Complete
Mark Scheme
Question 1
In triangle ABC, the midpoints of the sides AB, BC and AC are `(1,4)`, `(2,0)` and `(-4,1)`, respectively. Find the coordinates of points A, B and C.
For A `(x_1,y_1)`, B `(x_2,y_2)`, and C `(x_3,y_3)`
Midpoint of AB
`(frac{x_1+x_2}{2},frac{y_1+y_2}{2})=(1,4)`
`frac{x_1+x_2}{2}=1` and `frac{y_1+y_2}{2}=4`
`x_1+x_2=2` and `y_1+y_2=8`
Midpoint of BC
`(frac{x_2+x_3}{2},frac{y_2+y_3}{2})=(2,0)`
`frac{x_2+x_3}{2}=2` and `frac{y_2+y_3}{2}=0`
`x_2+x_3=4` and `y_2+y_3=0`
Midpoint of AC
`(frac{x_1+x_3}{2},frac{y_1+y_3}{2})=(-4,1)`
`frac{x_1+x_3}{2}=-4` and `frac{y_1+y_3}{2}=1`
`x_1+x_3=-8` and `y_1+y_3=2`
Subtract `x_1+x_2=2` and `x_2+x_3=4`
`x_1-x_3=-2`
Add `x_1-x_3=-2` and `x_1+x_3=-8`
`2x_1=-10`
`x_1=-5`
Then `x_2=7` and `x_3=-3`
Subtract `y_2+y_3=0` and `y_1+y_2=8`
`y_1-y_3=8`
Add `y_1-y_3=8` and `y_1+y_3=2`
`2y_1=10`
`y_1=5`
Then `y_2=3` and `y_3=-3`
Final solution
A `(−5,5)`, B `(7,3)`, and C `(-3,-3)`
Question 2
Three points have coordinates A `(7,4)`, B `(19,8)` and C `(k,2k)`. Find the value of the constant `k` for which:
a. C lies on the line that passes through the points A and B
b. angle CAB is `90°`
a. As A, B, and C lie on the same line, they are collinear
Gradient of AB = gradient of BC
`frac{8-4}{19-7}=frac{2k-8}{k-19}`
`frac{1}{3}=frac{2k-8}{k-19}`
Cross-multiply
`1(k-19)=3(2k-8)`
`k-19=6k-24`
`5k=5``frac{2k-4}{k-7}xxfrac{1}{3}=-1`
`k=1`
b. Since angle CAB = `90°`, gradient of CA x gradient of AB = `-1`
`frac{2k-4}{k-7}xxfrac{8-4}{19-7}=-1`
`frac{2k-4}{k-7}xxfrac{1}{3}=-1`
`frac{2k-4}{3k-21}=-1`
Cross-multiply
`2k-4=-1(3k-21)`
`2k-4=-3k+21`
`5k=25`
`k=5`
Question 3
The coordinates of triangle ABC are A `(-7,3)`, B `(3,-7)` and C `(8,8)`. P is the foot of the perpendicular from B to AC.
a. Find the equation of the line BP.
b. Find the coordinates of P.
c. Find the lengths of AC and BP.
d. Use your answers to part c to find the area of triangle ABC.
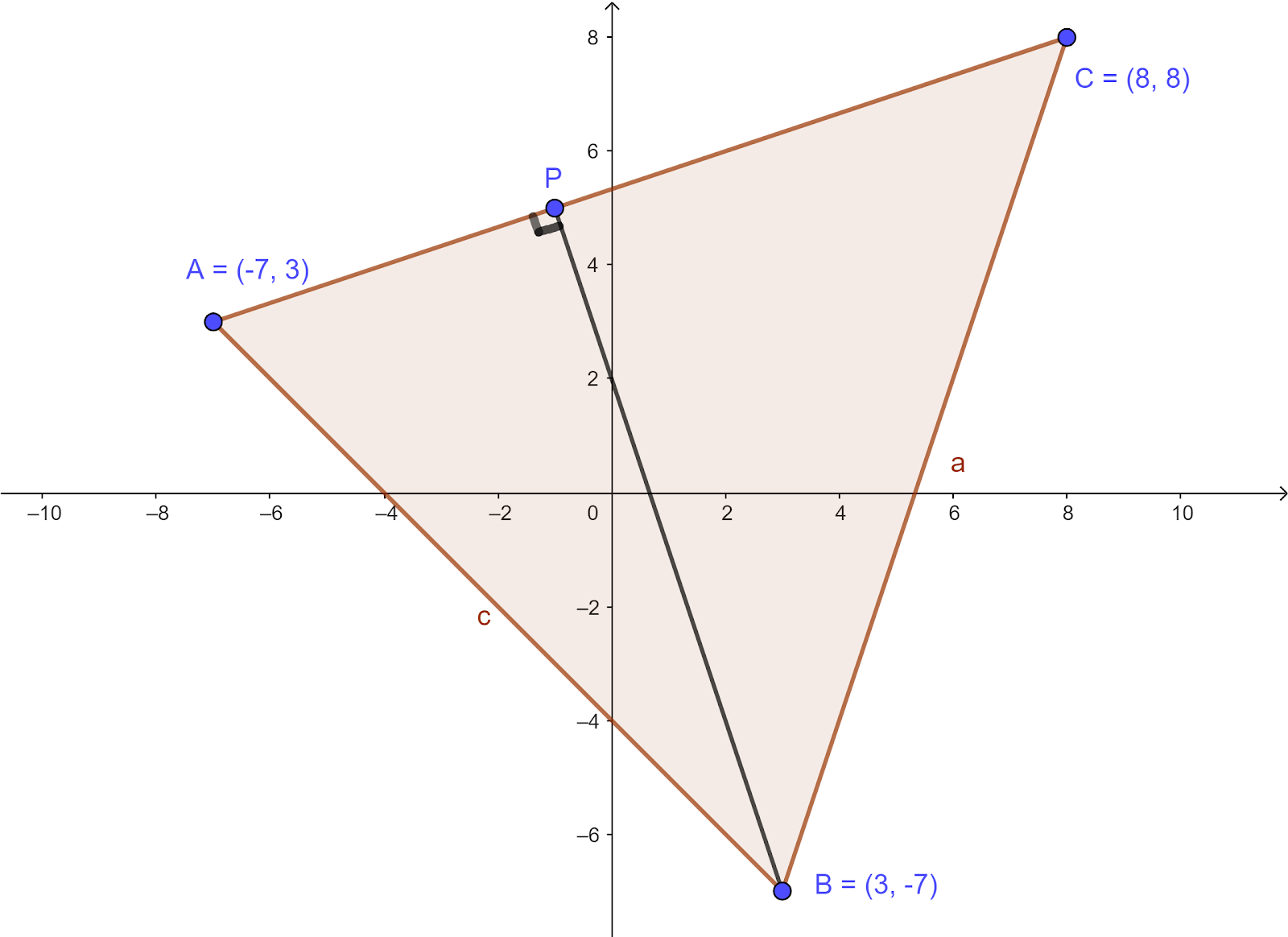
a. Gradient of AC
`frac{8-3}{8-(-7)}=frac{5}{15}=frac{1}{3}`
Equation of BP: `y=mx+c`
`mxxfrac{1}{3}=-1` (as BP is pependicular to AC)
`m=-3`
Substitute point B `(3,-7)` into equation `y=-3x+c`
`-7=-3(3)+c`
`c=2`
Then the equation of BP: `y=-3x+2` (1)
b. As A `(-7,3)` lies on AC using `y-y_1=m(x-x_1)`
`y-3=frac{1}{3}(x-(-7))`
`3y-9=x+7`
`3y=x+16`
`y=frac{x}{3}+frac{16}{3}` (2)
Solve (1) and (2)
Multiply (2) by `9`
`9y=3x+48` (3)
Add (1) and (3)
`10y=50`
`y=5`
Substitute `y=5` into (1)
`5=-3x+2`
`x=-1`
P has coordinates `(-1,5)`
c. The length of AC
`sqrt([8-(-7)]^2+(8-3)^2)=5sqrt10`
The length of BP
`sqrt([(-1)-3]^2+[5-(-7)]^2)=4sqrt10`
d. The area of triangle ABC
`frac{1}{2}xxACxxBP=frac{1}{2}xx5sqrt10xx4sqrt10=100`
Question 4
A circle has radius `10` units and passes through the point `(5, -16)`. The x-axis is a tangent to the circle. Find the possible equations of the circle.
The equation of the circle has radius `10` units
`(x-a)^2+(y-b)^2=(10)^2`
`(x-a)^2+(y-b)^2=100`
The x-axis is a tangent to the circle at a point perpendicular to the radius
`(x-a)^2+[y-(-10])^2=100`
`(x-a)^2+(y+10)^2=100`
Substitute the point `(5, -16)` into the circle
`(5-a)^2+(-16+10)^2=100`
`(5-a)^2+36=100`
`(5-a)^2=64`
`5-a=8` or `5-a=-8`
`a=-3` or `a=13`
Possible equations of the circle
`[x-(-3)]^2+(y+10)^2=100` or `(x-13)^2+(y+10)^2=10`
`(x+3)^2+(y+10)^2=100` or `(x-13)^2+(y+10)^2=10`
Question 5
The line `2y-x=12` intersects the circle `x^2+y^2-10x-12y+36=0` at the points A and B.
a. Find the coordinates of the points A and B.
b. Find the equation of the perpendicular bisector of AB.
c. The perpendicular bisector of AB intersects the circle at the points P and Q. Find the exact coordinates of P and Q.
d. Find the exact area of quadrilateral APBQ.
a. `2y-x=12`
`x=2y-12` (1)
`x^2+y^2-10x-12y+36=0` (2)
Substitute (1) into (2)
`(2y-12)^2+y^2-10(2y-12)-12y+36=0`
`4y^2-48y+144+y^2-20y+120-12y+36=0`
`5y^2-80y+300=0`
`y^2-16y+60=0`
`(y-6)(y-10)=0`
`y-6=0` or `y-10=0`
`y=6` or `y=10`
Substitute `y=6` or `y=10` into (1)
`x=2(6)-12` or `x=2(10)-12`
`x=0` or `x=8`
For two points A and B, one has coordinates `(0,6)` and the other has coordinates `(8,10)`.
b. Gradient of AB
`frac{10-6}{8-0}=frac{4}{8}=frac{1}{2}`
Gradient of the perpendicular bisector `=-2` (as `m_1xxm_2=-1`)
Midpoint of AB
`(frac{0+8}{2},frac{6+10}{2})=(4,8)`
Equation of perpendicular bisector of AB
`y-y_1=m(x-x_1)`
`y-8=-2(x-4)` (as `m=-2`, `x_1=4`, `y_1=8`)
`y-8=-2x+8`
`y=-2x+16` (3)
c. Substitute (3) into (2)
`x^2+(-2x+16)^2-10x-12(-2x+16)+36=0`
`x^2+4x^2-64x+256-10x+24x-192+36=0`
`5x^2-50x+100=0`
`x^2-10x+20=0`
Using quadratic formula `x=frac{-b+-sqrt(b^2-4ac)}{2a}`
`x=frac{-(-10)+-sqrt((-10)^2-4(1)(20))}{2(1)}`
`x=frac{10+-sqrt5}{2}`
`x=5+sqrt5` or `x=5-sqrt5`
Substitute `x=5+sqrt5` or `x=5-sqrt5` into (3)
`y=-2(5+sqrt5)+16` or `y=-2(5-sqrt5)+16`
`y=6-2sqrt5` or `y=6+2sqrt5`
For two points P and Q, one has coordinates `(5+sqrt5,6-2sqrt5)` and the other has coordinates `(5-sqrt5,6+2sqrt5)`.
d. Draw graph
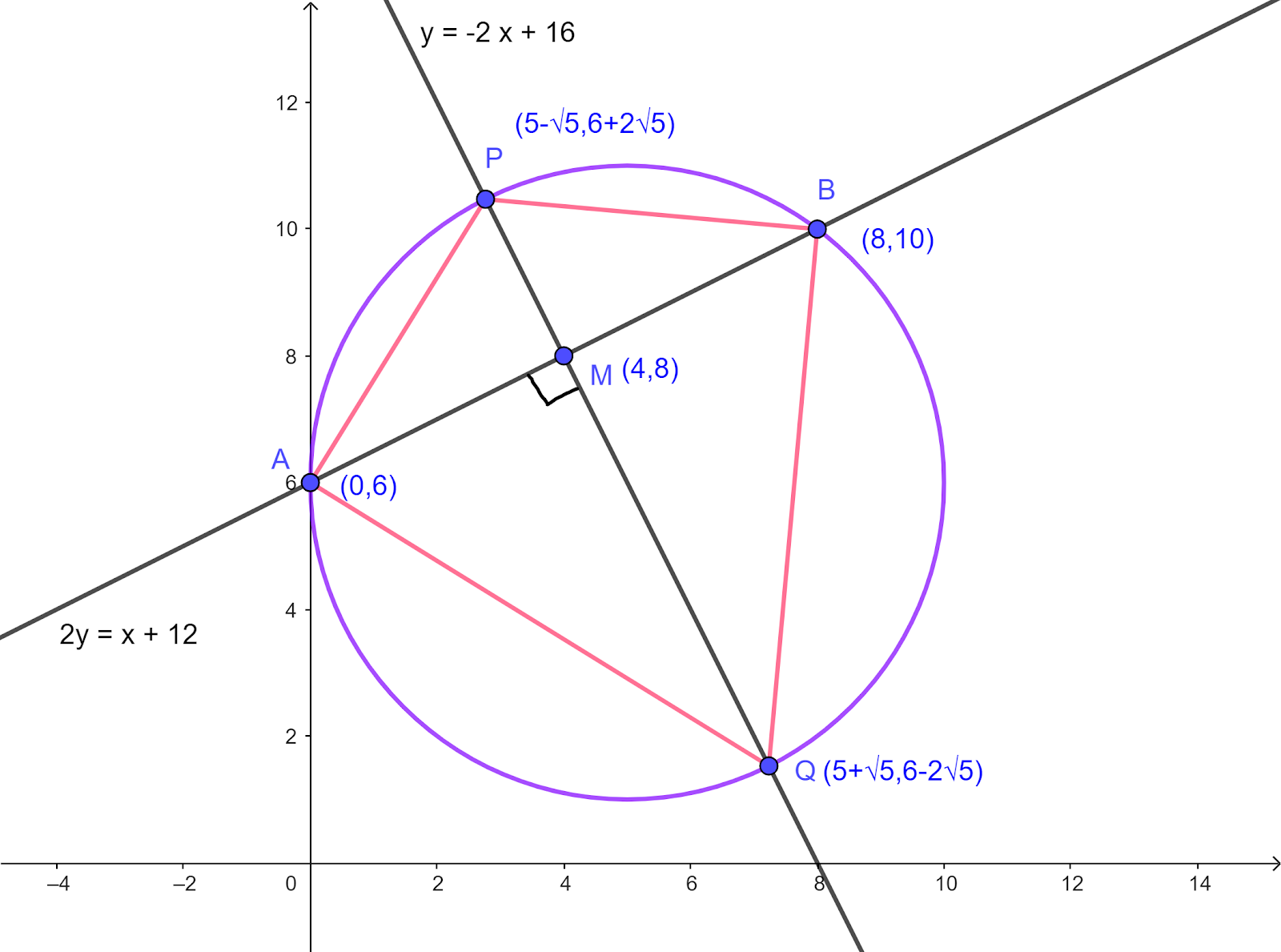
`A=(0,6)`, `B=(8,10)`
The length of AB
`sqrt((8-0)^2+(10-6)^2)=sqrt80`
`P=(5-sqrt5,6+2sqrt5)`, `Q=(5+sqrt5,6-2sqrt5)`
The length of PQ
`sqrt([(5+sqrt5)-(5-sqrt5)]^2+[(6-2sqrt5)-(6+2sqrt5)]^2=10`
APBQ is a cyclic quadrilateral
The area of APBQ `=frac{1}{2}(ABxxPQ)`
`=frac{1}{2}(sqrt80xx10)=20sqrt5`
Question 6
Show that the circles `x^2+y^2=25` and `x^2+y^2-24x-18y` touch each other. Find the coordinates of the point where they touch.
`x^2+y^2=25` (1)
`x^2+y^2-24x-18y+125=0` (2)
Substitute (1) into (2)
`25-24x-18y+125=0`
`24x+18y=150`
`4x+3y=25`
`4x=25-3y`
`x=frac{25-3y}{4}` (3)
Substitute (3) into (1)
`(frac{25-3y}{4})^2+y^2=25`
Multiply by `16`
`(25-3y)^2+16y^2=400`
`625-150y+9y^2+16y^2=400`
`25y^2-150y+225=0`
`y^2-6y+9=0`
`(y-3)^2=0`
`y=3`
As the equation has one repeated root, the line is a tangent at one point of intersection
Substitute `y=3` into (3)
`x=frac{25-3(3)}{4}=4`
The touching point has coordinates `(4,3)`
Substitute (3) into (2)
`(frac{25-3y}{4})^2+y^2-24(frac{25-3y}{4})-18y+125=0`
Multiply by `16`
`(25-3y)^2+16y^2-96(25-3y)-288y+2000=0`
`625-150y+9y^2+16y^2-2400+288y-288y+2000=0`
`25y^2-150y+225=0`
`y^2-6y+9=0`
`(y-3)^2=0`
`y=3`
As the equation has one repeated root, the line is a tangent at one point of intersection
Substitute `y=3` into (3)
`x=frac{25-3(3)}{4}=4`
The touching point has coordinates `(4,3)`
The two circles both touch each other at the point `(4,3)`
Question 7
The curve `y=3sqrt(x-2)` and the line `3x-4y+3=0` intersect at the points P and Q. Find the length of PQ.
For `y=3sqrt(x-2)`
`sqrt(x-2)=frac{y}Ơ3}`
`x-2=(frac{y}[3})^2`
`x=frac{y^2}{9}+2` (1)
`3x-4y+3=0` (2)
Substitute (1) into (2)
`3(frac{y^2}{9}+2)-4y+3=0`
`frac{y^2}{3}+6-4y+3=0`
Multiply by `3`
`y^2+18-12y+9=0`
`y^2-12y+27=0`
`(y-9)(y-3)=0`
`y-9=0` or `y-3=0`
`y=9` or `y=3`
There are two distinct points of intersection P and Q
Substitute `y=9` into (1)
`x=frac{9^2}{9}+2=11`
Substitute `y=3` into (1)
`x=frac{3^2}{9}+2=3`
The intersection points P and Q have coordinates `(11,9)` and `(3,3)`
The length of PQ
`sqrt((3-11)^2+(3-9)^2)=10`
Question 8
The line with gradient `-2` passing through the point P `(3t,2t)` intersects the x-axis at A and the y-axis at B.
a. Find the area of triangle AOB in terms of `t`.
b. The line through P perpendicular to AB intersects the x-axis at C.
Show that the mid-point of PC lies on the line `y=x`.
a. As P `(3t,2t)` lies on the line using `y-y_1=m(x-x_1)`, `m=-2`
`y-2t=-2(x-3t)`
`y-2t=-2x+6t`
`y=-2x+8t`
The line intersects x-axis at A
`0=-2x+8t` (as `y=0`)
`x=4t`
Then `A= (4t,0)`
The line intersects y-axis at B
`y=-2(0)+8t` (as `x=0`)
`y=8t`
Then `B=(0,8t)`
Triangle AOB is right-angled at O (O is the origin)
`AO=4t` and `BO=8t`
The area of triangle AOB
`frac{1}{2}xxAOxxBO=frac{1}{2}xx4txx8t=16t^2` (units2)
b. Gradient of AB
`frac{8t-0}{0-4t}=-2`
Gradient of the line perpendicular to AB `=frac{1}{2}` (as `m_1xxm_2=-1`)
Equation of the line perpendicular to AB
`y-y_1=m(x-x_1)`
`y-2t=frac{1}{2}(x-3t)` (as `m=frac{1}{2}`, `x_1=3t`, `y_1=2t`)
The line intersects x-axis at C
`0-2t=frac{1}{2}(x-3t)` (as `y=0`)
`-4t=x-3t`
`x=-t`
Then C `=(-t,0)`
Midpoint of PC
`(frac{3t+(-t)}{2},frac{2t+0}{2})=(t,t)`
Then the midpoint of PC lies on the line `y=x`
Question 9
The point A has coordinates `(-1,6)` and the point B has coordinates `(7,2)`.
a. Find the equation of the perpendicular bisector of AB, giving your answer in the form `y=mx+c`.
b. A point C on the perpendicular bisector has coordinates (p,q). The distance OC is `2` units, where O is the origin. Write down two equations involving p and q and hence find the coordinates of the possible positions of C.
a. Gradient of AB
`frac{2-6}{7-(-1)}=-frac{1}{2}`
Gradient of the perpendicular bisector `=2` (as `m_1xxm_2=-1`)
Midpoint of AB
`(frac{-1+7}{2},frac{6+2}{2})=(3,4)`
Equation of perpendicular bisector of AB
`y-y_1=m(x-x_1)`
`y-4=2(x-3)` (as `m=2`, `x_1=3`, `y_1=4`)
`y-4=2x-6`
`y=2x-2`
b. The length of OC
`sqrt((p-0)^2+(q-0)^2)=2`
`sqrt(p^2+q^2)=2`
`p^2+q^2=4` (1)
As C (p,q) lies on perpendicular bisector `y=2x-2`
`q=2p-2` (2)
Substitute (2) into (1)
`p^2+(2p-2)^2=4`
`p^2+4p^2-8p+4=4`
`5p^2-8p=0`
`p(5p-8)=0`
`p=0` or `5p-8=0`
`p=0` or `p=frac{8}{5}`
Substitute `p=0` into (2)
`q=2(0)-2=-2`
Substitute `p=frac{8}{5}` into (2)
`q=2(frac{8}{5})-2=frac{6}{5}`
There are two possible positions of C `(0,-2)` and `(frac{8}{5},frac{6}{5})`
Question 10

ABCD is a trapezium with AB parallel to DC and angle BAD `=90°`.
a. Calculate the coordinates of D.
b. Calculate the area of trapezium ABCD.
a. Gradient of AB
`frac{2-17}{3-13}=frac{3}{2}`
Gradient of perpendicular line AD `=-frac{2}{3}` (as `m_1xxm_2=-1`)
Equation of AD
`y-y_1=m(x-x_1)`
`y-17=-frac{2}{3}(x-13)` (as `m=-frac{2}{3}`, `x_1=13`, `y_1=17`)
`y-17=-frac{2}{3}x+frac{26}{3}`
`y=-frac{2}{3}x+frac{77}{3}` (1)
Gradient of DC `=frac{3}{2}` (parallel line to AB)
Equation of DC
`y-y_1=m(x-x_1)`
`y-4=frac{3}{2}(x-13)` (as `m=frac{3}{2}`, `x_1=13`, `y_1=4`)
`y-4=frac{3}{2}x-frac{39}{2}`
`y=frac{3}{2}x-frac{31}{2}` (2)
Point D lies on both line (1) and (2)
`-frac{2}{3}x+frac{77}{3}=frac{3}{2}x-frac{31}{2}`
Multiply by `6`
`-4x+154=9x-93`
`13x=247`
`x=19`
Substitute `x=19` into (2)
`y=frac{3}{2}(19)-frac{31}{2}=13`
Then D has coordinates `(19,13)`
b. The length of AB
`sqrt((13-3)^2+(17-2)^2)=sqrt325`
The length of AD
`sqrt((19-13)^2+(13-17)^2)=sqrt52`
The length of CD
`sqrt((19-13)^2+(13-4)^2)=sqrt117`
The area of trapezium ABCD
`frac{1}{2}xxAD(AB+CD)`
`=frac{1}{2}xxsqrt52(sqrt325+sqrt117)=104`
Question 11
The equation of a circle is `x^2+y^2-8x+4y+4=0`.
a. Find the radius of the circle and the coordinates of its centre.
b. Find the x-coordinates of the points where the circle crosses the x-axis, giving your answers in exact form.
c. Show that the point A `(6,2sqrt3-2)` lies on the circle.
d. Show that the equation of the tangent to the circle at A is `sqrt3x+3y=12sqrt3-6`.
a. `x^2+y^2-8x+4y+4=0`
Write in the form `(x-a)^2+(y-b)^2=r^2`
`x^2-8x+y^2+4y+4=0`
`(x-4)^2-4^2+(y+2)^2-2^2+4=0`
`(x-4)^2+(y+2)^2=16` (1)
The radius is 4, the centre is `(4,-2)`
b. The circle crosses the x-axis
`x^2+(0)^2-8x+4(0)+4=0` (as `y=0`)
`x^2-8x+4=0`
Using quadratic formula `x=frac{-b+-sqrt(b^2-4ac)}{2a}`
`x=frac{-(-8)+-sqrt((-1)^2-4(1)(-1))}{2(1)}`
`x=frac{8+-sqrt48}{2}`
`x=4+2sqrt3` or `x=4-2sqrt3`
c. Substitute `x=6` and `y=2sqrt3-2` into (1)
`(6-4)^2+(2sqrt3-2+2)^2=16`
`2^2+(2sqrt3)^2=16`
`4+12=16`
`16=16` (true)
Then A `(6,2sqrt3-2)` lies on the circle `(x-4)^2+(y+2)^2=16`
d.
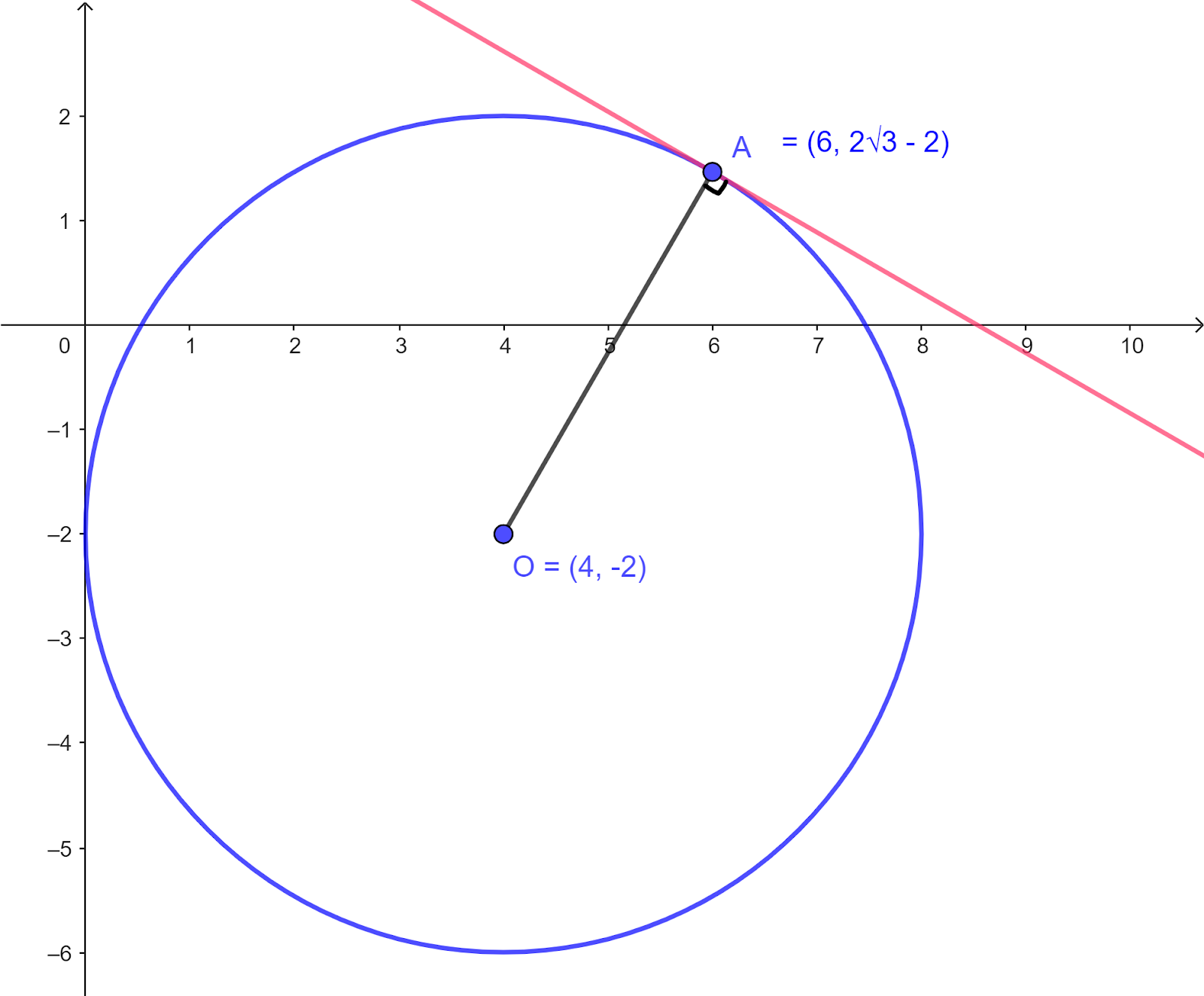
The gradient of OA
`frac{2sqrt3-2-(-2)}{6-4}=frac{2sqrt3}{2}=sqrt3`
The gradient of the tangent at A `=-frac{1}{sqrt3}` (as `m_1xxm_2=-1`)
Equation of the tangent
`y-y_1=m(x-x_1)`
`y-(2sqrt3-2)=-frac{1}{sqrt3}(x-6)` (as `m=-frac{1}{sqrt3}`, `x_1=6`, `y_1=2sqrt3-2`)
Multiply by `sqrt3`
`sqrt3y-(6-2sqrt3)=-1(x-6)`
`sqrt3y-6+2sqrt3=-x+6`
Multiply by `sqrt3`
`3y-6sqrt3+6=-sqrt3x+6sqrt3`
`sqrt3x+3y=12sqrt3-6`
Question 12
Two points A and B have coordinates `(1,3)` and `(9,-1)` respectively. The perpendicular bisector of AB intersects the y-axis at the point C. Find the coordinates of C.
Gradient of AB
`frac{(-1)-3}{9-1}=-frac{4}{8}=-frac{1}{2}`
Gradient of the perpendicular bisector `= 2` (as `m_1xxm_2=-1`)
Midpoint of AB
`(frac{1+9}{2},frac{3+(-1)}{2})=(5,1)`
Equation of perpendicular bisector of AB
`y-y_1=m(x-x_1)`
`y-1=2(x-5)` (as `m=2`, `x_1=5`, `y_1=1`)
`y-1=2x-10`
`y=2x-9`
The perpendicular bisector intersects y-axis at C
`y=2(0)-9` (as `x=0`)
`y=-9`
Then C `=(0,-9)`
Question 13
The diagram shows a trapezium ABCD in which the coordinates of A, B and C are `(4,0)`, `(0,2)` and `(h,3h)` respectively. The lines BC and AD are parallel, angle ABC `=90°` and CD is parallel to the x-axis.
a. Find, by calculation, the value of h.
b. Hence find the coordinates of D.
a. Gradient of AB
`frac{2-0}{0-4}=-frac{2}[4}=-frac{1}{2}`
Gradient of BC
`frac{3h-2}{h-0}=frac{3h-2}{h}`
For `m_1xxm_2=-1`
`frac{3h-2}{h}xx(-frac{1}{2})=-1`
`frac{3h-2}{h}=2`
`3h-2=2h`
`h=2`
Then C `=(2,6)`
b. D `=(x,6)` (as y coordinate of D is `6`, CD parallel to the x-axis)
Gradient of AD `=2` (parallel line to BC)
`frac{6-0}{x-4}=2`
`6=2(x-4)`
`6=2x-8`
`x=7`
Then D `=(7,6)`
Question 14
The equation of a circle with centre C is `x^2+y^2-8x+4y-5=0`.
a. Find the radius of the circle and the coordinates of C.
b. The point P `(1,2)` lies on the circle. Show that the equation of the tangent to the circle at P is `4y=3x+5`.
c. The point Q also lies on the circle and PQ is parallel to the x-axis. Write down the coordinates of Q.
d. The tangents to the circle at P and Q meet at T. Find the coordinates of T.
a. The equation of the circle
`(x-a)^2+(y-b)^2=r^2`
`x^2+y^2-2ax-2by+a^2+b^2-r^2=0`
For `x^2+y^2-8x+4y-5=0`
`-2ax=-8x` and `-2by=4y` and `a^2+b^2-r^2=-5`
`a=4` and `b=-2` and `(4)^2+(-2)^2-r^2=-5`
`a=4` and `b=-2` and `r=5`
The centre C has coordinates `4,-2)`
Radius `= 5`
b. Gradient of PC
`frac{(-2)-2}{4-1}=-frac{4}{3}`
Gradient of the tangent at P `=frac{3}{4}` (as `m_1xxm_2=-1`)
Equation of the tangent
`y-y_1=m(x-x_1)`
`y-2=frac{3}{4}(x-1)` (as `m=frac{3}{4}`, `x_1=1`, `y_1=2`)
`4y-8=3x-3`
`4y=3x+5`
c.
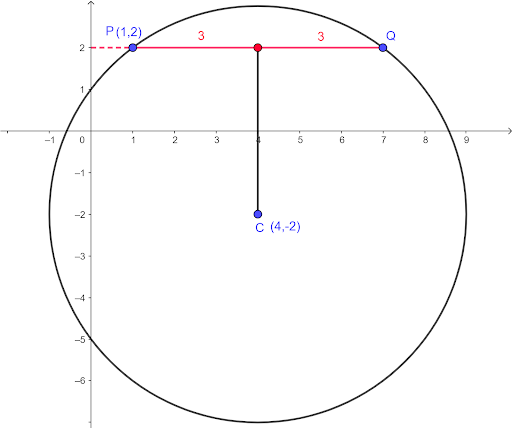
Gradient of PQ `= 0` (parallel to the x-axis)
Q `= (x,2)` (as y coordinate of D is `2`)
The x coordinate of the point Q
`1+3+3=7`
Then Q `= (7,2)`
d.
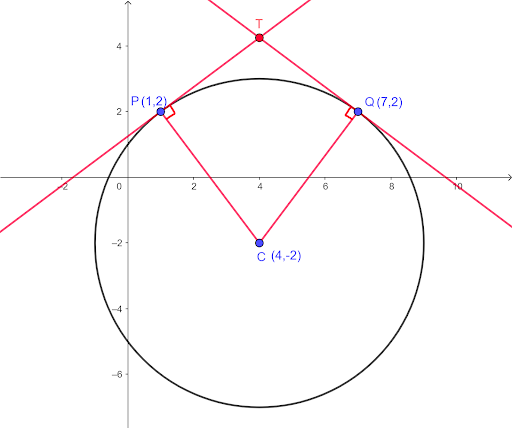
Gradient of PT `=frac{3}{4}` (part b)
Equation of the tangent PT
`4y=3x+5` (1)
Gradient of CQ
`frac{2-(-2)}{7-4}=frac{4}{3}`
Gradient of QT `=-frac{3}{4}` (as `m_1xxm_2=-1`)
Equation of the tangent PT
`y-y_1=m(x-x_1)`
`y-2=-frac{3}{4}(x-7)` (as `m=-frac{3}{4}`, `x_1=7`, `y_1=2`)
`4y-8=-3x+21`
`4y=-3x+29` (2)
Point T lies on both two tangent (1) and (2)
`3x+5=-3x+29`
`6x=24`
`x=4`
Substitute `x=4` into (1)
`4y=3(4)+5`
`4y=17`
`y=frac{17}{4]`
Then T `=(4,frac{17}{4])`
Question 15

The diagram shows a circle with centre A passing through the point B. A second circle has centre B and passes through A. The tangent at B to the first circle intersects the second circle at C and D.
The coordinates of A are `(-1,4)` and the coordinates of B are `(3,2)`.
a. Find the equation of the tangent CBD.
b. Find an equation of the circle with centre B.
c. Find, by calculation, the x-coordinates of C and D.
a. The gradient of AB
`frac{2-4}{3-(-1)}=-frac{2}{4}=-frac{1}{2}`
Gradient of the tangent `= 2` (as `m_1xxm_2=-1`)
Equation of the tangent CBD
`y-y_1=m(x-x_1)`
`y-2=2(x-3)` (as `m=2`, `x_1=3`, `y_1=2`)
`y=2x-4` (1)
b. The length of AB as well as the radius
`sqrt((3-(-1))^2+(2-4)^2)=sqrt20`
Equation of the circle centre B
`(x-a)^2+(y-b)^2=r^2`
`(x-3)^2+(y-2)^2=20` (as `a=3`, `b=2`, `r=sqrt20`) (2)
c. Substitute (1) into (2)
`(x-3)^2+(2x-4-2)^2=20`
`x^2-6x+9+4x^2-24x+36=0`
`5x^2-30x+25=0`
`5(x-5)(x-1)=0`
`x-5=0` or `x-1=0`
`x=5` or `x=1`
The intersection points C and D have the x-coordinates `5` and `1`
Question 16
The line `y=2x+5` intersects the circle with equation `x^2+y^2=20` at A and B.
a. Find the coordinates of A and B in surd form and hence find the exact length of the chord AB.
b. A straight line through the point `(10,0)` with gradient m is a tangent to the circle. Find the two possible values of m.
a. `y=2x+5` (1)
`x^2+y^2=20` (2)
Substitute (1) into (2)
`x^2+(2x+5)^2=20`
`x^2+4x^2+20x+25=20`
`5x^2+20x+5=0`
`5(x^2+4x+1)=0`
Using quadratic formula `x=frac{-b+-sqrt(b^2-4ac)}{2a}`
`x=frac{-4+-sqrt((4)^2-4(1)(1))}{2(1)}`
`x=frac{-4+-sqrt12}{2}`
`x=-2+sqrt3` or `x=-2-sqrt3`
Substitute `x=-2+sqrt3` or `x=-2-sqrt3` into (1)
`y=2(-2+sqrt3)+5` or `y=2(-2-sqrt3)+5`
`y=1+2sqrt3` or `y=1-2sqrt3`
The intersection points A and B have coordinates `(-2+sqrt3,1+2sqrt3)` and `(-2-sqrt3,1-2sqrt3)`
The length of AB
`sqrt([(-2-sqrt3)-(-2+sqrt3)]^2+[(1-2sqrt3)-(1+2sqrt3)]^2)=sqrt60`
Equation of the tangent
`y-y_1=m(x-x_1)`
`y-0=m(x-10)` (as `x_1=10`, `y_1=0`)
`y=mx-10m` (3)
Substitute (3) into (2)
`x^2+(mx-10m)^2=20`
`x^2+m^2x^2-20m^2x+100m^2-20=0`
`(1+m^2)x^2-20m^2x+20(5m^2-1)=0`
Using formula `b^2-4ac=0`
`(-20m^2)^2-80(1+m^2)(5m^2-1)=0`
`400m^4-80(5m^2-1+5m^4-m^2)=0`
`400m^4-400m^2+80-400m^4+80m^2=0`
`-320m^2=-80`
`m^2=frac{1}{4}`
`m=frac{1}{2}` or `m=-frac{1}{2}`
Question 17
a. A circle with centre `(5,2)` passes through the point `(7,5)`. Find an equation of the circle.
b. The line intersects the circle at A and B. Find the exact length of the chord AB.
a. The equation of the circle
`(x-a)^2+(y-b)^2=r^2`
`(7-5)^2+(5-2)^2=r^2`
`13=r^2`
Then `(x-5)^2+(y-2)^2=13` (1)
b. `y=5x-10` (2)
Substitute (2) into (1)
`(x-5)^2+(5x-10-2)^2=13`
`x^2-10x+25+25x^2-120x+144-13=0`
`26x^2-130x+156=0`
`26(x^2-5x+6)=0`
`26(x-3)(x-2)=0`
`x-3=0` or `x-2=0`
`x=3` or `x=2`
Substitute `x=3` or `x=2` into (2)
`y=5(3)-10` or `y=5(2)-10`
`y=5` or `y=0`
The intersection points A and B have coordinates `(3,5)` and `(2,0)`
The length of AB
`sqrt((2-3)^2+(0-5)^2)=sqrt26`
Question 18
A line has equation `y=3x+k` and a curve has equation `y=x^2+kx+6`, where k is a constant.
Find the set of values of k for which the line and curve have two distinct points of intersection.
The line intersects the curve at two distinct points
`3x+k=x^2+kx+6`
`x^2+(k-3)x+6-k=0`
Using formula `b^2-4ac>0`
`(k-3)^2-4(1)(6-k)>0`
`k^2-6k+9-24+4k>0`
`k^2-2k-15>0`
`(k+3)(k-5)>0`
`k+3>0` or `k-5>0`
`k<-3` or `k>5`
Question 19
The equation of a circle is `x^2+y^2+ax+by-12=0`. The points A `(1,1)` and B `(2,-6)` lie on the circle.
a. Find the values of a and b and hence find the coordinates of the centre of the circle.
b. Find the equation of the tangent to the circle at the point A, giving your answer in the form `px+qy=k`, where p, q and k are integers.
a. `x^2+y^2+ax+by-12=0` (1)
Substitute point A `(1,1)` into (1)
`(1)^2+(1)^2+a(1)+b(1)-12=0`
`a=10-b` (2)
Substitute point B `(2,-6)` into (1)
`(2)^2+(-6)^2+a(2)+b(-6)-12=0`
`2a-6b=-28` (3)
Substitute (2) into (3)
`2(10-b)-6b=-28`
`20-2b-6b=-28`
`8b=48`
`b=6`
Substitute `b=6` into (2)
`a=10-6=4`
Equation of the circle centre C (a,b)
`(x-a)^2+(y-b)^2=r^2`
Substitute `a=4` and `b=6` into (1)
`x^2+y^2+4x+6y-12=0`
`x^2+4x+2^2-2^2+y^2+6y+3^2-3^2-12=0`
`(x+2)^2+(y+3)^2-4-9-12=0`
`(x+2)^2+(y+3)^2=25`
Then the centre C has the coordinates `(-2,-3)`
b. The gradient of AC
`frac{-3-1}{-2-1}=frac{4}{3}`
Gradient of the tangent `=-frac{3}{4}` (as `m_1xxm_2=-1`)
Equation of the tangent
`y-y_1=m(x-x_1)`
`y-1=-frac{3}{4}(x-1)` (as `m=-frac{3}{4}`, `x_1=1`, `y_1=1`)
`4y-4=-3x+3`
`3x+4y=7`
Question 20
The equation of a circle is `(x-a)^2+(y-3)^2=20`. The line `y=frac{1}{2}x+6` is a tangent to the circle at the point P.
a. Show that one possible value of a is 4 and find the other possible value.
b. For a `= 4`, find the equation of the normal to the circle at P.
c. For a `= 4`, find the equations of the two tangents to the circle which are parallel to the normal found in (b).
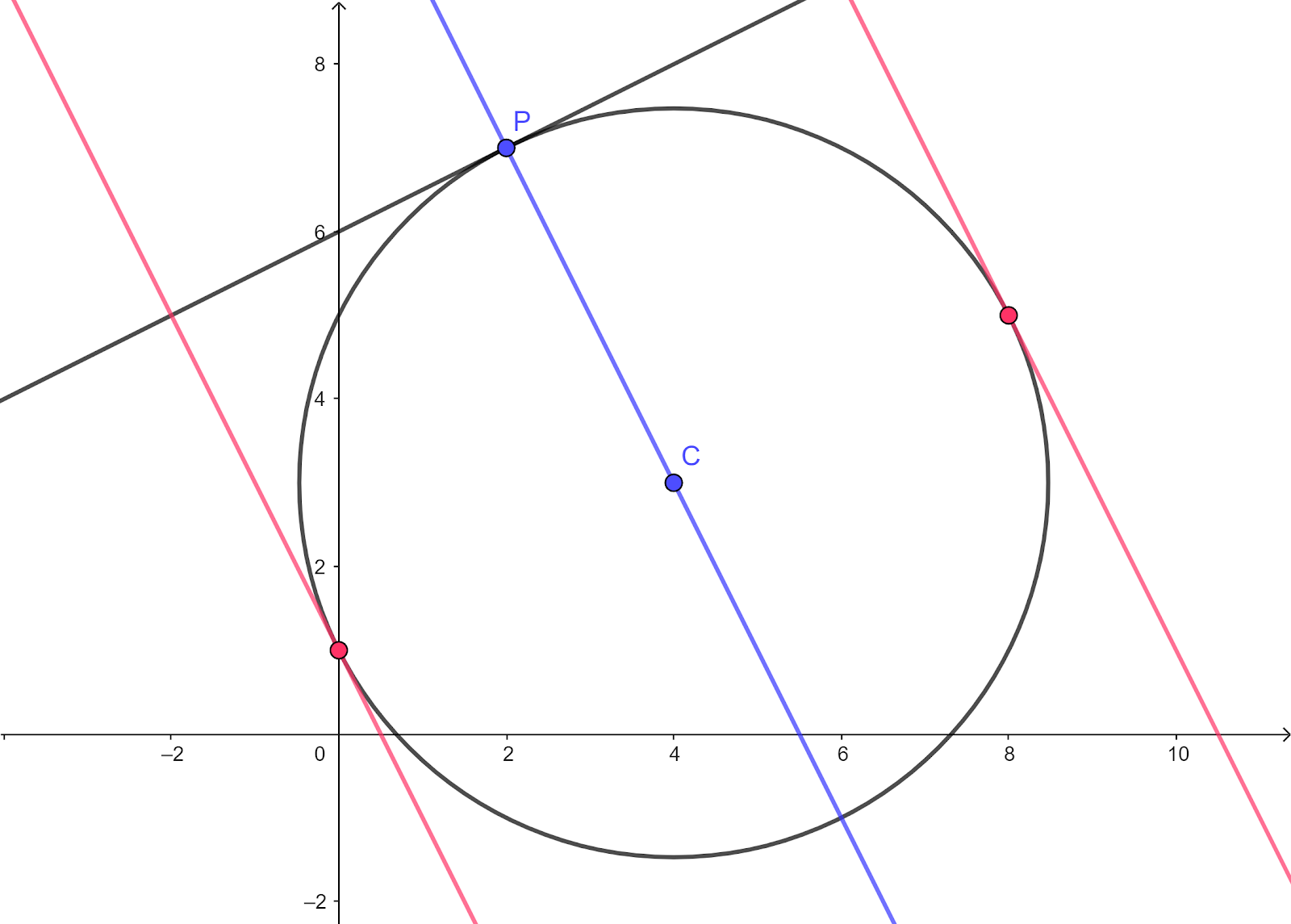
a. `(x-a)^2+(y-3)^2=20` (1)
`y=frac{1}{2}x+6` (2)
Substitute (2) to (1)
`(x-a)^2+(frac{1}{2}x+6-3)^2=20`
`(x-a)^2+(frac{1}{2}x+3)^2=20`
`x^2-2ax+a^2+frac{1}{4}x^2+3x+9-20=0`
`frac{5}{4}x^2+(3-2a)x+a^2-11=0` (3)
Using formula `b^2-4ac=0`
`(3-2a)^2-4(frac{5}{4})(a^2-11)=0`
`9-12a+4a^2-5a^2+55=0`
`-a^2-12a+64=0`
`a^2+12a-64=0`
`(a-4)(a+16)=0`
`a=4` or `a=-16`
b. Substitute `a = 4` into (3)
`frac{5}{4}x^2+(3-2(4))x+(4)^2-11=0`
`frac{5}{4}x^2-5x+5=0`
Multiply by `frac{4}{5}`
`x^2-4x+4=0`
`(x-2)(x-2)=0`
`x=2`
Substitute into `x=2` (2)
`y=frac{1}{2}(2)+6=7`
Then P `=(2,7)`
Gradient of the normal
`m_"tangent"xxm_"normal"=-1`
`frac{1}{2}xxm_"normal"=-1`
`m_"normal"=-2`
Equation of the normal
`y-y_1=m(x-x_1)`
`y-7=-2(x-2)` (as `m=-2`, `x_1=2`, `y_1=7`)
`y-7=-2x+4`
`y=-2x+11`
c. Substitute `a = 4` into (1)
`(x-4)^2+(y-3)^2=20` (3)
Then the centre C has the coordinates `(4,3)`
Gradient of the two tangents `=frac{1}{2}`
Equation of the diameter
`y-y_1=m(x-x_1)`
`y-3=frac{1}{2}(x-4)` (as `m=1/2`, `x_1=4`, `y_1=3`)
`y=1/2x+1` (4)
Substitute (4) into (3)
`(x-4)^2+(1/2x+1-3)^2=20`
`(x-4)^2+(1/2x-2)^2=20`
`x^2-8x+16+1/4x^2-2x+4-20=0`
`5/4x^2-10x=0`
`x(5/4x-10)=0`
`x=0` or `x=8`
Substitute `x=0` or `x=8` into (4)
`y=1/2(0)+1` or `y=1/2(8)+1`
`y=1` or `y=5`
Equation of the first tangent
`y-1=-2(x-0)` (as `m=-2`, `x_1=0`, `y_1=1`)
`y=-2x+1`
Equation of the second tangent
`y-5=-2(x-8)` (as `m=-2`, `x_1=8`, `y_1=5`)
`y=-2x+21`
Question 1
In triangle ABC, the midpoints of the sides AB, BC and AC are `(1,4)`, `(2,0)` and `(-4,1)`, respectively. Find the coordinates of points A, B and C.
Question 2
Three points have coordinates A `(7,4)`, B `(19,8)` and C `(k,2k)`. Find the value of the constant `k` for which:
a. C lies on the line that passes through the points A and B
b. angle CAB is `90°`
Question 3
The coordinates of triangle ABC are A `(-7,3)`, B `(3,-7)` and C `(8,8)`. P is the foot of the perpendicular from B to AC.
a. Find the equation of the line BP.
b. Find the coordinates of P.
c. Find the lengths of AC and BP.
d. Use your answers to part c to find the area of triangle ABC.
Question 4
A circle has radius `10` units and passes through the point `(5, -16)`. The x-axis is a tangent to the circle. Find the possible equations of the circle.
Question 5
The line `2y-x=12` intersects the circle `x^2+y^2-10x-12y+36=0` at the points A and B.
a. Find the coordinates of the points A and B.
b. Find the equation of the perpendicular bisector of AB.
c. The perpendicular bisector of AB intersects the circle at the points P and Q. Find the exact coordinates of P and Q.
d. Find the exact area of quadrilateral APBQ.
Question 6
Show that the circles `x^2+y^2=25` and `x^2+y^2-24x-18y` touch each other. Find the coordinates of the point where they touch.
Question 7
The curve `y=3sqrt(x-2)` and the line `3x-4y+3=0` intersect at the points P and Q. Find the length of PQ.
Question 8
The line with gradient `-2` passing through the point P `(3t,2t)` intersects the x-axis at A and the y-axis at B.
a. Find the area of triangle AOB in terms of `t`.
b. The line through P perpendicular to AB intersects the x-axis at C.
Show that the mid-point of PC lies on the line `y=x`.
Question 9
The point A has coordinates `(-1,6)` and the point B has coordinates `(7,2)`.
a. Find the equation of the perpendicular bisector of AB, giving your answer in the form `y=mx+c`.
b. A point C on the perpendicular bisector has coordinates (p,q). The distance OC is `2` units, where O is the origin. Write down two equations involving p and q and hence find the coordinates of the possible positions of C.
Question 10

ABCD is a trapezium with AB parallel to DC and angle BAD `=90°`.
a. Calculate the coordinates of D.
b. Calculate the area of trapezium ABCD.
Question 11
The equation of a circle is `x^2+y^2-8x+4y+4=0`.
a. Find the radius of the circle and the coordinates of its centre.
b. Find the x-coordinates of the points where the circle crosses the x-axis, giving your answers in exact form.
c. Show that the point A `(6,2sqrt3-2)` lies on the circle.
d. Show that the equation of the tangent to the circle at A is `sqrt3x+3y=12sqrt3-6`.
Question 12
Two points A and B have coordinates `(1,3)` and `(9,-1)` respectively. The perpendicular bisector of AB intersects the y-axis at the point C. Find the coordinates of C.
Question 13
The diagram shows a trapezium ABCD in which the coordinates of A, B and C are `(4,0)`, `(0,2)` and `(h,3h)` respectively. The lines BC and AD are parallel, angle ABC `=90°` and CD is parallel to the x-axis.
a. Find, by calculation, the value of h.
b. Hence find the coordinates of D.
Question 14
The equation of a circle with centre C is `x^2+y^2-8x+4y-5=0`.
a. Find the radius of the circle and the coordinates of C.
b. The point P `(1,2)` lies on the circle. Show that the equation of the tangent to the circle at P is `4y=3x+5`.
c. The point Q also lies on the circle and PQ is parallel to the x-axis. Write down the coordinates of Q.
d. The tangents to the circle at P and Q meet at T. Find the coordinates of T.
Question 15

The diagram shows a circle with centre A passing through the point B. A second circle has centre B and passes through A. The tangent at B to the first circle intersects the second circle at C and D.
The coordinates of A are `(-1,4)` and the coordinates of B are `(3,2)`.
a. Find the equation of the tangent CBD.
b. Find an equation of the circle with centre B.
c. Find, by calculation, the x-coordinates of C and D.
Question 16
The line `y=2x+5` intersects the circle with equation `x^2+y^2=20` at A and B.
a. Find the coordinates of A and B in surd form and hence find the exact length of the chord AB.
b. A straight line through the point `(10,0)` with gradient m is a tangent to the circle. Find the two possible values of m.
Question 17
a. A circle with centre `(5,2)` passes through the point `(7,5)`. Find an equation of the circle.
b. The line intersects the circle at A and B. Find the exact length of the chord AB.
Question 18
A line has equation `y=3x+k` and a curve has equation `y=x^2+kx+6`, where k is a constant.
Find the set of values of k for which the line and curve have two distinct points of intersection.
Question 19
The equation of a circle is `x^2+y^2+ax+by-12=0`. The points A `(1,1)` and B `(2,-6)` lie on the circle.
a. Find the values of a and b and hence find the coordinates of the centre of the circle.
b. Find the equation of the tangent to the circle at the point A, giving your answer in the form `px+qy=k`, where p, q and k are integers.
Question 20
The equation of a circle is `(x-a)^2+(y-3)^2=20`. The line `y=frac{1}{2}x+6` is a tangent to the circle at the point P.
a. Show that one possible value of a is 4 and find the other possible value.
b. For a `= 4`, find the equation of the normal to the circle at P.
c. For a `= 4`, find the equations of the two tangents to the circle which are parallel to the normal found in (b).