A Level Mathematics - Questionbank
Circular measure focuses on the radian as a unit of angle measurement and its applications in solving problems involving arcs and sectors of circles. Students learn to calculate arc lengths, areas of sectors, and segments using radian measure. This topic is fundamental for understanding trigonometry and its applications in geometry and calculus.
Question 1
Calculate the length of BC
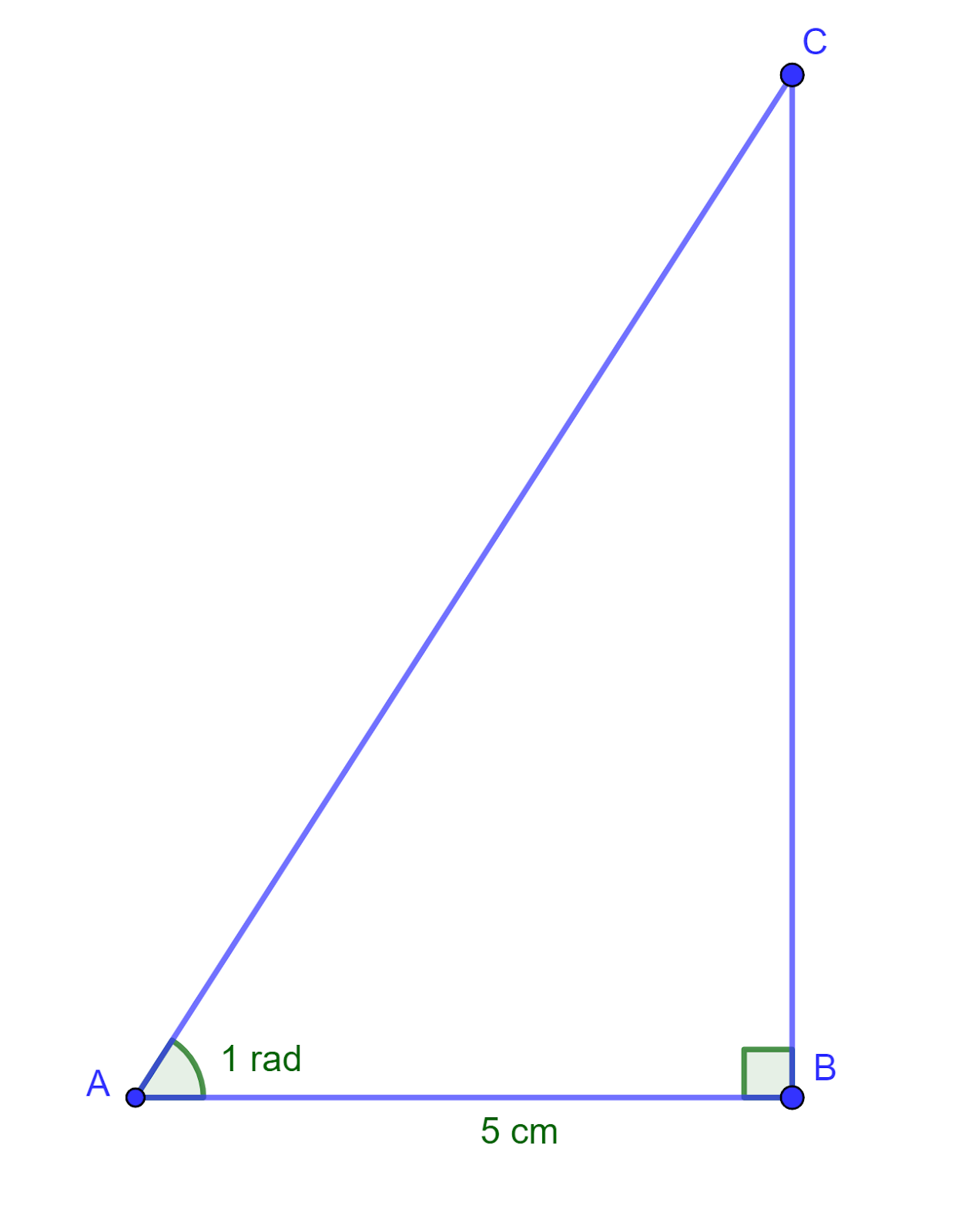
Easy
Mark as Complete
Mark Scheme
Question 2
Find, in terms of `pi`, the arc length of a sector of:
a. radius `8` cm and angle `pi/4`
b. radius `7` cm and angle `frac{3pi}{7}`
Easy
Mark as Complete
Mark Scheme
Question 3
Find the arc length of a sector of
a. radius `10` cm and angle `1.3` radians.
b. radius `3.5` cm and angle `0.65` radians.
Easy
Mark as Complete
Mark Scheme
Question 4
Find, in radians, the angle of a sector of:
a. radius `10` cm and arc length `5` cm
b. radius `12` cm and arc length `9.6` cm
Easy
Mark as Complete
Mark Scheme
Question 5
The High Roller Ferris wheel in the USA has a diameter of `158.5` metres. Calculate the distance travelled by a capsule as the wheel rotates through `pi/16` radians.
Easy
Mark as Complete
Mark Scheme
Question 6
Find the perimeter of each of these sectors.
a.
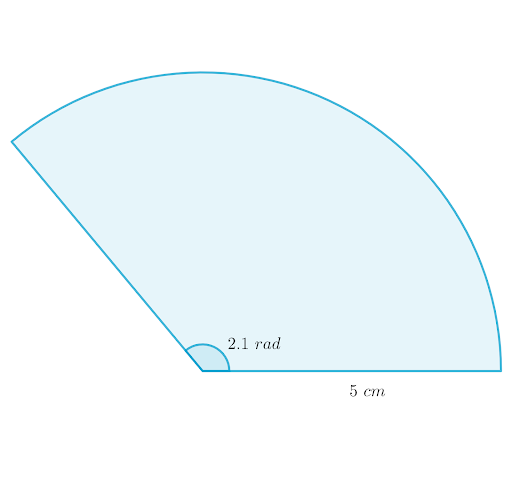
b.
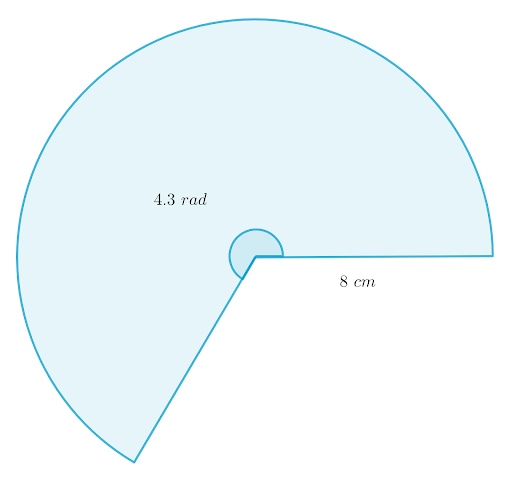
Easy
Mark as Complete
Mark Scheme
Question 7
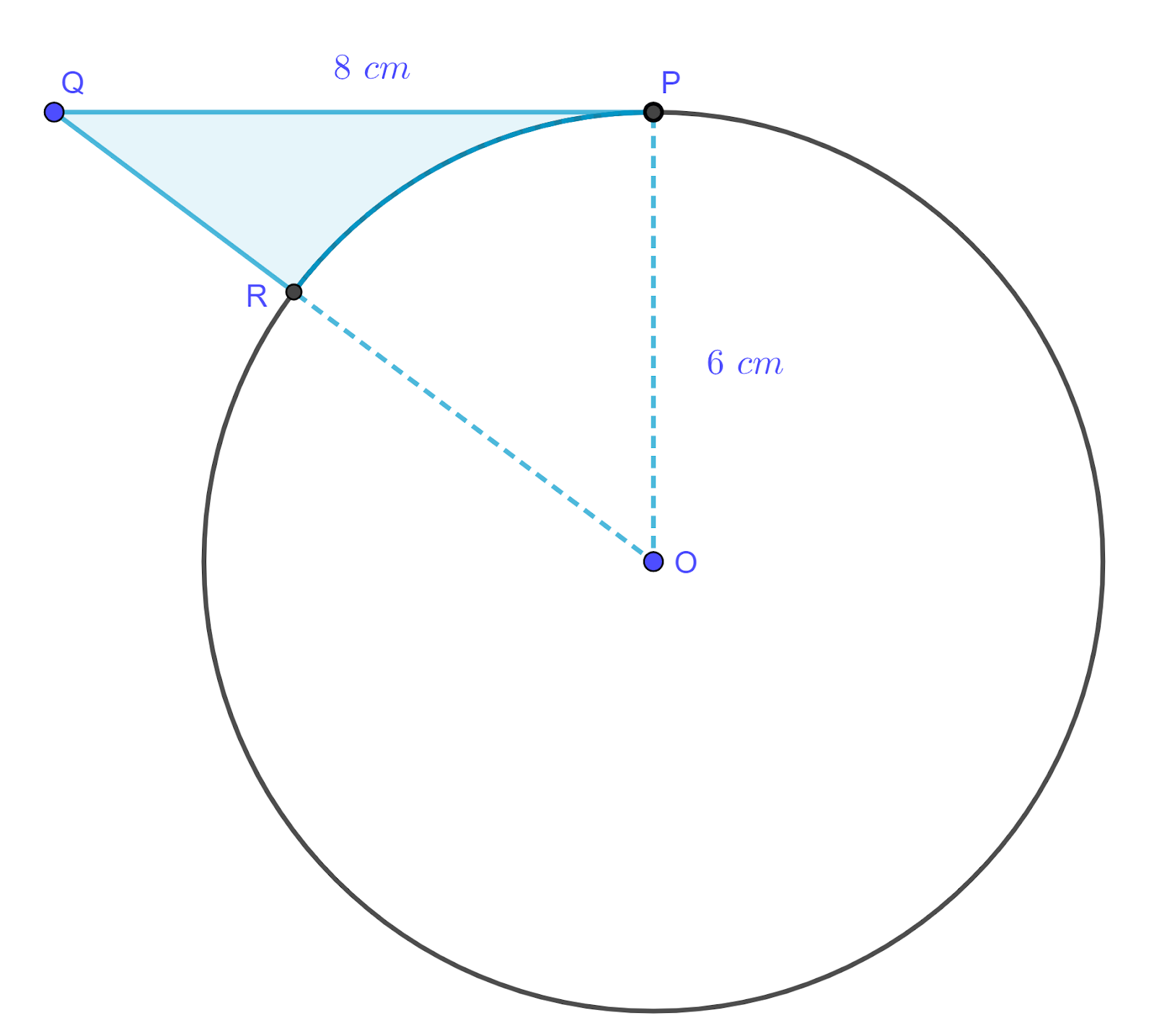
The circle has radius 6 cm and centre O. PQ is a tangent to the circle at the point P. QRO is a straight line. Find:
a. angle POQ, in radians
b. the length of QR
c. the perimeter of the shaded area
Medium
Mark as Complete
Mark Scheme
Question 8
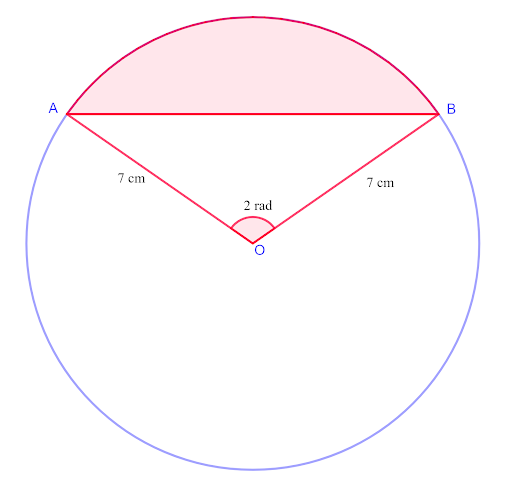
The circle has radius `7` cm and centre O. AB is a chord and angle AOB `=2` radians. Find:
a. the length of arc AB
b. the length of chord AB
c. the perimeter of the shaded segment
Medium
Mark as Complete
Mark Scheme
Question 9
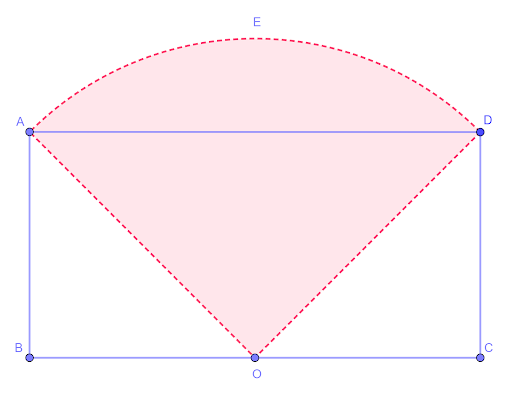
ABCD is a rectangle with AB `= 5` cm and BC `= 24` cm. O is the midpoint of BC. OAED is a sector of a circle, centre O. Find:
a. the length of AO
b. angle AOD, in radians
c. the perimeter of the shaded region
Medium
Mark as Complete
Mark Scheme
Question 10
Find, in terms of `pi`, the area of a sector of:
a. radius `10` cm and angle `frac{2pi}{5}` radians
b. radius `4.5` cm and angle `frac{2pi}{9}` radians
Easy
Mark as Complete
Mark Scheme
Question 11
AOB is a sector of a circle, centre O, with radius `8` cm. The length of arc AB is `10` cm. Find:
a. angle AOB, in radians
b. the area of the sector AOB
Easy
Mark as Complete
Mark Scheme
Question 12
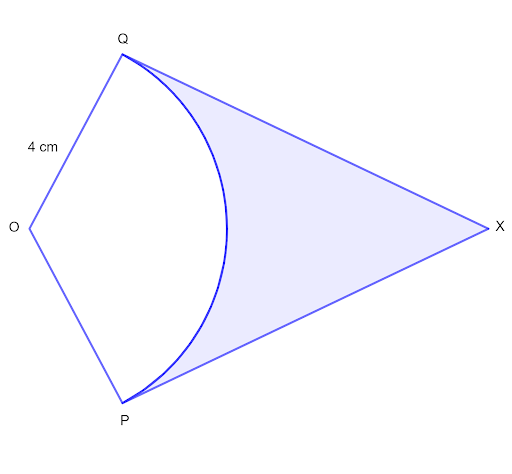
The diagram shows a sector, POQ, of a circle, centre O, with radius `4` cm. The length of arc PQ is `7` cm. The lines PX and QX are tangents to the circle at P and Q, respectively.
a. Find angle POQ, in radians
b. Find the length of PX
c. Find the area of the shaded region.
Hard
Mark as Complete
Mark Scheme
Question 13
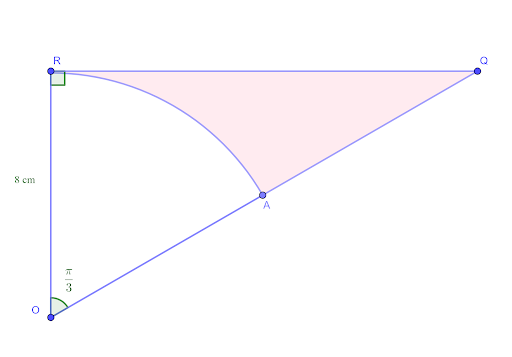
The diagram shows a sector, POR, of a circle, centre O, with radius `8` cm and sector angle `pi/3` radians. The lines OR and QR are perpendicular and OPQ is a straight line.
Find the exact area of the shaded region.
Medium
Mark as Complete
Mark Scheme
Question 14
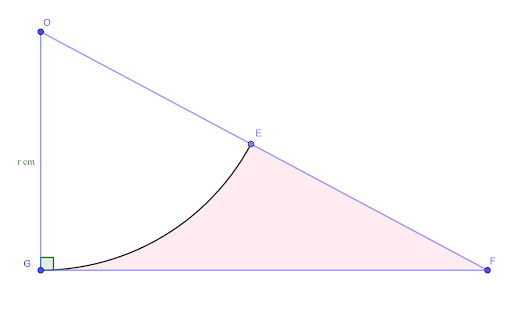
The diagram shows a sector, EOG, of a circle, centre O, with radius `r` cm. The line GF is a tangent to the circle at G, and E is the midpoint of OF.
a. The perimeter of the shaded region is `P` cm. Show that `P=r/3(3+3sqrt3+pi)`
b. The area of the shaded region is `A` cm2. Show that `A=r^2/6(3sqrt3-pi)`
Hard
Mark as Complete
Mark Scheme
Question 15
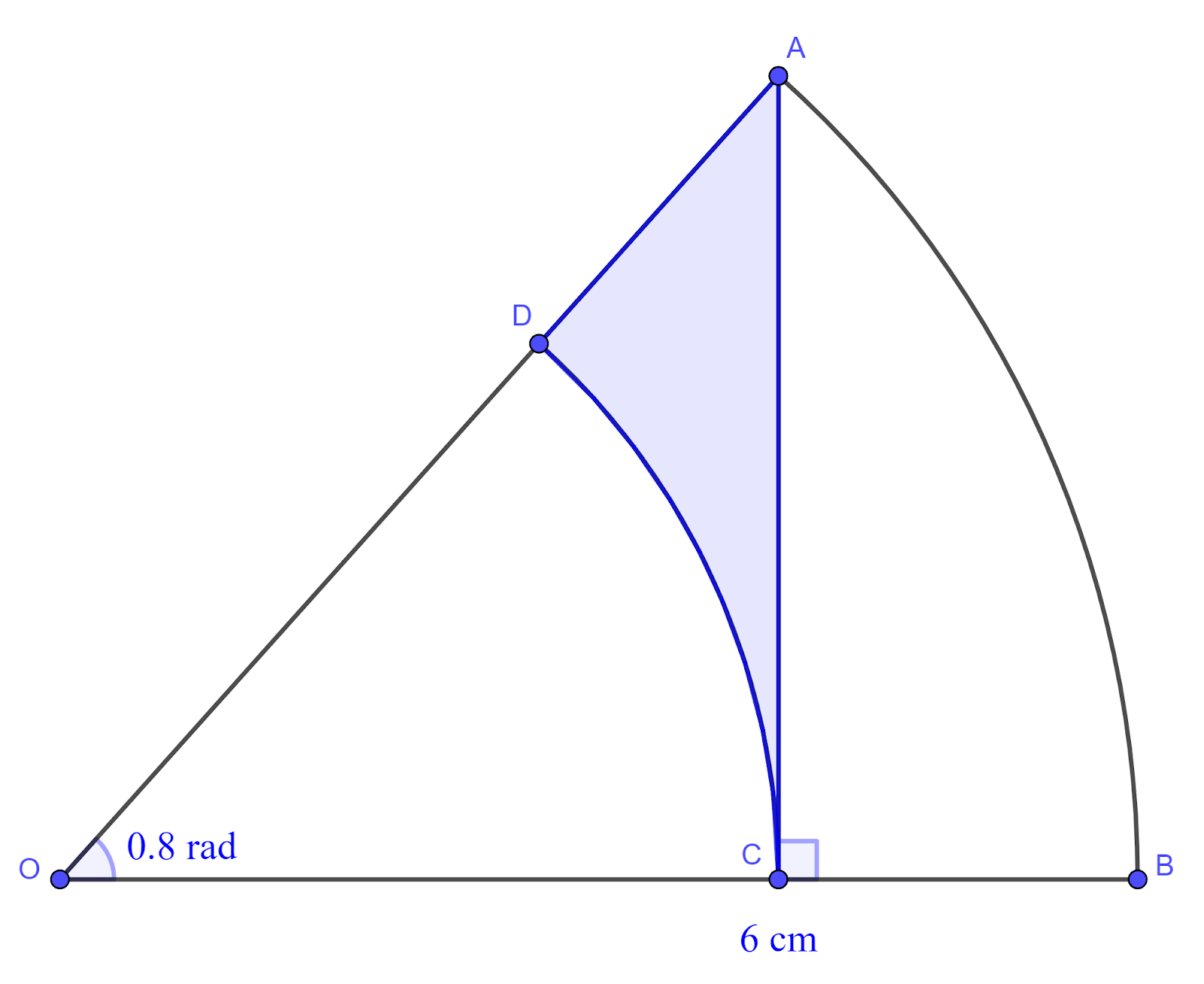
The diagram shows a sector AOB which is part of a circle with centre O and radius `6` cm and with angle AOB `=0.8` radians. The point C on OB is such that AC is perpendicular to OB. The arc CD is part of a circle with centre O, where D lies on OA.
Find the area of the shaded region.
Medium
Mark as Complete
Mark Scheme
Question 16
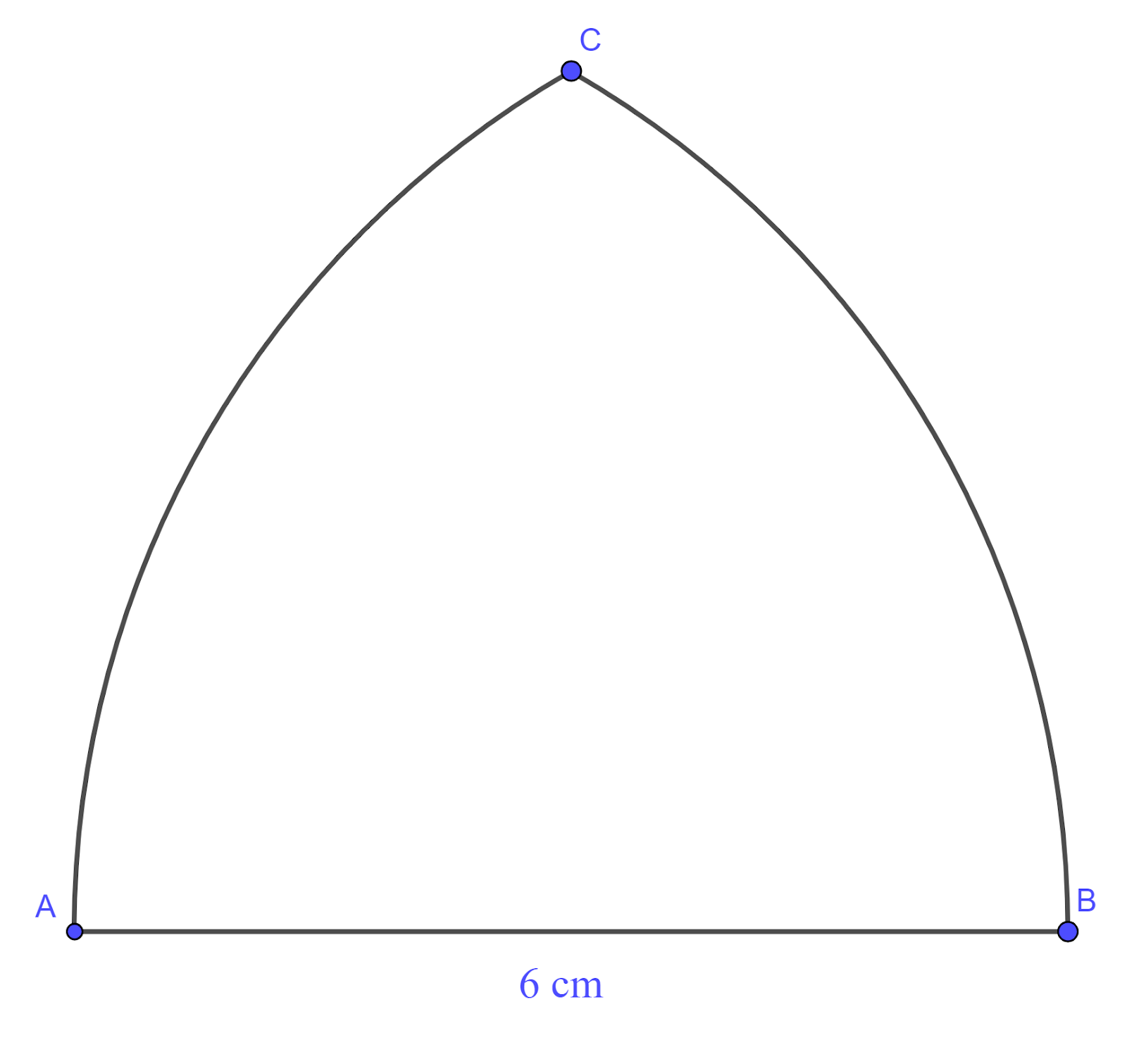
The diagram shows a metal plate ABC in which the sides are the straight line AB and the arcs AC and BC. The line AB has length `6` cm. The arc AC is part of a circle with centre B and radius `6` cm, and the arc BC is part of a circle with centre A and radius `6` cm.
a. Find the perimeter of the plate, giving your answer in terms of `pi`.
b. Find the area of the plate, giving your answer in terms of `pi` and `sqrt3`.
Hard
Mark as Complete
Mark Scheme
Question 17
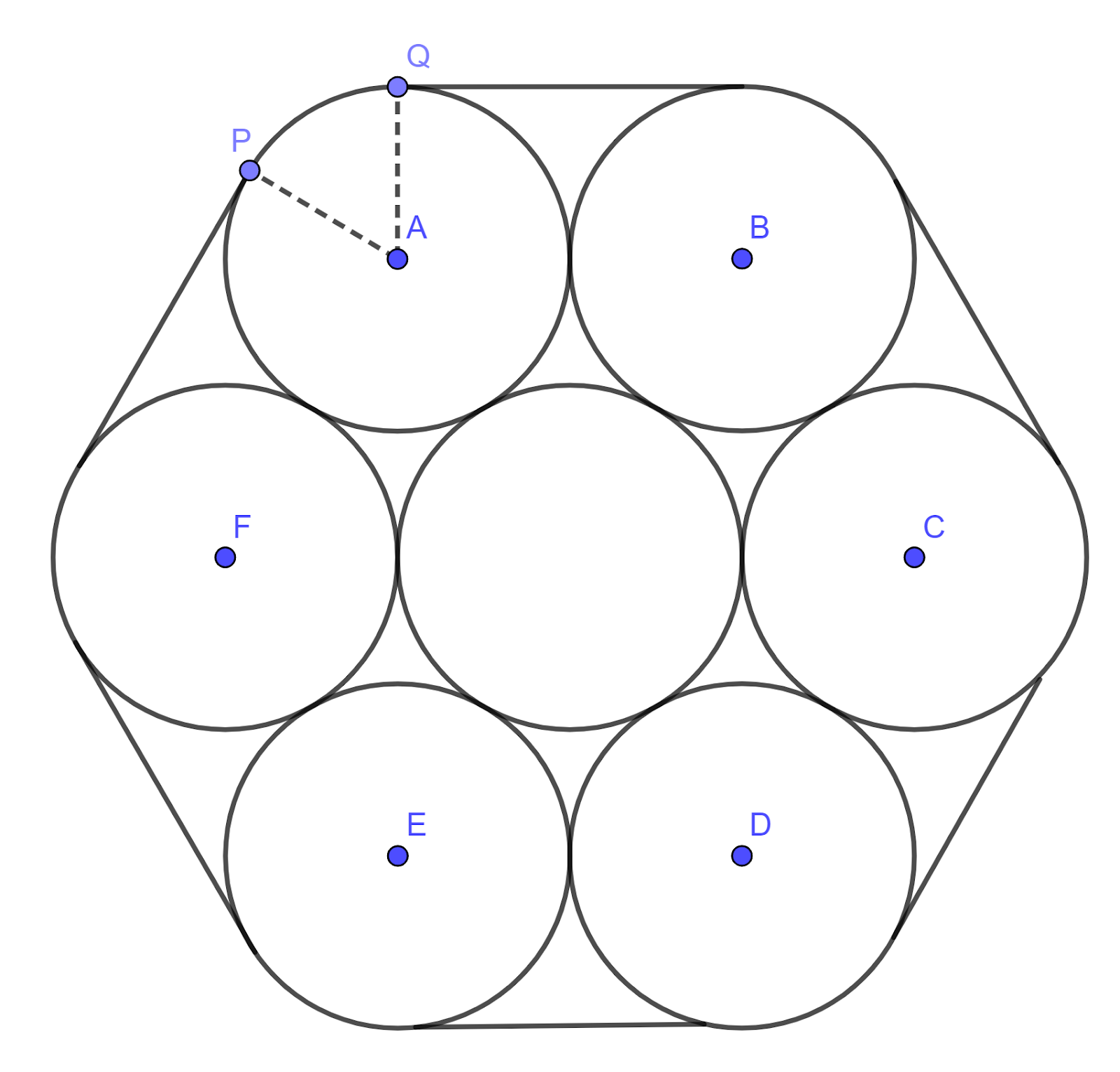
The diagram shows a cross-section of seven cylindrical pipes, each of radius `20` cm, held together by a thin rope which is wrapped tightly around the pipes. The centres of the six outer pipes are A, B, C, D, E and F. Points P and Q are situated where straight sections of the rope meet the pipe with centre A.
a. Show that angle PAQ `=1/3pi` radians.
b. Find the length of the rope.
c. Find the area of the hexagon ABCDEF, giving your answer in terms of `sqrt3`.
d. Find the area of the complete region enclosed by the rope.
Hard
Mark as Complete
Mark Scheme
Question 18
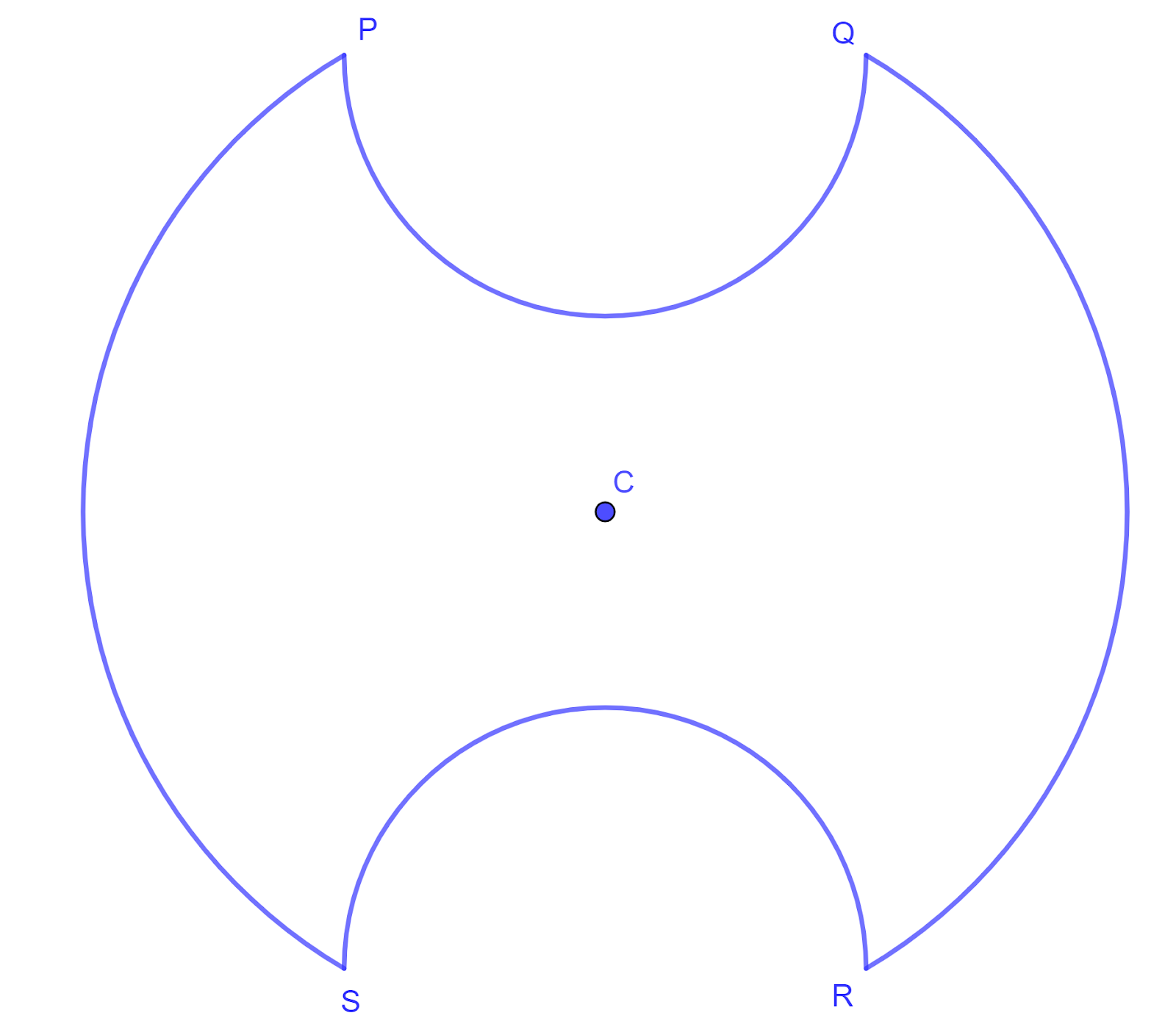
The diagram shows a symmetrical metal plate. The plate is made by removing two identical pieces from a circular disc with centre C. The boundary of the plate consists of two arcs PS and QR of the original circle and two semicircles with PQ and RS as diameters. The radius of the circle with centre C is `4` cm, and PQ = RS = `4` cm also.
a. Show that angle PCS `=2/3pi` radians
b. Find the exact perimeter of the plate
c. Show that the area of the plate is `(20/3pi+8sqrt3)` cm2
Hard
Mark as Complete
Mark Scheme
Question 19
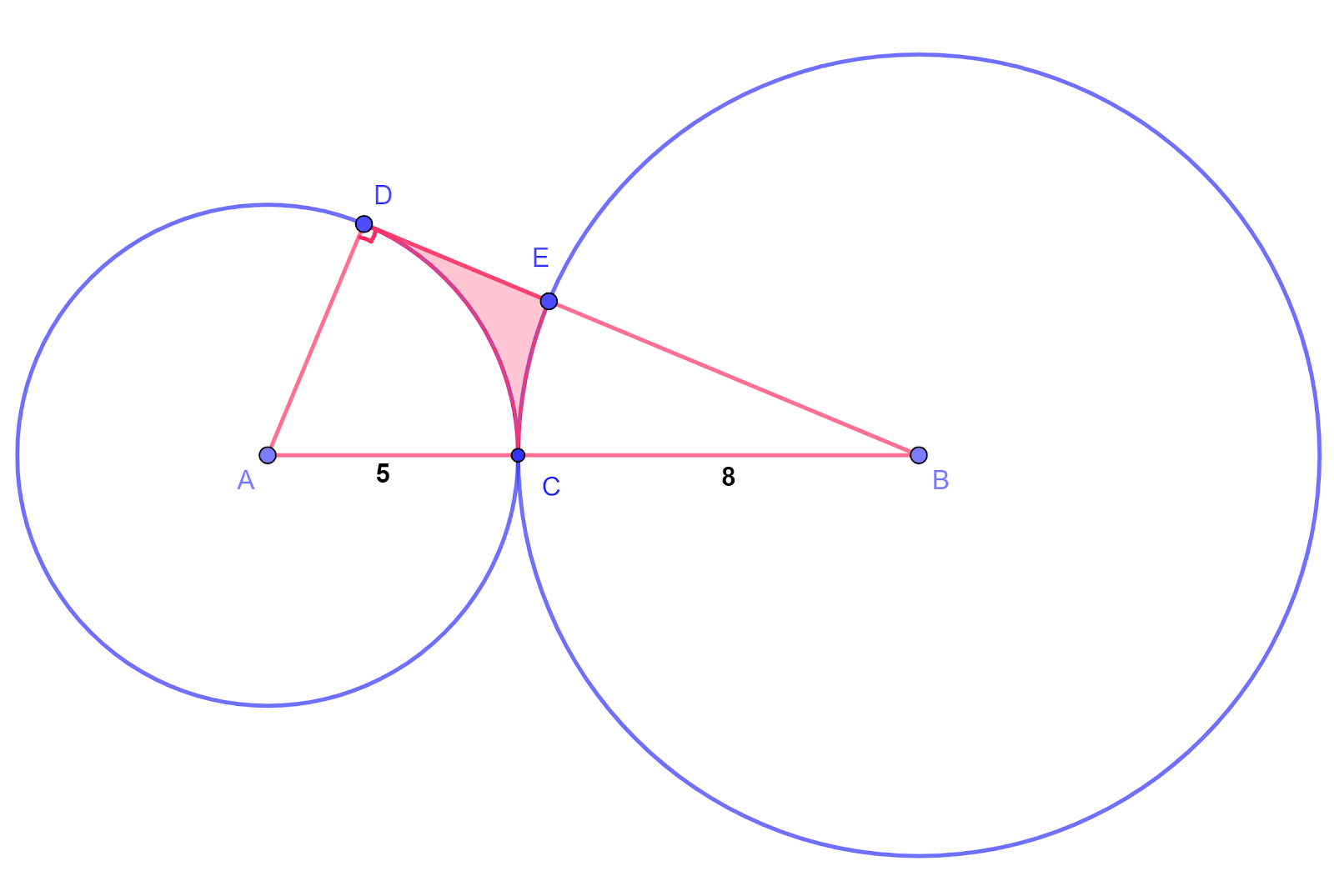
The diagram shows a circle with centre A of radius `5` cm and a circle with centre B of radius `8` cm. The circles touch at the point C so that ACB is a straight line. The tangent at the point D on the smaller circle intersects the larger circle at E and passes through B.
a. Find the perimeter of the shaded region.
b. Find the area of the shaded region.
Medium
Mark as Complete
Mark Scheme
Question 20
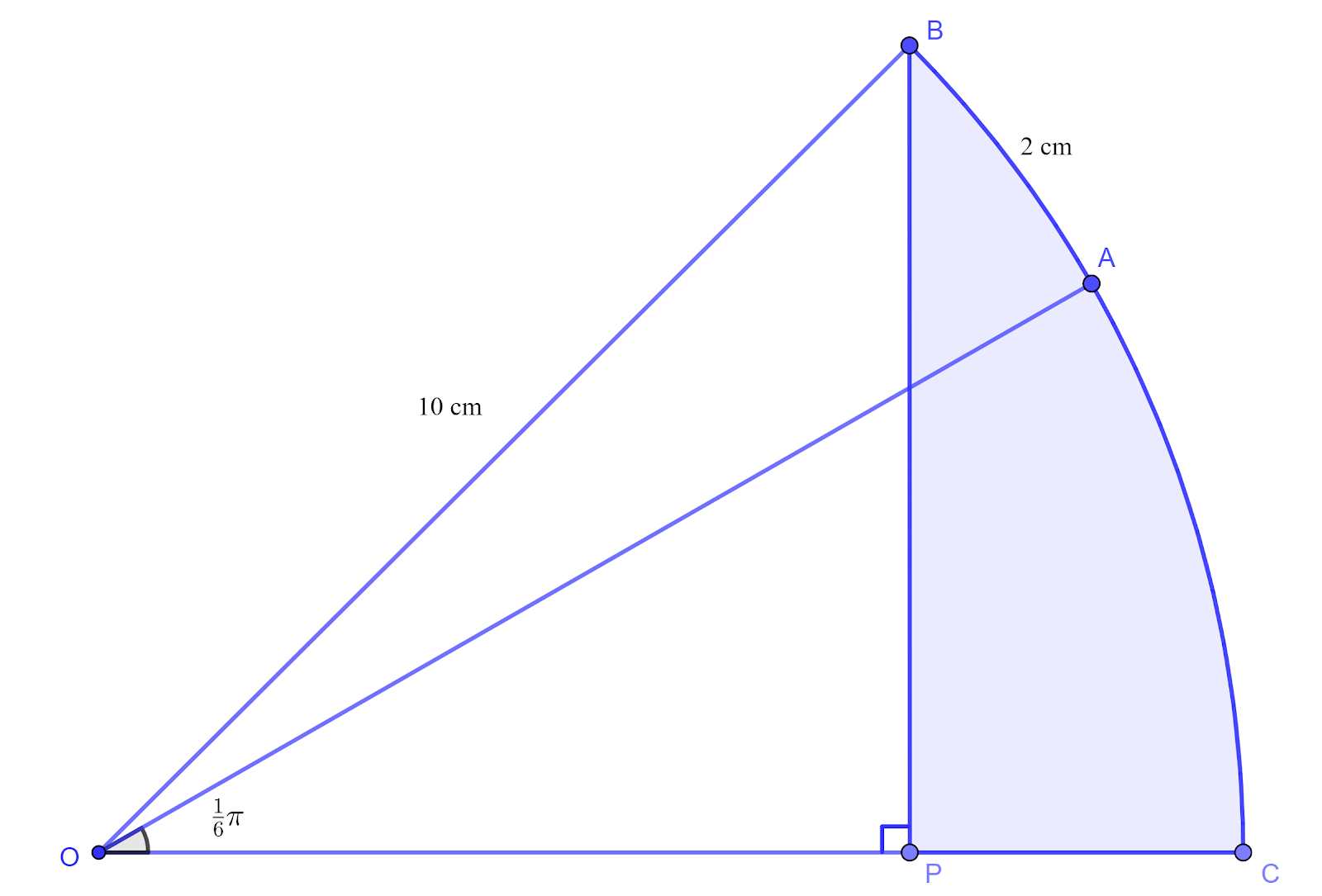
The diagram shows a sector OBAC of a circle with centre O and radius `10` cm. The point P lies on OC and BP is perpendicular to OC. Angle AOC `=1/6pi` and the length of the arc AB is `2` cm.
a. Find the angle BOC.
b. Hence find the area of the shaded region BPC giving your answer correct to 3 significant figures.
Medium
Mark as Complete
Mark Scheme
Question 1
Calculate the length of BC

ABC is a right-angled triangle
`tan 1` radian = `frac{BC}{5}`
`BC = 5 × tan 1`
`BC = 7.79` cm (to 3 significant figures)
Question 2
Find, in terms of `pi`, the arc length of a sector of:
a. radius `8` cm and angle `pi/4`
b. radius `7` cm and angle `frac{3pi}{7}`
a. Using arc length
`rtheta=8xxpi/4=2pi` cm
b. Using arc length
`rtheta=7xxfrac{3pi}{7}=3pi` cm
Question 3
Find the arc length of a sector of
a. radius `10` cm and angle `1.3` radians.
b. radius `3.5` cm and angle `0.65` radians.
a. Using arc length
`rθ = 10 × 1.3 = 13` cm
b. Using arc length
`rθ = 3.5 × 0.65 = 2.275` cm
Question 4
Find, in radians, the angle of a sector of:
a. radius `10` cm and arc length `5` cm
b. radius `12` cm and arc length `9.6` cm
a. Arc length `= rθ`
`5=10xxtheta`
`theta=5/10`
`theta=0.5` radians
a. Arc length `= rθ`
`9.6=12xxtheta`
`theta=9.6/12`
`theta=0.8` radians
Question 5
The High Roller Ferris wheel in the USA has a diameter of `158.5` metres. Calculate the distance travelled by a capsule as the wheel rotates through `pi/16` radians.
The radius of the Ferris wheel
`158.5/2=79.25` m
Using arc length to calculate the distance traveled
`79.25xxpi/16=15.6` m
Question 6
Find the perimeter of each of these sectors.
a.

b.

a. Perimeter of the sector
`rtheta+2r`
`=5xx2.1+2xx5`
`=20.5` cm
b. Perimeter of the sector
`rtheta+2r`
`=8xx4.3+2xx8`
`=50.4` cm
Question 7

The circle has radius 6 cm and centre O. PQ is a tangent to the circle at the point P. QRO is a straight line. Find:
a. angle POQ, in radians
b. the length of QR
c. the perimeter of the shaded area
a. Angle POQ
`tantheta=frac{PQ}{OP}`
`tantheta=8/6`
`theta=tan^-1(8/6)`
`theta=0.927` radians (to 3 significant figures)
b. The length of QO using Pythagoras
`QO^2=PQ^2+OP^2`
`QO=+-sqrt(PQ^2+OP^2)`
`QO=+-sqrt(8^2+6^2)`
`QO=10` cm (as QO is the length)
The length of QR
`QO-RO=10-6=4` cm
c. Perimeter of the shaded region
`arcPR+PQ+QR`
`=6xxtheta+8+4`
`=17.6` cm (to 3 significant figures)
Question 8

The circle has radius `7` cm and centre O. AB is a chord and angle AOB `=2` radians. Find:
a. the length of arc AB
b. the length of chord AB
c. the perimeter of the shaded segment
a. The length of arc AB
`rtheta=7xx2=14` cm
b. The length of chord AB using law of cosine
`AB=+-sqrt(BO^2+AO^2-2(BO)(AO)cosO`
`AB=+-sqrt(7^2+7^2-2(7)(7)cos2`
`AB=11.8` cm (to 3 significant figures, AB is the length)
c. The perimeter of the shaded segment
= arc AB + chord AB
`=14+11.8`
`=25.8` cm (to 3 significant figures)
Question 9

ABCD is a rectangle with AB `= 5` cm and BC `= 24` cm. O is the midpoint of BC. OAED is a sector of a circle, centre O. Find:
a. the length of AO
b. angle AOD, in radians
c. the perimeter of the shaded region
a. The length of AO using Pythagoras
`AO^2=AB^2+BO^2`
`AO=+-sqrt(AB^2+BO^2`
`AO=+-sqrt(5^2+12^2`
`AO=13` cm (as AO is the length)
b.
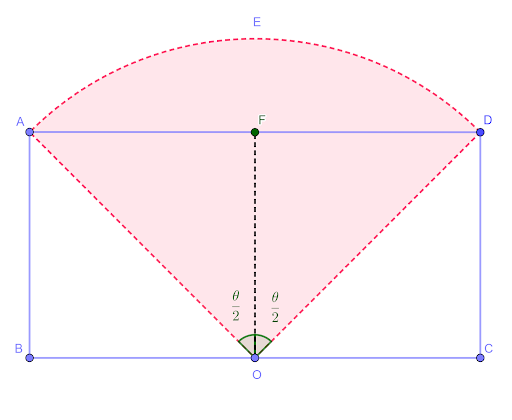
Angle AOD
`tanfrac{theta}{2}=frac{AF}{OF}`
`tanfrac{theta}{2}=frac{24}{2xx5}`
`theta/2=tan^-1(24/10)`
`theta=2tan^-1(24/10)`
`theta=2.35` radians (to 3 significant figures)
c. Perimeter of the shaded region
arc AED + AO +OD
`=13xxtheta+13+13`
`=56.6` cm (to 3 significant figures)
Question 10
Find, in terms of `pi`, the area of a sector of:
a. radius `10` cm and angle `frac{2pi}{5}` radians
b. radius `4.5` cm and angle `frac{2pi}{9}` radians
a. Area of sector
`1/2r^2theta=1/2xx10^2xxfrac{2pi}{5}=20pi` cm2
b. Area of sector
`1/2r^2theta=1/2xx4.5^2xxfrac{2pi}{9}=2.25pi` cm2
Question 11
AOB is a sector of a circle, centre O, with radius `8` cm. The length of arc AB is `10` cm. Find:
a. angle AOB, in radians
b. the area of the sector AOB
a. Angle AOB
`theta=frac{"arc length"}{r}`
`theta=10/8`
`theta=1.25` radians
b. Area of sector AOB
`1/2r^2theta=1/2xx8^2xx1.25=40` cm2
Question 12

The diagram shows a sector, POQ, of a circle, centre O, with radius `4` cm. The length of arc PQ is `7` cm. The lines PX and QX are tangents to the circle at P and Q, respectively.
a. Find angle POQ, in radians
b. Find the length of PX
c. Find the area of the shaded region.
a. Angle POQ
Arc length = rθ
`7=4theta`
`theta=1.75` radians
b.
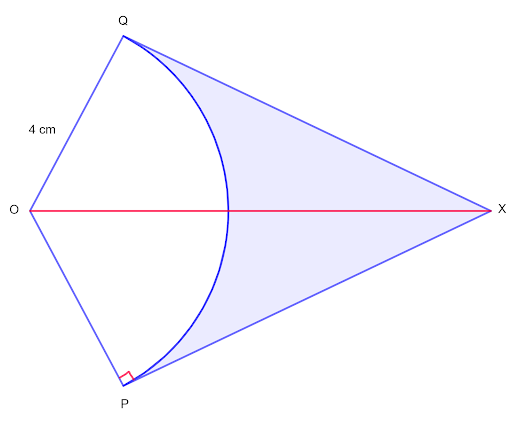
Angle POX
`theta/2=1.75/2=0.875` radians
POX is a right-angled triangle (PX is a tangent)
`tanfrac{theta}{2}=frac{PX}{OP}`
`tan0.875=frac{PX}{4}`
`PX=4.79` cm (to 3 significant figures)
c. The area of the shaded region
2 × area △POX – area of sector OPQ
`=2xx1/2xxOPxxPX-1/2xxr^2xxtheta`
`=4xx4.79-1/2xx4^2xx1.75`
`=5.16` cm2
Question 13

The diagram shows a sector, POR, of a circle, centre O, with radius `8` cm and sector angle `pi/3` radians. The lines OR and QR are perpendicular and OPQ is a straight line.
Find the exact area of the shaded region.
The length of RQ
`tanROQ=frac{RQ}{OR}`
`tanfrac{pi}{3}=frac{RQ}{8}`
`RQ=8sqrt3` cm
The area of the shaded region
Area △OQR – area of sector OPR
`=1/2xx"base"xx"perpendicular height"-1/2xxr^2xxtheta`
`=1/2xx8xx8sqrt3-1/2xx8^2xxpi/3`
`32sqrt3-frac{32pi}{3}` cm2
Question 14

The diagram shows a sector, EOG, of a circle, centre O, with radius `r` cm. The line GF is a tangent to the circle at G, and E is the midpoint of OF.
a. The perimeter of the shaded region is `P` cm. Show that `P=r/3(3+3sqrt3+pi)`
b. The area of the shaded region is `A` cm2. Show that `A=r^2/6(3sqrt3-pi)`
a. The length of GF using Pythagoras
`GF=sqrt(OF^2-OG^2)`
`GF=sqrt((2r)^2-r^2`
`GF=sqrt3r` (as GF is the length)
Angle GOF
`costheta=frac{OG}{OF}=frac{r}{2r}`
`theta=cos^-1(1/2)=pi/3`
The perimeter of the shaded region
P = arc EG + EF + GF
P = rθ + EF + GF
`P=rxxpi/3+r+sqrt3r`
`P=r/3(3+3sqrt3+pi)`
b. The area of the shaded region
Area △OGF – area of sector OGE
`=1/2xx"base"xx"perpendicular height"-1/2xxr^2xxtheta`
`=12xxsqrt3rxxr-1/2xxr^2xxpi/3`
`=frac{sqrt3r^2}{2}-frac{pir^2}{6}`
`=r^2/6(3sqrt3-pi)` cm2
Question 15

The diagram shows a sector AOB which is part of a circle with centre O and radius `6` cm and with angle AOB `=0.8` radians. The point C on OB is such that AC is perpendicular to OB. The arc CD is part of a circle with centre O, where D lies on OA.
Find the area of the shaded region.
a. The length of OC in ΔOAC
`costheta=frac{OC}{OA}`
`cos0.8=frac{OC}{6}`
`OC=6xxcos0.8=4.18` cm
The area of the shaded region
Area of ΔOAC – area of sector OCD
`=1/2xxOCxxACxxsintheta-1/2xxOC^2xxtheta`
`=1/2xx4.18xx6xxsin0.8-1/2xx(4.18)^2xx0.8`
`=2.01` cm2
Question 16

The diagram shows a metal plate ABC in which the sides are the straight line AB and the arcs AC and BC. The line AB has length `6` cm. The arc AC is part of a circle with centre B and radius `6` cm, and the arc BC is part of a circle with centre A and radius `6` cm.
a. Find the perimeter of the plate, giving your answer in terms of `pi`.
b. Find the area of the plate, giving your answer in terms of `pi` and `sqrt3`.
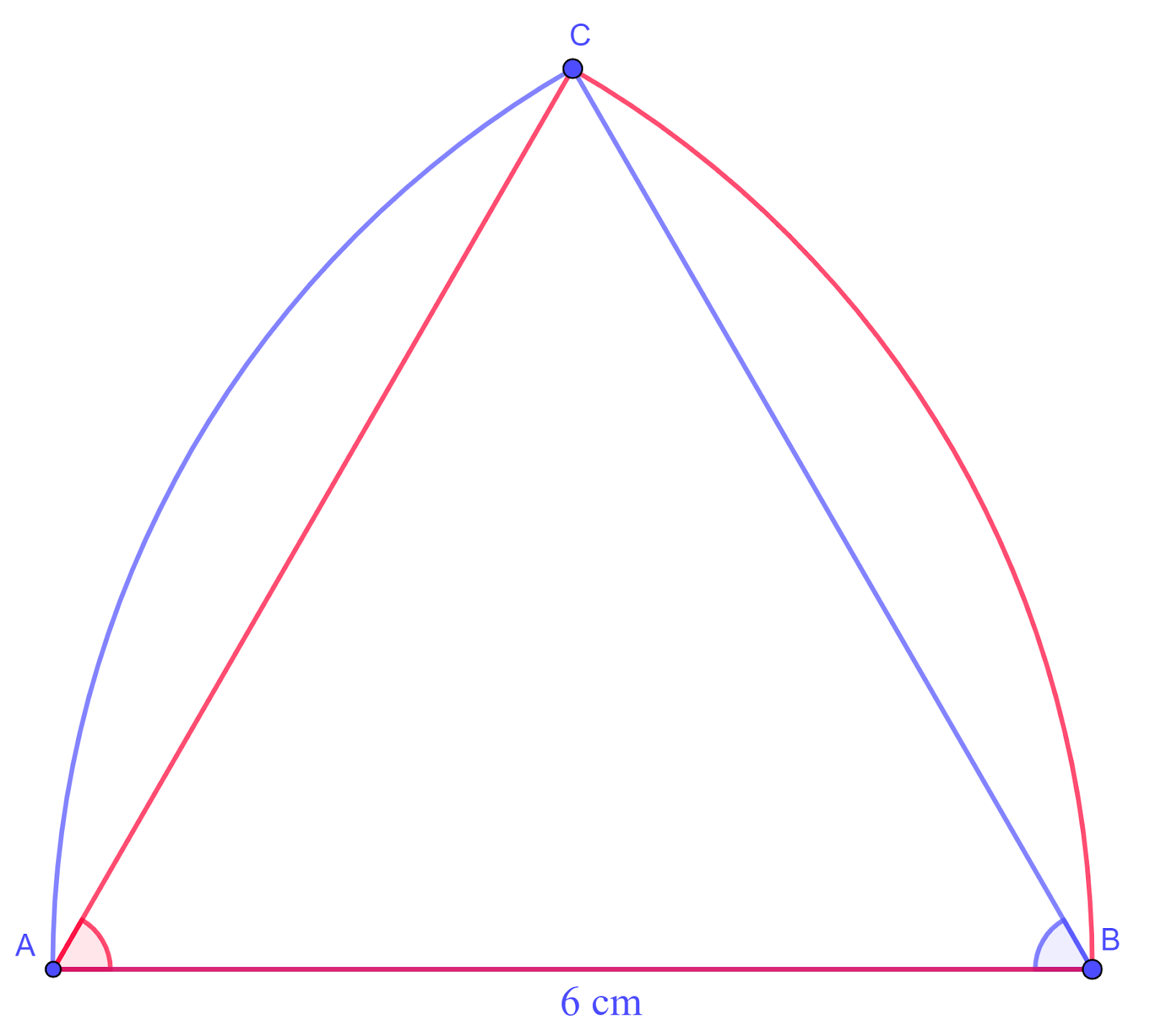
Each internal angle of ΔABC `=pi/3` (ABC is an equilateral triangle)
Perimeter of the plate
Length of AB + arc length of AC + arc length of CB
`=6+6xxpi/3+6xxpi/3=6+4pi` cm
b. Area of the plate
2 × area of sector ABC – area of ΔABC
`=2xx(1/2xx6^2xxpi/3)-1/2xx6xx6xxsinfracpi3`
`=12pi-9sqrt3` cm2
Question 17

The diagram shows a cross-section of seven cylindrical pipes, each of radius `20` cm, held together by a thin rope which is wrapped tightly around the pipes. The centres of the six outer pipes are A, B, C, D, E and F. Points P and Q are situated where straight sections of the rope meet the pipe with centre A.
a. Show that angle PAQ `=1/3pi` radians.
b. Find the length of the rope.
c. Find the area of the hexagon ABCDEF, giving your answer in terms of `sqrt3`.
d. Find the area of the complete region enclosed by the rope.
a. Angle of a full circle centre A is `2pi`
There are 6 sectors that make up a full circle
`6xx/_PAQ=2pi`
Angle PAQ
`frac{2pi}{6}=1/3pi`
b. The length of each straight section of the rope
`2xx20=40` cm
The arc length of each curved section round each pipe
`rtheta=20xxpi/3=20/3pi`
The total length of the rope
`6xx40+6xx20/3pi`
`=240+40pi`
`366` cm
c.
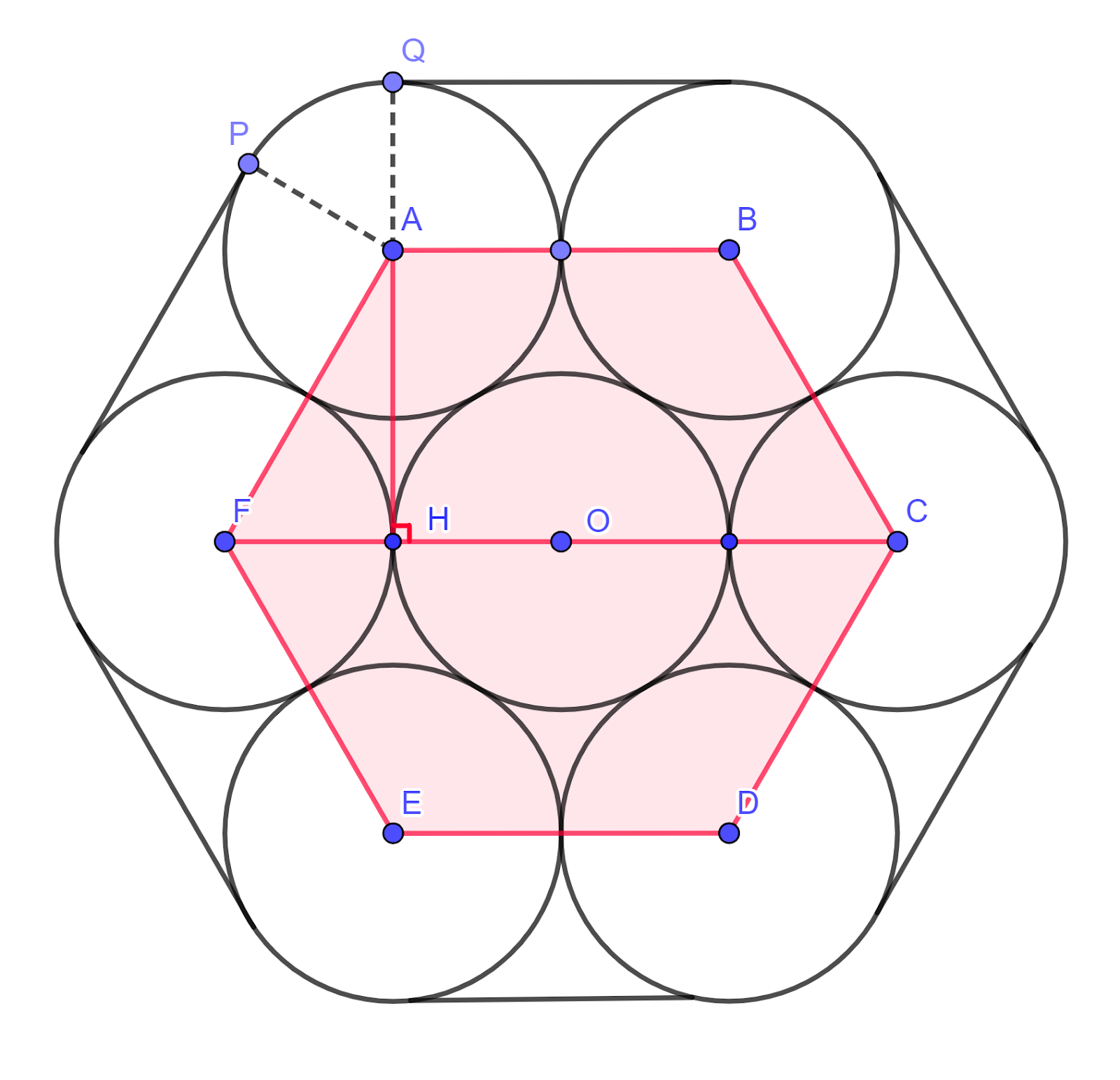
The length of AH
`sqrt(AF^2-FH^2)=sqrt(40^2-20^2)=20sqrt3` cm
The area of the hexagon ABCDEF
2 × area of trapezium ABCF
`=2xx1/2(AB+FC)xxAH`
`=2xx1/2(40+80)xx20sqrt3`
`=2400sqrt3` cm2
d.
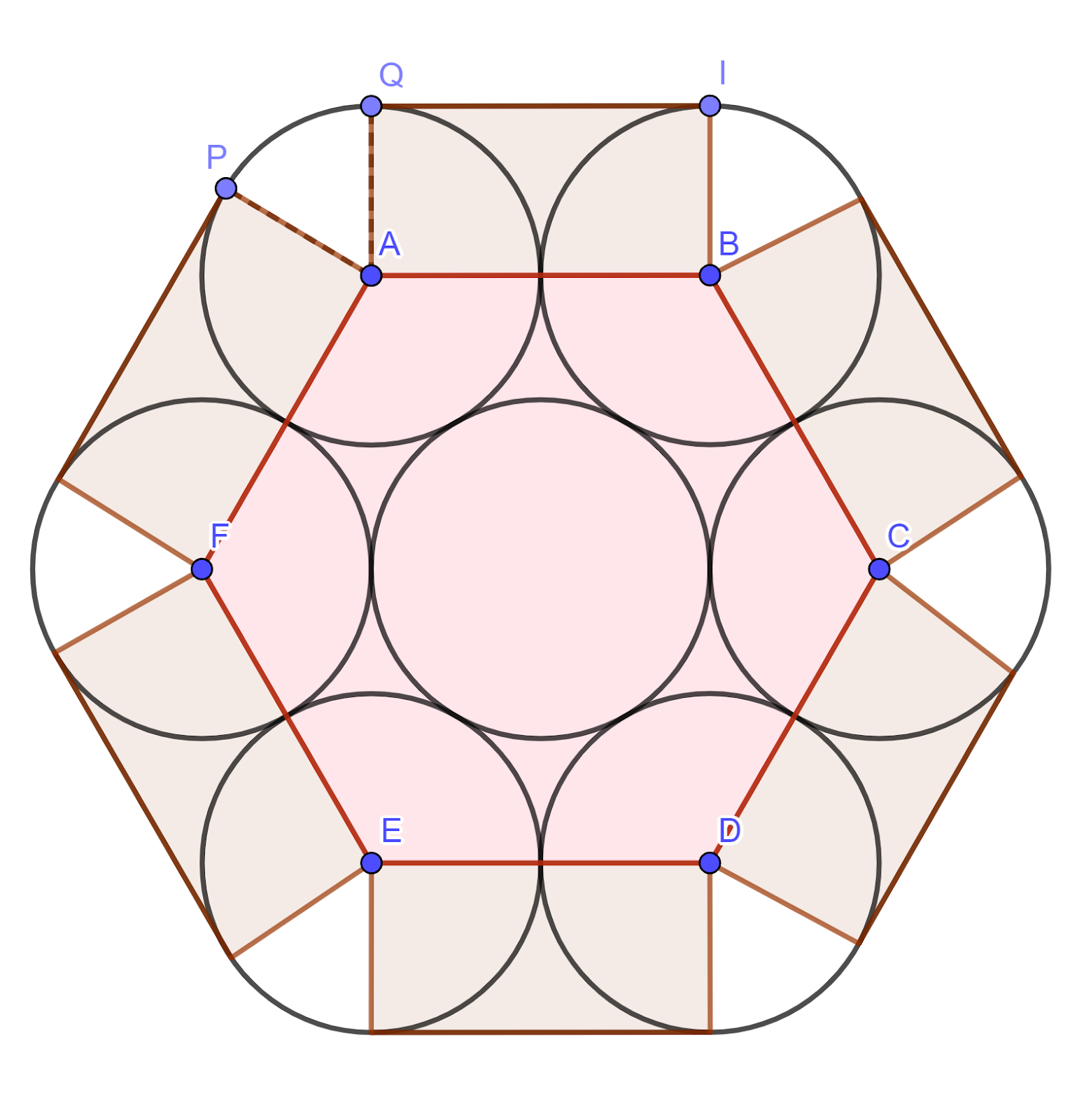
The area of sector PAQ
`1/2r^2theta=1/2xx20^2xx1/3pi=200/3pi` cm2
The area of AQIB
`20xx40=800` cm2
The area of the complete region enclosed by the rope
Area of ABCDEF + 6 × area of PAQ + 6 × area of AQIB
`=2400sqrt3+6xx200/3pi+6xx800=10214` cm2
Question 18

The diagram shows a symmetrical metal plate. The plate is made by removing two identical pieces from a circular disc with centre C. The boundary of the plate consists of two arcs PS and QR of the original circle and two semicircles with PQ and RS as diameters. The radius of the circle with centre C is `4` cm, and PQ = RS = `4` cm also.
a. Show that angle PCS `=2/3pi` radians
b. Find the exact perimeter of the plate
c. Show that the area of the plate is `(20/3pi+8sqrt3)` cm2
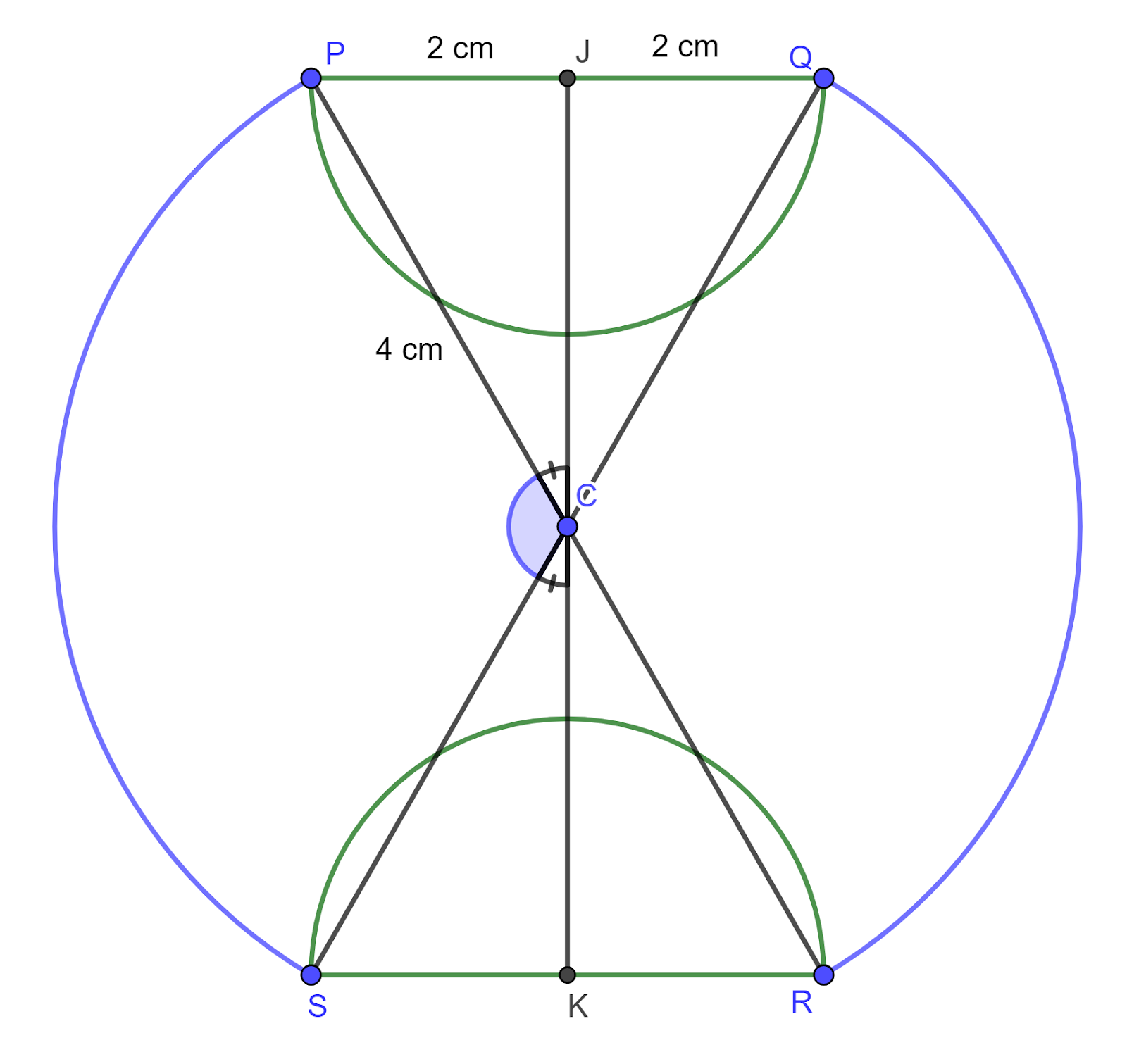
a. Angle JCP
`sinJCP=frac{PJ}{PC}`
`sinJCP=2/4`
`/_JCP=sin^-1(2/4)`
`/_JCP=1/6pi`
Similarly, angle KCS `=1/6pi`
Angle PCS
`pi-/_JCP-/_KCS`
`=pi-1/6pi-1/6pi=2/3pi`
b. The perimeter of the plate
Arc PS + arc QR + arc PQ + arc SR
`=2xxrxx/_PCS+2xxfrac{PQ}{2}xxpi`
`=2xx4xx2/3pi+2xx4/2xxpi`
`=28/3pi` cm
c. The area of large sector PCS
`1/2xxPC^2xx/_PCS`
`=1/2xx4^2xx2/3pi`
`=16/3pi` cm2
The area of small semicircle
`1/2xxPQ^2xxpi`
`=1/2xx2^2xxpi`
`=2pi` cm2
The angle of PCQ
`2xx1/6pi=1/3pi`
The area of ΔCPQ
`1/2xxPCxxQCxxsin/_PCQ`
`=1/2xx4xx4xxsin(1/3pi)`
`=4sqrt3` cm2
The area of the plate
2 × large sector PCS + 2 × ΔCPQ − 2 × small semicircle
`=2xx16/3pi+2xx4sqrt3-2xx2pi`
`=20/3pi+8sqrt3` cm2
Question 19

The diagram shows a circle with centre A of radius `5` cm and a circle with centre B of radius `8` cm. The circles touch at the point C so that ACB is a straight line. The tangent at the point D on the smaller circle intersects the larger circle at E and passes through B.
a. Find the perimeter of the shaded region.
b. Find the area of the shaded region.
a. The length of DB
`DB=sqrt(AB^2-AD^2)`
`DB=sqrt((5+8)^2-5^2`
`DB=12` cm
Angle DAB
`tanA=frac{DB}{DA}`
`tanA=12/5`
`A=tan^-1(12/5)`
`A=1.18` (to 3 significant figures)
Angle DBA
`tanB=frac{DA}{DB}`
`tanB=5/12`
`B=tan^-1(5/12)`
`B=0.395` (to 3 significant figures)
The perimeter of the shaded region
DE + arc EC + arc CD
`=DB-BE+ACxx/_A+BCxx/_B`
`=12-8+5xx/_A+8xx/_B`
`=13.0` cm
b. The area of the shaded region
Area △DAB – area sector DAC – area sector DBA
`=1/2xxDAxxDB-1/2xxAC^2xx/_A-1/2xxBC^2xx/_B`
`=1/2xx5xx12-1/2xx5^2xx/_A-1/2xx8^2xx/_B`
`=2.67` cm2
Question 20

The diagram shows a sector OBAC of a circle with centre O and radius `10` cm. The point P lies on OC and BP is perpendicular to OC. Angle AOC `=1/6pi` and the length of the arc AB is `2` cm.
a. Find the angle BOC.
b. Hence find the area of the shaded region BPC giving your answer correct to 3 significant figures.
a. Angle AOB using arc length
`frac{AB}{OB}=2/10=1/5`
Angle BOC
`1/5+1/6pi=frac{5pi+6}{30}`
b. The length of BP
`sinBOC=frac{BP}{OB}`
`sinfrac{5pi+6}{30}=frac{BP}{10}`
`BP=10sinfrac{5pi+6}{30}` cm
The length of OP
`cosBOC=frac{OP}{OB}`
`cosfrac{5pi+6}{30}=frac{OP}{10}`
`OP=10cosfrac{5pi+6}{30}` cm
The area of the shaded region BPC
Area of sector BOC – area △OBP
`=1/2xxOB^2xx/_BOC-1/2xxOPxxBP`
`=1/2xx10^2xxfrac{5pi+6}{30}-1/2xx10cosfrac{5pi+6}{30}xx10sinfrac{5pi+6}{30}`
`=11.4` cm2
Question 1
Calculate the length of BC

Question 2
Find, in terms of `pi`, the arc length of a sector of:
a. radius `8` cm and angle `pi/4`
b. radius `7` cm and angle `frac{3pi}{7}`
Question 3
Find the arc length of a sector of
a. radius `10` cm and angle `1.3` radians.
b. radius `3.5` cm and angle `0.65` radians.
Question 4
Find, in radians, the angle of a sector of:
a. radius `10` cm and arc length `5` cm
b. radius `12` cm and arc length `9.6` cm
Question 5
The High Roller Ferris wheel in the USA has a diameter of `158.5` metres. Calculate the distance travelled by a capsule as the wheel rotates through `pi/16` radians.
Question 6
Find the perimeter of each of these sectors.
a.

b.

Question 7

The circle has radius 6 cm and centre O. PQ is a tangent to the circle at the point P. QRO is a straight line. Find:
a. angle POQ, in radians
b. the length of QR
c. the perimeter of the shaded area
Question 8

The circle has radius `7` cm and centre O. AB is a chord and angle AOB `=2` radians. Find:
a. the length of arc AB
b. the length of chord AB
c. the perimeter of the shaded segment
Question 9

ABCD is a rectangle with AB `= 5` cm and BC `= 24` cm. O is the midpoint of BC. OAED is a sector of a circle, centre O. Find:
a. the length of AO
b. angle AOD, in radians
c. the perimeter of the shaded region
Question 10
Find, in terms of `pi`, the area of a sector of:
a. radius `10` cm and angle `frac{2pi}{5}` radians
b. radius `4.5` cm and angle `frac{2pi}{9}` radians
Question 11
AOB is a sector of a circle, centre O, with radius `8` cm. The length of arc AB is `10` cm. Find:
a. angle AOB, in radians
b. the area of the sector AOB
Question 12

The diagram shows a sector, POQ, of a circle, centre O, with radius `4` cm. The length of arc PQ is `7` cm. The lines PX and QX are tangents to the circle at P and Q, respectively.
a. Find angle POQ, in radians
b. Find the length of PX
c. Find the area of the shaded region.
Question 13

The diagram shows a sector, POR, of a circle, centre O, with radius `8` cm and sector angle `pi/3` radians. The lines OR and QR are perpendicular and OPQ is a straight line.
Find the exact area of the shaded region.
Question 14

The diagram shows a sector, EOG, of a circle, centre O, with radius `r` cm. The line GF is a tangent to the circle at G, and E is the midpoint of OF.
a. The perimeter of the shaded region is `P` cm. Show that `P=r/3(3+3sqrt3+pi)`
b. The area of the shaded region is `A` cm2. Show that `A=r^2/6(3sqrt3-pi)`
Question 15

The diagram shows a sector AOB which is part of a circle with centre O and radius `6` cm and with angle AOB `=0.8` radians. The point C on OB is such that AC is perpendicular to OB. The arc CD is part of a circle with centre O, where D lies on OA.
Find the area of the shaded region.
Question 16

The diagram shows a metal plate ABC in which the sides are the straight line AB and the arcs AC and BC. The line AB has length `6` cm. The arc AC is part of a circle with centre B and radius `6` cm, and the arc BC is part of a circle with centre A and radius `6` cm.
a. Find the perimeter of the plate, giving your answer in terms of `pi`.
b. Find the area of the plate, giving your answer in terms of `pi` and `sqrt3`.
Question 17

The diagram shows a cross-section of seven cylindrical pipes, each of radius `20` cm, held together by a thin rope which is wrapped tightly around the pipes. The centres of the six outer pipes are A, B, C, D, E and F. Points P and Q are situated where straight sections of the rope meet the pipe with centre A.
a. Show that angle PAQ `=1/3pi` radians.
b. Find the length of the rope.
c. Find the area of the hexagon ABCDEF, giving your answer in terms of `sqrt3`.
d. Find the area of the complete region enclosed by the rope.
Question 18

The diagram shows a symmetrical metal plate. The plate is made by removing two identical pieces from a circular disc with centre C. The boundary of the plate consists of two arcs PS and QR of the original circle and two semicircles with PQ and RS as diameters. The radius of the circle with centre C is `4` cm, and PQ = RS = `4` cm also.
a. Show that angle PCS `=2/3pi` radians
b. Find the exact perimeter of the plate
c. Show that the area of the plate is `(20/3pi+8sqrt3)` cm2
Question 19

The diagram shows a circle with centre A of radius `5` cm and a circle with centre B of radius `8` cm. The circles touch at the point C so that ACB is a straight line. The tangent at the point D on the smaller circle intersects the larger circle at E and passes through B.
a. Find the perimeter of the shaded region.
b. Find the area of the shaded region.
Question 20

The diagram shows a sector OBAC of a circle with centre O and radius `10` cm. The point P lies on OC and BP is perpendicular to OC. Angle AOC `=1/6pi` and the length of the arc AB is `2` cm.
a. Find the angle BOC.
b. Hence find the area of the shaded region BPC giving your answer correct to 3 significant figures.