Trigonometry

a. Given that `costheta=4/5` and that `θ` is acute, find the exact value of:

`frac{1-sin^2theta}{costheta}`

`frac{3-sintheta}{3+costheta}`

b. Given that `sintheta=1/4` and that `θ` is acute, find the exact value of:

`frac{sinthetacostheta}{tantheta}`

`1/tantheta+1/sintheta`

a.

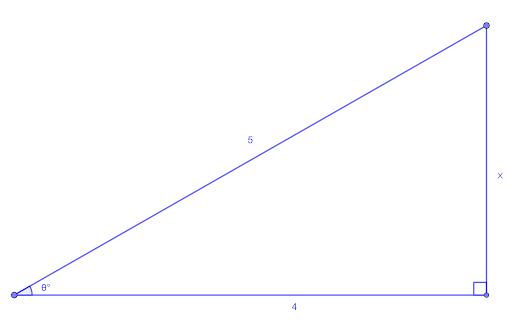
Use the triangle shown and Pythagoras’ theorem

`x=sqrt(5^2-4^2)=3`

`costheta=4/5`

`sintheta=3/5` 

`frac{1-sin^2theta}{costheta}=frac{cos^2theta}{costheta}=costheta=4/5` (as `sin^2x+cos^2x=1`)

`frac{3-sintheta}{3+costheta}=frac{15/5-3/5}{15/5+4/5}=frac{12/5}{19/5}=12/19`

b.

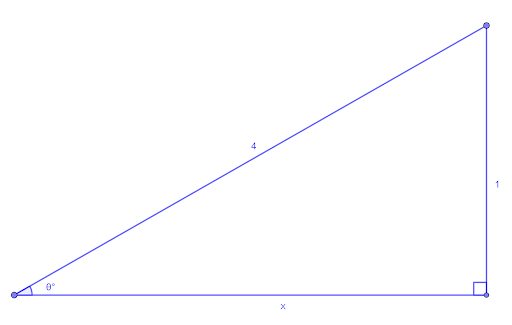
Use the triangle shown and Pythagoras’ theorem

`x=sqrt(4^2-1^2)=sqrt15`

`costheta=sqrt15/4`

`sintheta=1/4`

`tantheta=sintheta/costheta`

`frac{sinthetacostheta}{tantheta}=frac{sinthetacostheta}{sintheta/costheta}=cos^2theta=(costheta)^2=(sqrt15/4)^2=15/16`

`1/tantheta+1/sintheta=1/frac{sintheta}{costheta}+1/sintheta=frac{costheta+1}{sintheta}`

`=frac{sqrt15/4+1}{1/4}=frac{frac{sqrt15+4}{4}}{1/4}`

`=sqrt15+4`

Find the exact value of each of the following:

a. `frac{sin^2 45°}{2+tan60°}`

b. `frac{sin^2 30°+cos^2 30°}{2sin 45°cos 45°}`

c. `1/tan frac{pi}{4}-1/cos frac{pi}{3}`

d. `frac{cos frac{pi}{3}+ tan frac{pi}{6}}{sin frac{pi}{3}}`

a.

`frac{sin^2 45°}{2+tan 60°}`

`=frac{(1/sqrt2)^2}{2+sqrt3}=frac{1/2}{frac{2+sqrt3}{1}}=frac{1}{4+2sqrt3}`

`=frac{1}{4+2sqrt3}xxfrac{4-2sqrt3}{4-2sqrt3}=frac{4-2sqrt3}{4^2-(2sqrt3)^2` (as `(a+b)(a-b)=a^2-b^2`)

`=frac{4-2sqrt3}{16-12}=frac{4-2sqrt3}{4}=frac{2-sqrt3}{2}`

b. `frac{sin^2 30°+cos^2 30°}{2sin 45°cos 45°}`

`=frac{1}{2xx1/sqrt2xx1/sqrt2}=1` (as `sin^2x+cos^2x=1`)

c. `1/tan frac{pi}{4}-1/cos frac{pi}{3}`

`=1/1-frac{1}{1/2}=1-2=-1`

d. `frac{cos frac{pi}{3}+ tan frac{pi}{6}}{sin frac{pi}{3}}`

`frac{1/2+1/sqrt3}{sqrt3/2}=frac{frac{sqrt3+2}{2sqrt3}}{sqrt3/2}`

`=frac{2sqrt3+4}{6}=frac{sqrt3+2}{3}`

Draw a diagram showing the quadrant in which the rotating line OP lies for each of the following angles. On each diagram, indicate clearly the direction of rotation and state the acute angle that the line OP makes with the x-axis.

a. `-150°`

b. `frac{13pi}{9}`

a. `-150°` is a clockwise rotation

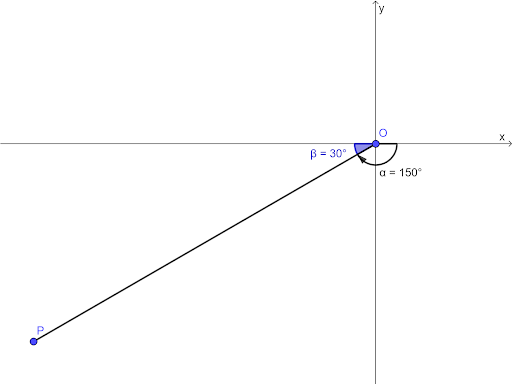
Acute angle made with x-axis `=30°`

b. `frac{13pi}{9}` is an anticlockwise rotation

`frac{13xx180°}{9}=13xx20°=260°`

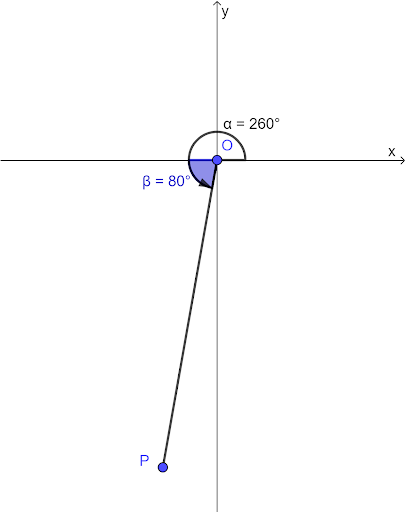
`frac{80°xxpi}{180°}=frac{4pi}{9}`

Acute angle made with x-axis `=frac{4pi}{9}`

Given that `sintheta=2/5` and that `θ` is obtuse, find the value of:

a. `costheta`

b. `tantheta`

The second quadrant `90° (`θ` is obtuse)

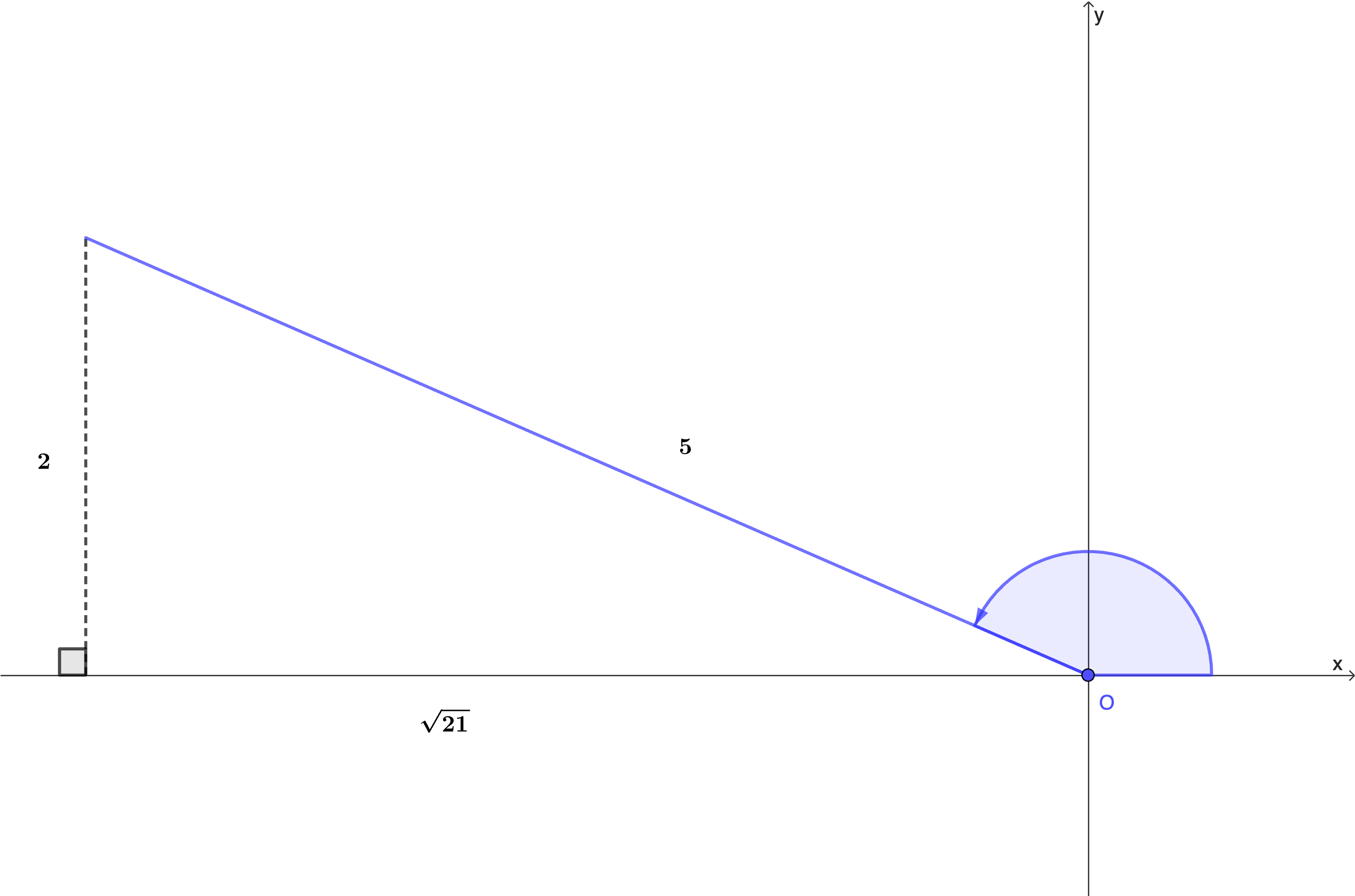
Using Pythagoras

`x=sqrt(5^2-2^2)=+-sqrt21`

`x=-sqrt21` (as `x<0`)

a. `costheta=frac{-sqrt21}{5}`

b. `tantheta=2/-sqrt21=-frac{2sqrt21}{21}`

Given that `tantheta=-5/12` and that `180°<=theta<=360°`, find the value of:

a. `sintheta`

b. `costheta`

`180°<=theta<=360°` are the quadrants III and IV 

tan is positive in the quadrant III, so `tantheta=-5/12` belongs to the quadrant IV

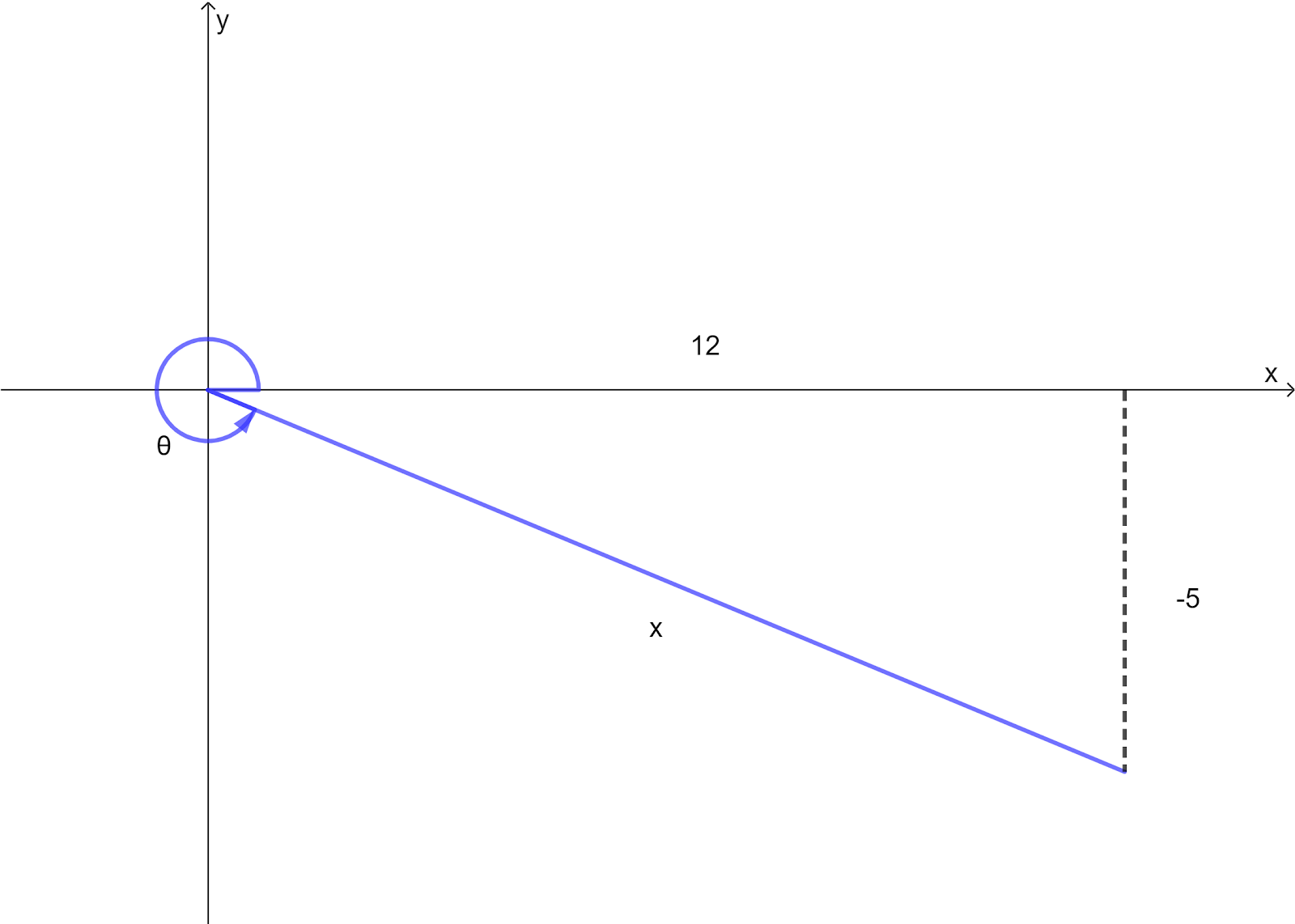
`x^2=12^2+(-5)^2`

`x=+-sqrt169`

`x=13` (`x>0` by definition)

a. `sintheta=-frac{5}{13}`

b. `costheta=12/13`

a. Sketch the graph of `y=2sinx` for `-pi<=x<=pi`. The straight line `y=kx` intersects this curve at the maximum point. 

b. Find the value of `k`. Give your answer in terms of `pi`. 

c. State the coordinates of the other points where the line intersects the curve.

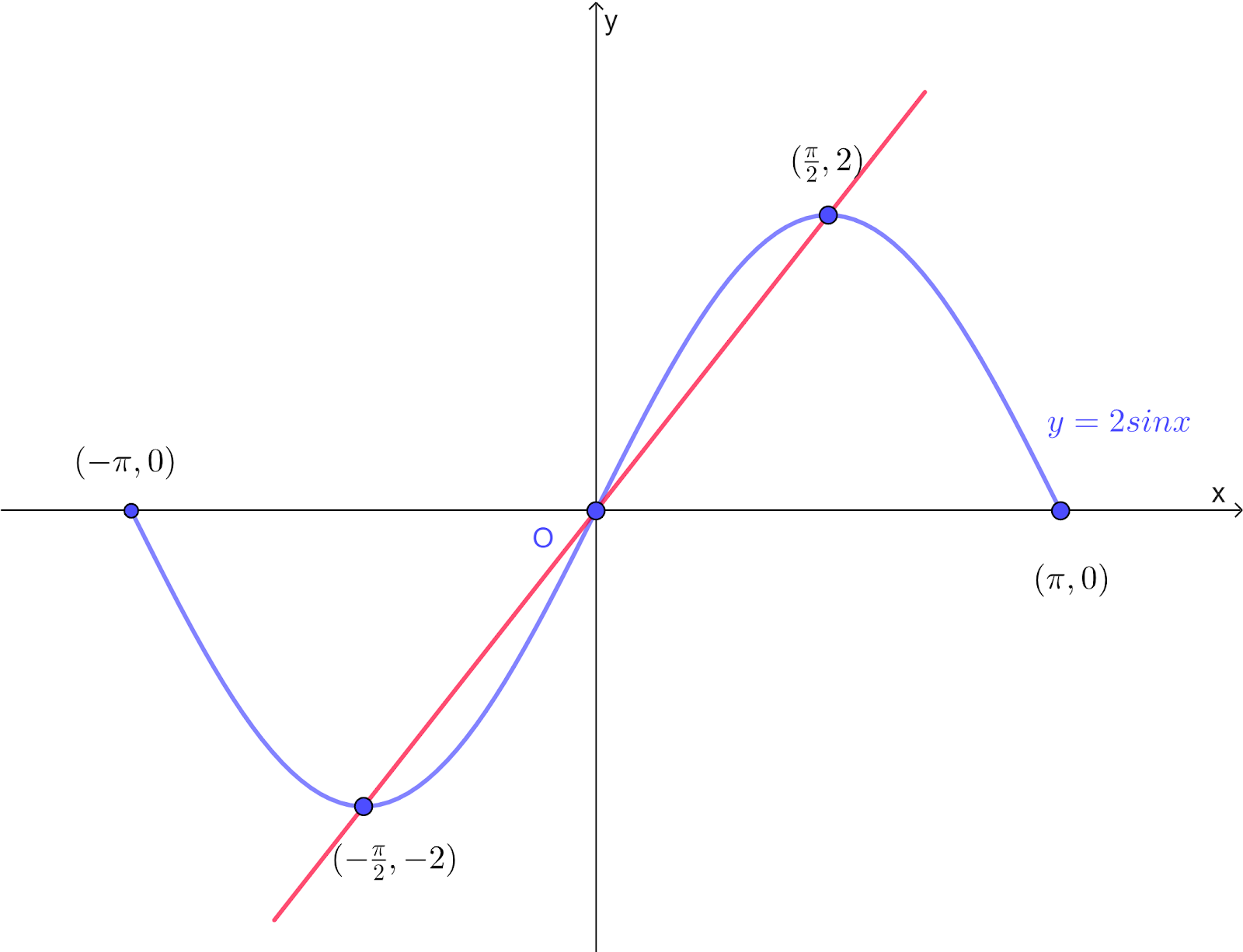
a. The graph of `y=sinx` (amplitude `=1`, period `= 2 π`) is transformed to the graph of `y=2sinx` by stretch factor `2`, parallel to the y-axis

All y-coordinates of the original graph are multiplied by `2`

The maximum turning point on `y=sinx` for `-pi<=x<=pi` is at `(pi/2,1)`

The maximum turning point on `y=2sinx` for `-pi<=x<=pi` is at `(pi/2,2)`

b. The straight line `y=kx` intersect the graph at the maximum point `(pi/2,2)`

Substitute `(pi/2,2)` into `y=kx`

`2=kxxpi/2`

`k=4/pi`

c. The straight line `y=4/pix` intersects the graph at `(-pi/2,-2)` using symmetry 

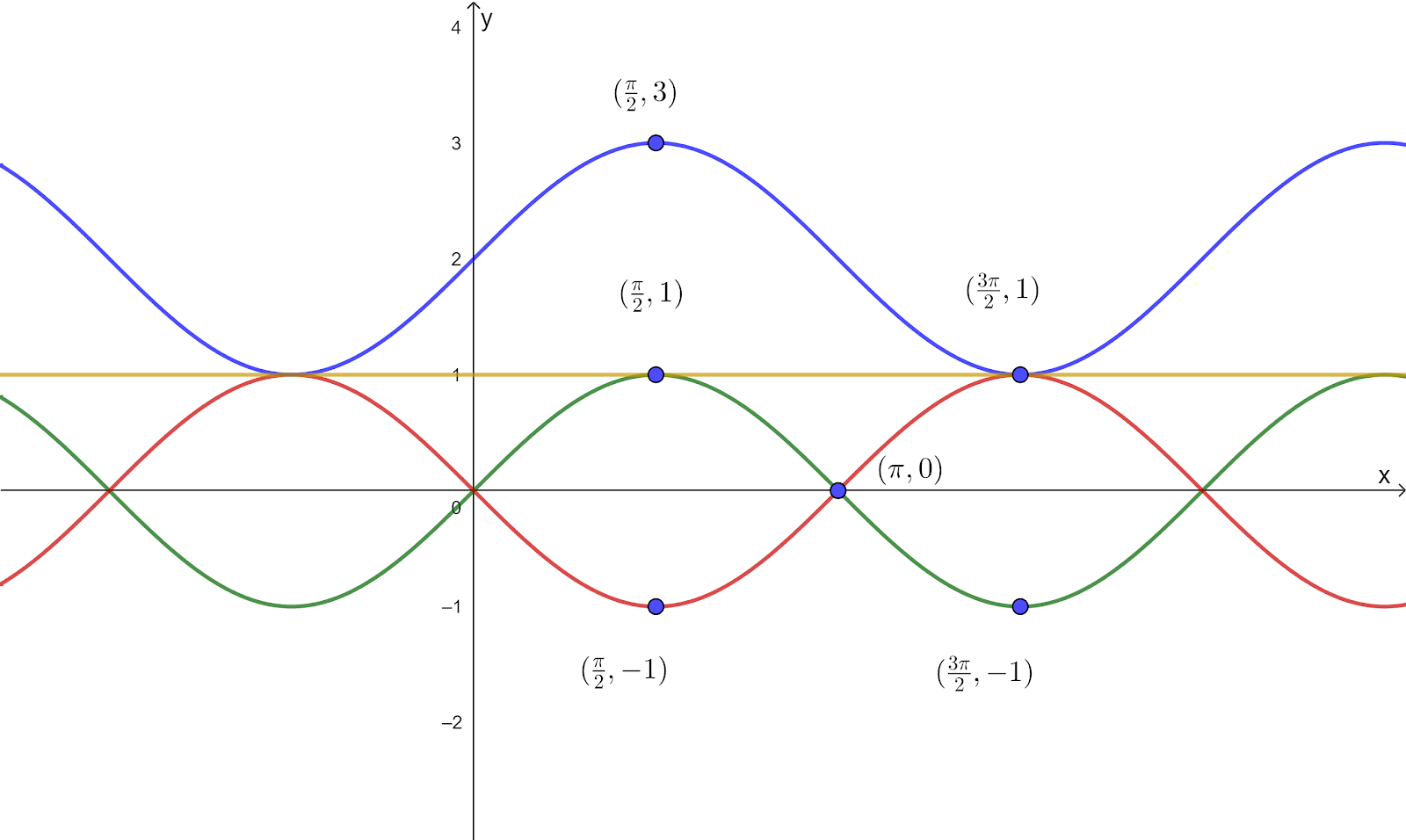
The graph of `y=sinx` is reflected in the line `x=pi` and then in the line `y=1`. 

Find the equation of the resulting function.

For `y=sinx` reflected in `x=pi`

Equation of the resulting function

`y=-sinx`

For `y=-sinx` reflected in `y=1`

Equation of the resulting function

`y=2+sinx`

The function `f(x)=5-2sinx` is defined for the domain `pi/2<=x<=p`.

a. Find the largest value of `p` for which `f` has an inverse.

b. For this value of `p`, find `f^-1(x)` and state the domain of `f^-1`.

a. The graph of `f(x)=sinx` is transformed to the graph of `f(x)=5-2sinx` by

+ a vertical stretch factor `2` (domain: `pi/2<=x<=p`, range: `-2<=x<=2`), followed by

+ a reflection in the x-axis (domain: `pi/2<=x<=p`, range: `-2<=x<=2`), followed by

+ a translation by the vector `((0),(5))` (domain: `pi/2<=x<=p`, range: `3<=f(x)<=7`)

For the domain `pi/2<=x`, the sketch of `f(x)=5-2sinx`

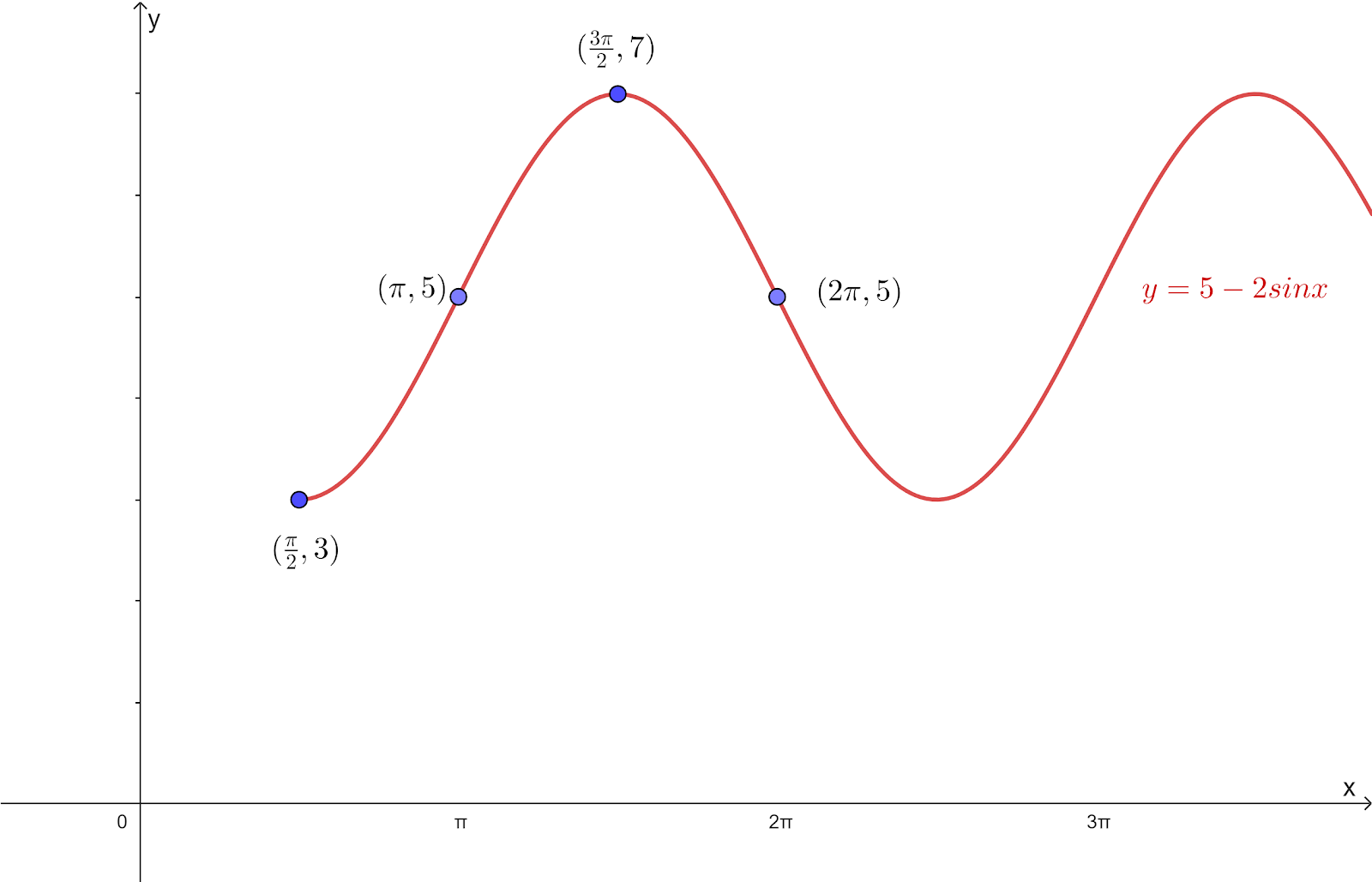
Function `f` has an inverse only if it is one to one

The maximum value of `x` from the graph is `frac{3pi}{2}`

Then `p = frac{3pi}{2}`

b. `f(x)=5-2sinx`

Write the function in terms of `y`

`y=5-2sinx`

Interchange the `x` and `y` variables

`x=5-2siny`

Rearrange to make `y` the subject

`2siny=5-x`

`siny=frac{5-x}{2}`

`y=sin^-1(frac{5-x}{2})`

Final solution

`f^-1(x)=sin^-1(frac{5-x}{2})`

The range of `f` is `3<=f(x)<=7` so the domain of `f^-1` is `3<=x<=7`

Solve each of these equations for the given domains:

a. `2tan(x/2)+sqrt3=0` for `0°<=x<=540°`.

b. `sqrt2sin(x/3+pi/4)=1` for `0 < x < 4pi`.

a. Let `A=x/2`

`2tanA+sqrt3=0`

`tanA=-sqrt3/2`

`A=tan^-1(-sqrt3/2)`

 `A=-40.89°`

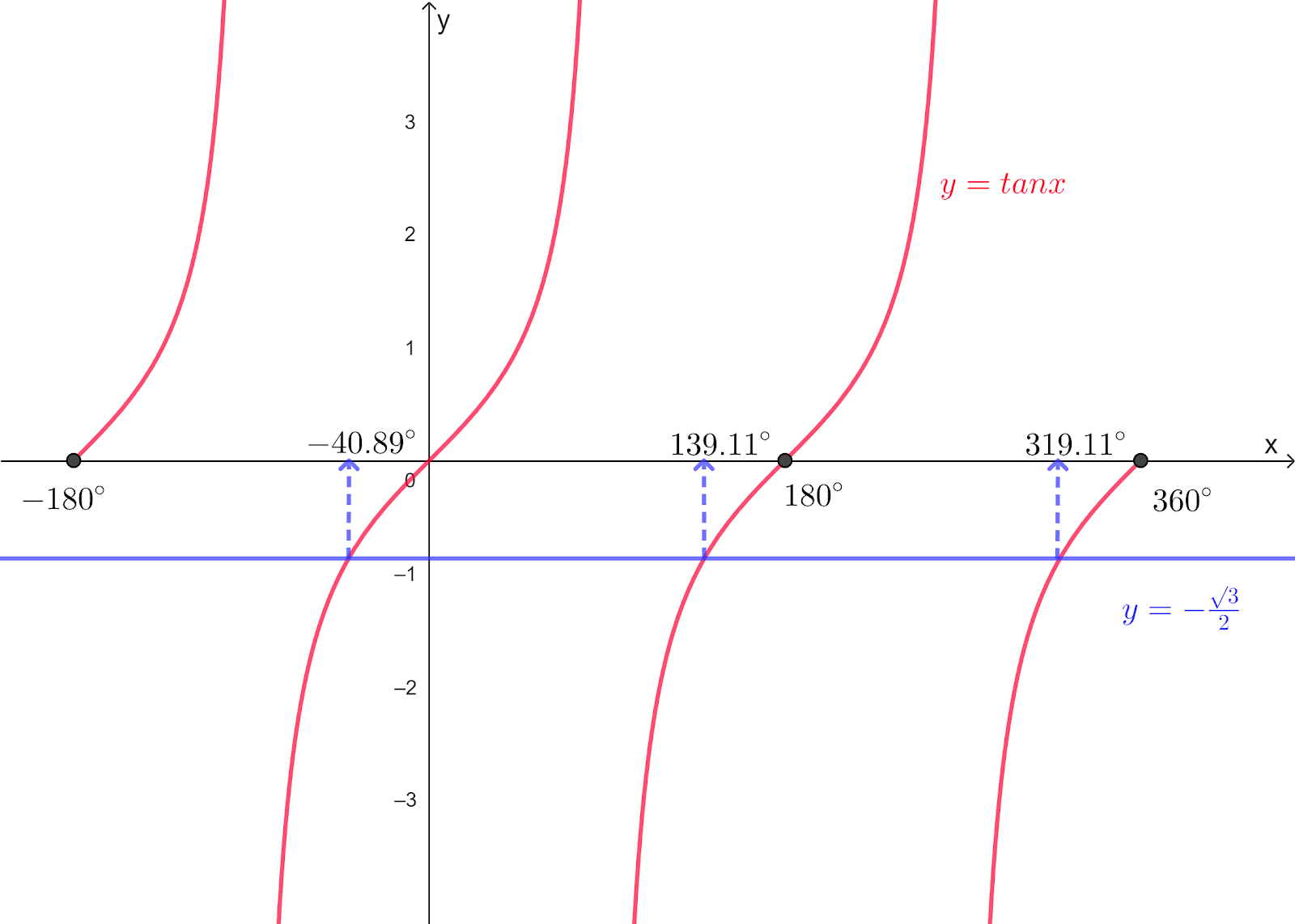
Using symmetry of the curve from the sketch

The first value

`180°-40.89°=139.11°`

The second value

`360°-40.89°=319.11°`

Substitute `139.11°` into `A=x/2`

`x=2A=2xx139.11°=278.22°`

Substitute `319.11°` into `A=x/2`

`x=2A=2xx319.11°=638.22°` (out of range `0°<=x<=540°`)

Then `x=278.2°` (correct to 1 decimal place)

b. Let `A=x/3+pi/4`

`sqrt2sinA=1`

`sinA=1/sqrt2`

`A=sin^-1(1/sqrt2)`

`A=pi/4` 

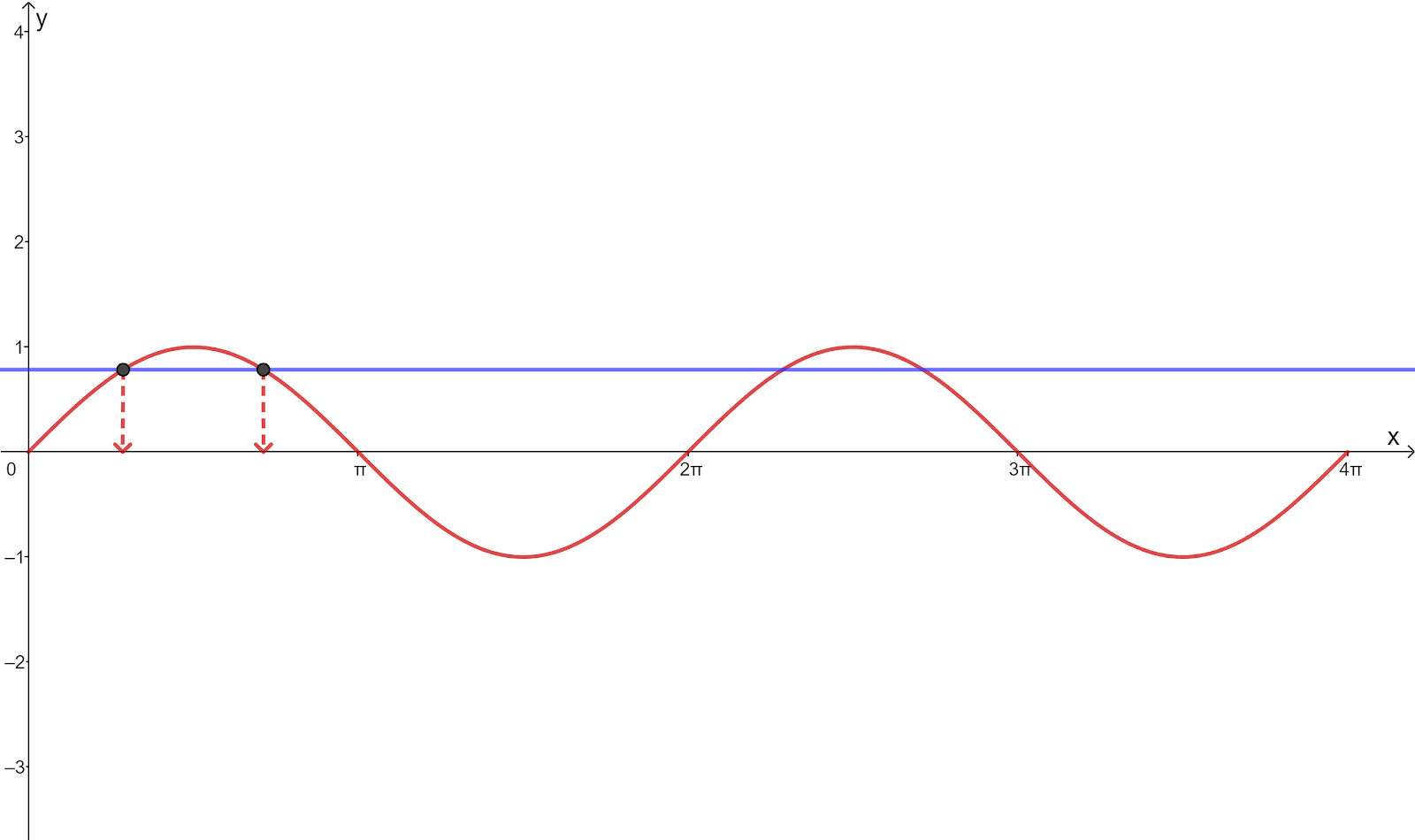
Using symmetry of the curve from the sketch

The first value

`0+pi/4=pi/4`

The second value

`pi-pi/4=frac{3pi}{4}`

Substitute `pi/4` into `A=x/3+pi/4`

`x/3=0`

`x=0` (out of range `0 < x < 4pi`)

Substitute `frac{3pi}[4}` into `A=x/3+pi/4`

`x/3=pi/2`

 `x=frac{3pi}{2}`

Then `x=frac{3pi}[2}`

Solve each of these equations for `0 <= x <= 2pi`

a. `4tanx=3cosx`

b. `2cos^2x+5sinx=4`

a. `4tanx=3cosx`

`4sinx/cosx=3cosx`

`4sinx=3cos^2x`

`4sinx=3(1-sin^2x)` (as `sin^2x+cos^2x=1`)

`4sinx=3-3sin^2x`

`3sin^2x+4sinx-3=0`

Let `y=sinx`

`3y^2+4y-3=0`

Using quadratic formula `y=frac{-b+-sqrt(b^2-4ac)}{2a}`

`y=frac{-4+-sqrt(4^2-4(3)(-3))}{2(3)}`

`y=frac{-4+-sqrt52}{6}`

`sinx=frac{-4+sqrt52}{6}` or `sinx=frac{-4-sqrt52}{6}`

`sinx=0.53518...` or `sinx=-1.8685`

Then `sinx=0.53518` (as `-1 <= sinx <=1`)

`x=0.5647` radians or `x=pi-0.5647=2.576` radians

b. `2cos^2x+5sinx=4`

`2(1-sin^2x)+5sinx=4` (as `sin^2x+cos^2x=1`)

`2-2sin^2x+5sinx-4=0`

`2sin^2x-5sinx+2=0`

`(2sinx-1)(sinx-2)=0`

`2sinx-1=0` or `sinx-2=0`

`sinx=1/2` or `sinx=2`

Then `sinx=1/2` (as `-1 <= sinx <= 1)`)

`x=pi/6` radians or `x=pi-pi/6=frac{5pi}{6}` radians

a. Given that `a=frac{1-sintheta}{2costheta}`, show that `1/a=frac{2(1+sintheta)}{costheta}`.

b. Hence, find `sintheta` and `costheta` in terms of `a`.

a. `a=frac{1-sintheta}{2costheta}`

Multiply by `2costheta`

`a(2costheta)=1-sintheta`

Divide by `a`

`2costheta=frac{1-sintheta}{a}`

Divide by `1-sintheta`

`frac{2costheta}{1-sintheta}=1/a`

Multiply the left-hand side by `1+sintheta`

`frac{2costheta(1+sintheta)}{(1-sintheta)(1+sintheta)}=1/a`

`frac{2costheta(1+sintheta)}{1-sin^2theta)=1/a` (as `(a+b)(a-b)=a^2-b^2`)

`frac{2costheta(1+sintheta)}{cos^2theta}=1/a` (as `sin^2theta+cos^2theta=1`)

Divide the left-hand side by `costheta`

`frac{2(1+sintheta)}{costheta}=1/a`

b. For `a(2costheta)=1-sintheta` (from part a)

`costheta=frac{1-sintheta}{2a}` (1)

For `1/a=frac{2(1+sintheta)}{costheta}`

`frac{costheta}{a}=2(1+sintheta)`

`costheta=2a(1+sintheta)` (2)

Solve (1) and (2)

`frac{1-sintheta}{2a}=2a(1+sintheta)`

`1-sintheta=2a(2a)(1+sintheta)`

`1-sintheta=4a^2+4a^2sintheta`

`1-4a^2=sintheta+4a^2sintheta`

`1-4a^2=sintheta(1+4a^2)`

`sintheta=frac{1-4a^2}{1+4a^2}`
For `a(2costheta)=1-sintheta` (from part a)

`sintheta=1-2acostheta` (3)

For (2)

`costheta=2a+2asintheta`

`costheta-2a=2asinntheta`

`sintheta=frac{costheta-2a}{2a}` (4)

Solve (3) and (4)

`1-2acostheta=frac{costheta-2a}{2a}`

`2a(1-2acostheta)=costheta-2a`

`2a-2a(2a)costheta=costheta-2a`

`2a+2a=costheta+4a^2costheta`

`4a=costheta(1+4a^2)`

`costheta=frac{4a}{1+4a^2}`

a. Show that the equation `sinthetatantheta=3` can be written in the form `cos^2theta+3costheta-1=0`.

b. Hence, solve the equation `sinthetatantheta=3` for `0° <= theta <= 360°`.

a. For `sinthetatantheta=3`

`sinthetaxxfrac{sintheta}{costheta}=3` (as `tantheta=sintheta/costheta`)

`sin^2theta/costheta=3`

`sin^2theta=3costheta`

`1-cos^2theta=3costheta` (as `sin^2theta+cos^2theta=1`)

`cos^2theta+3costheta-1=0`

b. Let `y=costheta`

`y^2+3y-1=0`

Using quadratic formula `y=frac{-b+-sqrt(b^2-4ac)}{2a}`

`y=frac{-3+-sqrt(3^2-4(1)(-1))}{2(1)}`

`y=frac{-3+-sqrt13}{2}`

`costheta=frac{-3+sqrt13}{2}` or `costheta=frac{-3-sqrt13}{2}`

`costheta=0.3027` or `costheta=-3.3027`

Then `costheta=0.3027` (as `-1 <= costheta <=1`)

`theta=72.4°` or `theta=360°-72.4°=287.6°`

a. Prove the identity `frac{1}{1+sintheta}+frac{1}{1-sintheta}-=frac{2}{cos^2theta}`.

b. Hence, solve the equation `costheta(frac{1}{1+sintheta}+frac{1}{1-sintheta})=5` for `0° <= theta <= 360°`.

a. For `frac{1}{1+sintheta}+frac{1}{1-sintheta}`

Multiply by `1-sintheta`

`=frac{1-sintheta}{(1+sintheta)(1-sintheta)}+frac{1+sintheta}{(1+sintheta)(1-sintheta)}`

`=frac{1-sintheta+1+sintheta}{(1+sintheta)(1-sintheta)`

`=frac{2}{1-sin^2theta}` (as `(a+b)(a-b)=a^2-b^2`)

`=frac{2}{cos^2theta}` (as `sin^2theta+cos^2theta=1`)

Then `frac{1}{1+sintheta}+frac{1}{1-sintheta}-=frac{2}{cos^2theta}`

b. `costheta(frac{1}{1+sintheta}+frac{1}{1-sintheta})=5`

`costhetaxx2/cos^2theta=5`

`2/costheta=5`

`2=5costheta`

`costheta=2/5`

`theta=66.4°` or `theta=360°-66.4°=293.6°`

a. Prove the identity `cos^4theta-sin^4theta-=2cos^2theta-1`.

b. Hence, solve the equation `cos^4theta-sin^4theta=1/2` for `0° <= theta <= 360°`.

a. For `cos^4theta-sin^4theta`

`=(cos^2theta-2sin^2theta)(cos^2theta+sin^2theta)` (as `(a+b)(a-b)=a^2-b^2`)

`=cos^2theta-sin^2theta` (as `sin^2theta+cos^2theta=1`)

`=cos^2theta-(1-cos^2theta)` 

`=cos^2theta-1+cos^2theta`

`=2cos^2theta-1`

Then `cos^4theta-sin^4theta-=2cos^2theta-1`

b. `2cos^2theta-1=1/2`

`2cos^2theta=3/2`

`cos^2theta=3/4`

`costheta=+-sqrt(3/4)`

`costheta=sqrt3/2` or `costheta=-sqrt3/2`

`theta=30°` or `theta=360°-30°=330°` or `theta=150°` or `theta=360°-150°=210°`

a. Show that the equation `frac{tanx+cosx}{tanx-cosx}=k`, where `k` is a constant, can be expressed as `(k+1)sin^2x+(k-1)sinx-(k+1)=0`.

b. Hence solve the equation `frac{tanx+cosx}{tanx-cosx}=4` for `0° <= x <= 360°`.

a. For `frac{tanx+cosx}{tanx-cosx}=k`

`frac{sinx/cosx+cosx}{sinx/cosx-cosx}=k` (as `tanx=sinx/cosx`)

`frac{frac{sinx+cos^2x}{cosx}}{frac{sinx-cos^2x}{cosx}}=k`

`frac{sinx+cos^2x}{sinx-cos^2x}=k`

`sinx+cos^2x=k(sinx-cos^2x)`

`sinx+1-sin^2x=k(sinx-(1-sin^2x))`

`sinx+1-sin^2x=ksinx-k+ksin^2x`

`ksin^2x+sin^2x+ksinx-sinx-k-1=0`

`(k+1)sin^2x+(k-1)sinx-(k+1)=0` (1)

b. `frac{tanx+cosx}{tanx-cosx}=4`

`k=4`

For (1)

`(4+1)sin^2x+(4-1)sinx-(4+1)=0`

`5sin^2x+3sinx-5=0`

Using quadratic formula `sinx=frac{-b+-sqrt(b^2-4ac)}{2a}`

`sinx=frac{-3+-sqrt(3^2-4(5)(-5))}{2(5)}`

`sinx=frac{-3+-sqrt109){10}`

`sinx=0.744` or `sinx=-1.344`

Then `sinx=0.744` (as `-1 <= sinx <=1`)

`x=48.1°` or `x=180°-48.1°=131.9°`

a. Prove the identity `frac{1+sinx}{1-sinx}-frac{1-sinx}{1+sinx}-=frac{4tanx}{cosx}`.

b. Hence solve the equation `frac{1+sinx}{1-sinx}-frac{1-sinx}{1+sinx}=8tanx` for `0 <= x <= 1/2 pi`.

a. For `frac{1+sinx}{1-sinx}-frac{1-sinx}{1+sinx}`

`=frac{(1+sinx)(1+sinx)}{(1-sinx)(1+sinx)}-frac{(1-sinx)(1-sinx)}{(1-sinx)(1+sinx)}`

`=frac{(1+sinx)^2-(1-sinx)^2}{(1-sinx)(1+sinx)`

`=frac{1+2sinx+sin^2x-(1-2sinx+sin^2x)}{1-sin^2x}` (as `(a+b)(a-b)=a^2-b^2`)

`=frac{1+2sinx+sin^2x-1+2sinx-sin^2x}{1-sin^2x}`

`frac{4sinx}{1-sin^2x}`

`=frac{4sinx}{cos^2x}` (as `sin^2x+cos^2x=1`)

`=frac{4sinx}{cosxcosx}`

`=frac{4tanx}{cosx}` (as `tanx=sinx/cosx`)

Then `frac{1+sinx}{1-sinx}-frac{1-sinx}{1+sinx}-=frac{4tanx}{cosx}`

b. `frac{4tanx}{cosx}=8tanx`

`frac{4tanx}{cosx}-8tanx=0`

`4tanx(1/cosx-2)=0`

`4tanx=0` or `1/cosx-2=0`

`tanx=0` or `1/cosx=2`

`tanx=0` or `cosx=1/2`

`x=0` or `x=pi/3`

a. Prove the identity `frac{1-2sin^2theta}{1-sin^2theta}-=1-tan^2theta`.

b. Hence solve the equation `frac{1-2sin^2theta}{1-sin^2theta}=2tan^4theta` for `0° <= theta <= 180°`.

a. For `frac{1-2sin^2theta}{1-sin^2theta}`

`=frac{1-sin^2theta-sin^2theta}{cos^2theta}` (as `sin^2theta+cos^2theta=1`)

`=frac{cos^2theta-sin^2theta}{cos^2theta}`

`=cos^2theta/cos^2theta-sin^2theta/cos^2theta`

`1-tan^2theta` (as `tantheta=sintheta/costheta`)

Then `frac{1-2sin^2theta}{1-sin^2theta}-=1-tan^2theta`

b. `1-tan^2theta=2tan^4theta`

`2tan^4theta+tan^2theta-1=0`

Using quadratic formula `tan^2theta=frac{-b+-sqrt(b^2-4ac)}{2a}`

`tan^2theta=frac{-1+-sqrt(1^2-4(2)(-1))}{2(2)}`

`tan^2theta=frac{-1+-3}{4}`

`tan^2theta=0.5` or `tan^2theta=-1`

Then `tantheta=+-sqrt0.5`

`theta=35.3°` or `theta=180°-35.3°=144.7°`

a. Show that `frac{sintheta+2costheta}{costheta-2sintheta}-frac{sintheta-2costheta}{costheta+2sintheta}=frac{4}{5cos^2theta-4}`.

b. Hence solve the equation `frac{sintheta+2costheta}{costheta-2sintheta}-frac{sintheta-2costheta}{costheta+2sintheta}=5` for `0° < theta < 180°`.

a. For `frac{sintheta+2costheta}{costheta-2sintheta}-frac{sintheta-2costheta}{costheta+2sintheta}`

`=frac{(sintheta+2costheta)(costheta+2sintheta)}{(costheta-2sintheta)(costheta+2sintheta)}-frac{(sintheta-2costheta)(costheta-2sintheta)}{(costheta-2sintheta)(costheta+2sintheta)}`

`=frac{sinthetacostheta+2sin^2theta+2cos^2theta+4sinthetacostheta}{cos^2theta-4sin^2theta}-frac{sinthetacostheta-2sin^2theta-2cos^2theta+4sinthetacostheta}{cos^2theta-4sin^2theta}` 

(as `(a+b)(a-b)=a^2-b^2`)

`=frac{5sinthetacostheta+2sin^2theta+2cos^2theta-(5sinthetacostheta-2sin^2theta-2cos^2theta)}{cos^2theta-4sin^2theta}`

`=frac{5sinthetacostheta+2sin^2theta+2cos^2theta-5sinthetacostheta+2sin^2theta+2cos^2theta}{cos^2theta-4sin^2theta}`

`=frac{4sin^2theta+4cos^2theta}{cos^2theta-4sin^2theta}`

`=frac{4(sin^2theta+cos^2theta)}{cos^2theta-4(1-cos^2theta)}` (as `sin^2theta+cos^2theta=1`)

`=frac{4(1)}{cos^2theta-4+4cos^2theta}`

`=frac{4}{5cos^2theta-4}`

Then `frac{sintheta+2costheta}{costheta-2sintheta}-frac{sintheta-2costheta}{costheta+2sintheta}=frac{4}{5cos^2theta-4}`

b. `frac{4}{5cos^2theta-4}=5`

`4=5(5cos^2theta-4)`

`4=25cos^2theta-20`

`24=25cos^2theta`

`cos^2theta=24/25`

`costheta=+-sqrt(24/25)`

`costheta=+-0.9798`

`theta=11.5°` or `theta=180°-11.5°=168.5°`

a. Prove the identity `frac{sin^3theta}{sintheta-1}-frac{sin^2theta}{1+sintheta}-=-tan^2theta(1+sin^2theta)`.

b. Hence solve the equation `frac{sin^3theta}{sintheta-1}-frac{sin^2theta}{1+sintheta}=tan^2theta(1-sin^2theta)` for `0 < theta < 2pi`.

a. For `frac{sin^3theta}{sintheta-1}-frac{sin^2theta}{1+sintheta}`

`=frac{sin^3theta(sintheta+1)}{(sintheta-1)(sintheta+1)}-frac{sin^2theta(sintheta-1)}{(1+sintheta)(sintheta-1)}`

`=frac{sin^4theta+sin^3theta}{(sintheta-1)(sintheta+1)}-frac{sin^3theta-sin^2theta}{(sintheta-1)(sintheta+1)}`

`=frac{sin^4theta+sin^3theta-(sin^3theta-sin^2theta)}{sin^2theta-1}` (as `(a+b)(a-b)=a^2-b^2`)

`=-frac{sin^4theta+sin^3theta-sin^3theta+sin^2theta}{1-sin^2theta}`

`=-frac{sin^2theta(1+sin^2theta)}{cos^2theta}` (as `sin^2theta+cos^2theta=1`)

`=-tan^2theta(1+sin^2theta)` (as `tantheta=sintheta/costheta`)

Then `frac{sin^3theta}{sintheta-1}-frac{sin^2theta}{1+sintheta}-=-tan^2theta(1+sin^2theta)`

b. `-tan^2theta(1+sin^2theta)=tan^2theta(1-sin^2theta)`

`tan^2theta(1-sin^2theta)+tan^2theta(1+sin^2theta)=0`

`tan^2theta(1-sin^2theta+1+sin^2theta)=0`

`tan^2thetaxx2=0`

`tan^2theta=0`

`tantheta=0`

`theta=pi`

a. (i) By first expanding `(costheta+sintheta)^2`, find the three solutions of the equation `(costheta+sintheta)^2=1` for `0 <= theta <= pi`.

(ii) Hence verify that the only solutions of the equation `costheta+sintheta=1` for are `0` and for `1/2pi`.

b. Prove the identity `frac{sintheta}{costheta+sintheta}+frac{1-costheta}{costheta-sintheta}-=frac{costheta+sintheta-1}{1-2sin^2theta}`.

c. Using the results of (a) (ii) and (b), solve the equation `frac{sintheta}{costheta+sintheta}+frac{1-costheta}{costheta-sintheta}=2(costheta+sintheta-1)` for `0 <= theta <= pi`.

a. (i) For `(costheta+sintheta)^2=1`

`cos^2theta+sin^2theta+2costhetasintheta=1`

`1+2costhetasintheta=1` (as `sin^2theta+cos^2theta=1`)

`2costhetasintheta=0` 

`costheta=0` or `sintheta=0`

`theta=pi/2` or `theta=-pi/2` or `theta=frac{3pi}{2}` or `theta=0` or `theta=pi`

Then `theta=pi/2` or `theta=0` or `theta=pi`

(ii) For `theta=0`

`cos0+sin0=1+0=1`

For `theta=pi/2`

`cos frac{pi}{2} +sin frac{pi}{2} =0+1=1`

For `theta=pi`

`cospi+sinpi=-1+0=-1`

Then `costheta+sintheta=1` when `theta=0` and `theta=pi/2`

b. For `frac{sintheta}{costheta+sintheta}+frac{1-costheta}{costheta-sintheta}`

`=frac{sintheta(costheta-sintheta)}{(costheta+sintheta)(costheta-sintheta)}+frac{(1-costheta)(costheta+sintheta)}{(costheta+sintheta)(costheta-sintheta)}`

`frac{sinthetacostheta-sin^2theta+costheta+sintheta-cos^2theta-sinthetacostheta}{(costheta+sintheta)(costheta-sintheta)}`

`=frac{costheta+sintheta-sin^2theta-cos^2theta}{cos^2theta-sinthetacostheta+sinthetacostheta-sin^2theta}`

`=frac{costheta+sintheta-(sin^2theta+cos^2theta)}{cos^2theta-sin^2theta}`

`=frac{costheta+sintheta-1}{1-sin^2theta-sin^2theta` (as `sin^2theta+cos^2theta=1`)

`=frac{costheta+sintheta-1}{1-2sin^2theta}`

Then `frac{sintheta}{costheta+sintheta}+frac{1-costheta}{costheta-sintheta}-=frac{costheta+sintheta-1}{1-2sin^2theta}`

c. `frac[costheta+sintheta-1}{1-2sin^2theta}=2(costheta+sintheta-1)`

`costheta+sintheta-1=2(costheta+sintheta-1)(1-2sin^2theta)` 

`costheta+sintheta-1-2(costheta+sintheta-1)(1-2sin^2theta)=0`

`(costheta+sintheta-1)[(1-2(1-2sin^2theta)]=0`

`(costheta+sintheta-1)(1-2+4sin^2theta)=0`

`(costheta+sintheta-1)(4sin^2theta-1)=0`

`costheta+sintheta-1=0` or `4sin^2theta-1=0`

`costheta+sintheta=1` or `4sin^2theta=1`

`theta=0` or `theta=pi/2` (part a) or `sin^2theta=1/4`

`theta=0` or `theta=pi/2` or `sintheta=1/2` or `sintheta=-1/2`

`theta=0` or `theta=pi/2` or `theta=pi/6` or `theta=frac{5pi}[6}` or `theta=-pi/6` or `theta=frac{7pi}{6}`

Then `theta=0` or `theta=pi/2` or `theta=pi/6` or `theta=frac{5pi}{6}`