Series

Use Pascal’s triangle to find the expansions of:

a. `(2x+3y)^3`

b. `(2x-3)^4`

a. The index is 3 so use the row for n = 3 in Pascal’s triangle: (1, 3, 3, 1)

`(2x+3y)^3`

`=1(2x)^3+3(2x)^2(3y)+3(2x)(3y)^2+1(3y)^3`

`=8x^3+36x^2y+54xy^2+27y^3`

b. The index is 4 so use the row for n = 4 in Pascal’s triangle: (1, 4, 6, 4, 1)

`(2x-3)^4`

`=1(2x)^4+4(2x)^3(-3)+6(2x)^2(-3)^2+4(2x)(-3)^3+1(-3)^4`

`=16x^4-96x^3+216x^2-216x+81`

`(3+x)^5+(3-x)^5-=A+Bx^2+Cx^4`

Find the value of A, the value of B and the value of C.

The index is 5 so use the row for n = 5 in Pascal’s triangle: (1, 5, 10, 10, 5, 1) 

For `(3+x)^5`

`=1(3)^5+5(3)^4(x)+10(3)^3(x)^2+10(3)^2(x)^3+5(3)(x)^4+1(x)^5`

`=243+405x+270x^2+90x^3+15x^4+x^5`

For `(3-x)^5`

`=1(3)^5+5(3)^4(-x)+10(3)^3(-x)^2+10(3)^2(-x)^3+5(3)(-x)^4+1(-x)^5`

`=243-405x+270x^2-90x^3+15x^4-x^5`

For `(3+x)^5+(3-x)^5`

`=243+405x+270x^2+90x^3+15x^4+x^5+243-405x+270x^2-90x^3+15x^4-x^5`

`=486+540x^2+30x^4`

Then `A = 486`, `B = 540`, `C = 30`

The coefficient of `x^2` in the expansion of `(1+ax)^4` is 30 times the coefficient of in the expansion of `(1+frac{ax}{3})^3`. Find the value of `a`.

The index is 4 so use the row for n = 4 in Pascal’s triangle: (1, 4, 6, 4, 1)

`(1+ax)^4`

 `=1(1)^4+4(1)^3(ax)+6(1)^2(ax)^2+4(1)(ax)^3+1(ax)^4`

The term in `x^2` is `6(1)^2(ax)^2` or `6a^2x^2`

The index is 3 so use the row for n = 3 in Pascal’s triangle: (1, 3, 3, 1)

`(1+frac{ax}{3})^3`

`=1(1)^3+3(1)^2(frac{ax}{3})+3(1)(frac{ax}{3})^2+1(frac{ax}{3})^3`

The term in `x` is `3(1)^2(frac{ax}{3})` or `ax`

For `6a^2=30xxa`

`a=5`

Use the formula `((n),(r))=frac{n!}{r!(n-r)!}` to find the value of each of the following:

a. `((14),(3))`

b. `((12),(7))`

a. `((14),(3))=frac{14!}{3!(14-3)!}=frac{14!}{3!11!}=364`

b. `((12),(7))=frac{12!}{7!(12-7)!}=frac{12!}{7!5!}=792`

a. Find, in ascending powers of x, the first three terms of in the expansion of `(2+x)^10`.

b. By replacing `x` with `2y-3y^2`, find the first three terms in the expansion of `(2+2y-3y^2)^10`.

a. For `(2+x)^10`

`=((10),(0))2^10+((10),(1))2^9(x)^1+((10),(2))2^8(x)^2+...`

`=1024+5120x+11520x^2+...`

b. For `(2+2y-3y^2)^10`

`1024+5120(2y-3y^2)+11520((2y-3y^2)^2+...`

`=1024+10240y-15360y^2+46080y^2+...`

`=1024+10240y+30720y^2+...` 

In an arithmetic progression, the first term is `-27`, the 16^th term is `78` and the last term is `169`.

a. Find the common difference and the number of terms.

b. Find the sum of the terms in this progression.

a. Use n^th term `= a + (n - 1)d`

`78 = -27 + (16 - 1)d`

`78 + 27 = 15d`

`d = 7`

Then the common difference is `7`

Use n^th term `= a + (n - 1)d`

`169 = -27 + (n - 1)7`

`169 + 27 = 7n - 7`

`203 = 7n`

`n = 29`

Then there are `29` terms

b. Use `S_n=n/2(a+l)`

`S_29=29/2(-27+169)`

`S_29=2059`

The first term of an arithmetic progression is `sin^2x` and the second term is `1`.

a. Write down an expression, in terms of `sinx`, for the fifth term of this progression.

b. Show that the sum of the first ten terms of this progression is `10+35cos^2x`.

a. Common difference is `1-sin^2x`

Then `1-sin^2x-=cos^2x` (as `sin^2x+cos^2x-=1`)

Use n^th term `= a + (n - 1)d`

The 5^th term 

`=sin^2x+(5-1)(1-sin^2x)`

`=sin^2x+4-4sin^2x`

`=4-3sin^2x`

b. Use `S_n=n/2[2a+(n-1)d]`

`S_10=10/2[2sin^2x+(10-1)(1-sin^2x)]`

`S_10=5(2sin^2x+9-9sin^2x)`

`S_10=5(9-7sin^2x)`

`S_10=45-35sin^2x`

`S_10=45-35(1-cos^2x)` (as `sin^2x+cos^2-=1`)

 `S_10=45-35+35cos^2x`

 `S_10=10+35cos^2x`

A ball is thrown vertically upwards from the ground. The ball rises to a hight of `8` m and then falls and bounces. After each bounce it rises to `3/4` of the height of the previous bounce.

a. Write down an expression for the height that the ball rises after the n^th impact with the ground.

b. Find the total distance that the ball travels from the first throw to the fifth impact with the ground.

a. Use geometric progression

The first term

`ar^(n-1)=axx(3/4)^0=8`

Then `a=8`

The second term 

`ar^(n-1)=8xx(3/4)^1=6`

After the n^th impact, the ball rises `8xx(3/4)^(n-1)`

b. 

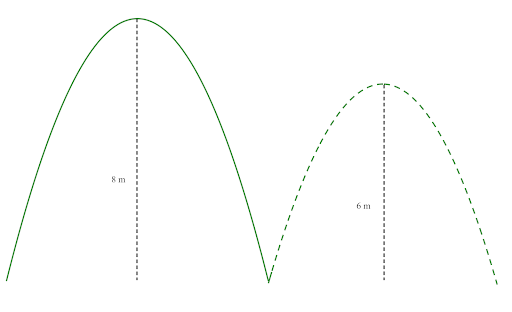
The distance that the ball travels at the first impact

`8xx2=16` m

The total distance that the ball travels

`S_n=frac{a(1-r^n)}{1-r}xx2` (as `-1)

`S_5=frac{8[1-(3/4)^5]}{1-3/4}xx2=48.8125` m

A company makes a donation to charity each year. The value of the donation increases exponentially by `10%` each year. The value of the donation in 2010 was `$"10 000"`.

a. Find the value of the donation in 2016.

b. Find the total value of the donations made during the years 2010 to 2016, inclusive.

a. Let `r = 100% + 10% = 1.1`, `a = 10000`, `n = 2016 - 2010 +1 = 7`

The value of the donation in 2016

`ar^(n-1)=10000xx(1.1)^(7-1)=$17715.61`

b. 2010 to 2016 inclusive `= 7` years

The total value of the donations

`S_n=frac{a(r^n-1)}{r-1}` (as `r>1`)

`S_7=frac{10000(1.1^7-1)}{1.1-1}=$94871.71`

The third term of a geometric progression is `16` and the sixth terms is `-1/4`.

a. Find the common ratio and the first term.

b. Find the sum to infinity.

a. The third term 

`ar^(n-1)=ar^2=16` (1)

The sixth term 

`ar^(n-1)=ar^5=-1/4`

Common ratio

`frac{ar^5}{ar^2}=frac{-1/4}{16}`

`r^3=-1/64`

`r=-1/4`

The first term

Substitute `r=-1/4` into (1)

`a(-1/4)^2=16`

`1/16a=16`

`a=256`

b. The sum to infinity

`S_∞=frac{a}{1-r}=frac{256}{1-(-1/4)}=204.8`

The first term of a geometric progression is `1` and the second term is `2cosx`, where `0. Find the set of values of `x`  for which this progression is convergent.

The first term `a = 1`, the second term `ar=2cosx`

The progression is convergent when `|r|<1` or `-1

Common ratio

`frac{ar}{a}=frac{2cosx}{1}`

`r=2cosx`

So `-1<2cosx<1`

`-1/2

`0 < cosx < 1/2` (as `0 < x < pi/2`, cos is positive in this domain)

Then `pi/3 < x < pi/2`

The first term of an arithmetic progression is `16` and the sum of the first `20` terms is `1080`. 

a. Find the common difference of this progression. The first, third and n^th terms of this arithmetic progression are the first, second and third terms, respectively, of a geometric progression. 

b. Find the common ratio of the geometric progression and the value of `n`.

a. Let `a=16`, `S_20=1080`

The common difference

`S_n=n/2[2a+(n-1)d]`

`1080=20/2[2xx16+(20-1)d]`

`108=32+19d`

`19d=76`

`d=4`

b. For the geometric progression

The first term is `a = 16`, the second term is `16r`, the third term is `16r^2` (1)

For the arithmetic progression

The first term is `16`, the third term is `16+2xx4=24`, the nth term is `16+(n-1)xx4=16+4n-4=12+4n` (2)

From (1) and (2)

The common ratio `r`

`24=16r`

`r=1.5`

The value of `n` 

`12+4n=16r^2`

`12+4n=16xx1.5^2`

`12+4n=36`

`4n=24`

`n=4`

a. A geometric progression has a second term of `12` and a sum to infinity of `54`. Find the possible values of the first term of the progression.

b. The `n^(th)` term of a progression is `p + qn`, where `p` and `q` are constants, and `S_n` is the sum of the first `n` terms.

(i) Find an expression, in terms of `p`, `q` and `n`, for `S_n`.

(ii) Given that `S_4=40` and `S_6=72`, find the values of `p` and `q`.

a. The second term

`ar=12`

`a=12/r`

The sum to infinity

`S_∞=frac{a}{1-r}=54`

Substitute `a=12/r`

`frac{12/r}{1-r}=54`

`12/r=54(1-r)`

`12=54r-54r^2` 

`-9r^2+9r-2=0`

`(-3r+1)(3r-2)=0`

`r=1/3` or `r=2/3`

 `a=frac{12}{1/3}=36` or `a=frac{12}{2/3}=18`

Then the first term `a=36` or `a=18`

b. (i) The first term is `p + q`

The `n^(th)` term is `p + qn`

The common difference is `q`

The sum of the term

`S_n=n/2[2(p+q)+(n-1)q]` 

`S_n=n/2(2p+q+qn)` (1)

(ii) From (1)

`S_4=4/2(2p+q+qxx4)=40` 

 `4p+10q=40`(2)

`S_6=6/2(2p+q+qxx6)=72`

`6p+21q=72` (3)

From (2)

`4p=40-10q`

`p=10-5/2q`

Substitute `p=10-5/2q` into (3)

`6(10-5/2q)+21q=72`

`60-15q+21q=72`

`6q=12` 

`q=2`

Then `p=10-5/2(2)=5`

The coefficient of `x^2` in the expression of `(4+ax)(1+x/2)^6` is `3`. Find the value of the constant `a`.

Use binomial expansion on `(1+x/2)^6`

`=((6),(0))1^6(x/2)^0+((6),(1))1^5(x/2)^1+((6),(2))1^4(x/2)^2+...`

`=1+3x+frac{15x^2}{4}+...` 

For `(4+ax)(1+x/2)^6`

`=4(1+x/2)^6+ax(1+x/2)^6`

`=4(1+3x+frac{15x^2}{4}+...)+ax(1+3x+frac{15x^2}{4}+...)`

`(4+12x+15x^2+...)+(ax+3ax^2+frac{15ax^3}{4}+...)`

The coefficient of `x^2` is `15+3a=3`

`3a=-12` 

 `a=-4`

Two heavyweight boxers decide that they would be more successful if they competed in a lower weight class. For each boxer this would require a total weight loss of `13` kg. At the end of week `1` they have each recorded a weight loss of `1` kg and they both find that in each of the following weeks their weight loss is slightly less than the week before. 

Boxer A’s weight loss in week `2` is `0.98` kg. It is given that his weekly weight loss follows an arithmetic progression.

(i) Write down an expression for his total weight loss after `x` weeks.

(ii) He reaches his `13` kg target during week `n`. Use your answer to part (i) to find the value of `n`.

(iii) Boxer B’s weight loss in week `2` is `0.92` kg and it is given that his weekly weight loss follows a geometric progression.

Calculate his total weight loss after `20` weeks and show that he can never reach his target.

(i) The common difference of weight loss

`0.98 - 1 = -0.02`

Let `a=1`, `d= –0.02`

The total weight loss after `x` weeks using arithmetic progression

`S_n=n/2[2a+(n-1)d]`

`S_x=x/2[2(1)+(x-1)(-0.02)]` 

`=x/2[2-0.02(x-1)]` 

`=x(1-0.01x+0.01)` 

`=1.01x-0.01x^2` 

(ii) For `S_n=13=1.01n-0.01n^2`

`0.01n^2-1.01n+13=0` 

Using quadratic formula `n=frac{-b+-sqrt(b^2-4ac)}{2a}`

`n=frac{-(-1.01)+-sqrt((-1.01)^2-4(0.01)(13))}{2(0.01)}` 

`n=frac{1.01+-sqrt(0.5001)}{0.02}` 

`n=85.9` or `n=15.1`

Then `n=16` weeks

(iii) Let `a = 1`, `r = 0.92`, `n = 20`

The total weight loss after `20` weeks using geometric progression

`S_n=frac{a(1-r^n)}{1-r}` (as `-1)

`=frac{1(1-0.92^20)}{1-0.92}` 

`=10.1` 

The sum to infinity

`S_∞=frac{a}{1-r}=frac{1}{1-0.92}=12.5` 

Then he can never reach his target (as `12.5 < 13`)

The first and second terms of an arithmetic progression are `1/cos^2theta` and `-tan^2theta/cos^2theta` respectively, where `0.

a. Show that the common difference is `-1/cos^4theta`.

b. Find the exact value of the 13^th term when `theta=1/6pi`.

a. The common difference

`-tan^2theta/cos^2theta-1/cos^2theta`

`=-frac{sin^2theta/cos^2theta}{cos^2}-1/cos^2theta` (as `tantheta=sintheta/costheta`)

`=-sin^2theta/cos^4theta-cos^2theta/cos^4theta` 

`=frac{-sin^2theta-cos^2theta}{cos^4theta}` 

`=-1/cos^4theta` (as `sin^2theta+cos^2theta=1`)

b. The first term

`a=1/cos^2theta=1/((cosfrac(pi)(6))^4)=1/((sqrt3/2)^4)=-16/9` 

The common difference

`d=-1/cos^4theta=-1/((cosfrac(pi)(6))^4)=-1/(sqrt3/2)^4=-16/9` 

The 13^th term

`a+12d=4/3+12xx(-16/9)=-20` 

A woman’s basic salary for her first year with a particular company is $`30 000` and at the end of the year she also gets a bonus of $`600`. 

a. For her first year, express her bonus as a percentage of her basic salary.

b. At the end of each complete year, the woman’s basic salary will increase by `3%` and her bonus will increase by $`100`.

Express the bonus she will be paid at the end of her 24^th year as a percentage of the basic salary paid during that year.

a. Her bonus for the first year

`600/30000xx100%=2%` 

b. Her bonus 

`a+(n-1)d=600+(23)(100)=2900` 

Her basic salary

`r=100%+3%=103%=1.03` 

`ar^(n-1)=30000xx(1.03)^23=59207.60` 

Her bonus at the end of her 24^th year

`2900/59207.60xx100%=4.90%` 

a. A geometric progression is such that the second term is equal to `24%` of the sum to infinity. Find the possible values of the common ratio.

b. An arithmetic progression `P` has first term `a` and common difference `d`. An arithmetic progression `Q` has first term `2(a + 1)` and common difference `(d + 1)`. It is given that `frac{"5th term of P"}{"12th term of Q"}=1/3` and `frac{"Sum of first 5 terms of P"}{"Sum of first 5 term of Q"}=2/3`. Find the value of `a` and the value of `d`.

a. The second term 

`ar=24%xxS_∞` 

`ar=24/100xxfrac{a}{1-r}` 

`r=frac{24}{100-100r}` 

`100r-100r^2=24` 

`100r^2-100r+24=0` 

`25r^2-25r+6=0` 

`(5r-3)(5r-2)=0` 

`5r-3=0` or `5r-2=0`

`r=3/5` or `r=2/5`

b. The 5^th term of P

`a+4d` 

The 12^th term of Q

 `2(a+1)+11(d+1)=2a+11d+13`

The sum of first 5 terms of P

`5/2(2a+4d)=5a+10d` 

The sum of first 5 terms of Q

`5/2[2(2(a+1))+4(d+1)]=10a+10+10d+10=10a+10d+20` 

For `frac{"5th term of P"}{"12th term of Q"}=1/3`

`frac{a+4d}{2a+11d+13}=1/3` 

`3(a+4d)=2a+11d+13` 

`3a+12d=2a+11d+13` 

`a=-d+13` (1)

For `frac{"Sum of first 5 terms of P"}{"Sum of first 5 term of Q"}=2/3`

`frac{5a+10d}{10a+10d+20}=2/3` 

`3(5a+10d)=2(10a+10d+20)` 

`15a+30d=20a+20d+40`

`5a=10d-40` 

`a=2d-8` (2)

From (1) and (2)

`-d+13=2d-8` 

`3d=21` 

`d=7` 

Substitute `d=7` into (1)

`a=-7+13=6` 

The coefficient of `x^2` in the expansion of `(1+2/px)^5+(1+px)^6` is `70`. Find the possible values of the constant `p`.

In binomial expansion of `(1+2/px)^5`

`((5),(2))1^3(2/px)^2=10(4/p^2)x^2` 

In binomial expansion of `(1+px)^6`

`((6),(2))1^4(p)^2=15p^2` 

The coefficient of `x^2`

`10(4/p^2)+15p^2=70` 

`40/p^2+15p^2=70` 

`40+15p^4=70p^2` 

`3p^4-14p^2+8=0` 

`(p^2-4)(3p^2-2)=0` 

`p^2-4=0` or `3p^2-2=0`

`p^2=4` or `p^2=2/3`

`p=+-2` or `p=+-sqrt(2/3)`

The coefficient of `x^4` in the expansion of `(x+a)^6` is `p` and the coefficient `x^2` of in the expansion of `(ax+3)^4` is `q`. It is given that `p+q=276`. Find the possible values of the constant `a`.

In binomial expansion of `(a+x)^6`

`((6),(4))a^2x^4=15a^2x^4` 

In binomial expansion of `(ax+3)^4`

`((4),(2))(ax)^2 3^2=54a^2x^2` 

For `p+q=276`

`15a^2+54a^2=276` 

`69a^2=276` 

`a^2=4` 

`a=+-2`