A Level Mathematics - Questionbank
Differentiation focuses on finding derivatives of functions using basic rules, including the power rule and sum rule. Students learn to apply differentiation to solve problems involving tangents, normals, rates of change, and stationary points. This topic is essential for understanding calculus and its applications in optimization and motion analysis.
Question 1
Find the gradient of the curve at the point where the curve `y=frac{5x-10}{x^2}` crosses the x-axis.
Easy
Mark as Complete
Mark Scheme
Question 2
Given that `y=2x^3 - 3x^2-36x+5`, find the range of values of `x` for which `frac{dy}{dx} < 0` .
Medium
Mark as Complete
Mark Scheme
Question 3
Differentiate with respect to `x`:
`a. frac{7}{(2x^2-5x)^7}`
`b. frac{6}{root(3)(2-3x)}`
Easy
Mark as Complete
Mark Scheme
Question 4
Find the coordinates of the point on the curve `y=sqrt ((x^2-10x+26))` where the gradient is `0`.
Easy
Mark as Complete
Mark Scheme
Question 5
The normal to the curve `y=x^3 -5x+3` at the point `(-1,7)` intersects the y-axis at the point P. Find the coordinates of P.
Easy
Mark as Complete
Mark Scheme
Question 6
The normal to the curve `y = x^3 - 5x + 3` at the point `(-1, 7)` intersects the y-axis at the point P.
Find the coordinates of `P`.
Easy
Mark as Complete
Mark Scheme
Question 7
The curve `y= 2x^2 +kx -3` at the point `(3,-6)` is parallel to the line `x+5y=10` .
a. Find the value of `k`.
b. Find the coordinates of the point where the normal meets the curve again.
Medium
Mark as Complete
Mark Scheme
Question 8
Given that `f(x)= frac{2}{sqrt(1-2x)}` , find the value of `f''(-4)`
Easy
Mark as Complete
Mark Scheme
Question 9
Given that `y=x^2-2x+5` , show that `4frac{d^2y}{dx^2}+(x-1)frac{dy}{dx}=2y`
Easy
Mark as Complete
Mark Scheme
Question 10
A curve has equation `y=x^3+2x^2-4x+6` .
a. Show that `frac{dy}{dx}=0` when `x=-2` and when `x=2/3` .
b. Find the value of `frac{d^2y}{dx^2}` when `x=-2` and when `x=2/3` .
Easy
Mark as Complete
Mark Scheme
Question 11
A curve has equation `y=frac{ax+b}{x^2}` . Given that `frac{ dy}{dx}=0` and `frac{d^2y}{dx^2}=1/2` when `x=2` , find the value of a and the value of `b`.
Medium
Mark as Complete
Mark Scheme
Question 12
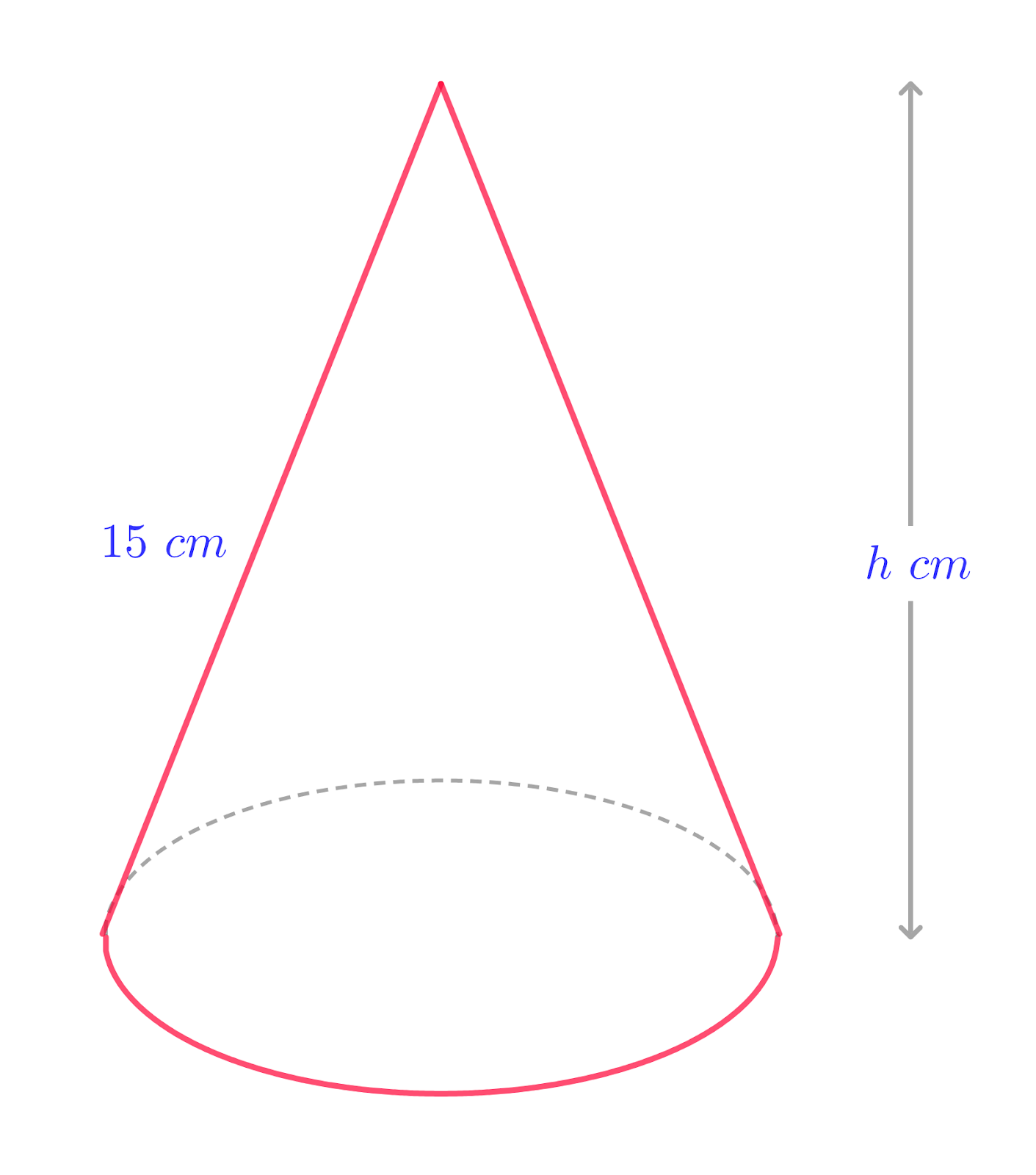
The diagram shows a solid cone which has a slant height of `15` cm and a vertical height `h` cm.
a. Show that the volume `V` cm3, of the cone is given by `v=1/3 pi(225h-h^3)`.
[The volume of a cone of radius `r` and vertical height `h` is `1/3 pi r^2h`]
b. Given that `h` can vary, find the value of `h` for which `V` has a stationary value. Determine, showing all necessary working, the nature of this stationary value.
Hard
Mark as Complete
Mark Scheme
Question 13
A curve is such that `frac{dy}{dx}=x^3-frac{4}{x^2}`. The point `P (2, 9)` lies on the curve. A point moves on the curve in such a way that the x-coordinate is decreasing at a constant rate of `0.05` units per second. Find the rate of change of the y-coordinate when the point is at P.
Easy
Mark as Complete
Mark Scheme
Question 14
A curve has equation `y=(2x-1)^-1 +2x` .
a. Find `frac{dy}{dx}` and `frac{d^2y}{dx^2}`
b. Find the x-coordinates of the stationary points and, showing all necessary working, determine the nature of each stationary point.
Medium
Mark as Complete
Mark Scheme
Question 15
The equation of a curve is `y=2x+1+frac{1}{2x+1}` for `x > -1/2` .
a. Find `(dy)/(dx)` and `(d^2y)/(dx^2)`
b. Find the coordinates of the stationary point and determine the nature of the stationary point.
Medium
Mark as Complete
Mark Scheme
Question 16
Air is being pumped into a balloon in the shape of a sphere so that its volume is increasing at a constant rate of `50` cm3s-1.
Find the rate at which the radius of the balloon is increasing when the radius is `10` cm.
Medium
Mark as Complete
Mark Scheme
Question 17
The equation of a curve is `y=2+sqrt(25-x^2)` .
Find the coordinates of the point on the curve at which the gradient is `4/3` .
Hard
Mark as Complete
Mark Scheme
Question 18
The volume `V` m3 of a large circular mound of iron ore of radius `r` m is modelled by the equation `V=3/2(r-1/2)^3-1` for `rge2` . Iron ore is added to the mound at a constant rate of `1.5` m3 per second.
a. Find the rate at which the radius of the mound is increasing at the instant when the radius is `5.5` m.
b. Find the volume of the mound at the instant when the radius is increasing at `0.1` m per second.
Hard
Mark as Complete
Mark Scheme
Question 19
The equation of a curve is `y=3x+1-4(3x+1)^(1/2` for `x> -1/3`
a. Find `(dy)/(dx)` and `(d^2y)/(dx^2)`
b. Find the coordinates of the stationary point of the curve and determine its nature.
Hard
Mark as Complete
Mark Scheme
Question 20
Water is poured into a tank at a constant rate of `500` cm3 per second. The depth of water in the tank, `t` seconds after filling starts, is `h` cm. When the depth of water in the tank is`h` cm, the volume, `V` cm3, of water in the tank is given by the formula
`V=4/3(25+h)^3-62500/3` .
`a.`Find the rate at which `h` is increasing at the instant when `h=10` cm.
`b.` At another instant, the rate at which `h` is increasing is `0.075` cm per second. Find the value of `V` at this instant.
Hard
Mark as Complete
Mark Scheme
Question 1
Find the gradient of the curve at the point where the curve `y=frac{5x-10}{x^2}` crosses the x-axis.
The curve crosses the x-axis where `y=o`
`y=frac{5x-10}{x^2}` becomes `0=frac{5x-10}{x^2}`
`5x-10=0`
`x=2`
Rewrite `y=frac{5x-10}{x^2}`
`y=frac{5x}{x^2} - frac{10}{x^2}= 5x^-1 - 10x^-2`
`frac{dy}{dx} = -5x^-2 + 20x^-3 =frac{-5}{x^2} + frac{20}{x^3}`
Substitute `x=2` into `frac{dy}{dx}`
`frac{dy}{dx}=frac{-5}{2^2}+frac{20}{2^3}=frac{-5}{4}+frac{20}{8}=frac{5}{4}`
Then the gradient is `frac{5}{4}`
Question 2
Given that `y=2x^3 - 3x^2-36x+5`, find the range of values of `x` for which `frac{dy}{dx} < 0` .
Differentiate`y=`-2`2x^3-3x^2-36x+5`
`frac{dy}{dx}= 6x^2-6x-36`
`6x^2-6x-36 <0`(as `frac{dy}{dx}<0`)
`x^2-x-6<0`
`(x-3)(x+2)<0`
The graph of `y=(x-3)(x+2)` is a `uu` shaped parabola
The x-intercepts are at `x=3` and `x=-2`
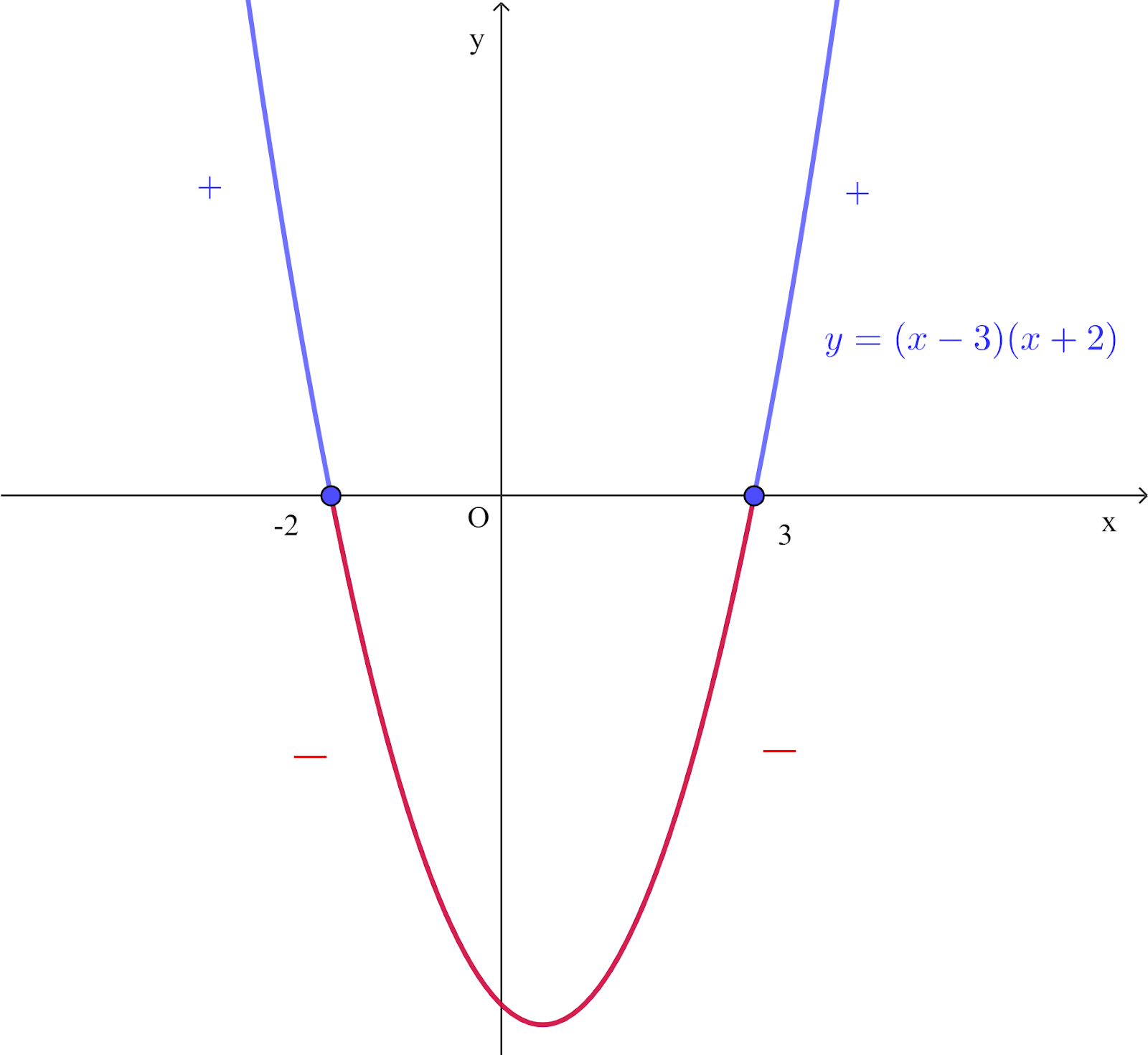
The range of values of `x` for which the curve is negative (below the x-axis)
Then `-2ltxlt3`
Question 3
Differentiate with respect to `x`:
`a. frac{7}{(2x^2-5x)^7}`
`b. frac{6}{root(3)(2-3x)}`
`a.`Let `y= frac{7}{(2x^2 - 5x)^7`
Rewrite as `y= 7(2x^2 - 5x)^-7`
Let `u=2x^2-5x` , then`y=7u^-7`
`frac{du}{dx}=4x-5`
`frac{dy}{du}=-49u^-8`
Use the chain rule to differentiate
`frac{dy}{dx}=frac{dy}{du} xx frac{du}{dx}`
`=-49u^-8 xx(4x-5)`
`=-frac{49(4x-5)}{u^8}`
`=-frac{49(4x-5)}{(2x^2-5x)^8`
`=-frac{49(4x-5)}{[x(2x-5)]^8`
`=-frac{49(4x-5)}{x^8(2x-5)^8`
`b.`Let `y=frac{6}{root(3)(2-3x)}`
Rewrite as`y= 6(2-3x)^(-1/3)`
Let `u=2-3x` , then`y=6u^(-1/3)`
`frac{du}{dx}=-3`
`frac{dy}{du}=-1/3 xx6u^(-4/3) = -2u^(-4/3)`
Use the chain rule to differentiate
`frac{dy}{dx}=frac{dy}{du}xxfrac{du}{dx}`
`=-2u^(-4/3) xx(-3)`
`=6/u^(4/3)`
`=frac{6}{(2-3x)^(4/3)`
`=frac{6}{root(3)((2-3x)^4)}`
Question 4
Find the coordinates of the point on the curve `y=sqrt ((x^2-10x+26))` where the gradient is `0`.
Rewrite `y= sqrt((x^2-10x+26))` as `y=(x^2-10x+26)^(1/2)`
Let `u=x^2-10x+26` , then `y=u^(1/2)`
`frac{du}{dx}=2x-10`
`frac{dy}{du}=1/2 u^(-1/2)`
Use the chain rule to differentiate
`frac{dy}{dx}=frac{dy}{du}xxfrac{du}{dx}`
`=1/2u^(-1/2)xx(2x-10)`
`=frac{1}{2(x^2-10x+26)^(-1/2)} xx(2x-10)`
`=frac{x-5}{sqrt(x^2-10x+26}`
The gradient is zero when `frac{x-5}{sqrt(x^2-10x+26)}=0`
`x-5=0`
`x=5`
Substitute `x=5` into `y=sqrt((x^2-10x+26))`
`y=sqrt((5^2-10(5)+26))=1`
The coordinates of the point are `(5,1)`
Question 5
The normal to the curve `y=x^3 -5x+3` at the point `(-1,7)` intersects the y-axis at the point P. Find the coordinates of P.
Differentiate `y=x^3-5x+3`
`frac{dy}{dx}=3x^2 -5`
The gradient of the curve at `x=-1`
`3(-1)^2-5=-2`
Question 6
The normal to the curve `y = x^3 - 5x + 3` at the point `(-1, 7)` intersects the y-axis at the point P.
Find the coordinates of `P`.
The gradient of the normal `=1/2` (as `m_1xxm_2=-1`)
Equation of the normal
`y-y_1=m(x-x_1)`
`y-7=1/2[x-(-1)]` (as `m=1/2`, `x_1=-1`, `y_1=7`)
`y-7=1/2x+1/2`
`2y-14=x+1`
`2y=x+15`
`2y=0+15` (`x=0` as the normal intersects y-axis at P)
`y=7.5`
Then P has coordinates `(0, 7.5)`
Question 7
The curve `y= 2x^2 +kx -3` at the point `(3,-6)` is parallel to the line `x+5y=10` .
a. Find the value of `k`.
b. Find the coordinates of the point where the normal meets the curve again.
a.Differentiate `y=2x^2 +kx -3`
`frac{dy}{dx}=4x+k`
The gradient of the curve at `x=3`
`4(3) +k =12+k`
The gradient of the normal `=-frac{1}{12+k}` (as `m_1xxm_2=-1` )
The gradient of the line `x+5y=10` is found by rearranging this equation and comparing it with
`y=mx+c`
`5y=-x+10`
`y=-1/5x +2`
The gradient `m=-1/5`
Then `-1/5 =-frac{1}{12+k}`
`12+k=5`
`k=-7`
b.Substitute `k=-7` into `m=- frac{1}{12+k}`
`-frac{1}{12+(-7)}=-1/5`
The equation of the normal
`y-y_1=m(x-x_1)`
`y-(-6)=-1/5(x-3)`(as `m=-1/5` , `x_1=3` , `y_1=-6`)
`y+6=-1/5x+3/5`
`y=-1/5x-27/5` (1)
Substitute `k=-7` into `y=2x^2+kx-3`
`y=2x^2-7x-3` (2)
From (1) and (2)
`2x^2-7x-3=-1/5x-27/5`
`10x^2-35x-15=-x-27`
`10x^2-34x+12=0`
Using quadratic formula `x=frac{-b+-sqrt(b^2-4ac)}{2a}`
`x=frac{-(-34)+-sqrt((-34)^2-4(10)(12))}{2(10)`
`x=frac{34+-sqrt(676)}{20}`
`x=0.4` or `x=3`
Then `x=0.4`
Substitute `x=0.4` into (1)
`y=-1/5(0.4)-27/5=-5.48`
The point where the normal meets the curve again has coordinates `(0.4, −5.48)`
Question 8
Given that `f(x)= frac{2}{sqrt(1-2x)}` , find the value of `f''(-4)`
Rewrite `f(x) frac{2}{sqrt(1-2x)}` as `f(x)=2(1-2x)^(-1/2)`
Use the chain rule to differentiate twice
`f'(x)=-1(1-2x)^(-3/2) xx(-2)=2(1-2x)^(-3/2)`
`f''(x)=-3(1-2x)^(-5/2)xx(-2)=6(1-2x)^(-5/2)`
`f''(-4)=6[1-2(-4)]^(-5/2)=6xx9^(-5/2)=6/sqrt(9)^5=2/81`
Question 9
Given that `y=x^2-2x+5` , show that `4frac{d^2y}{dx^2}+(x-1)frac{dy}{dx}=2y`
Differentiate `y=x^2-2x+5`
`frac{dy}{dx}=2x-2`
`frac{d^2y}{dx^2}=2`
Substitute into `4frac{d^2y}{dx^2}+(x-1)frac{dy}{dx}`
`4xx2+(x-1)(2x-2)`
`=8+2x^2-2x-2x+2`
`=2x^2-4x+10`
As`2y=2(x^2-2x+5)=2x^2-4x+10`
Then `4frac{d^2y}{dx^2}+(x-1)frac{dy}{dx} =2y`
Question 10
A curve has equation `y=x^3+2x^2-4x+6` .
a. Show that `frac{dy}{dx}=0` when `x=-2` and when `x=2/3` .
b. Find the value of `frac{d^2y}{dx^2}` when `x=-2` and when `x=2/3` .
Differentiate `y=x^3 +2x^2-4x+6`
`frac{dy}{dx}=3x^2+4x-4`(1)
`frac{d^2y}{dx^2}=6x+4`(2)
a. Substitute `x=-2` into (1)
`frac{dy}{dx}=3(-2)^2+4(-2)-4`
`frac{dy}{dx}=0`
Substitute `x=2/3` into (1)
`frac{dy}{dx}=3(2/3)^2+4(2/3)-4`
`frac{dy}{dx}=0`
b. Substitute `x=-2` into (2)
`frac{d^2y}{dx^2}=6xx(-2)+4`
`frac{d^2y}{dx^2}=-8`
Substitute `x=2/3` into (2)
`frac{d^2y}{dx^2}=6xx2/3+4`
`frac{d^2y}{dx^2}=8`
Question 11
A curve has equation `y=frac{ax+b}{x^2}` . Given that `frac{ dy}{dx}=0` and `frac{d^2y}{dx^2}=1/2` when `x=2` , find the value of a and the value of `b`.
Rewrite `y=frac{ax+b}{x^2}` as `y=frac{ax}{x^2}+frac{b}{x^2}=ax^-1+bx^-2`
Differentiate `y=ax^-1+bx^-2`
`frac{dy}{dx}=-ax^-2-2bx^-3` (1)
`frac{d^2y}{dx^2}=2ax^-3+6bx^-4` (2)
Substitute `x=2` into (1)
`frac{dy}{dx}=-a(2)^-2-2b(2)^-3`
`frac{dy}{dx}=-frac{a}{4}-frac{2b}{8}`
`frac{dy}{dx}=frac{-a-b}{4}`
`0=frac{-a-b}{a}` (as `frac{dy}{dx}=0`)
`-a-b=0`
`b=-a` (3)
Substitute `x=2` into (2)
`frac{d^2y}{dx^2}=2a(2)^-3+6b(2)^-4`
`frac{d^2y}{dx^2}=(2a)/8 +(6b)/16`
`frac{d^2y}{dx^2}=frac{2a+3b}{8}`
`1/2=frac{2a+3b}{8}` (as `frac{d^2y}{dx^2}=1/2` )
`8=2(2a+3b)`
`2a+3b=4`(4)
From (3) and (4)
`2a+3(-a)=4`
`a=-4`
Substitute `a=-4` into (3)
`b=-(-4)=4`
Question 12

The diagram shows a solid cone which has a slant height of `15` cm and a vertical height `h` cm.
a. Show that the volume `V` cm3, of the cone is given by `v=1/3 pi(225h-h^3)`.
[The volume of a cone of radius `r` and vertical height `h` is `1/3 pi r^2h`]
b. Given that `h` can vary, find the value of `h` for which `V` has a stationary value. Determine, showing all necessary working, the nature of this stationary value.
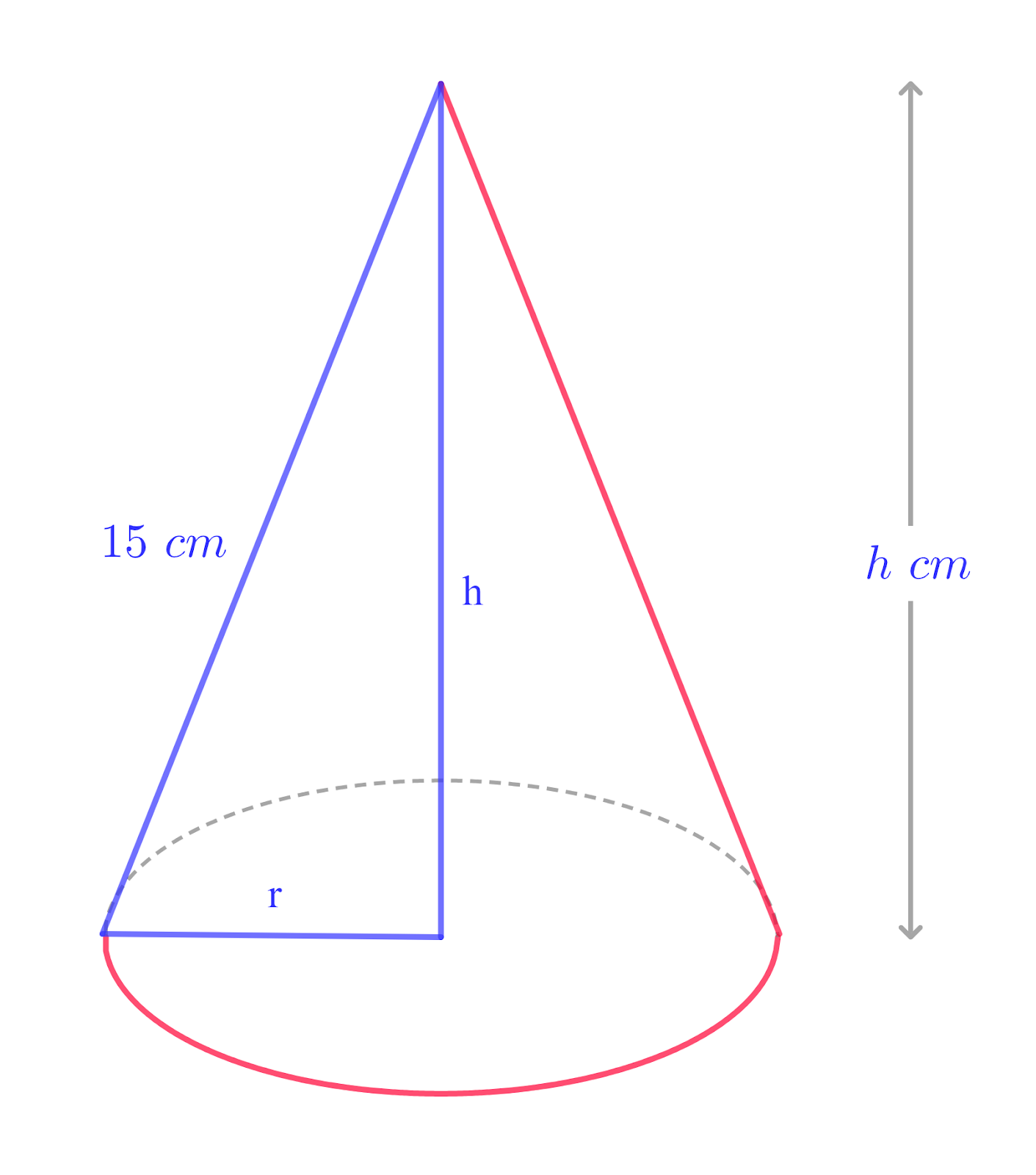
a. Let `r` is the radius of the cone
Use Pythagoras
`r^2+h^2=15^2`
`r^2=225-h^2`
For `V=1/3pir^2h`
`v=1/3pi(225-h^2)h`
`v=1/3pi(225h-h^3)`
b. Differentiate `V=1/3pi(225h-h^3)`
`frac{dv}{dh}=1/3pi(225-3h^2)`
`frac{d^2v}{dh^2}=1/3pi(0-6h)=-2pih` (1)
For `V` has a stationary value
`1/3pi(225-3h^2)=0` (as `frac{dv}{dh}=0`)
`1/3pi(225-3h^2)=0`
`225-3h^2=0`
`3h^2=225`
`h^2=75`
`h=5sqrt3`
Substitute `h=5sqrt3` into (1)
`frac{d^2v}{dh^2}=-2pi(5sqrt3)=-10pisqrt3`
`frac{d^2v}{dh^2}<0`
Then `V` is a maximum value
Question 13
A curve is such that `frac{dy}{dx}=x^3-frac{4}{x^2}`. The point `P (2, 9)` lies on the curve. A point moves on the curve in such a way that the x-coordinate is decreasing at a constant rate of `0.05` units per second. Find the rate of change of the y-coordinate when the point is at P.
Let `frac{dx}{dt}=-0.05`
`frac{dy}{dx}=x^3-frac{4}{x^2}` at the point `P (2, 9)`
`(2)^3-frac{4}{(2)^2}=8-1=7`
Use the chain rule
`frac{dy}{dt}=frac{dy}{dx}xxfrac{dx}{dt}`
`frac{dy}{dt}=7xx(-0.05)`
`frac{dy}{dt}=-0.35`
Then the y-coordinate is decreasing at a rate of `0.35` units per second
Question 14
A curve has equation `y=(2x-1)^-1 +2x` .
a. Find `frac{dy}{dx}` and `frac{d^2y}{dx^2}`
b. Find the x-coordinates of the stationary points and, showing all necessary working, determine the nature of each stationary point.
`a.`Differentiate `y=(2x-1)^-1+2x`
`frac{dy}{dx}=-2(2x-1)^-2+2`
`frac{d^2y}{dx^2}=8(2x-1)^-3` (1)
`b.`For the curve has a stationary value
`-2(2x-1)^-2+2=0` (as `frac{dy}{dx}=0`)
`-2(2x-1)^-2=-2`
`frac{1}{(2x-1)^2}=1`
`2x-1=1`or`2x-1=-1`
`x=1` or `x=0`
Substitute `x=1` into (1)
`8[2(1)-1]^-3=8`
`frac{d^2y}{dx^2}>0` then `x=1` is a minimum value
Substitute `x=0` into (1)
`8[2(0)-1]^-3=-8`
`frac{d^2y}{dx^2}<0` then `x=0` is a maximum value
Question 15
The equation of a curve is `y=2x+1+frac{1}{2x+1}` for `x > -1/2` .
a. Find `(dy)/(dx)` and `(d^2y)/(dx^2)`
b. Find the coordinates of the stationary point and determine the nature of the stationary point.
a. Rewrite `y=2x+1+frac{1}{2x+1}` as `y=2x+1+(2x+1)^-1`
Differentiate `y=2x+1+(2x+1)^-1`
`(dy)/(dx)=2-2(2x+1)^-2=2-frac{2}{(2x+1)^2`
`frac{d^2y}{dx^2}=-2(-4)(2x+1)^-3=frac{8}{(2x+1)^3`
b. For the curve has a stationary value
`2-frac{2}{(2x+1)^2}=0`(as `(dy)/(dx)=0` )
`frac{2}{(2x+1)^2}=2`
`frac{1}{(2x+1)^2}=1`
`2x+1=1`or`2x+1=-1`
`x=0` or `x=-1`
Then `x=0` (as `x> -1/2`)
Substitute `x=0` into `y=2x+1+frac{1}{2x+1}`
`y=2(0)+1+frac{1}{2(0)+1}=2`
The stationary point has coordinates `(0, 2)`
At `(0, 2)`
`frac{d^2y}{dx^2}=frac{8}{[2(0)+1]^3}=8`
`frac{d^2y}{dx^2}>0` then `(0, 2)` is a minimum point
Question 16
Air is being pumped into a balloon in the shape of a sphere so that its volume is increasing at a constant rate of `50` cm3s-1.
Find the rate at which the radius of the balloon is increasing when the radius is `10` cm.
The volume `V=4/3pir^3`
Differentiate `V=4/3pir^3`
`frac{dv}{dr}=4/3pi(3r^2)=4pir^2`
Let `r=10`
`frac{dv}{dr}=4pi(10)^2=400pi`
`frac{dr}{dv}=frac{1}{(dv)/(dr)}=frac{1}{400pi}`
Let `frac{dv}{dt}=50`
Use the chain rule
`frac{d}{dt}=frac{dr}{dv}xxfrac{dv}{dt}`
`frac{dr}{dt}=frac{1}{400pi}xx50`
`frac{dr}{dt}=frac{1}{8pi}`
Then the rate is `frac{1}{8pi}` cm/s
Question 17
The equation of a curve is `y=2+sqrt(25-x^2)` .
Find the coordinates of the point on the curve at which the gradient is `4/3` .
Rewrite `y=2+sqrt(25-x^2)`as `y=2+(25-x^2)^(1/2)`
Differentiate `y=2+(25-x^2)^(1/2)`
`frac{dy}{dx}=1/2(-2x)(25-x^2)^(-1/2)=-frac{x}{sqrt(25-x^2)`
`4/3=-frac{x}{sqrt(25-x^2)` (as `frac{dy}{dx}=4/3`)
`16/9=frac{x^2}{25-x^2}`
`16(25-x^2)=9x^2`
`400-16x^2=9x2`
`400=25x^2`
`x^2=16`
`x=4` or `x=-4`
Substitute `x=4` into `(dy)/(dx)=-frac{x}{sqrt(25-x^2)`
`-frac{4}{sqrt(25-(4)^2)}=-4/3ne4/3`
Then `x=-4`
Substitute `x=-4` into `y=2+sqrt(25-x^2)`
`2+sqrt(25-(-4)^2)=5`
The point has coordinates `(-4, 5)`
Question 18
The volume `V` m3 of a large circular mound of iron ore of radius `r` m is modelled by the equation `V=3/2(r-1/2)^3-1` for `rge2` . Iron ore is added to the mound at a constant rate of `1.5` m3 per second.
a. Find the rate at which the radius of the mound is increasing at the instant when the radius is `5.5` m.
b. Find the volume of the mound at the instant when the radius is increasing at `0.1` m per second.
a. Differentiate `V=3/2(-1/2)^3-1`
`(dv)/(dr)=3/2(3)(r-1/2)^2=9/2(r-1/2)^2` (1)
Let `r=5.5`
`(dv)/(dr)=9/2(5.5-1/2)^2=112.5`
`(dr)/(dr)=frac{1}{(dv)/(dr)}=1/112.5`
Let `(dv)/(dt)=1.5`
Use the chain rule
`(dr)/(dt)=(dr)/(dv)xx(dv)/(dt)`
`(dr)/(dt)=1/112.5xx1.5`
`(dr)/(dt)=1/75`
Then the rate is `1/75` m/s
b. Let`(dr)/(dt)=1`
`(dt)/(dr)=frac{1}{(dr)/(dt)}=1/0.1`
Use the chain rule
`(dv)/(dr)=(dv)/(dt)xx(dt)/(dr)`
`(dv)/(dr)=1.5xx1/0.1`
`(dv)/(dr)=15`
From (1)
`15=9/2(r-1/2)^2`
`(r-1/2)^2=10/3`
`r-1/2=sqrt(10/3)`or`r-1/2=-sqrt(10/3)`
`r=1/2+sqrt(10/3)`or `r=1/2-sqrt(10/3) <0`
Then `r=1/2+sqrt(10/3)`
Substitute `r=1/2+sqrt(10/3)` into `V=3/2(r-1/2)^3-1`
`V=3/2(1/2+sqrt(10/3)-1/2)^3-1=8.13`
Then the volume is `8.13` m3
Question 19
The equation of a curve is `y=3x+1-4(3x+1)^(1/2` for `x> -1/3`
a. Find `(dy)/(dx)` and `(d^2y)/(dx^2)`
b. Find the coordinates of the stationary point of the curve and determine its nature.
a. Differentiate `y=3x+1-4(3x+1)^(1/2)`
`(dy)/(dx)=3-4(1/2)(3)(3x+1)^(-1/2)=3-6(3x+1)^(-1/2)`
`(d^2y)/(dx^2)=-6(-1/2)(3)(3x+1)^(-3/2)=9(3x+1)^(-3/2)`
b. For the curve has a stationary value
`3-6(3x+1)^(-1/2)=0`(as `(dy)/(dx)=0` )
`3-frac{6}{sqrt(3x+1)}=0`
`sqrt(3x+1)=2`
`3x+1=4`
`x=1`
Substitute `x=1` into `y=3x+1-4(3x+1)^(1/2)`
`3(1)+1-4[3(1)+1]^(1/2)=-4`
The stationary point has coordinates `(1, −4)`
At `(1, −4)`
`frac{d^2y}{dx^2}=9[3(1)+1]^(-3/2)=9/8`
`frac{d^2y}{dx^2}>0`then `(1, −4)` is a minimum point
Question 20
Water is poured into a tank at a constant rate of `500` cm3 per second. The depth of water in the tank, `t` seconds after filling starts, is `h` cm. When the depth of water in the tank is`h` cm, the volume, `V` cm3, of water in the tank is given by the formula
`V=4/3(25+h)^3-62500/3` .
`a.`Find the rate at which `h` is increasing at the instant when `h=10` cm.
`b.` At another instant, the rate at which `h` is increasing is `0.075` cm per second. Find the value of `V` at this instant.
a. Differentiate `V=4/3(25+h)^3-62500/3`
`(dv)/(dh)=4/3(3)(25+h)^2=4(25+h)^2` (1)
Let `h=10`
`(dv)/(dh)=4(25+10)^2=4900`
`(dh)/(dv)=1/{(dv)/(dh)}=1/4900`
Let `(dv)/(dt)=500`
Use the chain rule
`(dh)/(dt)=(dh)/(dv)xx(dv)/(dt)`
`(dh)/(dt)=1/4900xx500`
`(dh)/(dt)=0.102`
Then the rate is `0.102` cm/s
b. Let `(dh)/(dt)=0.075`
`(dt)/(dh)=1/((dh)/(dt))=1/0.075`
Use the chain rule
`(dv)/(dh)=(dv)/(dt)xx(dt)/(dh)`
`4(25+h)^2=500xx1/0.075`
`4(25+h)^2=20000/12`
`(25+h)^2=5000/3`
`25+h=sqrt(5000/3)` or `25+h=-sqrt(5000/3)`
`h=15.825` or `h=-65.825<0`
Then `h=15.825`
Substitute `h=15.825` into `V=4/3(25+h)^3-62500/3`
`4/3(25+15.825)^3-62500/3=69889~~69900`
Then the volume is `69900` cm3
Question 1
Find the gradient of the curve at the point where the curve `y=frac{5x-10}{x^2}` crosses the x-axis.
Question 2
Given that `y=2x^3 - 3x^2-36x+5`, find the range of values of `x` for which `frac{dy}{dx} < 0` .
Question 3
Differentiate with respect to `x`:
`a. frac{7}{(2x^2-5x)^7}`
`b. frac{6}{root(3)(2-3x)}`
Question 4
Find the coordinates of the point on the curve `y=sqrt ((x^2-10x+26))` where the gradient is `0`.
Question 5
The normal to the curve `y=x^3 -5x+3` at the point `(-1,7)` intersects the y-axis at the point P. Find the coordinates of P.
Question 6
The normal to the curve `y = x^3 - 5x + 3` at the point `(-1, 7)` intersects the y-axis at the point P.
Find the coordinates of `P`.
Question 7
The curve `y= 2x^2 +kx -3` at the point `(3,-6)` is parallel to the line `x+5y=10` .
a. Find the value of `k`.
b. Find the coordinates of the point where the normal meets the curve again.
Question 8
Given that `f(x)= frac{2}{sqrt(1-2x)}` , find the value of `f''(-4)`
Question 9
Given that `y=x^2-2x+5` , show that `4frac{d^2y}{dx^2}+(x-1)frac{dy}{dx}=2y`
Question 10
A curve has equation `y=x^3+2x^2-4x+6` .
a. Show that `frac{dy}{dx}=0` when `x=-2` and when `x=2/3` .
b. Find the value of `frac{d^2y}{dx^2}` when `x=-2` and when `x=2/3` .
Question 11
A curve has equation `y=frac{ax+b}{x^2}` . Given that `frac{ dy}{dx}=0` and `frac{d^2y}{dx^2}=1/2` when `x=2` , find the value of a and the value of `b`.
Question 12

The diagram shows a solid cone which has a slant height of `15` cm and a vertical height `h` cm.
a. Show that the volume `V` cm3, of the cone is given by `v=1/3 pi(225h-h^3)`.
[The volume of a cone of radius `r` and vertical height `h` is `1/3 pi r^2h`]
b. Given that `h` can vary, find the value of `h` for which `V` has a stationary value. Determine, showing all necessary working, the nature of this stationary value.
Question 13
A curve is such that `frac{dy}{dx}=x^3-frac{4}{x^2}`. The point `P (2, 9)` lies on the curve. A point moves on the curve in such a way that the x-coordinate is decreasing at a constant rate of `0.05` units per second. Find the rate of change of the y-coordinate when the point is at P.
Question 14
A curve has equation `y=(2x-1)^-1 +2x` .
a. Find `frac{dy}{dx}` and `frac{d^2y}{dx^2}`
b. Find the x-coordinates of the stationary points and, showing all necessary working, determine the nature of each stationary point.
Question 15
The equation of a curve is `y=2x+1+frac{1}{2x+1}` for `x > -1/2` .
a. Find `(dy)/(dx)` and `(d^2y)/(dx^2)`
b. Find the coordinates of the stationary point and determine the nature of the stationary point.
Question 16
Air is being pumped into a balloon in the shape of a sphere so that its volume is increasing at a constant rate of `50` cm3s-1.
Find the rate at which the radius of the balloon is increasing when the radius is `10` cm.
Question 17
The equation of a curve is `y=2+sqrt(25-x^2)` .
Find the coordinates of the point on the curve at which the gradient is `4/3` .
Question 18
The volume `V` m3 of a large circular mound of iron ore of radius `r` m is modelled by the equation `V=3/2(r-1/2)^3-1` for `rge2` . Iron ore is added to the mound at a constant rate of `1.5` m3 per second.
a. Find the rate at which the radius of the mound is increasing at the instant when the radius is `5.5` m.
b. Find the volume of the mound at the instant when the radius is increasing at `0.1` m per second.
Question 19
The equation of a curve is `y=3x+1-4(3x+1)^(1/2` for `x> -1/3`
a. Find `(dy)/(dx)` and `(d^2y)/(dx^2)`
b. Find the coordinates of the stationary point of the curve and determine its nature.
Question 20
Water is poured into a tank at a constant rate of `500` cm3 per second. The depth of water in the tank, `t` seconds after filling starts, is `h` cm. When the depth of water in the tank is`h` cm, the volume, `V` cm3, of water in the tank is given by the formula
`V=4/3(25+h)^3-62500/3` .
`a.`Find the rate at which `h` is increasing at the instant when `h=10` cm.
`b.` At another instant, the rate at which `h` is increasing is `0.075` cm per second. Find the value of `V` at this instant.