Question 1
A curve with equation `y = f(x)` is such that `f′(x)` `=2x^(-1/3)-x^(1/3)`. It is given that `f (8) = 5`. Find `f(x)`
Easy
Mark as Complete
Mark Scheme
Question 2
A curve is such that `(dy)/(dx)=frac{6}{(3x-2)^3` and `A (1, −3)` lies on the curve. A point is moving along the curve and at A the y-coordinate of the point is increasing at `3` units per second.
a. Find the rate of increase at A of the x-coordinate of the point.
b. Find the equation of the curve.
Medium
Mark as Complete
Mark Scheme
Question 3
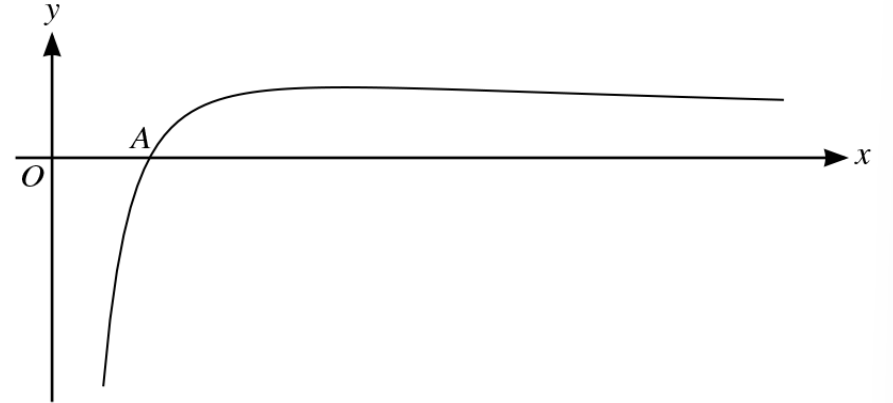
The diagram shows the curve with equation `y = 9 ( x^(-1/2 )− 4x^(-3/2))`. The curve crosses the x-axis at the point A.
a. Find the x-coordinate of A.
b. Find the equation of the tangent to the curve at A.
c. Find the x-coordinate of the maximum point of the curve.
d. Find the area of the region bounded by the curve, the x-axis and the line `x=9`.
Medium
Mark as Complete
Mark Scheme
Question 4
The equation of a curve is `y = 2sqrt( 3x +4) − x`.
a. Find the equation of the normal to the curve at the point `(4, 4)`, giving your answer in the form `y = mx + c`
b. Find the coordinates of the stationary point
c. Determine the nature of the stationary point
d. Find the exact area of the region bounded by the curve, the x-axis and the lines `x = 0` and `x = 4`
Medium
Mark as Complete
Mark Scheme
Question 5
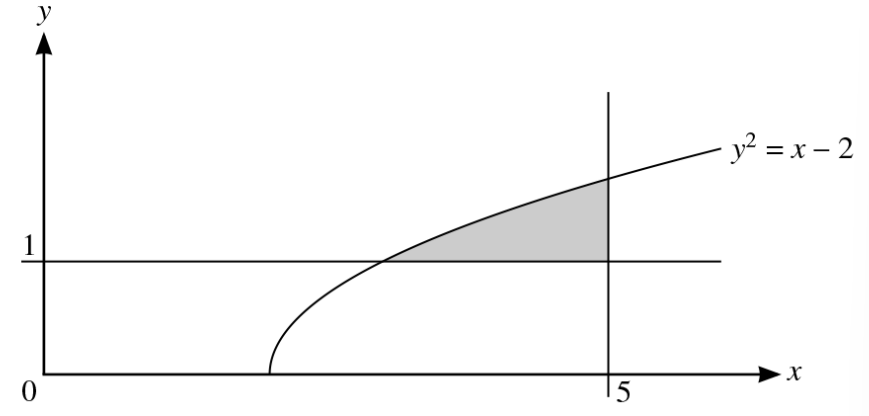
The diagram shows part of the curve with equation `y^2 = x − 2` and the lines `x = 5` and `y = 1`. The shaded region enclosed by the curve and the lines is rotated through `360°` about the x-axis. Find the volume obtained.
Medium
Mark as Complete
Mark Scheme
Question 6
The gradient of a curve is given by `(dy)/dx = 6(3x – 5)^3 − kx^2` , where `k` is a constant. The curve has a stationary point at `(2, −3.5)`.
a. Find the value of `k`
b. Find the equation of the curve
c. Find `(d^2y)/dx^2`
d. Determine the nature of the stationary point `(2, -3.5)`
Medium
Mark as Complete
Mark Scheme
Question 7
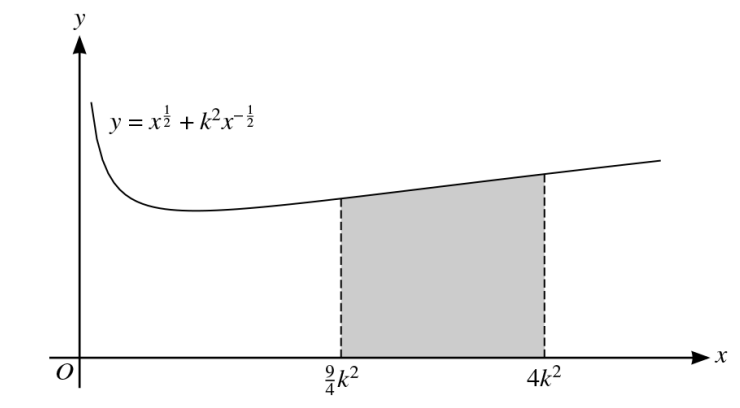
The diagram shows part of the curve with equation `y = x^(1/2) + k^(2x^(-1/2))`, where `k` is a positive constant.
a. Find the coordinates of the minimum point of the curve, giving your answer in terms of `k`.
The tangent at the point on the curve where `x = 4k^2` intersects the y-axis at P.
b. Find the y-coordinate of P in terms of `k`.
The shaded region is bounded by the curve, the x-axis and the lines `x = 9/4k^2` and `x = 4k^2`.
c. Find the area of the shaded region in terms of `k`.
Medium
Mark as Complete
Mark Scheme
Question 8
A curve has equation `y = f'(x)`, and it is given that `f'(x) = 2x^2 – 7 – 4/(x^2)`.
a. Given that `f(1) = –1/3` , find `f(x)`.
b. Find the coordinates of the stationary points on the curve.
c. Find `f''(x)`
d. Hence, or otherwise, determine the nature of each of the stationary points.
Medium
Mark as Complete
Mark Scheme
Question 9
a. Find `int_1^oofrac{1}{(3x-2)^(3/2)}dx`
b.
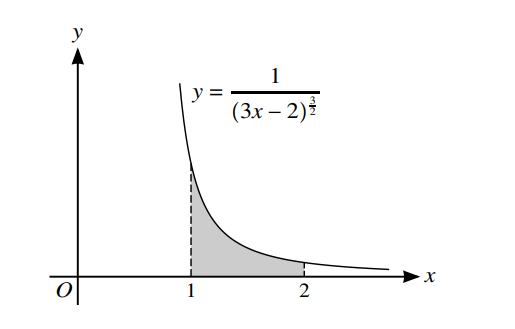
The diagram shows the curve with equation `y = 1/(3x-2)^(3/2)`. The shaded region is bounded by the curve, the x-axis and the lines `x = 1` and `x = 2`. The shaded region is rotated through `360^o` about the x-axis.
Find the volume of revolution.
The normal to the curve at the point `(1, 1)` crosses the y-axis at the point A.
c. Find the y-coordinate of A.
Medium
Mark as Complete
Mark Scheme
Question 10
A curve is such that `(dy)/dx= 8/((3x + 2)^2`. The curve passes through the point `(2, 5_3^2)`. Find the equation of the curve.
Easy
Mark as Complete
Mark Scheme
Question 11
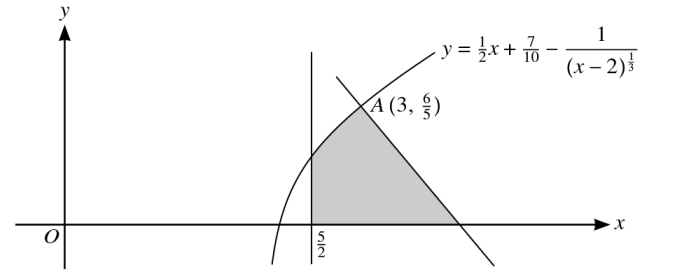
The diagram shows the line `x=5/2`, part of the curve `y = 1/2 x + 7/10 − 1/((x -2)^(1/3))` and the normal to the curve at the point A `(3, 6/5)`.
a. Find the x-coordinate of the point where the normal to the curve meets the x-axis.
b. Find the area of the shaded region, giving your answer correct to `2` decimal places.
Hard
Mark as Complete
Mark Scheme
Question 12
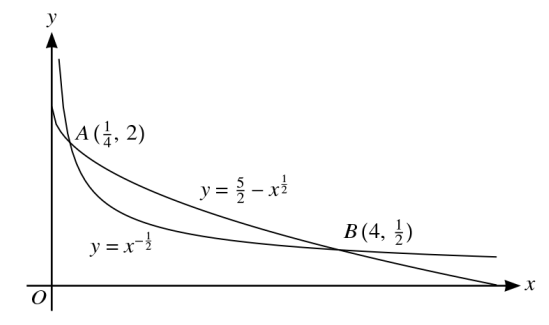
The diagram shows the curves with equations `y = y = x^(-1/2)` and `y = 5/2 - x^(1/2)` . The curves intersect at the points A `(1/4 , 2)` and B `(4, 1/2)`.
a. Find the area of the region between the two curves.
b. The normal to the curve `y = y = x^(-1/2)` at the point `(1, 1)` intersects the y-axis at the point `(0, p)`.
Find the value of `p`.
Hard
Mark as Complete
Mark Scheme
Question 13
A curve has equation`y = f(x)` and it is given that `f'(x) = (1/2x + k)^-2 – (1 + k)^-2`, where `k` is a constant. The curve has a minimum point at `x =2`.
a. Find `f′′(x)` in terms of `k` and `x`, and hence find the set of possible values.
b. It is now given that `k = −3` and the minimum point is at `(2, 3 1/2)`. Find `f(x)`.
c. Find the coordinates of the other stationary point and determine its nature.
Medium
Mark as Complete
Mark Scheme
Question 14
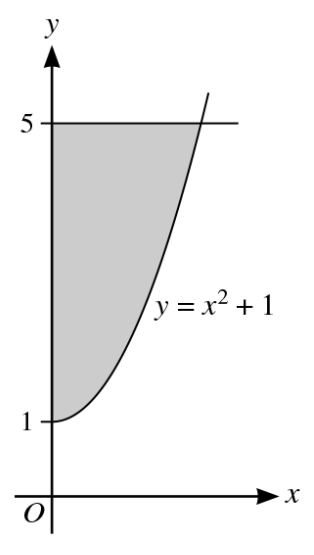
The diagram shows part of the curve with equation`y = x^2 + 1`. The shaded region enclosed by the curve, the y-axis and the line `y = 5` is rotated through `360^0` about the y-axis. Find the volume obtained.
Easy
Mark as Complete
Mark Scheme
Question 15
A curve has equation `y = x^2 − 2x − 3`. A point is moving along the curve in such a way that at P the y-coordinate is increasing at `4` units per second and the x-coordinate is increasing at `6` units per second. Find the x-coordinate of P.
Easy
Mark as Complete
Mark Scheme
Question 16
The gradient of a curve at the point `(x, y)` is given by `(dy)/dx = 2(x + 3)^(1/2) − x`. The curve has a stationary point at `(a, 14)`, where `a` is a positive constant.
a. Find the value a.
b. Determine the nature of the stationary point.
c. Find the equation of the curve.
Medium
Mark as Complete
Mark Scheme
Question 17
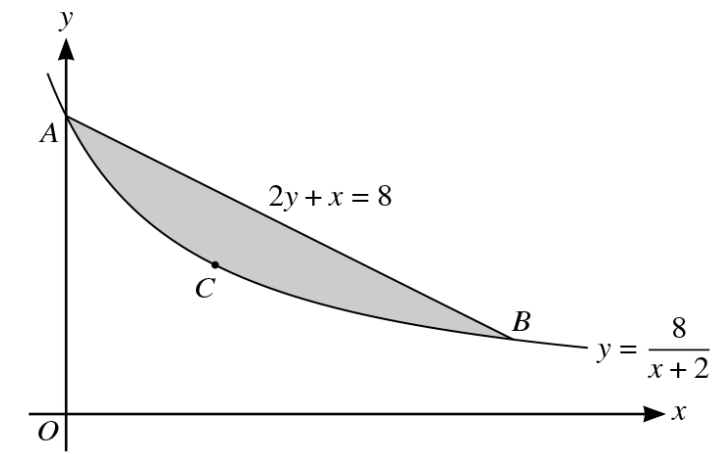
The diagram shows part of the curve `y = 8/(x +2)` and the line `2y + x = 8`, intersecting at points A and B. The point C lies on the curve and the tangent to the curve at C is parallel to AB.
a.Find, by calculation, the coordinates of A, B and C. [6]
b.Find the volume generated when the shaded region, bounded by the curve and the line, is rotated through `360^o`about the x-axis. [6]
Hard
Mark as Complete
Mark Scheme
Question 18
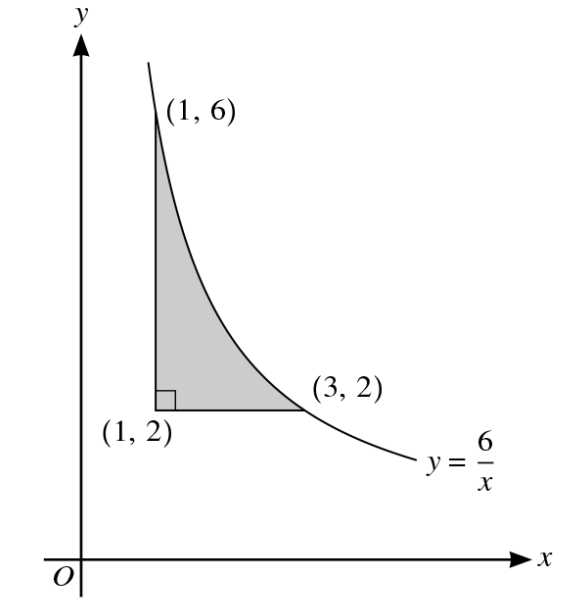
The diagram shows part of the curve `y = 6/x`. The points `(1, 6)` and `(3, 2)` lie on the curve. The shaded region is bounded by the curve and the lines `y = 2` and `x = 1`.
a. Find the volume generated when the shaded region is rotated through `360^o` about the y-axis. [5]
b.The tangent to the curve at a point X is parallel to the line `y + 2x = 0`. Show that X lies on the line `y = 2x`. [3]
Medium
Mark as Complete
Mark Scheme
Question 19
The equation of a curve is such that `(dy)/dx = 3x^(1/2) −3x^(-1/2)`. It is given that the point `(4, 7)` lies on the curve. Find the equation of the curve. [4]
Easy
Mark as Complete
Mark Scheme
Question 20
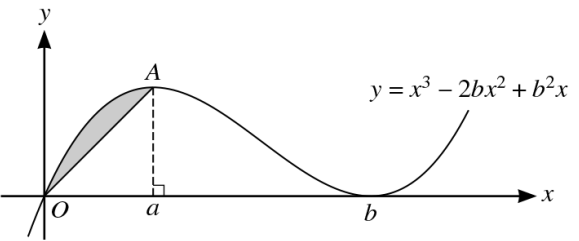
The diagram shows part of the curve with equation `y = x^3 − 2bx^2 + b^2x` and the line OA, where A is the maximum point on the curve. The x-coordinate of A is a and the curve has a minimum point at `(b, 0)`, where a and b are positive constants.
a.Show that `b = 3a`. [4]
b.Show that the area of the shaded region between the line and the curve is `ka^4`, where k is a fraction to be found. [7]
Hard
Mark as Complete
Mark Scheme
Question 1
A curve with equation `y = f(x)` is such that `f′(x)` `=2x^(-1/3)-x^(1/3)`. It is given that `f (8) = 5`. Find `f(x)`
`int(2x^(-1/3) - x^(1/3))dx` (apply the formula `intx^alphadx=frac{1}{alpha+1}x^(alpha+1)+C`)
`=frac{2x^(2/3)}{2/3} -frac{x^(4/3)}{4/3}+C`
`f (8) = 5`
`frac{2x8^(2/3)}{2/3}-frac{8^(4/3)}{4/3}+C=5`
`C = 5`
`f(x)=3x^(2/3)-3/4x^(4/3)+5`
Question 2
A curve is such that `(dy)/(dx)=frac{6}{(3x-2)^3` and `A (1, −3)` lies on the curve. A point is moving along the curve and at A the y-coordinate of the point is increasing at `3` units per second.
a. Find the rate of increase at A of the x-coordinate of the point.
b. Find the equation of the curve.
a At `x =1`, `(dy)/(dx)=6`[1]
`(dx)/(dt)=((dx)/(dy)xx(dy)/(dt))=1/6xx3=1/2`
b. `y = (frac{6(2x-2)^(-2)}{-2})-:(3)[+C]` (Substitute `x = 1`, `y = -3`)
`-3 = -1 + C`
`y = -(3x - 2)^-2 – 2`
Question 3

The diagram shows the curve with equation `y = 9 ( x^(-1/2 )− 4x^(-3/2))`. The curve crosses the x-axis at the point A.
a. Find the x-coordinate of A.
b. Find the equation of the tangent to the curve at A.
c. Find the x-coordinate of the maximum point of the curve.
d. Find the area of the region bounded by the curve, the x-axis and the line `x=9`.
a. x-coordinate of A leads to `y = 0`
`9 x (x^(-1/2) − 4x^(-3/2)) = 0`
`9x^(3/2) ( x – 4) = 0`
Solve out we have `x = 0` and `x = 4` (accept)
b. `(dy)/(dx)=9(-1/2x^(-3/2)+6x^(-5/2))`
At `x = 4` gradient `= 9(-1/16 + 6/32) = 9/8`
Equation is `y = 9/8 (x - 4)`
c. `9x^(-5/2)(-1/2x+6)=0`
`x = 12`
d. `int9(x^(-1/2) - 4x^(-3/2))dx = 9(frac{x^(1/2)}{1/2}-frac{x^(-1/2)}{-1/2})`[2]
`= 9[(6 + 8/3) - (4+4)]`
`= 6`
Question 4
The equation of a curve is `y = 2sqrt( 3x +4) − x`.
a. Find the equation of the normal to the curve at the point `(4, 4)`, giving your answer in the form `y = mx + c`
b. Find the coordinates of the stationary point
c. Determine the nature of the stationary point
d. Find the exact area of the region bounded by the curve, the x-axis and the lines `x = 0` and `x = 4`
a. `(dy)/(dx) = 3(3x +4)^(-0.5) – 1`
Gradient of tangent `= – 1/4` and the gradient of normal `= 4`
Equation of line is `(y – 4) = 4(x – 4)` or evaluate C
So `y = 4x -12`
b. `3(3x +4)^(-0.5) – 1 = 0`
Solving as far as `x = 5/3`
`y = 2(3 xx 5/3 + 4)^0.5 – 5/3 = – 13/5`
c. `(d^2y)/(dx^2)=-9/2(3x+4)^-1.5`
At `x = 5/3` `(d^2y)/(dx^2)` is negative so the point is a maximum
d. `Area=int 2(3x + 4)^0.5 – xdx`
`= 4/9(3x + 4)^1.5 – 1/2 x^2`
`= (4/9 (16)^1.5 – 1/2 (4)^2) – 4/9(4)^1.5`
`= 256/9 – 8 – 32/9`
`= 152/9 = 16_9^8`
Question 5

The diagram shows part of the curve with equation `y^2 = x − 2` and the lines `x = 5` and `y = 1`. The shaded region enclosed by the curve and the lines is rotated through `360°` about the x-axis. Find the volume obtained.
Curve intersects `y = 1` at `(3, 1)`
Volume`= [pi]int(x – 2) d[x]`
`[pi][1/2 x^2 – 2x] or [pi][1/2(x –2)^2]`
`= [pi][(5^2/2 – 2 xx 5) – ((3^2)/2 – 2 xx 3)]`
`= [pi](5/2 + 3/2)`as a minimum requirement for their values
Volume of cylinder `= pi xx 1^2 x ( 5 – 3) = 2 pi`
Volume of solid `= 4 pi – 2pi = 2pi (~6.28)`
Question 6
The gradient of a curve is given by `(dy)/dx = 6(3x – 5)^3 − kx^2` , where `k` is a constant. The curve has a stationary point at `(2, −3.5)`.
a. Find the value of `k`
b. Find the equation of the curve
c. Find `(d^2y)/dx^2`
d. Determine the nature of the stationary point `(2, -3.5)`
a. At stationary point `(dy)/dx = 0` so `6(3 xx 2 – 5)^3 – k xx 2^2 = 0`
`k = 3/2`
b. `y = 6/(4 xx 3) (3x – 5)^4 – 1/3 kx^3 +C`
`-7/2 = 1/2( 3 xx 2 – 5)^4 – 1/3 xx 3/2 xx 2^3 + C` (leading to`–3.5 + C = –3.5`)
`y = 1/2(3x – 5)^4 – 1/2 x^3`
c. `[3 x][18 (3x -5)^2][– 2kx]`
`486x^2 1623x + 1350` or `– 1620x – 2kx`
d. At `x = 2`, `(d^2y)/dx^2 = 54(3 xx 3 – 5)^2 – 4k`
`= 48 > 0`, so it is minimum
Question 7

The diagram shows part of the curve with equation `y = x^(1/2) + k^(2x^(-1/2))`, where `k` is a positive constant.
a. Find the coordinates of the minimum point of the curve, giving your answer in terms of `k`.
The tangent at the point on the curve where `x = 4k^2` intersects the y-axis at P.
b. Find the y-coordinate of P in terms of `k`.
The shaded region is bounded by the curve, the x-axis and the lines `x = 9/4k^2` and `x = 4k^2`.
c. Find the area of the shaded region in terms of `k`.
a. `(dy)/dx = 1/2 x^(-1/2) – 1/2 k^2 x^(-3/2)`
`1/2 x^(-1/2) – 1/2 k^2 x^(-3/2) = 0` leading to `1/2 x^(-1/2) = 1/2 k^2 x^(-3/2)`
`(k^2, 2k)`
b. When `x = 4k^2`, `(dy)/dx = [1/(4k) – 1/(16k) ] = 3/(16k)`
`y = [2k + k^2 xx 1/(2k) ] = (5k)/ 2`
Equation of tangent is `y – (5k)/ 2 = 1/ (16k)(x – 4k^2)`
When `x = 0`, `y = [(5k)/2 – (3k)/4] = (7k)/4`
c. `int(x^(1/2) + k^(2x^(-1/2)))dx = (2x^(3/2))/3 + 2k^(2x^(1/2))`
`= ((16k^3)/3 + 4k^3) – ((9k^3)/4 + 3k^3)`
`= (49k^3)/12`
Question 8
A curve has equation `y = f'(x)`, and it is given that `f'(x) = 2x^2 – 7 – 4/(x^2)`.
a. Given that `f(1) = –1/3` , find `f(x)`.
b. Find the coordinates of the stationary points on the curve.
c. Find `f''(x)`
d. Hence, or otherwise, determine the nature of each of the stationary points.
`a.``f(x) = 2/3 x^3 – 7x + 4x^(-1) [+C]`
`-1/3 = 2/3 – 7 + 4 + c` leading to `C= 2`
`f(x) = 2/3x^3 – 7x + 4x^-1 + 2`
b. `2x^4 – 7x^2 – 4 = 0`
`(2x^2 +1)(x^2 – 4) = 0`
`x = +- 2`
`2/3(2)^3 – 7(2) + 4/2 + 2` leading to we have point A
`(2, –14/3)`
`2/3(-2)^3 – 7(-2) + 4/-2 + 2` leading to we have point `B (- 2, 26/3)`
c. `f''(x) = 4x + 8x^-3`
`f''(2) = 9 > 0`, minimum at `x = 2`
`f''(– 2) = – 9 <0` maximum at `x = -2`
Question 9
a. Find `int_1^oofrac{1}{(3x-2)^(3/2)}dx`
b.

The diagram shows the curve with equation `y = 1/(3x-2)^(3/2)`. The shaded region is bounded by the curve, the x-axis and the lines `x = 1` and `x = 2`. The shaded region is rotated through `360^o` about the x-axis.
Find the volume of revolution.
The normal to the curve at the point `(1, 1)` crosses the y-axis at the point A.
c. Find the y-coordinate of A.
a. `((3x - 2)^(-1/2))/(-1/2) : 3`
`-2/3 [0 -1]`
`2/3`
b. `[π]inty^2dx = [π]int(3x -2)^-3dx = [pi]frac{(3x -2)^-2}{-2 xx 3}`
`[π][-1/6][1/16 -1]`
`(5π)/32`
c. `(dy)/dx = -3/2 xx 3(3x -2)^(-5/2)`
At `x = 1`, `(dy)/dx = -9/2`
`y -1 = 2/9(x-1)`
At A, `y = 7/9`
Question 10
A curve is such that `(dy)/dx= 8/((3x + 2)^2`. The curve passes through the point `(2, 5_3^2)`. Find the equation of the curve.
`int8/((3x + 2)^2)dx`
`y = frac{8/3}{(3x+2)}+C`
`5_3^2 = - frac{8/3}{(3x+2+2)} + C`
`C = 6`
So `y=frac{8/3}{3(3x+2)}+6`
Question 11

The diagram shows the line `x=5/2`, part of the curve `y = 1/2 x + 7/10 − 1/((x -2)^(1/3))` and the normal to the curve at the point A `(3, 6/5)`.
a. Find the x-coordinate of the point where the normal to the curve meets the x-axis.
b. Find the area of the shaded region, giving your answer correct to `2` decimal places.
a. `(dy)/dx = 1/2 + frac{1}{2(x- 2)^(4/3)}`
`(dy)/dx` at `x = 3 [1/2 + frac{1}{3(3 -2)^(4/3) }= 5/6]`
Gradient of normal `= frac{-1}{(dy)/dx} [ = -6/5]`
Equation of normal `y - 65`(their normal gradient) `(x-3)`
`[ y=-6/5x + 4.8 ⟹ 5y = 6x + 24]`
When `y = 0`, `x = 4`
`b.`Area under curve `= int(1/2 x + 7/10 -frac{1}{(x -2)^(1/3)})dx`
`= 1/4 x^2 + 7/10x - frac{3(x-2)^(2/3)}{2}`
`= (9/4 + 2.1 -3/2) -(6.25/4 + 1.75 - frac{3 xx 0.5^(2/3)}{4})`
`= 0.48`
Area of triangle `= 0.6`
Total area `= 0.6 + 0.48 = 1.08`
Question 12

The diagram shows the curves with equations `y = y = x^(-1/2)` and `y = 5/2 - x^(1/2)` . The curves intersect at the points A `(1/4 , 2)` and B `(4, 1/2)`.
a. Find the area of the region between the two curves.
b. The normal to the curve `y = y = x^(-1/2)` at the point `(1, 1)` intersects the y-axis at the point `(0, p)`.
Find the value of `p`.
a. `int(5/2 - x^(-1/2)-x^(-1/2))dx`
`{5/2x- 2/3x^(3/2)}{-}{2x^(1/2)}`
`(10 - 16/3 - 4)-(5/8 -1/12 -1)`
`9/8` or `1.125`
b. `(dy)/dx = -1/2 x^(-3/2)`
When `x =1`, `m=- 1/2`
`y – 1 = 2(x - 1)`
Through `(1,1)` with gradient `-1/m` or `(1 -p)/1 = 2`
When `x = 0`, `p = - 1`
Question 13
A curve has equation`y = f(x)` and it is given that `f'(x) = (1/2x + k)^-2 – (1 + k)^-2`, where `k` is a constant. The curve has a minimum point at `x =2`.
a. Find `f′′(x)` in terms of `k` and `x`, and hence find the set of possible values.
b. It is now given that `k = −3` and the minimum point is at `(2, 3 1/2)`. Find `f(x)`.
c. Find the coordinates of the other stationary point and determine its nature.
a. `f′′(x) = -(1/2x + k)^-3`
`f′′(2) > 0 ⟹ (1 + k)^-3 > 0`
`k < -1`
b. `[ f(x) = int(1/2x - 3)^-2 -(-2)^-2)dx] {((1/2x -3)^-1)/(-1 x 1/2)}{-x/4}`
`3_2^1 = 1 - 1/2 + C`
`f(x) = frac{- 2}{(1/2 x -3)} - x/4 + 3`
c. `(1/2 x -3)^-2 - (-2)^-2 = 0`
leading to `(1/2 x -3)^-2 = 4`, from that `x = 10`
`(10, - 1/2)`
`f′′(10) [ = (5-3)^-3] <0` so Maximum
Question 14

The diagram shows part of the curve with equation`y = x^2 + 1`. The shaded region enclosed by the curve, the y-axis and the line `y = 5` is rotated through `360^0` about the y-axis. Find the volume obtained.
`(π) ∫ (y -1)dy`
`(π)[(y^2)/2 – y]`
`(π)[(25/2 – 5) – (1/2 -1)] = 8 π (25.1)`
Question 15
A curve has equation `y = x^2 − 2x − 3`. A point is moving along the curve in such a way that at P the y-coordinate is increasing at `4` units per second and the x-coordinate is increasing at `6` units per second. Find the x-coordinate of P.
`(dy)/dx = 2x -2`
`(dy)/dx = 4/6`
`(2x -2) = 4/6`
`x = 4/3`
Question 16
The gradient of a curve at the point `(x, y)` is given by `(dy)/dx = 2(x + 3)^(1/2) − x`. The curve has a stationary point at `(a, 14)`, where `a` is a positive constant.
a. Find the value a.
b. Determine the nature of the stationary point.
c. Find the equation of the curve.
a. `2(a + 3)^(1/2) – a = 0`
`4( a + 3) = a^2-> a^2 – 4a – 12 = 0`
`(a-6)(a+2) -> a = 6`
b. `(d^2y)/dx^2 = (x + 3)^(1/2) – 1`
Sub `a-> (d^2y)/dx^2 = 1/3 – 1 = 2/3 < 0` Maximum
c. `y =frac{ 2(x +3)^(3/2)}{3/2} - 1/2x^2 + C`
Sub `x = a` and `y = 14-> 14 = 4/3(9)^(3/2) – 18 + C`
d. `y = 4/3(x + 3)^(3/2) - 1/2x^2 + 4`
Question 17

The diagram shows part of the curve `y = 8/(x +2)` and the line `2y + x = 8`, intersecting at points A and B. The point C lies on the curve and the tangent to the curve at C is parallel to AB.
a.Find, by calculation, the coordinates of A, B and C. [6]
b.Find the volume generated when the shaded region, bounded by the curve and the line, is rotated through `360^o`about the x-axis. [6]
a.Simultaneous equations `8/(x + 2) = 4 - 1/2x`
`x = 0` or `x = 6` `A(0,4)` and `B(6,1)`
At C `-8/((x + 2)^2) = - 1/2 ->` `C(2,2)`
b.Volume under line `= int(-1/2x +4)^2dx = pi [(x^3)/12 - 3x^2 + 16x] = 42pi`
Volume under curve `= pi(8/(x+2))^2dx = pi[-64/(x+2)] = 24pi`
Subtracts and uses `0` to `6-> 18pi`
Question 18

The diagram shows part of the curve `y = 6/x`. The points `(1, 6)` and `(3, 2)` lie on the curve. The shaded region is bounded by the curve and the lines `y = 2` and `x = 1`.
a. Find the volume generated when the shaded region is rotated through `360^o` about the y-axis. [5]
b.The tangent to the curve at a point X is parallel to the line `y + 2x = 0`. Show that X lies on the line `y = 2x`. [3]
a.Volume `=piintx^2dy =piint36/(y^2)dy`
`= pi[-36/y]`
Uses limits `2` to `6`correctly`->12pi`
Volume of cylinder `= pi xx1^2 xx 4`or `int1^2dy = [y]` from `2` to `6`
Volume `= 12pi - 4pi = 8 π`
b.`(dy)/dx = -6/(x^2)`
`-6/(x^2) = -2 ->x =sqrt 3`
`y = 6/sqrt3 = 2sqrt3` Lies on `y = 2x`
Question 19
The equation of a curve is such that `(dy)/dx = 3x^(1/2) −3x^(-1/2)`. It is given that the point `(4, 7)` lies on the curve. Find the equation of the curve. [4]
`(y) = (3x^(3/2))/(3/2) - (3x^(1/2))/(1/2) + (c)`
`7 = 16 - 12 + c`
`y = 2x^(3/2) - 6x^(1/2) + 3`
Question 20

The diagram shows part of the curve with equation `y = x^3 − 2bx^2 + b^2x` and the line OA, where A is the maximum point on the curve. The x-coordinate of A is a and the curve has a minimum point at `(b, 0)`, where a and b are positive constants.
a.Show that `b = 3a`. [4]
b.Show that the area of the shaded region between the line and the curve is `ka^4`, where k is a fraction to be found. [7]
a.`(dy)/dx = 3x^2 – 4bx + b^2`
`3x^2 – 4bx + b^2 = 0 (3x – b)(x – b) = 0`
`x = b/3 or b`
`a = b/3-> b = 3a`
b.Area under curve `=int (x^3– 6ax^2 + 9a^2x)dx`
`(x^2)/4 – 2ax^3 + (9a^2x^2)/2`
`(a^2)/4 – 2a^4 + (9a^4)/2 = (11a^4)/4`
When `x = a`, `y = a^3 – 6a^3 + 9a^3 = 3a^3`
Area under line `= 1/2a x` `their 4a^3`
Shaded area `= (11a^4)/4 – 2a^4 = (3a^4)/4`
Question 1
A curve with equation `y = f(x)` is such that `f′(x)` `=2x^(-1/3)-x^(1/3)`. It is given that `f (8) = 5`. Find `f(x)`
Question 2
A curve is such that `(dy)/(dx)=frac{6}{(3x-2)^3` and `A (1, −3)` lies on the curve. A point is moving along the curve and at A the y-coordinate of the point is increasing at `3` units per second.
a. Find the rate of increase at A of the x-coordinate of the point.
b. Find the equation of the curve.
Question 3

The diagram shows the curve with equation `y = 9 ( x^(-1/2 )− 4x^(-3/2))`. The curve crosses the x-axis at the point A.
a. Find the x-coordinate of A.
b. Find the equation of the tangent to the curve at A.
c. Find the x-coordinate of the maximum point of the curve.
d. Find the area of the region bounded by the curve, the x-axis and the line `x=9`.
Question 4
The equation of a curve is `y = 2sqrt( 3x +4) − x`.
a. Find the equation of the normal to the curve at the point `(4, 4)`, giving your answer in the form `y = mx + c`
b. Find the coordinates of the stationary point
c. Determine the nature of the stationary point
d. Find the exact area of the region bounded by the curve, the x-axis and the lines `x = 0` and `x = 4`
Question 5

The diagram shows part of the curve with equation `y^2 = x − 2` and the lines `x = 5` and `y = 1`. The shaded region enclosed by the curve and the lines is rotated through `360°` about the x-axis. Find the volume obtained.
Question 6
The gradient of a curve is given by `(dy)/dx = 6(3x – 5)^3 − kx^2` , where `k` is a constant. The curve has a stationary point at `(2, −3.5)`.
a. Find the value of `k`
b. Find the equation of the curve
c. Find `(d^2y)/dx^2`
d. Determine the nature of the stationary point `(2, -3.5)`
Question 7

The diagram shows part of the curve with equation `y = x^(1/2) + k^(2x^(-1/2))`, where `k` is a positive constant.
a. Find the coordinates of the minimum point of the curve, giving your answer in terms of `k`.
The tangent at the point on the curve where `x = 4k^2` intersects the y-axis at P.
b. Find the y-coordinate of P in terms of `k`.
The shaded region is bounded by the curve, the x-axis and the lines `x = 9/4k^2` and `x = 4k^2`.
c. Find the area of the shaded region in terms of `k`.
Question 8
A curve has equation `y = f'(x)`, and it is given that `f'(x) = 2x^2 – 7 – 4/(x^2)`.
a. Given that `f(1) = –1/3` , find `f(x)`.
b. Find the coordinates of the stationary points on the curve.
c. Find `f''(x)`
d. Hence, or otherwise, determine the nature of each of the stationary points.
Question 9
a. Find `int_1^oofrac{1}{(3x-2)^(3/2)}dx`
b.

The diagram shows the curve with equation `y = 1/(3x-2)^(3/2)`. The shaded region is bounded by the curve, the x-axis and the lines `x = 1` and `x = 2`. The shaded region is rotated through `360^o` about the x-axis.
Find the volume of revolution.
The normal to the curve at the point `(1, 1)` crosses the y-axis at the point A.
c. Find the y-coordinate of A.
Question 10
A curve is such that `(dy)/dx= 8/((3x + 2)^2`. The curve passes through the point `(2, 5_3^2)`. Find the equation of the curve.
Question 11

The diagram shows the line `x=5/2`, part of the curve `y = 1/2 x + 7/10 − 1/((x -2)^(1/3))` and the normal to the curve at the point A `(3, 6/5)`.
a. Find the x-coordinate of the point where the normal to the curve meets the x-axis.
b. Find the area of the shaded region, giving your answer correct to `2` decimal places.
Question 12

The diagram shows the curves with equations `y = y = x^(-1/2)` and `y = 5/2 - x^(1/2)` . The curves intersect at the points A `(1/4 , 2)` and B `(4, 1/2)`.
a. Find the area of the region between the two curves.
b. The normal to the curve `y = y = x^(-1/2)` at the point `(1, 1)` intersects the y-axis at the point `(0, p)`.
Find the value of `p`.
Question 13
A curve has equation`y = f(x)` and it is given that `f'(x) = (1/2x + k)^-2 – (1 + k)^-2`, where `k` is a constant. The curve has a minimum point at `x =2`.
a. Find `f′′(x)` in terms of `k` and `x`, and hence find the set of possible values.
b. It is now given that `k = −3` and the minimum point is at `(2, 3 1/2)`. Find `f(x)`.
c. Find the coordinates of the other stationary point and determine its nature.
Question 14

The diagram shows part of the curve with equation`y = x^2 + 1`. The shaded region enclosed by the curve, the y-axis and the line `y = 5` is rotated through `360^0` about the y-axis. Find the volume obtained.
Question 15
A curve has equation `y = x^2 − 2x − 3`. A point is moving along the curve in such a way that at P the y-coordinate is increasing at `4` units per second and the x-coordinate is increasing at `6` units per second. Find the x-coordinate of P.
Question 16
The gradient of a curve at the point `(x, y)` is given by `(dy)/dx = 2(x + 3)^(1/2) − x`. The curve has a stationary point at `(a, 14)`, where `a` is a positive constant.
a. Find the value a.
b. Determine the nature of the stationary point.
c. Find the equation of the curve.
Question 17

The diagram shows part of the curve `y = 8/(x +2)` and the line `2y + x = 8`, intersecting at points A and B. The point C lies on the curve and the tangent to the curve at C is parallel to AB.
a.Find, by calculation, the coordinates of A, B and C. [6]
b.Find the volume generated when the shaded region, bounded by the curve and the line, is rotated through `360^o`about the x-axis. [6]
Question 18

The diagram shows part of the curve `y = 6/x`. The points `(1, 6)` and `(3, 2)` lie on the curve. The shaded region is bounded by the curve and the lines `y = 2` and `x = 1`.
a. Find the volume generated when the shaded region is rotated through `360^o` about the y-axis. [5]
b.The tangent to the curve at a point X is parallel to the line `y + 2x = 0`. Show that X lies on the line `y = 2x`. [3]
Question 19
The equation of a curve is such that `(dy)/dx = 3x^(1/2) −3x^(-1/2)`. It is given that the point `(4, 7)` lies on the curve. Find the equation of the curve. [4]
Question 20

The diagram shows part of the curve with equation `y = x^3 − 2bx^2 + b^2x` and the line OA, where A is the maximum point on the curve. The x-coordinate of A is a and the curve has a minimum point at `(b, 0)`, where a and b are positive constants.
a.Show that `b = 3a`. [4]
b.Show that the area of the shaded region between the line and the curve is `ka^4`, where k is a fraction to be found. [7]