Algebra

Solve the equation `|x^2-14|=11`.

`x^2-14=11` or `x^2-14=-11`

`x^2=25` or `x^2=3`

`x=+-5` or `x=+-sqrt3`

Solve the inequality `|2x-3|<|2-x|`.

Sketch the graphs of `y=|2x-3|` and `y=|2-x|`

Graphs intesect where: `|2x-3|=|2-x|`

`(2x-3)^2=(2-x)^2`

`x=5/3`, `x=1`

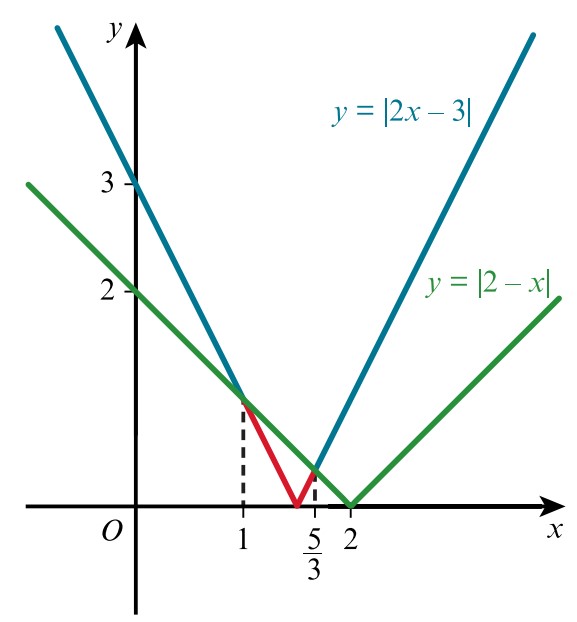
The graph of `y=|2x-3|` lies below the graph of `y=|2-x|` when:

`1< x <5/3`

The polynomial `ax^3-13x^2-41x-2a`, where `a` is a constant, is denoted by `p(x)`

(a) Given `x-4` is a factor of `p(x)`, find the value of `a`.

(b) When `a` has this value, factorise `p(x)` completely.

(a)

`x-4` is a factor of `p(x)`, so `p(4)=0`

`a(4)^3-13(4)^2-41(4)-2a=0`

`a=6` 

(b)

Substituting `a=6` into `p(x)`:

`p(x)=6x^3-13x^2-41x-12`

`x-4` is a factor, using long division:

`p(x)=6x^3-13x^2-41x-12=(x-4)(6x^2+11x+3)`

`=(x-4)(3x+1)(2x+3)`

The polynomial `6x^3-23x^2-38x+15` is denoted by `f(x)`. 

(a) Show that `(x-5)` is a factor of `f(x)` and hence factorise `f(x)` completely. 

(b) Write down the roots of `f(|x|)=0`.

(a)

`f(5)=0`

Hence `x-5` is a factor

Using long division

`f(x)=6x^3-23x^2-38x+15=(x-5)(6x^2+7x-3)`

`=(x-5)(3x-1)(2x+3)` 

(b)

`f(|x|)=0` 

So `(|x|-5)(3|x|-1)(2|x|+3)=0`

`x=±5` or `x=±13` (Reject `|x|=-3/2`)

The polynomial `x^3-5x^2+ax+b` is denoted by `f(x)`. It is given that `(x+2)` is a factor of `f(x)` and that when `f(x)` is divided by `(x-1)` the remainder is `-6`. Find the value of a and the value of `b`.

`x+2` is a factor so `f(-2)=0`

Substituting `x=-2` into `f(x)` and simplify

`2a-b=-28`

`f(x)` is divided by `x-1` the remainder is `-6`

Hence `f(1)=-6`

Substituting `x=1` and simplify

`a+b=-2`

Solve system equations

`a=-10` and `b=8`

The polynomial `x^3-5x^2+7x-3` is denoted by `p(x)`. 

(a) Find the quotient and remainder when `p(x)` is divided by `(x^2-2x-1)`.

(b) Use the factor theorem to show that `(x-3)` is a factor of `p(x)`. 

(a)

Quotient `= x-3`

Remainder `= 2x-6`

(b)

Substituting `x=3` into `p(x)`

Hence find `p(3)=0`

So `x-3` is a factor by theorem

 The polynomial `4x^4+4x^3-7x^2-4x+8` is denoted by `p(x)`. 

(a) Find the quotient and remainder when `p(x)` is divided by `(x^2-1)`.

(b) Hence solve the equation `4x^4+4x^3-7x^2-4x+8=0`.

(a)

Quotient `= 4x^2+4x-3` 

Remainder `= 5`

(b)

`4x^4+4x^3-7x^2-4x+8=(x^2-1)(4x^2+4x-3)+5` 

`4x^4+4x^3-7x^2-4x+3=(x^2-1)(4x^2+4x-3)`

`=(x-1)(x+1)(2x+3)(2x-1)` 

Solution are `x=1`, `-1`, `-32`, `12`.

The polynomial `x^4-48x^2-21x-2` is denoted by `f(x)`.

(a) Find the value of the constant `k` for which `f(x)=(x^2+kx+2)(x^2-kx-1)`. 

(b) Hence solve the equation `f(x)=0`. Give your answers in exact form.

(a)

`f(x)=x^4-48x^2-21x-2` 

`=(x^2+kx+2)(x^2-kx-1)`

`=x^4+(-k+k)x^3+(1-k^2+2)x^2+(-k-2k)x-2`

Compare the coefficients: `k=7` 

(b)

Substituting `k=7`

`x^2+7x+2=0` or `x^2-7x-1=0` 

`x=frac{-7±sqrt41}{2}` or `x=frac{7±sqrt53}{2}`

The polynomial `2x^4+3x^3-12x^2-7x+a` is denoted by `p(x)`. 

(a) Given that `(2x-1)` is a factor of `p(x)`, find the value of `a`. 

(b) When `a` has this value, verify that `(x+3)` is also a factor of `p(x)` and hence factorise `p(x)` completely.

(a)

`(2x-1)` is a factor of `p(x)` so `p(1/2)=0`

Hence find `a=6` 

(b)

Substituting `a=6` into `p(x)` and calculate `p(3)` 

Hence `p(3)=0` 

So `x-3` is also a factor

Using long division to divide `p(x)` by `2x-1` and `x-3` or

`(2x-1)(x-3)=(2x^2+5x-3)`

`2x^4+3x^3-12x^2-7x+6=(2x^2+5x-3)(x^2-x-2)`

`=(2x-1)(x-3)(x-2)(x+1)` 

The polynomial `3x^3+ax^2-36x+20` is denoted by `p(x)`.

(a) Given that `(x-2)` is a factor of `p(x)`, find the value of `a`. 

(b) When `a` has this value, solve the equation `p(x)=0`.

(a)

`(x-2)` is a factor of `p(x)` so `p(2)=0`

Hence find `a=7`

(b)

`p(x)=3x^3+7x^2-36x+20` 

Using long division to divide `p(x)` by `x-2`

`p(x)=3x^3+7x^2-36x+20=(x-2)(3x^2+13x-10)` 

`=(x-2)(3x-2)(x+5)` 

So `x=2`, `2/3`, `-5`

 The polynomial `2x^3+5x^2-7x+11` is denoted by `f(x)`. 

(a) Find the remainder when `f(x)` is divided by `(x-2)`. 

(b) Find the quotient and remainder when `f(x)` is divided by `(x^2-4x+2)`.

(a)

`f(2)=33`

So the remainder `= 33`

(b)

Using long division

Quotient `= 2x+13`

Remainder `= 41x-15`

The polynomial `ax^3+bx^2-x+12` is denoted by `p(x)`.

(a) Given that `(x-3)` and `(x+1)` are factors of `p(x)`, find the value of `a` and the value of `b`. 

(b) When `a` and `b` take these values, find the other linear factor of `p(x)`.

(a) 

`(x-3)` and `(x+1)` are factors of `p(x)` so `p(3)=p(-1)=0` 

Substituting `x=3` and `x=-1` then simplify

`3a-b=-1` and `a-b=13`

Solve system equations: `a=3` and `b=-10`

(b)

`(x-3)(x+1)=(x^2-2x-3)` 

Using long division

`p(x)=3x^3-10x^2-x+12=(x^2-2x-3)(3x-4)` 

`=(x-3)(x+1)(3x-4)` 

`3x-4` is the remaining linear factor of `p(x)`.

The polynomial `6x^3+x^2+ax-10`, where `a` is a constant, is denoted by `P(x)`. It is given that when `P(x)` is divided by `(x+2)` the remainder is `-12`. 

(a) Find the value of `a` and hence verify that `(2x + 1)` is a factor of `P(x)`.

(b) When `a` has this value, solve the equation `P(x)=0`.

(a)

`(x+2)` is a factor of `P(x)` so `P(-2)=-12`

Substituting `x=-2`

Hence find `a=-21`

Calculate `P(-12)=0`, so `(2x + 1)` is a factor of `P(x)`

(b)

Using long division by `2x+1`

`P(x)=(2x+1)(3x^2-x-10)=(2x+1)(3x+5)(x-2)`

So `x=-1/2`, `-5/3`, 2

The polynomial `2x^3+ax^2+bx+6` is denoted by `p(x)`. 

a Given that `(x+2)` and `(x-3)` are factors of `p(x)`, find the value of `a` and the value of `b`.

b When `a` and `b` take these values, factorise `p(x)` completely.

(a)

`(x+2)` and `(x-3)` are factors of `p(x)` so `p(-2)=p(3)=0`

Substituting `x=-2` and `x=3` then simplify

`2a-b=5` and `3a+b=-20` 

Solve system equations: `a=-3` and `b=-11`

(b)

Using long division by `(x+2)(x-3)=(x^2-x-6)`

`p(x)=(x^2-x-6)(2x-1)=(x-3)(x+2)(2x-1)`

The polynomials `P(x)` and `Q(x)` are defined as: 

`P(x)=x^3+ax^2+b` and `Q(x)=x^3+bx+a`.

It is given that `(x-2)` is a factor of `P(x)` and that when `Q(x)` is divided by `(x+1)` the remainder is `-15`. 

(a) Find the value of `a` and the value of `b`. 

(b) When `a` and `b` take these values, find the least possible value of `P(x)-Q(x)` as `x` varies.

(a)

`x-2` is a factor of `P(x)`, so `P(2)=0`

Substituting `x=2` into `P(x)` and simplify: `4a+b=-8`

`Q(x)` is divided by `(x+1)` the remainder is `-15`

So `Q(-1)=-15`

Substituting `x=-1` into `Q(x)` and simplify: `a+b=-14`

Solve system equations: `a=2` and `=-16`

(b)

Using the values `a` and `b` from part (a)

`P(x)-Q(x)=18x^2-18`

Minimum value when `x=0` and minimum `= -18`

The polynomial `5x^3-13x^2+17x-7` is denoted by `p(x)`. 

(a) Find the quotient when `p(x)` is divided by `(x-1)`, and show that the remainder is `2`.

(b) Hence show that the polynomial `5x^3-13x^2+17x-7=0` has exactly one real root.

(a)

Using long division

Quotient `= 5x^2-8x+9`

Remainder `= 2`

(b)

Using the result from part (a)

`5x^3-13x^2+17x-7=(x-1)(5x^2-8x+9)+2` 

`5x^3-13x^2+17x-9=(x-1)(5x^2-8x+9)=0` 

`x-1=0` or `5x^2-8x+9=0` (`∆=-116 < 0`) 

So `x=1`

The polynomial `2x^3-9x^2+ax+b`, where `a` and `b` are constants, is denoted by `f(x)`. It is given that `(x+2)` is a factor of `f(x)`, and that when `f(x)` is divided by `(x+1)` the remainder is `30`. 

(a) Find the value of a and the value of `b`.  

(b) When `a` and `b` have these values, solve the equation `f(x)=0`.

(a)

`(x+2)` is a factor of `f(x)` so `f(-2)=0`

Substituting `x=-2` and simplify: `2a-b=-52`

`f(x)` is divided by `(x+1)` the remainder is `30`

Substituting `x=-1` into `f(x)` and `f(-1)=30`: `a-b=-41`

Solve system equations: `a=-11` and `b=30`

(b)

Using the values `a` and `b` from part (a) and long division:

`f(x)=2x^3-9x^2-11x+30=(x+2)(2x^2-13x+15)=(x+2)(2x-3)(x-5)`

So `x=-2`, `3/2`, `5`.

The polynomial `x^3+3x^2+4x+2` is denoted by `f(x)`. 

(a) Find the quotient and remainder when `f(x)` is divided by `x^2+x-1`.

(b) Use the factor theorem to show that `(x+1)` is a factor of `f(x)`.

(a)

Using long division by `x^2+x-1`

Quotient `= x+2`

Remainder `= 3x+4`

(b)

`f(x)=x^3+3x^2+4x+2`

`f(-1)=0`

So `(x+1)` is a factor of `f(x)`

The polynomial `4x^3+ax^2+9x+9`, where `a` is a constant, is denoted by `p(x)`. It is given that when `p(x)` is divided by `(2x-1)` the remainder is `10`. 

(a) Find the value of `a` and hence verify that `(x-3)` is a factor of `p(x)`. 

(b) When `a` has this value, solve the equation `p(x)=0`.

(a)

`p(x)` is divided by `(2x-1)` the remainder is `10` so `p(1/2)=10`

Substituting `x=1/2` and simplify: `a=-16`

Substituting `a=-16` into `p(x)`

`p(x)=4x^3-16x^2+9x+9`

`p(3)=0` 

So `(x-3)` is a factor of `p(x)`

(b)

Using long division by `x-3`

`p(x)=4x^3-16x^2+9x+9=(x-3)(4x^2-4x-3)=(x-3)(2x+1)(2x-3)` 

`(x-3)(2x+1)(2x-3)=0`

So `x=3`, `-1/2`, `3/2`

The polynomial `ax^3-5x^2+bx+9`, where `a` and `b` are constants, is denoted by `p(x)`. It is given that `(2x+3)` is a factor of `p(x)`, and that when `p(x)` is divided by `(x+1)` the remainder is `8`. 

(a) Find the values of `a` and `b`. 

(b) When `a` and `b` have these values, factorise `p(x)` completely.

(a)

`(2x+3)` is a factor of `p(x)` so `p(-3/2)=0` 

Substituting `x=-3/2` and simplify: `9a+4b=-6`

`p(x)` is divided by `(x+1)` the remainder is `8` so `p(-1)=8`

Hence find: `a+b=-4`

Solve system equations: `a=2` and `b=-6`

(b)

Using long division by `2x+3`

`2x^3-5x^2-6x+9=(2x+3)(x^2-4x+3)=(2x+3)(x-3)(x-1)`