A Level Mathematics - Questionbank
Logarithmic and exponential functions explores the properties and applications of logarithmic and exponential functions, including their use in solving equations and modeling growth and decay.
Question 1
Solve the inequality `2^x>7`, giving your answer in terms of logarithms.
Easy
Mark as Complete
Mark Scheme
Question 2
Given that `lnp =2lnq-ln(3+q)` and that `q>0`, express `p` in terms of `q` not involving logarithms.
Easy
Mark as Complete
Mark Scheme
Question 3
Solve the inequality `3.2^(3x+2) <8`, giving your answer in terms of logarithms
Easy
Mark as Complete
Mark Scheme
Question 4
Use logarithms to solve the equation
`5^(x+3)=7^(x-1)`
Giving the answer correct to `3` significant figures.
Easy
Mark as Complete
Mark Scheme
Question 5
Solve the equation `6(4^x)-11(2^x)+4=0`, giving your answers for `x` in terms of logarithms where appropriate.
Medium
Mark as Complete
Mark Scheme
Question 6
Solve the equation `ln(5x+4) =2lnx +ln6`.
Medium
Mark as Complete
Mark Scheme
Question 7
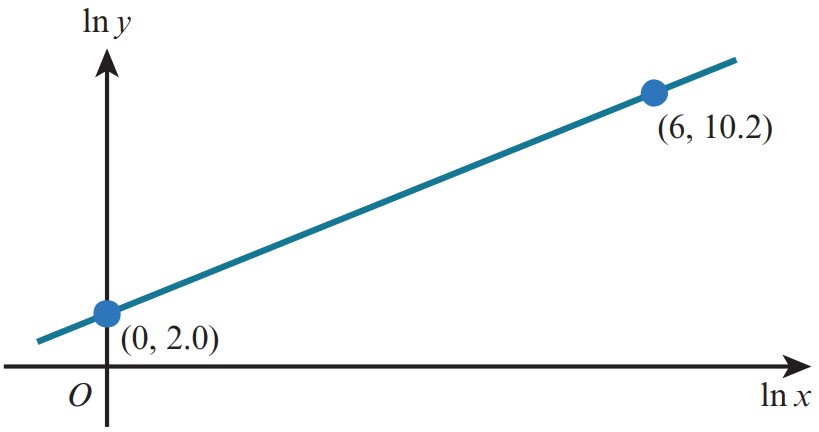
The variables `x` and `y` satisfy the equation `y=Kx^m`, where `K` and `m` are constants. The graph of `ln y` against `ln x` is a straight line passing through the points `(0, 2.0)` and `(6, 10.2)`, as shown in the diagram. Find the values of `K` and `m`, correct to `2` decimal places.
Hard
Mark as Complete
Mark Scheme
Question 8
a) Given that `y=2^x`, show that the equation: `2^x+3(2^-x)=4` can be written form `y^2-4y+3=0`.
b) Hence solve the equation `2^x+3(2^-x)=4` giving the values of `x` correct to `3` significant figures where appropriate.
Hard
Mark as Complete
Mark Scheme
Question 9
Given that `(1.2)^x=6^y`, use logarithms to find the value of `x/y` correct to `3` significant figures.
Easy
Mark as Complete
Mark Scheme
Question 10
The polynomial `f(x)` is defined by: `f(x)=12x^3+25x^2-4x-12`.
a) Show that `f(-2)=0` and factorise `f(x)` completely.
b) Given that `12(27^y)+25(9^y)-4(3^y)-12=0`, state the value of `3^y` and hence find y correct to `3` significant figures.
Hard
Mark as Complete
Mark Scheme
Question 11
Solve the equation `|4-2^x|=10`, giving your answer correct to `3` significant figures.
Medium
Mark as Complete
Mark Scheme
Question 12
Use logarithms to solve the equation `e^x=3^(x-2)`, giving your answer correct to `3` decimal places.
Easy
Mark as Complete
Mark Scheme
Question 13
Using the substitution `u=3^x`, solve the equation `3^x+3^(2x)=3^(3x)` giving your answer correct to `3` significant figures.
Medium
Mark as Complete
Mark Scheme
Question 14
The variables x and y satisfy the equation `5^y=3^(2x-4).`
a) By taking natural logarithms, show that the graph of y against `x` is a straight line and find the exact value of the gradient of this line.
b) This line intersects the x-axis at P and the y-axis at `Q`. Find the exact coordinates of the midpoint of PQ.
Hard
Mark as Complete
Mark Scheme
Question 15
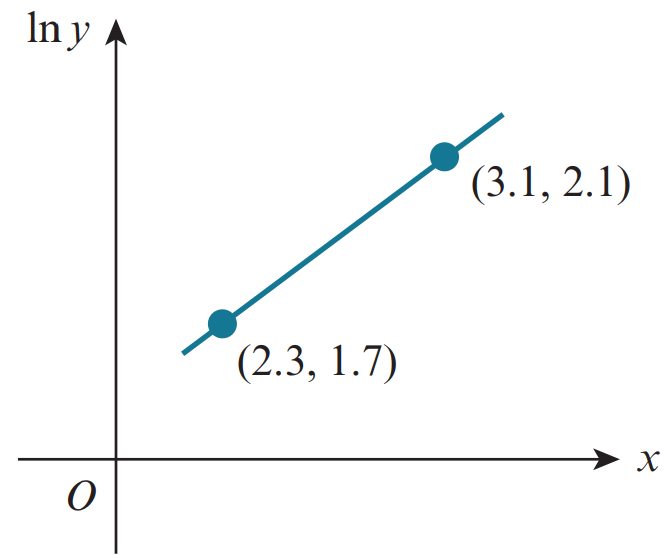
The variables `x` and `y`satisfy the equation `y=K(b^x)`, where `K` and `b` are constants. The graph of `ln y` against `x` is a straight line passing through the points `(2.3, 1.7)` and `(3.1, 2.1)`, as shown in the diagram. Find the values of `K` and `b`, correct to `2` decimal places.
Hard
Mark as Complete
Mark Scheme
Question 16
Variables x and y are related so that, when y is plotted on the vertical axis and x is plotted on the horizontal axis, a straight-line graph passing through the points `(2, 5)` and `(6, 11)` is obtained.
a) Express `y` in terms of `x`.
b) Express `y`in terms of `x`, giving your answer in the form`y=a(10^(bx))`.
Medium
Mark as Complete
Mark Scheme
Question 17
The variables x and y satisfy the equation `5^(2y)=3^(2x+1)`. By taking natural logarithms, show that the graph of `ln y` against `ln x` is a straight line, and find the exact value of the gradient of this line and state the coordinates of the point at which the line cuts the y-axis. [5]
Medium
Mark as Complete
Mark Scheme
Question 18
Solve `ln (2x+1)<= ln (x+4)` .
Medium
Mark as Complete
Mark Scheme
Question 19
Solve `2ln (3-e^(2x))=1` , giving your answer correct to `3` significant figures.
Medium
Mark as Complete
Mark Scheme
Question 20
Prove that the solution to the inequality `3^(2x-1)xx2^(1-3x)≥5` is `x≥frac{log (15/2)}{ log (9/8)}`
Medium
Mark as Complete
Mark Scheme
Question 1
Solve the inequality `2^x>7`, giving your answer in terms of logarithms.
`2^x>7`
`log 2^x > log 7`
`x log 2 > log 7`
`x>frac{log7}{log2}`
Question 2
Given that `lnp =2lnq-ln(3+q)` and that `q>0`, express `p` in terms of `q` not involving logarithms.
`lnp =2lnq -ln(3+q)`
`lnp =lnq^2 -ln(3+q)`
`lnlnp =lnln(frac{q^2}{3+q})`
`p=frac{q^2}{3+q}`
Question 3
Solve the inequality `3.2^(3x+2) <8`, giving your answer in terms of logarithms
`3.2^(3x+2) <8`
`3.(2^2)(2^(3x))<8`
`8^x<2/3`
`log8^x`
`x log 8 < log frac{2}{3}`
`x< frac{log frac{2}{3}}{log 8}`
Question 4
Use logarithms to solve the equation
`5^(x+3)=7^(x-1)`
Giving the answer correct to `3` significant figures.
`5^(x+3)=7^(x-1)`
`log(5^(x+3)) =log7^(x-1)`
`(x+3)log5 =(x-1)log7`
`xlog5 +3log5 =xlog7 -log7`
`x=frac{3log5 +log7}{log7 -log5} =20.1`
Question 5
Solve the equation `6(4^x)-11(2^x)+4=0`, giving your answers for `x` in terms of logarithms where appropriate.
`6(4^x)-11(2^x)+4=0`
`6(2^(2x))-11(2^x)+4=0`
Let `u=2^x`
`6u^2-11u+4=0`
`(3u-4)(2u-1)=0`
`u=4/3` or `u=1/2`
`2^x=4/3` or `2^x=1/2`
`x=4/3` or `x=1/2`
`x=frac{2log2 -log3}{log2}` or `x=-1`
Question 6
Solve the equation `ln(5x+4) =2lnx +ln6`.
`ln (5x+4) =2ln x +ln 6`
`ln (5x+4) =ln x2 +ln 6`
`ln (5x+4) =ln (x2+6)`
`5x+4=x^2+6`
`x=4/3` or `x=-1/2`
But `x>0` in logarithms
So `x=4/3`
Question 7

The variables `x` and `y` satisfy the equation `y=Kx^m`, where `K` and `m` are constants. The graph of `ln y` against `ln x` is a straight line passing through the points `(0, 2.0)` and `(6, 10.2)`, as shown in the diagram. Find the values of `K` and `m`, correct to `2` decimal places.
`y=Kx^m`
`ln y =ln K +ln x^m`
`ln y =mln x +ln K`
`Y=mX+c`
`Y=ln y`
`m=m`
`X=ln x`
`c=ln K`
From the diagram:
Gradient `= m=1.37`
`y-"intercept"=2=c`
`ln K =2`
`K=e^2=7.39`
Question 8
a) Given that `y=2^x`, show that the equation: `2^x+3(2^-x)=4` can be written form `y^2-4y+3=0`.
b) Hence solve the equation `2^x+3(2^-x)=4` giving the values of `x` correct to `3` significant figures where appropriate.
a)
`y=2^x`
`2^x+3(2^-x)=4`
`2^x+3(2^x)^-1=4`
`y+3y^-1=4`
`y+3/y=4`
`y^2-4y+3=0`
b)
`y^2-4y+3=0`
`y=1` or `y=3`
`2^x=1` or `2^x=3`
`x=0` or `x=1.58`
Question 9
Given that `(1.2)^x=6^y`, use logarithms to find the value of `x/y` correct to `3` significant figures.
`(1.2)^x=6^y`
`ln (1.2)^x =ln 6^y`
`xln 1.2 =yln 6`
`x/y=frac{ln 6}{ ln 1.2} =9.38`
Question 10
The polynomial `f(x)` is defined by: `f(x)=12x^3+25x^2-4x-12`.
a) Show that `f(-2)=0` and factorise `f(x)` completely.
b) Given that `12(27^y)+25(9^y)-4(3^y)-12=0`, state the value of `3^y` and hence find y correct to `3` significant figures.
a)
`f(x)=12x^3+25x^2-4x-12`
`f(-2)=0`
`x+2` is a factor
Using long division
`f(x)=(x+2)(12x^2+x-6)=(x+2)(3x-2)(4x+3)`
b)
`12(27^y)+25(9^y)-4(3^y)-12=0`
`12(3^y)^3+25(3^y)^2-4(3^y)-12=0`
`f(x)=0→(x+2)(3x-2)(4x+3)=0`
`x=-2`, `2/3`, `-4/3`
So `3^y=-2` or `3^y=2/3` or `3^y=-4/3` but `3^y>0`
So `3^y=2/3→y=log_3(2/3) =-0.369`
Question 11
Solve the equation `|4-2^x|=10`, giving your answer correct to `3` significant figures.
`|4-2^x|=10`
`4-2^x=10` or `4-2^x=-10`
`2^x=-6` or `2^x=14` but `2^x>0`
`x=14 =3.81`
Question 12
Use logarithms to solve the equation `e^x=3^(x-2)`, giving your answer correct to `3` decimal places.
`e^x=3^(x-2)`
`ln e^x =ln 3^(x-)2`
`x=(x+2)ln 3`
`x=(2ln 3)/( ln 3 -1)=22.281`
Question 13
Using the substitution `u=3^x`, solve the equation `3^x+3^(2x)=3^(3x)` giving your answer correct to `3` significant figures.
`3^x+3^(2x)=3^(3x)`
`3^x+(3x)^2=(3x)^3`
Let `u=3^x`
`u+u^2=u^3`
`u(u^2+u+1)=0`
`u=0, frac{1+sqrt5}{2}, frac{1-sqrt5}{2}` but `u=3^x>0`
`3^x=frac{1+sqrt5}{2}`
`x=frac{1+sqrt5}{2} =0.438`
Question 14
The variables x and y satisfy the equation `5^y=3^(2x-4).`
a) By taking natural logarithms, show that the graph of y against `x` is a straight line and find the exact value of the gradient of this line.
b) This line intersects the x-axis at P and the y-axis at `Q`. Find the exact coordinates of the midpoint of PQ.
a)
`5^y=3^(2x-4)`
`ln 5^y =ln 3^(2x-4)`
`yln 5 =(2x-4)ln 3`
`y=(frac{2ln 3}{ln 5}) x-frac{4ln 3}{ ln 5}`
`Y=mX+c`
`Y=y`
`m=-frac{4ln 3}{ ln 5 }`
Gradient `= frac{2ln 3}{ ln 5}`
b)
`y=frac{2ln 3}{ ln 5} x-frac{4ln 3}{ ln 5}`
When`x=0→y=-frac{4ln 3}{ ln 5}`
When `y=0→x=2`
Point P is `(2, 0)`
Point Q is `(0, -frac{4ln 3}{ ln 5})`
Midpoint `(0, -frac{2ln 3}{ ln 5})`
Question 15

The variables `x` and `y`satisfy the equation `y=K(b^x)`, where `K` and `b` are constants. The graph of `ln y` against `x` is a straight line passing through the points `(2.3, 1.7)` and `(3.1, 2.1)`, as shown in the diagram. Find the values of `K` and `b`, correct to `2` decimal places.
`y=K(b)^x`
`ln y =ln K +ln b^x`
`ln y =xln b +ln K`
`Y=mX+c`
`Y=ln y`
`m=ln b`
`X=x`
`c=ln K`
From the diagram:
Gradient `= m = 1/2`
`ln b =1/2`
`b=e^(1/2)=1.65`
Line passes through `(2.3, 1.7)`
`Y=mX+c`
`1.7=1/2(2.3)+c`
`c=0.55`
`ln K =0.55`
`K=e^0.55`
Question 16
Variables x and y are related so that, when y is plotted on the vertical axis and x is plotted on the horizontal axis, a straight-line graph passing through the points `(2, 5)` and `(6, 11)` is obtained.
a) Express `y` in terms of `x`.
b) Express `y`in terms of `x`, giving your answer in the form`y=a(10^(bx))`.
a)
`y =mx+c`
`m=(11-5)/(6-2)=3/2`
`y =3/2x+c`
`5=3/2×2+c`
`c=2`
`y =3/2x+2`
b)
`y =3/2x+2`
`y=10^(3/2x+2`
`y=100×10^(3/2x`
Question 17
The variables x and y satisfy the equation `5^(2y)=3^(2x+1)`. By taking natural logarithms, show that the graph of `ln y` against `ln x` is a straight line, and find the exact value of the gradient of this line and state the coordinates of the point at which the line cuts the y-axis. [5]
`5^(2y)=3^(2x+1)`
`ln 5^(2y) =ln 3^(2x+1)`
`2yln 5 =(2x+1)ln 3`
`y=(frac{ln 3}{ ln 5}) x+frac{ln 3}{ 2ln 5 }`
Gradient `= frac{ln 3}{ ln 5}`
Crosses `y`-axis at `(0, frac{ln 3}{ 2ln 5})`
Question 18
Solve `ln (2x+1)<= ln (x+4)` .
Solve `ln (2x+1)<= ln (x+4)`
`2x+1<= x+4`
`x≤3`
But `2x+1>0`and `x+4>0` giving `x> -1/2`
So `-1/2 < x <= 3`
Question 19
Solve `2ln (3-e^(2x))=1` , giving your answer correct to `3` significant figures.
`2ln (3-e^(2x))=1`
`ln (3-e^(2x))=1/2`
`3-e^(2x)=e^(1/2)`
`e^(2x)=3-e^(1/2)`
`2x=ln( 3-e^(1/2))`
`x=1/2ln( 3-e^(1/2))`
Question 20
Prove that the solution to the inequality `3^(2x-1)xx2^(1-3x)≥5` is `x≥frac{log (15/2)}{ log (9/8)}`
`3^(2x-1)xx2^(1-3x)≥5`
`log 3^(2x-1) +log 2^(1-3x)>= log 5`
`(2x-1)log 3 +(1-3x)log 2>= log 5`
`2xlog 3 -log 3 +log 2 -3xlog 2 ≥5`
`x≥frac{log (15/2)}{ log (9/8)}`
Question 1
Solve the inequality `2^x>7`, giving your answer in terms of logarithms.
Question 2
Given that `lnp =2lnq-ln(3+q)` and that `q>0`, express `p` in terms of `q` not involving logarithms.
Question 3
Solve the inequality `3.2^(3x+2) <8`, giving your answer in terms of logarithms
Question 4
Use logarithms to solve the equation
`5^(x+3)=7^(x-1)`
Giving the answer correct to `3` significant figures.
Question 5
Solve the equation `6(4^x)-11(2^x)+4=0`, giving your answers for `x` in terms of logarithms where appropriate.
Question 6
Solve the equation `ln(5x+4) =2lnx +ln6`.
Question 7

The variables `x` and `y` satisfy the equation `y=Kx^m`, where `K` and `m` are constants. The graph of `ln y` against `ln x` is a straight line passing through the points `(0, 2.0)` and `(6, 10.2)`, as shown in the diagram. Find the values of `K` and `m`, correct to `2` decimal places.
Question 8
a) Given that `y=2^x`, show that the equation: `2^x+3(2^-x)=4` can be written form `y^2-4y+3=0`.
b) Hence solve the equation `2^x+3(2^-x)=4` giving the values of `x` correct to `3` significant figures where appropriate.
Question 9
Given that `(1.2)^x=6^y`, use logarithms to find the value of `x/y` correct to `3` significant figures.
Question 10
The polynomial `f(x)` is defined by: `f(x)=12x^3+25x^2-4x-12`.
a) Show that `f(-2)=0` and factorise `f(x)` completely.
b) Given that `12(27^y)+25(9^y)-4(3^y)-12=0`, state the value of `3^y` and hence find y correct to `3` significant figures.
Question 11
Solve the equation `|4-2^x|=10`, giving your answer correct to `3` significant figures.
Question 12
Use logarithms to solve the equation `e^x=3^(x-2)`, giving your answer correct to `3` decimal places.
Question 13
Using the substitution `u=3^x`, solve the equation `3^x+3^(2x)=3^(3x)` giving your answer correct to `3` significant figures.
Question 14
The variables x and y satisfy the equation `5^y=3^(2x-4).`
a) By taking natural logarithms, show that the graph of y against `x` is a straight line and find the exact value of the gradient of this line.
b) This line intersects the x-axis at P and the y-axis at `Q`. Find the exact coordinates of the midpoint of PQ.
Question 15

The variables `x` and `y`satisfy the equation `y=K(b^x)`, where `K` and `b` are constants. The graph of `ln y` against `x` is a straight line passing through the points `(2.3, 1.7)` and `(3.1, 2.1)`, as shown in the diagram. Find the values of `K` and `b`, correct to `2` decimal places.
Question 16
Variables x and y are related so that, when y is plotted on the vertical axis and x is plotted on the horizontal axis, a straight-line graph passing through the points `(2, 5)` and `(6, 11)` is obtained.
a) Express `y` in terms of `x`.
b) Express `y`in terms of `x`, giving your answer in the form`y=a(10^(bx))`.
Question 17
The variables x and y satisfy the equation `5^(2y)=3^(2x+1)`. By taking natural logarithms, show that the graph of `ln y` against `ln x` is a straight line, and find the exact value of the gradient of this line and state the coordinates of the point at which the line cuts the y-axis. [5]
Question 18
Solve `ln (2x+1)<= ln (x+4)` .
Question 19
Solve `2ln (3-e^(2x))=1` , giving your answer correct to `3` significant figures.
Question 20
Prove that the solution to the inequality `3^(2x-1)xx2^(1-3x)≥5` is `x≥frac{log (15/2)}{ log (9/8)}`