Question 1
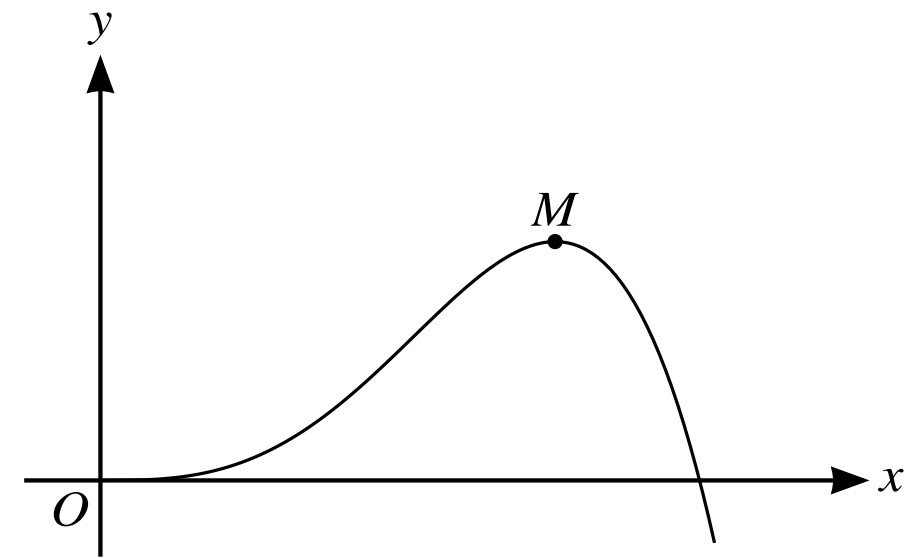
The diagram shows part of the curve with equation `y = x^3cos2x`. The curve has a maximum at the point `M`.
a. Show that the x-coordinate of M satisfies the equation `x = root(3)(1.5x^2cot2x)`.
b. Use the equation in part (a) to show by calculation that the x-coordinate of `M` lies between `0.59` and `0.6`.
c. Use an iterative formula, based on the equation in part (a), to find the x-coordinate of `M` correct to `3` s.f. Given the result of each iteration to `5` s.f.
Medium
Mark as Complete
Mark Scheme
Question 2
It is given that `3sin2theta= costheta` where `θ` is an angle such that `0^o< theta < 90^o`.
a. Find the exact value of `sintheta`.
b. Find the exact value of `sectheta`.
c. Find the exact value of `cos2theta`.
Easy
Mark as Complete
Mark Scheme
Question 3
Solve the equation `7cottheta = 3"cosec"theta` for `0^o < theta < 90^o`.
Medium
Mark as Complete
Mark Scheme
Question 4
Solve the equation
`sec^2theta + tan^2theta = 5tantheta + 4` for `0^o< theta < 180^o`.
Medium
Mark as Complete
Mark Scheme
Question 5
a. Show that `2"cosec"2thetacottheta -= "cosec"^2theta`.
b. Solve the equation `2 "cosec" phi cot frac{1}{2}phi + "cosec"1/2phi = 12` for `-360^o < phi < 360^o`. Show all necessary working.
Medium
Mark as Complete
Mark Scheme
Question 6
a.
i. Express `4sin theta + 4 cos theta` in the form `Rsin( theta+a )`, where `R > 0` and `0^o < alpha < 90^o`.
ii. Hence find the smallest positive value of `theta` satisfying the equation `4sintheta + 4costheta = 5`.
b. Solve the equation `4cot2x = 5 + tanx` for `0 < x < pi`, showing all necessary working and giving the answers correct to `2` decimal places.
Medium
Mark as Complete
Mark Scheme
Question 7
a. Showing all necessary working, solve the equation `secalpha"cosec"alpha = 7` for `0^o < alpha < 90^o`.
b. Showing all necessary working, solve the equation `sin(beta + 20^o) + sin(beta - 20^o) = 6cosbeta` for `0^o < beta < 90^o`.
Easy
Mark as Complete
Mark Scheme
Question 8
a. Express `0.`theta`5costheta - 1.2sintheta` in the form `Rcos(theta+alpha )`, where `R > 0` and `0^o< alpha < 90^o`, giving the value of `alpha` correct to `2` decimal places.
b. Hence solve the equation `0.5costheta – 1.2sintheta = 0.8` for `0^o< theta < 360^o`.
c. Determine the greatest and least possible values of `(3 - costheta + 2.4sintheta)^2` as varies.
Easy
Mark as Complete
Mark Scheme
Question 9
Solve the equation `sec^2theta = 3 "cosec"theta` for `0^o< theta < 180^o`.
Easy
Mark as Complete
Mark Scheme
Question 10
a. Use the factor theorem to show that `(2x +3)` is a factor of `8x^3 + 4x^2 - 10x + 3`.
b. Show that the equation `2cos2theta = frac{6costheta -5}{2costheta+1}` can be expressed as `8cos^3theta + 4cos^2theta - 10cos + 3 = 0`.
c. Solve the equation `2cos2theta = frac{6costheta -5}{2costheta+1}` for `0^o< theta < 360^o`.
Medium
Mark as Complete
Mark Scheme
Question 11
a. Given that `tan2thetacottheta = 8`, show that `tan^2theta = 3/4`.
b. Hence solve the equation `tan2thetacottheta = 8` for `0^o< theta < 180^o`.
Easy
Mark as Complete
Mark Scheme
Question 12
a. Express `2costheta + (sqrt5)sintheta` in the form `Rcos( theta - alpha )` where `R > 0` and `0^o< theta < 90^o`, giving the value of `alpha` correct to `2` decimal places.
b. Hence solve the equation `2costheta + (sqrt5)sintheta =1` for `0^o.
Medium
Mark as Complete
Mark Scheme
Question 13
Solve the equation `5costheta(1 + cos2theta) = 4` for `0^o<= theta <= 360^o`.
Easy
Mark as Complete
Mark Scheme
Question 14
Solve the equation `5tan2theta = 4cottheta` for `0^o.
Easy
Mark as Complete
Mark Scheme
Question 15
i.Show that `sin(theta + 60^o) + sin(theta + 120^o) -= sqrt3costheta`.
ii.Hence
a. Find the exact value of `sin105^o + sin165^o`.
b. Solve the equation `sin(theta + 60^o) + sin(theta + 120^o) = sectheta` for `0^o <= theta <= 180^o`.
Medium
Mark as Complete
Mark Scheme
Question 16
The polynomial `p(x)` is defined by
`p(x) = ax^3 + 3x^2 + bx + 12`,
where `a` and `b` are constants. It is given that `(x+3)` is a factor of `p(x)`. It is also given that the remainder is `18` when `p(x)` is divided by `(x+2)`.
a.Find the values of `a` and `b`
b. When `a` and `b` have these values,
Show that the equation `p(x) = 0` has exactly one real root.
c. Solve the equation `p(secy) = 0` for `-180^o< theta < 180^o`.
Hard
Mark as Complete
Mark Scheme
Question 17
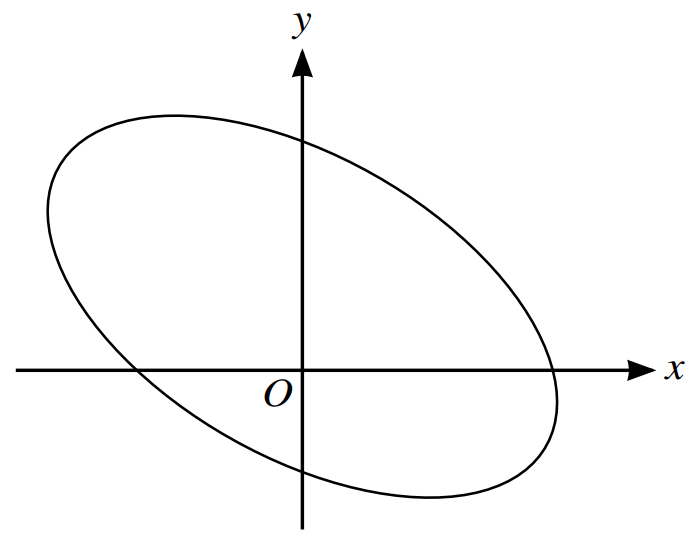
The diagram shows the curve with parametric equations `x = 4sintheta`,`y = 1 + 3cos(theta + pi/6)` for `0<= theta < 2pi`.
a. Show that `(dy)/(dx)` can be expressed in the form `k(1 + sqrt3tantheta)` where the exact value of k is to be determined.
b. Find the equation of the normal to the curve at the point where the curve crosses the positive y – axis. Give your answer in the form `y = mx + c`, where the constants `m` and `c` are exact.
Hard
Mark as Complete
Mark Scheme
Question 18
a. Express `sin2theta(3sectheta + 4"cosec" θ)` in the form `asin theta + bcostheta`, where `a` and `b` integers.
b. Hence express `sin2theta(3sectheta + 4"cosec" θ)` in the form `Rsin(theta + alpha)` where `R > 0` and `0^o< theta < 90^o`.
c. Using the result of part (ii), solve the equation `sin2theta(3sectheta + 4"cosec" θ) = 7` for `0^o <= theta <= 360^o`.
Medium
Mark as Complete
Mark Scheme
Question 19
It is given that `theta` is an acute angle measured in degrees such that
`2sec^2theta + 3tantheta = 22`
a.Find the value of `tantheta`,
b. Use an appropriate formula to find the exact value of `tan(theta + 135^o)`.
Easy
Mark as Complete
Mark Scheme
Question 20
a. Express `8sintheta 15costheta` in the form `Rsin(theta + alpha)`, where `R > 0` and `0^o< alpha < 90^o`. Given that value of `alpha` correct to `2` decimal places.
b. Hence solve the equation `8sintheta + 15costheta = 6` for `0^o <= theta <= 360^o`.
Easy
Mark as Complete
Mark Scheme
Question 1

The diagram shows part of the curve with equation `y = x^3cos2x`. The curve has a maximum at the point `M`.
a. Show that the x-coordinate of M satisfies the equation `x = root(3)(1.5x^2cot2x)`.
b. Use the equation in part (a) to show by calculation that the x-coordinate of `M` lies between `0.59` and `0.6`.
c. Use an iterative formula, based on the equation in part (a), to find the x-coordinate of `M` correct to `3` s.f. Given the result of each iteration to `5` s.f.
a. The equation of the curve is `y = x^3cos2x`.
We need to show that x-coordinate of the maximum point `M` satisfies `x = root(3)(1.5x^2cot(2x))`.
Find the derivative of the function to locate the critical points.
`(dy)/(dx) = 3x^2 2cos2x – 2x^3sin2x`
`(dy)/(dx) = 0`
`3x^2cos2x – 2x^3sin2x = 0`
`cos2x = frac{2xsin(2x)}{3}`
Using the trigonometric identity `cos2x = cot(2x).sin(2x)`, the equation can be rearranged to match the given form: `x=root(3)(1.5x^2cot(2x))`
b. Test the boundary values:
For `x = 0.59`, plug in this value into the curve, we calculate is `0.598`.
For `x = 0.6`, do the same as last x-value, we find out `0.613`.
For `x =0.59`, we get approximately `0.598` and for `x=0.6`, we get approximately `0.613`. These values show that the x-coordinate of `M` lies between `0.59` and `0.6` as required.
c. To find the x-coordinate of `M` using an iterative formula, we use the equation from part (a).
The iterative formula based on the equation is: `x_(n+1) = root(3)(1.5x_n^2cot(2x_n))`.
Start with an initial guess, say `x_0 = 0.6`
Substitute into the iterative formula
`x_1~~0.613`
Use `x_1 = 0.613` → Continue to find `x_2~~0.620`
Use `x_2 = 0.620` → Continue to find `x_3~~0.622`
The x-coordinate converges to `x = 0.623` after `3` `-4` iterations. Therefore, the x- coordinated of `M`, correct to `3` s.f, is: `0.623`.
Question 2
It is given that `3sin2theta= costheta` where `θ` is an angle such that `0^o< theta < 90^o`.
a. Find the exact value of `sintheta`.
b. Find the exact value of `sectheta`.
c. Find the exact value of `cos2theta`.
a. `3sin2theta = costheta` (`sin2theta = 2sinthetacostheta`)
`6 sinthetacostheta = costheta`
`sintheta = 1/6`
b. `sectheta = 1/costheta`
To find `costheta`, we use the Pythagorean identity: `sin^2theta + cos^2theta =1`
Substitute `sintheta = 1/6` into the equation:
`(1/6)^2 + cos^2theta = 1`
Solve out `costheta = sqrt35/ 6 → sectheta = 6/sqrt35`
c. `cos2 = 2cos2 – 1` (`costheta = sqrt35/6`)
`cos2theta = 17/18`
Question 3
Solve the equation `7cottheta = 3"cosec"theta` for `0^o < theta < 90^o`.
We have `cottheta = costheta/sintheta` and `"cosec"theta = 1/sintheta`
Subtitute it into the equation: `7costheta/sintheta = 3 1/sintheta → 7costheta = 3`
`costheta = 3/7 → theta = cos^-1(3/7) = 64.6^o`
Question 4
Solve the equation
`sec^2theta + tan^2theta = 5tantheta + 4` for `0^o< theta < 180^o`.
We have `sec^2theta = 1 + tan^2theta`
Substitute it into the equation:
`1 + tan^2theta + tan^2theta = 5tantheta + 4`
`2 tan^2theta - 5 tantheta - 3 = 0`
`tantheta = 3` or `tan theta = -1/2` → `theta= 71.6^o` and `theta=153.4^o`
Question 5
a. Show that `2"cosec"2thetacottheta -= "cosec"^2theta`.
b. Solve the equation `2 "cosec" phi cot frac{1}{2}phi + "cosec"1/2phi = 12` for `-360^o < phi < 360^o`. Show all necessary working.
a.
`"cosec"2theta = 1/(2sinθcosθ)`
Prove the LHS = RHS
`2"cosec"2thetacottheta = 2xx1/(2sinθcosθ) xx cosθ/sinθ = 1/sin^2theta = "cosec"2theta` (shown)
b.
`2"cosec" phi cot1/2phi + "cosec"1/2phi = 12`
`(2xx1/(2sin frac{1}{2}ϕcos frac{1}{2}phi) xx frac{cos frac{1}{2}phi}{sinfrac{1}{2}phi}) + "cosec"1/2 phi = 12`
`"cosec"^2 1/2phi +"cosec"1/2phi - 12 = 0`
`"cosec"1/2 phi = 3` or `"cosec"1/2 phi = -4`
Solve out we have the values of `phi` : `–331.0, –29.0, 38.9, 321.1` (degree)
Question 6
a.
i. Express `4sin theta + 4 cos theta` in the form `Rsin( theta+a )`, where `R > 0` and `0^o < alpha < 90^o`.
ii. Hence find the smallest positive value of `theta` satisfying the equation `4sintheta + 4costheta = 5`.
b. Solve the equation `4cot2x = 5 + tanx` for `0 < x < pi`, showing all necessary working and giving the answers correct to `2` decimal places.
a.
i. `4sin theta + 4 cos theta`
`Rsin(theta + a) = Rsin theta cos alpha+ Rcos thetasinalpha`
`Rcos alpha = 4` (1)
`Rsin alpha = 4` (2)
Now, to find `R`, square both equations and add them:
`R^2cos^2alpha + R^2sin^2alpha = 16 + 16 = 32`
Since `cos^2 alpha + sin^2alpha = 1`, `R^2 = 2` so `R = 4sqrt2`
Now, to find `alpha`, divide equation (2) by equation (1):
`tan alpha = frac{Rsinα}{Rcosα} = 1 → alpha = 45^o`
ii. `4sin theta + 4cos theta = 5`
`4sqrt2sin(theta + 45^o) = 5`
`theta+ 45^o = sin^-1((5)/(4sqrt2)) = 62.1^o`
`theta = 62.1^o - 45^o = 17.1^o` or `theta = 180^o - 62.1^o - 45^o = 72.9^o`
The smallest positive`17.1^o` value of `theta` is
b. `4cot2x = 5 + tanx` (`cot2x = 1/(tan2x)`)
`4/(tan2x) = 5 + tanx`
`4/(frac{2tanx}{1-tan^2x}) = 5 + tanx`
`2(1 – tan^2x) = (5 + tanx)tanx`
`2tan^2x + 5tanx - 2 = 0`
Solve out `x = 0.31` rad or `x = 2.03` rad
Question 7
a. Showing all necessary working, solve the equation `secalpha"cosec"alpha = 7` for `0^o < alpha < 90^o`.
b. Showing all necessary working, solve the equation `sin(beta + 20^o) + sin(beta - 20^o) = 6cosbeta` for `0^o < beta < 90^o`.
a. `secalpha"cosec"alpha = 7` (`sec alpha = 1/cos alpha`; `cscalpha = 1/sinalpha`)
`1/cosalpha xx 1/sin alpha = 7`
`sin2alpha = 2/7`
`2alpha = sin^-1(2/7) = 16.6^o`
`alpha= 16.6^o/2 = 8.3^o` or `alpha = frac(180^o-16.6^o)2 = 81.7^o`
b. `sin(beta + 20^o) + sin(beta - 20^o) = 6cosbeta`
We use the sum and difference identities for sine:
`sin(beta + 20^o) + sin(beta - 20^o) = 2sinbeta cos(20^o)`
`2sinbeta cos20^o = 6cosbeta`
Divide both sides for `cosbeta`
`tanbeta = 6/(2cos20^o) = 3.19`
Solve `beta= 72.6^o`
Question 8
a. Express `0.`theta`5costheta - 1.2sintheta` in the form `Rcos(theta+alpha )`, where `R > 0` and `0^o< alpha < 90^o`, giving the value of `alpha` correct to `2` decimal places.
b. Hence solve the equation `0.5costheta – 1.2sintheta = 0.8` for `0^o< theta < 360^o`.
c. Determine the greatest and least possible values of `(3 - costheta + 2.4sintheta)^2` as varies.
a. `0.5costheta – 1.2sintheta`
We express this in the form `Rcos(theta + alpha)`, where `R > 0` and `0^o < α < 90^o`.
The identity we use is:
`Rcos(theta + alpha) = Rcosthetacosalpha - Rsinthetasinalpha`
`Rcosalpha = 0.5` (1)
`Rsinalpha = 1.2` (2)
To find `R`, we square both equation and add them:
`R^2cos^2alpha + R^2sin^2alpha = 0.5^2 + 1.2^2`
`R^2 = 1.69`
`R = 1.3`
To find `alpha`, divide equation (2) by equation (1):
`tan alpha = 1.2/0.5= 2.4`
`alpha= 67.4`
b. `0.5costheta - 1.2sin theta = 0.8`
`0.5costheta - 1.2sintheta = 1.3cos(theta + 67.4)`
Solve `theta` with `2` values: `344.7` and `240.5`, respectively.
c. `(3 - costheta + 2.4sintheta )^2`
Combine `-costheta` and `2.4sintheta` into a single term using the same method as in part i.
We want to express it as `Rcos(theta+alpha)`, where:
`R = sqrt((-1)^2+2.4^2) = sqrt(1+5.76) = 2.6`
`tanalpha = 2.4/-1 = -2.4`
`alpha= tan^-1(-2.4) = -67.38^o`
Thus the expression becomes: `3 + 2.6cos(theta - 67.4^o)`
Max value `= 3 + 2.6(1) – 3 + 2.6 = 5.6`
Min value `= 3 + 2.6(–1) = 0.4`
The expression `(3 - costheta + 2.4sinθ)^2`
Max value `= (5.6)^2 = 31.36`
Min value `= (0.4)^2 = 0.16`
The greatest and least possible values are: `31.36` and `0.16`.
Question 9
Solve the equation `sec^2theta = 3 "cosec"theta` for `0^o< theta < 180^o`.
`sec^2theta = 3csctheta`
`sectheta = 1/cos theta` and `csc = 1/sintheta`
Substitute these into the equation:
`1/cos^2theta = 3/sintheta`
`sin theta = 3cos^2theta`
`sintheta = 3(1 - sin^2theta)`
`sin theta = 3 - 3sin^2theta`
`3sin^2theta + sintheta - 3 = 0`
`the= sin^-1(0.847) = 57.9`
`theta= 180 - 57.9 = 122.1`
Question 10
a. Use the factor theorem to show that `(2x +3)` is a factor of `8x^3 + 4x^2 - 10x + 3`.
b. Show that the equation `2cos2theta = frac{6costheta -5}{2costheta+1}` can be expressed as `8cos^3theta + 4cos^2theta - 10cos + 3 = 0`.
c. Solve the equation `2cos2theta = frac{6costheta -5}{2costheta+1}` for `0^o< theta < 360^o`.
a. `f(x) = 8x^3 + 4x^2 – 10x + 3`
To use the factor theorem, we substitute `x = -3/2` into `f(x)`:
`f(-3/2) = 8(-3/2)^2 + 4(-3/2)^2 - 10(-3/2) + 3 = 0`
Since `f(-3/2) = 0`, we have verified that `(2x + 3)` is a factor of the polynomial.
b. `2cos2theta = frac{6costheta -5}{2costheta+1}`
`8cos^3theta + 4cos^2theta - 10cos + 3 = 0`
c. `8cos^3theta + 4cos^2theta - 10cos + 3 = 0`
`(2x + 3)` is a factor of this cubic equaton. Let’s divide `8x^3 + 4x^2 - 10x + 3` by `2x + 3`
`(2x + 3)(4x^2 – 2x + 1) = 8x^3 + 4x^2 – 10x + 3` by `2x + 3`
`x = costheta = -3/2` (not valid)
`4x^2 – 4x + 1 = 0 → x = 0.5`
`x = cos theta = 0.5`
Solve `theta = 60` or `theta = 300`
Question 11
a. Given that `tan2thetacottheta = 8`, show that `tan^2theta = 3/4`.
b. Hence solve the equation `tan2thetacottheta = 8` for `0^o< theta < 180^o`.
a. `cot theta= 1/tantheta`
`tan2thetaxx1/tantheta = 8`; `tan2theta = (2tantheta)/(1 -tan^2theta)`
`frac{(2tantheta)/(1 -tan^2theta)}{tantheta} = 8 → (2)/(1 -tan^2theta)=8`
`1/4 = 1 – tan^2theta`
`tan^2theta = 3/4 → tantheta =+- sqrt3/2`
b. Solve out : `theta~~40.89^o` and `theta~~139.11^o`.
Question 12
a. Express `2costheta + (sqrt5)sintheta` in the form `Rcos( theta - alpha )` where `R > 0` and `0^o< theta < 90^o`, giving the value of `alpha` correct to `2` decimal places.
b. Hence solve the equation `2costheta + (sqrt5)sintheta =1` for `0^o.
a. `2costheta + (sqrt5)sintheta`
Use the formula `acostheta + bsintheta = Rcos(theta - α)` where `R = sqrt(a^2+ b^2)` and `tanalpha = a/b`.
b. Given `a = 2` and `b = sqrt5`
Calculate `R`: `R = sqrt(2^2+(5)^2) = 3`
Calculate `alpha`: `tan alpha = sqrt5/2alpha = tan^-1(sqrt5/2)~~ 48.19^o`
i. Solve `2costheta + (sqrt5)sintheta =1`
We already have from part i: `2costheta + (sqrt5)sintheta = 3cos(theta - alpha)`
`3cos(theta - alpha) = 1 → cos(theta - alpha) = 1/3`
`theta-alpha = cos^-1(1/3) + k360^o` or `theta- alpha=-cos^-1(1/3) + k360^o`
Solve out `theta= 118.72^o` or out `theta= 337.66^o`
Question 13
Solve the equation `5costheta(1 + cos2theta) = 4` for `0^o<= theta <= 360^o`.
`cos2theta = 2cos2theta - 1`
`5costheta(1 + 2cos^2theta - 1) = 4`
`10cos^3theta = 4`
`costheta = root(3)(4/10)`
`theta = cos^-1(root(3)(4/10)) + k360^o` or `theta= –cos^-1(root(3)(4/10)) + k360^o`
`theta= 42.5^o` or `theta = 317.5^o`
Question 14
Solve the equation `5tan2theta = 4cottheta` for `0^o.
`5tan2theta = 4cottheta`
`cottheta = 1/tan theta`; `tan2theta= (2tantheta)/(1-tan^2theta)`
We have: `5(2tantheta)/(1 -tan^2theta) = 4 1/tantheta`
Called `x = tantheta`
`5 (2x)/(1 - x^2) = 4 1/x → 10x^2 – 4 + 4x^2 = 0`
Solve quadratic equation, we have: `x =+- sqrt(2/7) → tantheta = +-sqrt(2/7)`
`theta= tan^-1(sqrt(2/7))` or `theta = tan^-1(-sqrt(2/7))`
Obtain `theta = 28.1` or `theta = 151.9`
Question 15
i.Show that `sin(theta + 60^o) + sin(theta + 120^o) -= sqrt3costheta`.
ii.Hence
a. Find the exact value of `sin105^o + sin165^o`.
b. Solve the equation `sin(theta + 60^o) + sin(theta + 120^o) = sectheta` for `0^o <= theta <= 180^o`.
i. `sin(theta + 60^o) + sin(theta + 120^o)-= sqrt3costheta`
We have the left side:
`sinthetacos60 + costhetasin60 + sinthetacos120 + costhetasin120` (1)
Therefore: `sin60 = sin120 = sqrt3/2` and `cos60 = 1/2`, `cos120 = -1/2`
Simplify (1), we have: `sintheta1/2 + costhetasqrt3/2 + sintheta(-1)/2 + costheta3/2 =sqrt3 costheta`
ii.
a. Find the exact value of `sin105^o + sin165^o`
`sin105^o + sin165^o= sin(45^o +60^o) + sin(45^o +120^o) = sqrt3cos45^o = sqrt6/2`
b. `sin(theta + 60^o) + sin(theta + 120^o) = sectheta` for `0^o <=theta<= 180^o`
`sqrt3costheta = sec theta = 1/costheta`
`costheta = +-1/sqrt3 = cos^-1(1/sqrt3)` or `theta= cos^-1(-1/sqrt3)`
`theta= 54.74` or `theta = -125.26`
Question 16
The polynomial `p(x)` is defined by
`p(x) = ax^3 + 3x^2 + bx + 12`,
where `a` and `b` are constants. It is given that `(x+3)` is a factor of `p(x)`. It is also given that the remainder is `18` when `p(x)` is divided by `(x+2)`.
a.Find the values of `a` and `b`
b. When `a` and `b` have these values,
Show that the equation `p(x) = 0` has exactly one real root.
c. Solve the equation `p(secy) = 0` for `-180^o< theta < 180^o`.
a. `p(x) = ax^3 + 3x^2 + bx + 12`
We have `(x + 3)` is a factor of `p(x)`. This means that `p(-3) = 0`.
The remainder is `18` when `p(x)` is divided by `(x +2)`. This means `p(-2) = 18`.
So `p(-3) = a(-3^3)+ 3(-3^2)+ b(-3) + 12 = 0`.
`27a + 3b = 39` (1)
`p(-2) = a(-2^3)+ 3(-2^2)+ b(-2) + 12 = 18`
`-8a - 2b = -6` (2)
From `2` equations, solve out: `a = 2` and `b = -5`
b.
i. `p(x) = 0` has exactly one real root
`p(x) = 2x^3 + 3x^2 -5x + 12`
Attempt division by `x + 3` at least as far as `2x^2 + kx`
Obtain quotient `2x^2 - 3x + 4`
Calculate discriminant of 3-term quadratic expression, or equivalent
Obtain `-23` and conclude appropriately
ii. `p(secy) = 0` for `-180 < theta < 180`
`p(secy) = 2(secy)^3 + 3(secy)^2 -5(secy) + 12 = 0`
`secy = 1/cosy` use this to solve equation
Solve `cosy = -1/3`
`y = 109.47` or `y = -109.47`
Question 17
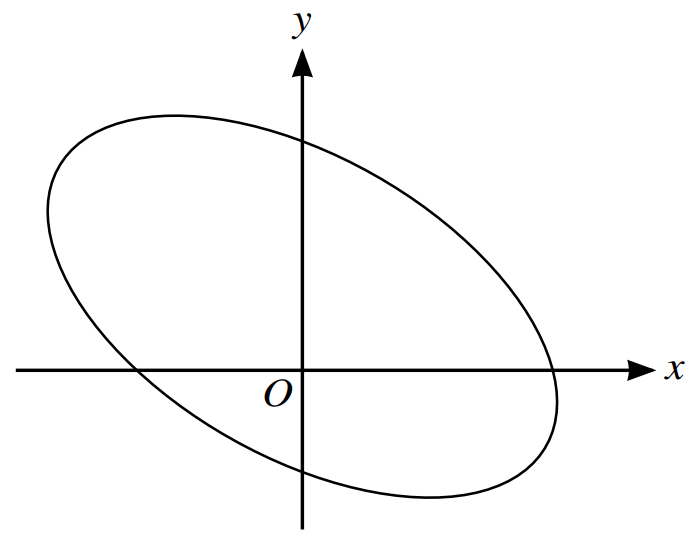
The diagram shows the curve with parametric equations `x = 4sintheta`,`y = 1 + 3cos(theta + pi/6)` for `0<= theta < 2pi`.
a. Show that `(dy)/(dx)` can be expressed in the form `k(1 + sqrt3tantheta)` where the exact value of k is to be determined.
b. Find the equation of the normal to the curve at the point where the curve crosses the positive y – axis. Give your answer in the form `y = mx + c`, where the constants `m` and `c` are exact.
`x = 4sintheta`,`y = 1 + 3cos(theta + pi/6)` for `0<= theta < 2pi`.
a. To find `(dy)/(dx)`, we need to compute `(dx)/(d theta)` and `(dy)/(d theta)` and use the chain rule: `(dy)/(dx)=frac{(dy)/(d theta)}{(dx)/(d theta)}`
`x = 4sintheta → (dx)/(d theta) = 4costheta`
`y = 1 + 3cos(theta + pi/6) → (dy)/(d theta) = -3sin(theta + pi/6) = -(3sqrt3)/(2)sintheta - 3/2costheta`
`(dy)/(dx) = frac{-(3sqrt3)/(2)sintheta-3/2costheta}{4costheta}`
Simplify: `(dy)/(dx) = -3/8(1+ sqrt3tantheta)`, so `k = -3/8`
b. Find the corresponding y–coordinate when `theta= 0`
`y = 1 + 3cos(0 + pi/6) = 1 + 3cos frac(pi)(6)`
So figure out `(0, 1 + (3sqrt3)/(2))`
Find the slope of the tangent line at `theta= 0`
`(dy)/(dx) = -3/8(1+ sqrt3tan0) = -3/8`
Find the slope of the normal line: `m = frac{-1}{(-3)/(8)} = 8/3`
The equation of the normal line: point `(0, 1 + (3sqrt3)/(2))` and slope `m = 8/3`
So the equation of the normal line: `y = 8/3x + 1 + (3sqrt3)/(2)`
Question 18
a. Express `sin2theta(3sectheta + 4"cosec" θ)` in the form `asin theta + bcostheta`, where `a` and `b` integers.
b. Hence express `sin2theta(3sectheta + 4"cosec" θ)` in the form `Rsin(theta + alpha)` where `R > 0` and `0^o< theta < 90^o`.
c. Using the result of part (ii), solve the equation `sin2theta(3sectheta + 4"cosec" θ) = 7` for `0^o <= theta <= 360^o`.
a. `sin2theta(3sectheta + 4"cosec" θ)`
`= sin2theta(3. 1/costheta + 4. 1/sintheta)`, therefore `sin2theta = 2sinthetacostheta`
`= 2sinthetacostheta (3. 1/costheta + 4. 1/sintheta)`
`= 6sintheta + 8costheta`
The expression in the form `asintheta + bcostheta` is: `6sintheta + 8costheta`
`a = 6` and `b = 8`.
b. Express `sin2theta(3sectheta + 4"cosec" θ)` in the form `Rsin( theta+ alpha)`
`R = sqrt(a^2+ b^2)` and `tan alpha = a/b`.
So `R = sqrt(6^2+ 8^2) = 10`
`tanalpha = 8/6 = 4/3 → alpha = 53.1`
c. `sin2theta(3sectheta + 4"cosec" θ) = 7`
`10sin(theta + alpha) = 7/10` with `alpha= 53.1`
`theta= 82.4` and `theta= 351.3`
Question 19
It is given that `theta` is an acute angle measured in degrees such that
`2sec^2theta + 3tantheta = 22`
a.Find the value of `tantheta`,
b. Use an appropriate formula to find the exact value of `tan(theta + 135^o)`.
`2sec^2thet`tan theta = 5/2`a + 3tantheta = 22` (`sec^2 theta = 1 + tan^2theta`)
a. `2(1 + tan^2theta) + 3tantheta = 22`
Solve out
b. `tan(theta + 135^o)`
Use the formula for the tangent: `tan(A+B) = frac{tanA +tanB}{1 -tanAtanB}`
`tan(theta + 135^o) = frac{tantheta +tan135}{1 -tanthetatan135} = frac{5/2 +tan135}{1 - 5/2tan135} = 3/7`
Question 20
a. Express `8sintheta 15costheta` in the form `Rsin(theta + alpha)`, where `R > 0` and `0^o< alpha < 90^o`. Given that value of `alpha` correct to `2` decimal places.
b. Hence solve the equation `8sintheta + 15costheta = 6` for `0^o <= theta <= 360^o`.
a. `8sintheta + 15costheta` in the form `Rsin(theta + alpha)`, where `R > 0` and `0^o< alpha < 90^o`.
`Rsin(theta + alpha) = R(sinthetacosalpha + costhetasinalpha)`
We need to math this to `8sintheta + 15costheta`
`Rcos alpha= 8` and `Rsin alpha = 15`
`R = sqrt(8^2+15^2) = 17`
Following that `tan alpha = 15/8`, solve out `alpha= 61.93`
The expression is `8sintheta + 15costheta = 17sin(theta + 61.93)`
b. `8sintheta + 15costheta=6`
`17sin(theta + 61.93)=6`
Solve `theta= 97.4` or `theta = 318.7`
Question 1

The diagram shows part of the curve with equation `y = x^3cos2x`. The curve has a maximum at the point `M`.
a. Show that the x-coordinate of M satisfies the equation `x = root(3)(1.5x^2cot2x)`.
b. Use the equation in part (a) to show by calculation that the x-coordinate of `M` lies between `0.59` and `0.6`.
c. Use an iterative formula, based on the equation in part (a), to find the x-coordinate of `M` correct to `3` s.f. Given the result of each iteration to `5` s.f.
Question 2
It is given that `3sin2theta= costheta` where `θ` is an angle such that `0^o< theta < 90^o`.
a. Find the exact value of `sintheta`.
b. Find the exact value of `sectheta`.
c. Find the exact value of `cos2theta`.
Question 3
Solve the equation `7cottheta = 3"cosec"theta` for `0^o < theta < 90^o`.
Question 4
Solve the equation
`sec^2theta + tan^2theta = 5tantheta + 4` for `0^o< theta < 180^o`.
Question 5
a. Show that `2"cosec"2thetacottheta -= "cosec"^2theta`.
b. Solve the equation `2 "cosec" phi cot frac{1}{2}phi + "cosec"1/2phi = 12` for `-360^o < phi < 360^o`. Show all necessary working.
Question 6
a.
i. Express `4sin theta + 4 cos theta` in the form `Rsin( theta+a )`, where `R > 0` and `0^o < alpha < 90^o`.
ii. Hence find the smallest positive value of `theta` satisfying the equation `4sintheta + 4costheta = 5`.
b. Solve the equation `4cot2x = 5 + tanx` for `0 < x < pi`, showing all necessary working and giving the answers correct to `2` decimal places.
Question 7
a. Showing all necessary working, solve the equation `secalpha"cosec"alpha = 7` for `0^o < alpha < 90^o`.
b. Showing all necessary working, solve the equation `sin(beta + 20^o) + sin(beta - 20^o) = 6cosbeta` for `0^o < beta < 90^o`.
Question 8
a. Express `0.`theta`5costheta - 1.2sintheta` in the form `Rcos(theta+alpha )`, where `R > 0` and `0^o< alpha < 90^o`, giving the value of `alpha` correct to `2` decimal places.
b. Hence solve the equation `0.5costheta – 1.2sintheta = 0.8` for `0^o< theta < 360^o`.
c. Determine the greatest and least possible values of `(3 - costheta + 2.4sintheta)^2` as varies.
Question 9
Solve the equation `sec^2theta = 3 "cosec"theta` for `0^o< theta < 180^o`.
Question 10
a. Use the factor theorem to show that `(2x +3)` is a factor of `8x^3 + 4x^2 - 10x + 3`.
b. Show that the equation `2cos2theta = frac{6costheta -5}{2costheta+1}` can be expressed as `8cos^3theta + 4cos^2theta - 10cos + 3 = 0`.
c. Solve the equation `2cos2theta = frac{6costheta -5}{2costheta+1}` for `0^o< theta < 360^o`.
Question 11
a. Given that `tan2thetacottheta = 8`, show that `tan^2theta = 3/4`.
b. Hence solve the equation `tan2thetacottheta = 8` for `0^o< theta < 180^o`.
Question 12
a. Express `2costheta + (sqrt5)sintheta` in the form `Rcos( theta - alpha )` where `R > 0` and `0^o< theta < 90^o`, giving the value of `alpha` correct to `2` decimal places.
b. Hence solve the equation `2costheta + (sqrt5)sintheta =1` for `0^o.
Question 13
Solve the equation `5costheta(1 + cos2theta) = 4` for `0^o<= theta <= 360^o`.
Question 14
Solve the equation `5tan2theta = 4cottheta` for `0^o.
Question 15
i.Show that `sin(theta + 60^o) + sin(theta + 120^o) -= sqrt3costheta`.
ii.Hence
a. Find the exact value of `sin105^o + sin165^o`.
b. Solve the equation `sin(theta + 60^o) + sin(theta + 120^o) = sectheta` for `0^o <= theta <= 180^o`.
Question 16
The polynomial `p(x)` is defined by
`p(x) = ax^3 + 3x^2 + bx + 12`,
where `a` and `b` are constants. It is given that `(x+3)` is a factor of `p(x)`. It is also given that the remainder is `18` when `p(x)` is divided by `(x+2)`.
a.Find the values of `a` and `b`
b. When `a` and `b` have these values,
Show that the equation `p(x) = 0` has exactly one real root.
c. Solve the equation `p(secy) = 0` for `-180^o< theta < 180^o`.
Question 17
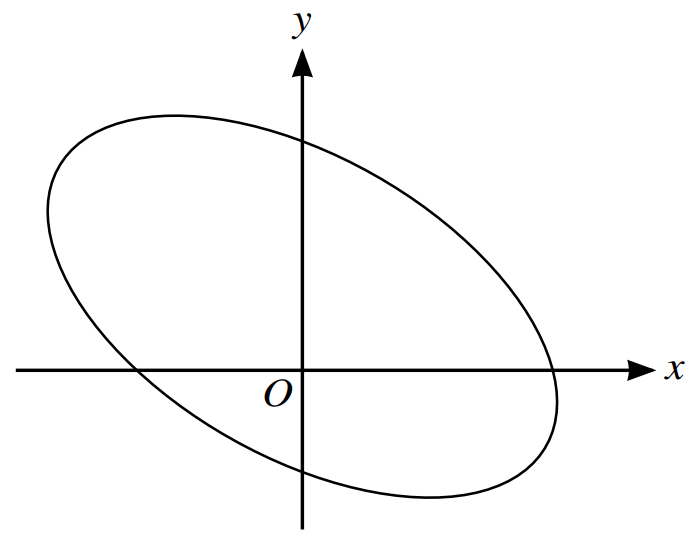
The diagram shows the curve with parametric equations `x = 4sintheta`,`y = 1 + 3cos(theta + pi/6)` for `0<= theta < 2pi`.
a. Show that `(dy)/(dx)` can be expressed in the form `k(1 + sqrt3tantheta)` where the exact value of k is to be determined.
b. Find the equation of the normal to the curve at the point where the curve crosses the positive y – axis. Give your answer in the form `y = mx + c`, where the constants `m` and `c` are exact.
Question 18
a. Express `sin2theta(3sectheta + 4"cosec" θ)` in the form `asin theta + bcostheta`, where `a` and `b` integers.
b. Hence express `sin2theta(3sectheta + 4"cosec" θ)` in the form `Rsin(theta + alpha)` where `R > 0` and `0^o< theta < 90^o`.
c. Using the result of part (ii), solve the equation `sin2theta(3sectheta + 4"cosec" θ) = 7` for `0^o <= theta <= 360^o`.
Question 19
It is given that `theta` is an acute angle measured in degrees such that
`2sec^2theta + 3tantheta = 22`
a.Find the value of `tantheta`,
b. Use an appropriate formula to find the exact value of `tan(theta + 135^o)`.
Question 20
a. Express `8sintheta 15costheta` in the form `Rsin(theta + alpha)`, where `R > 0` and `0^o< alpha < 90^o`. Given that value of `alpha` correct to `2` decimal places.
b. Hence solve the equation `8sintheta + 15costheta = 6` for `0^o <= theta <= 360^o`.