Question 1
A curve hass parametric equations `x = e^t – 2e^-t, y = 3e^(2t) +1`
find the equation of the tangent to the curve at the point for which `t = 0`. [5]
Medium
Mark as Complete
Mark Scheme
Question 2
Find the exact coordinates of the stationary point on the curve with equation `y=5xe^(1/2x)` [5]
Easy
Mark as Complete
Mark Scheme
Question 3
The equation of a curve is `cos3x + 5siny = 3`
Find the gradient of the curve at the point `(pi/9, pi/6)` [5]
Medium
Mark as Complete
Mark Scheme
Question 4
A curve is defined by the parametric equations : `x = 3t - 2sint`, `y = 5t + 4cost`
Where `0<= t <=2π`. At each of the points P and Q on the curve, the gradient of the curve is `5/2`.
a.Show that the values of t at P and Q satisfy the equation `10cost – 8sint = 5` [3]
b.Express `10cost – 8sint` in the form Rcos`(t +alpha )`, where `R > 0` and `0 . Give the exact value of R and the value of `alpha` correct to `3`s.f.[4]
c.Hence find the values of t at the points P and Q. [4]
Medium
Mark as Complete
Mark Scheme
Question 5
The equation of a curve is `2e^(2x)y – y^3 + 4 = 0.`
a.Show that `(dy)/dx = frac{4ye^(2x)}{3y^2 -2e^(2x)}`. [4]
b.The curve passes through the point `(0,2)`.
Find the equaion of the tangent to the cruve ar this point, giving your answer in the for, `ax + by + c = 0`. [3]
Show that the curve has no stationary points [2]
Hard
Mark as Complete
Mark Scheme
Question 6
Find the equation of the normal to the curve `x^2lny + 2x + 5y = 11` at the point `(3,1)`.
Medium
Mark as Complete
Mark Scheme
Question 7
Find the exact coordinates of the stationary point of the curve with equation `y = (3x)/lnx`.
Easy
Mark as Complete
Mark Scheme
Question 8
A curve has equation `y = frac{3+ 2lnx}{ 1 + lnx}`. Find the exact gradient of the curve at the point for which`y = 4`.
Easy
Mark as Complete
Mark Scheme
Question 9
The equation of a curve is `x^2 – 4xy – 2y^2 = 1`.
a.Find an expression for `(dx)/dy` and show that the gradient of the curve at the point `(-1, 2)` is `-5/2`.
b.Show that the curve has no stationary points.
c.Find the x-coordinate of each of the points on the curve at which the tangent is parallel to the y – axis.
Medium
Mark as Complete
Mark Scheme
Question 10
The parametric equations of a curve are
`x =3sin2theta, y = 1 + 2tan2θ`, for `0<=theta<= pi/4`.
Find the exact gradient of the curve at the point for which `theta= pi/6`.
Find the value of `theta` at the point where the gradient of the curve is `2`, giving the value correct to `3` s.f.
Easy
Mark as Complete
Mark Scheme
Question 11
A curve has equation `y = 4xsin frac{1}{2} x`. Find the equation of the tangent to the curve at the point for which `x = pi`.
Easy
Mark as Complete
Mark Scheme
Question 12
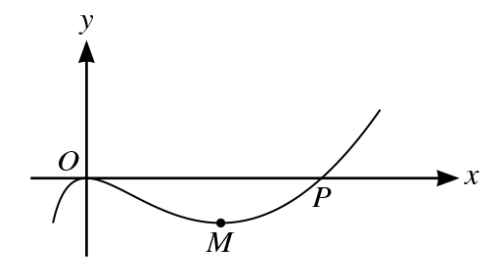
The diagram shows part of the curve defined by the parametric equations
`x = t^2 + 4t, y = t^3 – 3t^2`
The curve has a minimum point at `M` and crosses the x-axis ar the point P.
a. Find the gradient of the curve at P.
b. Find the coordinates of the point M.
c.The value of the gradient of the curve at the point with parameter t is denoted by m. Show that `3t^2 – (2m + 6)t – 4m = 0` and hence find the set of possible values of `m` for points on the curve.
Hard
Mark as Complete
Mark Scheme
Question 13
A curve has equation `y = 3ln(2x + 9) -2lnx`.
a. Find the x-coordinates of the stationary point.
b. Determine whether the stationary point is a maximum or minimum point.
Medium
Mark as Complete
Mark Scheme
Question 14
A curve has parametric equations
`x = t + ln(t +1), y = 3te^(2t)`
a. Find the equation of the tangent to the curve at the origin.
b. Find the coordinates of the stationary point, giving each coordinate correct to `2` decimal places.
Medium
Mark as Complete
Mark Scheme
Question 15
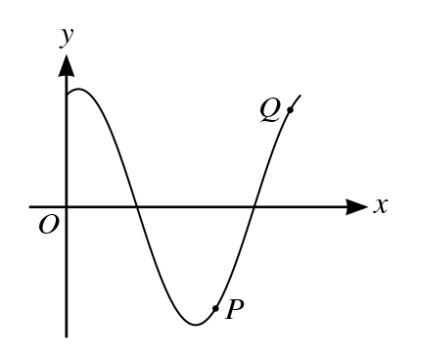
The diagram shows the curve with equation `y = sin2x + 3cos2x` for `0 ≤x≤ pi`. At the points P and Q on the curve, the gradient of the curve is `3`.
a. Find an expression for `(dy)/dx`.
b. By first expressing `(dy)/dx` in the form `Rcos(2x + alpha )`, where `R > 0` and `0≤x≤pi/2`, find the x- coordinates of P and Q, giving your answers correct to `4` s.f.
Medium
Mark as Complete
Mark Scheme
Question 16
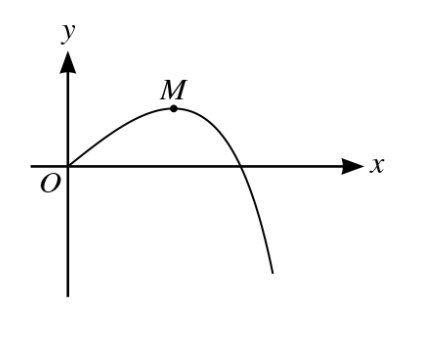
The diagram shows the curve with equation `y = 5sin2x – 3tan2x` for values of x such that`0≤x≤pi/4`. Find the x-coordinates of the stationary point M, giving your answer correct to `3`s.f.
Easy
Mark as Complete
Mark Scheme
Question 17
The parametric equations of a curve are
`x = t^3 = 6t + 1, y = t^4 – 2t^3 + 4t^2 – 12t + 5`
a.Find `(dy)/dx` and use division to show that `(dy)/dx` can be written in the form `at + b`, where a and b are constants to be found.
b.The straight line `x -2y +9 = 0`is the normal to the curve at point P. Find the coordinates of P.
Medium
Mark as Complete
Mark Scheme
Question 18
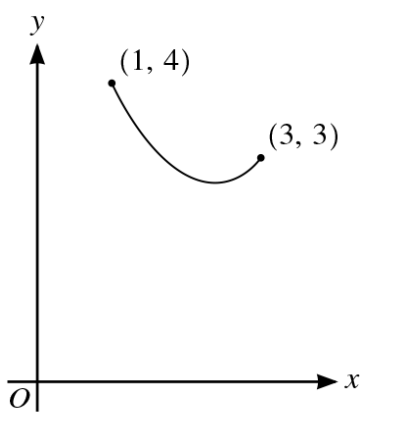
The diagram shows the curve with parametric equations
`x = 2 - cos2t`, `y = 2sin^3t + 3cos^3t + 1` for `0≤x≤pi/2`. The endpoints of the curve are `(1,4)` and `(3,3)`.
a.Show that `(dy)/dx` `= 3/2sint - 9/4cost`
b.Find the coordinates of the minimum point, giving each coordinate correct `3` s.f.
c.Find the exact gradient of the normal to the curve at the point for which `x =2`
Medium
Mark as Complete
Mark Scheme
Question 19
The equation of a curve is `x^2 + 4xy + 2y^2 = 7`.
a. Find the equation of the tangent to the curve at the point`(-1,3)`. Give your answer in the form `ax + by + c = 0` where `a`, `b` and `c` are integers.
b. Show that there is no point on the curve at which the gradient is `1/2`.
Medium
Mark as Complete
Mark Scheme
Question 20
The diagram shows the part of the curve `y = 3e^-xsin2x` for `0≤x≤pi/2`, and the stationary point M.
a. Find the equation of the tangent to the curve at the origin.
b. Find the coordinates of M, giving each coordinate correct to `3` decimal places.
Easy
Mark as Complete
Mark Scheme
Question 1
A curve hass parametric equations `x = e^t – 2e^-t, y = 3e^(2t) +1`
find the equation of the tangent to the curve at the point for which `t = 0`. [5]
Find the coordinates of the point where `t = 0`.
The parametric equations are:
`x(0)= e^0 – 2e^0 = 1 – 2 = -1`
`y(0) = 3e^(2 xx 0) +1 = 3(1) + 1 = 4`
So, the point on the curve at`t = 0` is `(-1, 4)`.
Find the derivatives `(dx)/dt` and `(dy)/dt` at `t = 0`.
`(dx)/dt = e^t + 2^(e-t)`, with `t = 0`, we have: `(dx)/dt = 1 + 2 = 3`
`(dy)/dt = 6e^(2t)`, with `t = 0`, we have: `(dy)/dt = 6`
Find the slope of the tangent line
`(dy)/dx = frac{(dy)/dt}{ (dx)/dt} = 6/3 = 2`
Write the equation of the tangent line
`y – y_1 = m(x – x_1)`
`y – 4 = 2(x +1)`
`y = 2x +6`
Question 2
Find the exact coordinates of the stationary point on the curve with equation `y=5xe^(1/2x)` [5]
Find the derivative `(dy)/dx`
Use`u = 5x-> u’ = 5`
`v = e^(1/2x)-> v’ = 1/2e^(1/2x)`
`(dy)/dx = u’v + v’u = 5e^(1/2x) + 5/2xe^(1/2x)`
Set the derivative equal to zero
`(dy)/dx = 0`
`5e^(1/2x) + 5/2xe^(1/2x) = 0-> 5e^(1/2x)( 1/2x +1) = 0`
`5e^(1/2x) = 0`can't approach zero
`1/2x +1 = 0-> x = -2-> y = -10e^-1`
Question 3
The equation of a curve is `cos3x + 5siny = 3`
Find the gradient of the curve at the point `(pi/9, pi/6)` [5]
Find the derivative `(dy)/dx`
`d/dx[ cos3x + 5siny]`(Differentiate the given equation with respect to x)
`d/dx[ cos3x] + d/dx[5siny] = 0`
`d/dx[5siny] = 5cosyxx (dy)/dx`
`-3sin3x + 5cosyxx (dy)/dx = 0`
`5cosyxx(dy)/dx = 3sin3x`
`(dy)/dx =frac{ 3sin3x}{ 5cosy}`
Substitute the given point: `(dy)/dx =frac{ 3sin3pi/9}{ 5cos frac{pi}{6}} = 3/5.`
The gradient of the curve at the point`(pi/9, pi/ 6)` is `3/5`
Question 4
A curve is defined by the parametric equations : `x = 3t - 2sint`, `y = 5t + 4cost`
Where `0<= t <=2π`. At each of the points P and Q on the curve, the gradient of the curve is `5/2`.
a.Show that the values of t at P and Q satisfy the equation `10cost – 8sint = 5` [3]
b.Express `10cost – 8sint` in the form Rcos`(t +alpha )`, where `R > 0` and `0 . Give the exact value of R and the value of `alpha` correct to `3`s.f.[4]
c.Hence find the values of t at the points P and Q. [4]
a.`(dy)/dx =frac{(dy)/dt}{(dx)/dt`
Given the parametric equations:
`x = 3t - 2sint`and `y = 5t + 4cost`
We first calculate `(dx)/dt` and `(dy)/dt`
`(dx)/dt = d/dt(3t - 2sint) = 3 – 2 sint`
`(dy)/dt = d/dt(5t + 4cost) = 5 – 4sint`
So the gradient `(dy)/dx = frac{5 - 4 sint}{ 3 - 2 cost}`
We are given that at point P and Q, the gradie`(t +alpha )`nt is `5/2`.
`frac{5 - 4 sint}{ 3 - 2 cost} = 5/2`
Cross-multiplying we have: `10cost – 8sint = 5`
b.To express`10cost – 8sint`in the form Rcos(t + ), use the identity:
Rcos`(t +alpha )` = `Rcostcosalpha` - `Rsintsinalpha` , so we got:
R`cos alpha= 10` and R`sinalpha = 8`
To find R, square and add both equations:
`R^2 = (Rcosalpha )^2 + (Rsinalpha )^2 = 10^2 + 8^2 = 164`
`R = 2sqrt41`
`tanalpa = frac{Rsinalpha }{Rcosalpha }= 8/10 = 0.8`
`alpha= 0.674` radians
`10cost – 8sint = 2sqrt41cos( t + 0.674)`
c.Find the values of t at the points P and Q
We are given the equation `2sqrt41cos(t + 0.674) = 5`
Find out `cos(t + 0.674) = 5/(2sqrt41)~~ 0.39`
`t + 0.674 = 1.164` or`t + 0.674 = 2pi – 1.168`
`t = 0.494` or`t = 4.44`
Question 5
The equation of a curve is `2e^(2x)y – y^3 + 4 = 0.`
a.Show that `(dy)/dx = frac{4ye^(2x)}{3y^2 -2e^(2x)}`. [4]
b.The curve passes through the point `(0,2)`.
Find the equaion of the tangent to the cruve ar this point, giving your answer in the for, `ax + by + c = 0`. [3]
Show that the curve has no stationary points [2]
a.`2e^(2x)y – y^3 + 4 = 0.`
To find `(dy)/dx`, we implicitly differentiate the equation with respect to x
Differentiate `2e^(2x)y` with respect to x
`d/dx(2e^(2x)y) = 4e^(2x)y + 2e^(2x) (dy)/dx`
Differentiate `-y^3` with respect to x:
`d/(dx)(-y^3) = -3y^(2(dy)/dx)`
Subtitute these derivatives back into the original equation:
`4e^(2x)y + 2e^(2x )(dy)/dx- 3y^(2(dy)/dx) = 0`
`(dy)/dx(2e^(2x) – 3y^2) = -4e^(2x)y`
`(dy)/dx = frac{4ye^(2x)}{3y^2 -2e^(2x) }`
The curve passes through the point`(0,2)`
To find the equation of the tangent, first compute the derivative dydx at the point `(0,2)`.
Substitute `x = 0` and`y =2` into the expression for `(dy)/dx`:
`(dy)/dx =frac{ 4ye^(2x)}{3y^2 -2e^(2x)} = 0.8`
Use the point-slope form to find the equation of the tangent:
`y - 2 = 0.8(x - 0)-> y = 0.8x + 2`
Express in the form `ax + by + c = 0`
`8x – 10y + 20 = 0`
c.Equate the numerator of the derivative to zero:
`4ye^(2xy) = 0`
Since `e^(2xy)ne 0`, y must be `0` for `(dy)/dx = 0`
Check if `y = 0` satisfies the orginal curve equation. Substitue `y = 0` into the original curve equation:
`2e^0 – 0^3 + 4 = 6 ne 0`
Therefore, `y = 0` does not satisfy the equation, hence there are no stationary points.
Question 6
Find the equation of the normal to the curve `x^2lny + 2x + 5y = 11` at the point `(3,1)`.
`x^2lny + 2x + 5y = 11`
Differentiate both sides with respect to `x`:
`d/dx(x^2lny) + d/dx(2x) + d/dx(5y) = d/dx(11)`
`2xlny+ (x^2)/y-(dy)/dx + 2 + 5(dy)/dx = 0`
Substitute the point `(3,1)` into the derivative equation.
Substitute `x = 3` and `y = 1` into the equation:
`2(3)ln(1) + 3^2/1(dy)/dx + 2 + 5(dy)/dx = 0`
So `(dy)/dx = -1/7`
This is the slope of the tangent line at the point `(3,1)`.
The slope of the normal is the negative reciprocal of the slope of the tangent line:
Slope of the normal `= -1/frac{-1}{7} = 7`
The equation of a line in point-slope form is
`y – y_1 = m(x – x_1)` (with point`(3,1)` and `m = 7`)
So the equation we get : `y = 7x -20`
Question 7
Find the exact coordinates of the stationary point of the curve with equation `y = (3x)/lnx`.
Given `y = (3x)/lnx`
To find the stationary points, we need to find the derivative `(dy)/dx` and set it equal to zero.
`(dy)/dx =frac{ (lnx)xxd/dx(3x) -3x xxd/dx(lnx)} {(lnx)^2} =frac{ (lnx)(3)-3x(1/x)}{(lnx)^2}`
Take `(dy)/dx = 0-> frac{(lnx)(3)-3x(1/x)}{(lnx)^2} = 0`
`3lnx – 3 = 0 → lnx = 1`
Find out `x = e`, therefore substitute it back into the original equation to find the y-coordinate: `y = 3e`
So the exact coordinates of the stationary point are: `(e,3e)`
Question 8
A curve has equation `y = frac{3+ 2lnx}{ 1 + lnx}`. Find the exact gradient of the curve at the point for which`y = 4`.
Differentiate the function with respect to `x`
`y = frac{3+ 2lnx}{ 1 + ln}`
`d/dx(frac{ 3+ 2lnx}{ 1 + lnx}) = frac{(3+2lnx)'(1+lnx) -(1+lnx)'(3+2lnx)}{ (1+lnx)^2} = frac{-1}{x(1+lnx)^2}`
Find the value of x when `y = 4`
`4 = frac{3+ 2lnx}{ 1 + lnx}->` Solve out `x = 1/sqrte`
Substitute`x = 1/sqrte` into the expression for `(dy)/dx = frac{-1}{x(1+lnx)^2}`
So `(dy)/dx =frac{ -1}{1/sqrtexx1/4} = -4sqrte` (the gradient of the curve where `y = 4`)
Question 9
The equation of a curve is `x^2 – 4xy – 2y^2 = 1`.
a.Find an expression for `(dx)/dy` and show that the gradient of the curve at the point `(-1, 2)` is `-5/2`.
b.Show that the curve has no stationary points.
c.Find the x-coordinate of each of the points on the curve at which the tangent is parallel to the y – axis.
a.`x^2 – 4xy – 2y^2 = 1`.
Diffrentiate each term with respect tp u. treating x as a function of y:
`d/dy(x^2) - d/dy(4xy) -d/dy(2y^2) = d/dy(1)`
`2x(dx)/dy – 4(x + yxx (dx)/dy ) – 4y = 0`
Simplify: `(dx)/dy = frac{2x -4y}{4x+4y}`
Substitute the point `(–1,2)`into `(dx)/dy`, so the calculated value is `-5/2`
b.To show that the curve has no stationary points, equate numerator of derivative to zero: `2x − 4y = 0-> x = 2y`
Substitute`y = −1`into the original curve equation:
`(2y)^2 −4(2y)y −2y^2 = 1 ->−6y^2 = 1`
So the curve has no stationary points.
c.To find the x-coordinate of each of the points on the curve at which the tangent is parallel to the y – axis, use denominator of derivative equated to zero: `4x + 4y = 0 -> y = –x`
`x^2 – 4x(-x) – 2(x) ^2 = 1`.
`3x^2 = 1-> x =+- 1/sqrt3`
Question 10
The parametric equations of a curve are
`x =3sin2theta, y = 1 + 2tan2θ`, for `0<=theta<= pi/4`.
Find the exact gradient of the curve at the point for which `theta= pi/6`.
Find the value of `theta` at the point where the gradient of the curve is `2`, giving the value correct to `3` s.f.
Find `(dx)/(dθ)` and `(dy)/(dθ)`
`(dx)/(dθ) = 3xxd/(dθ)(sin2θ) = 3xx2cos2theta = 6cos2theta`
`(dy)/(dθ) = 2xxd/(dθ)(tan2θ) = 2xx2sec^(2)2theta = 4sec^(2)2theta`
Find the gradient `(dy)/dx`
`(dy)/dx = frac{(dy)/(d theta)}{(dx)/(d theta)} = frac{4sec^(2)2θ}{6cos2θ} =frac{ 2sec^(2)2θ}{3cos2θ} = frac{2}{3cos^(3)2θ}`
Substitute `theta = pi/6` into `(dy)/dx`. So `(dy)/dx = 16/3`
`(dy)/dx =frac{ 2}{3cos^(3)2θ} = 2`
`cos2θ = (1/4)^(1/3)~~ 0.693 ->theta =( 0.808)/2 ~~ 0.404` radians
Question 11
A curve has equation `y = 4xsin frac{1}{2} x`. Find the equation of the tangent to the curve at the point for which `x = pi`.
Differentiate the curve equation to find the slope of the tangent
`(dy)/dx = (4x)'sinfrac{1}{2}x + sin(1/2x)'4x`
`= 4sinfrac{1}{2}x + 4x1/2cos12x = 4sinfrac{1}{2}x + 2xcosfrac{1}{2}x`
Substitute `x = pi` into `(dy)/dx-> 4sinfrac{1}{2}pi + 2pi cosfrac{1}{2}pi = 4`
So the gradient of the slope is `4`.
Find the coordinates of the point on the curve at `x = pi`
Substitute `x = pi` into the original equation to find `y`:
`y = 4pi sin(1/2pi) = 4pi xx 1 = 4pi`
So the point on the curve at `x = pi` is `(π, 4 π)`
The equation of the tangent line: `y - y_1 = m(x - x_1)`
Where `(x_1, y_1)``= (π, 4 π)` and `m = 4`
So the final the equation is `y = 4x`
Question 12

The diagram shows part of the curve defined by the parametric equations
`x = t^2 + 4t, y = t^3 – 3t^2`
The curve has a minimum point at `M` and crosses the x-axis ar the point P.
a. Find the gradient of the curve at P.
b. Find the coordinates of the point M.
c.The value of the gradient of the curve at the point with parameter t is denoted by m. Show that `3t^2 – (2m + 6)t – 4m = 0` and hence find the set of possible values of `m` for points on the curve.
a.Differentiate `x(t)` and `y(t)`
Given `x(t) = t^2 + 4t`
`y(t) = t^3 – 3t^2`
Differentiate `x(t)` with respect to `t`: `(dx)/dt = 2t + 4`
Differentiate `y(t)` with respect to `t`: `(dy)/dt = frac{3t^2-6t}{2t+4 }`
Calculate the gradient `(dy)/dx =frac{(dy)/dt}{(dx)/dt} =frac{ 3t^2-6t}{2t+4}`
Find the gradient at point P where `t = 3`
Substitute `t = 3` into the gradient expression: `frac{3t^2-6t}{2t+4} =frac{ 3 x 9^2-6 x 9}{2 x 9 +4} = 9/10`
b.Find the coordinates of the point M (minimum point)
Let `(dy)/dx = 0-> 3t^2-6t = 0-> t = 0` and `t = 2`
Find the coordinates of M by substitute `t = 2` into `x(t)` and `y(t)`
`x_M = 12` and `y_M = -4`
c.`3t^2 – (2m + 6)t – 4m = 0`
`m = frac{3t^2-6t}{2t+4}`
`3t^2 – (2m + 6)t – 4m = 0`
The discriminant must be non-negative: `(2m + 6)^2 + 48m >= 0`
Solve the problem, we have : `m<= -sqrt72 – 9m`, `m >=sqrt72 – 9m`
Question 13
A curve has equation `y = 3ln(2x + 9) -2lnx`.
a. Find the x-coordinates of the stationary point.
b. Determine whether the stationary point is a maximum or minimum point.
a.Differentiate y with respect to x: `y = 3ln(2x + 9) - 2lnx`.
`(dy)/dx = [3ln(2x + 9)]' - (2lnx)' = 3/2xxfrac{1}{2x+9} - 2/x`
Set the derivative equal to zero to find the stationary points
`frac{6}{2x+9} - 2/x = 0-> 6x - 2(2x+9) = 0`
Solve out `x = 9`
b.To find the stationary point is a maximum or minimum point, we use the second derivative test.
We need to differentiate `(dy)/dx` to find the second derivative `(d^2y)/(d^2x)`
`frac{d^2y}{d^2x }= frac{-24}{(2x+9)^2} + 2/(x^2)`
Substitute `x = 9` into the second derivative to check the concavity:
Since `(d^2y)/(d^2x)` is negative, the stationary point at `x = 9` is a maximum point, as correctly concluded in the original solution.
Question 14
A curve has parametric equations
`x = t + ln(t +1), y = 3te^(2t)`
a. Find the equation of the tangent to the curve at the origin.
b. Find the coordinates of the stationary point, giving each coordinate correct to `2` decimal places.
a.To find the equation of the tangent, we need to determine the slope of the curve at the point where `t = 0`. We find the derivatives `(dx)/dt` and `(dy)/dt` and then using them to find the slope `(dy)/dx` at `t = 0`.
Find `(dx)/dt` :
`(dx)/dt= d/dt(t + ln(t + 1)) = 1 + 1/(t+1)`
At`t = 0`: `(dx)/dt = 1 + 1/1 = 2`
Find `(dy)/dt`:
`(dy)/dt = d/dt(3te^(2t)) = 3e^(2t) + 6te^(2t)`
At `t = 0`: `(dx)/dt = 3e^0 + 6(0)e^0 = 3`
Find the slope
`(dy)/dx = frac{(dy)/dt}{(dx)/dt} = 3/2`
Since the tangent passes through the origin `(0,0)`, the equation of the tangent is:`y = 3/2x`
b. A stationary point occurs when `(dy)/dt = 0`. From part (a), we know that:
`(dy)/dt = 3e^(2t) + 6te^(2t)`
We set this equal to zero: `3e^(2t)(1 + 2t) = 0-> t = -1/2`
Substitute `t = -1/2` into the parametric equations for x and y
Find x at `t = -1/2`:
`x = -1/2 + ln(-1/2 +1) = -1/2 + ln(1/2)~~ -1.19`
Find y at `= -1/2`
`y = 3(-1/2)e^(2(-1/2)) = -3/2e^-1 ~~-0.55`
Question 15

The diagram shows the curve with equation `y = sin2x + 3cos2x` for `0 ≤x≤ pi`. At the points P and Q on the curve, the gradient of the curve is `3`.
a. Find an expression for `(dy)/dx`.
b. By first expressing `(dy)/dx` in the form `Rcos(2x + alpha )`, where `R > 0` and `0≤x≤pi/2`, find the x- coordinates of P and Q, giving your answers correct to `4` s.f.
a.We are given the equation of the curve:
`y = sin2x + 3cos2x`
Find an expression for `(dy)/dx`
We can differentiate the given equation `y = sin2x + 3cos2x` with respect to `x`.
`(dy)/dx = 2cos2x – 6sin2x`
b.Express `(dy)/dx` in the form `Rcos(2x+alpha )`
We need to express the derivative in the form `Rcos(2x +alpha )`, where `R > 0` and `+alpha` is a phase shift.
`Rcos(2x + + alpha ) = R[cos(alpha)cos(2x) – sinalphasin2x]`
`Rcos(alpha) = 2 and Rsin(alpha) = 6`
To find R, use the identity:
`R = sqrt((2)^2+(6)^2) = sqrt(4+36) = 2sqrt10`
To find `alpha`, use the equation:
`tan(alpha) = frac{Rsinα}{Rcosα} = 6/2 = 3`
So `alpha`, = `tan^-1(3)`
`(dy)/dx = 2sqrt10cos(2x +alpha )`
Substitute `R = 2sqrt10` and `alpha= tan^-1(3)`
`2sqrt10cos (2x + tan^-1(3)) = 3`
`Cos(2x + tan^-1(3)) = 3/(2sqrt10) = 0.474`
`2x + tan^-1(3) = cos^-1(0.474)`
`2x + 1.249 = 1.079` or `2x + 1.249 = 2π – 1.079 = 5.204`
Solve out we have `x = -0.085` ( not valid) or `x = 1.978`
Since `0<= x<=pi` , the valid solutions are: `x = 1.978` radians
Question 16

The diagram shows the curve with equation `y = 5sin2x – 3tan2x` for values of x such that`0≤x≤pi/4`. Find the x-coordinates of the stationary point M, giving your answer correct to `3`s.f.
To find the stationary points, we need to find the derivative of y with respect to x, and set it equal to zero.
`y = 5sin2x – 3tan2x`
`(dy)/dx = 10cos2x – 6sec^(2)2x`
Set the derivative equal to zero: `(dy)/dx = 0`
`10cos2x – 6sec^(2)2x = 0`
`10cos^3(2x) – 6 = 0`
`cos(2x) = 0.843`
`2x = cos^-1(0.843)`
`x ~~0.284` radians
Question 17
The parametric equations of a curve are
`x = t^3 = 6t + 1, y = t^4 – 2t^3 + 4t^2 – 12t + 5`
a.Find `(dy)/dx` and use division to show that `(dy)/dx` can be written in the form `at + b`, where a and b are constants to be found.
b.The straight line `x -2y +9 = 0`is the normal to the curve at point P. Find the coordinates of P.
a.`x = t^3 = 6t + 1`
`y = t^4 - 2t^3 + 4t^2 - 12t + 5`
To find `(dy)/dx`, we first need to calculate `(dy)/dt` and `(dx)/dt`, then use the chain rule formula:
`(dx)/dt = 3t^2 + 6`
`(dy)/dt = 4t^3 - 6t^2 + 8t - 12`
`(dy)/dx = frac{4t^3 - 6t^2+ 8t - 12}{3t^2+6}`
Simplify `(dy)/(dx)` in the form `at + b`
`(dy)/dx = 4/3t - 2`
`a = 4/3` and `b = - 2`
b.`y = 1/2x + 9/2`
So, the gradient of the normal is `1/2`, and the gradient of the curve at point P is the negative reciprocal:
`(dy)/dx = - 2`
`(dy)/dx = 4/3t - 2 = - 2-> t = 0`
Substitute `t = 0` into the parametric equations for `x` and `y`:
`x = 0^3 + 6(0) + 1 = 1`
`y = 0^4 - 2(0^3) + 4(0^2) - 12(0) + 5 = 5`
The coordinates of point P are:`P = (1,5)`
Question 18

The diagram shows the curve with parametric equations
`x = 2 - cos2t`, `y = 2sin^3t + 3cos^3t + 1` for `0≤x≤pi/2`. The endpoints of the curve are `(1,4)` and `(3,3)`.
a.Show that `(dy)/dx` `= 3/2sint - 9/4cost`
b.Find the coordinates of the minimum point, giving each coordinate correct `3` s.f.
c.Find the exact gradient of the normal to the curve at the point for which `x =2`
a.`x = 2 – cos2t, y = 2sin^3t + 3cos^3t + 1`
`(dy)/dt = 6cos3t – 9sin3t`
`(dx)/dt = 2sin2t`
`(dy)/dx = frac{(dy)/dt}{(dx)/dt} =frac{ 6cos3t – 9sin3t }{ 2sin2t} = 3/2sint – 9/4cost`
b.Let `3/2sint – 9/4cost = 0`
`6sint = 9 cost`
`tan(t) = 3/2`
`t = 0.983` into the parametric equations for `x` and `y`
`x = 2 - cos2t = 2.38`
`y = 2sin^3t + 3cos^3t + 1 = 2.66`
So the coordinates of the minimum point are : `P(2.38, 2.66)`
c.Finding the exact gradient of the normal to the curve at `x = 2`
`x = 2 - cos2t`
`2 - cos2t = 2-> t =pi/ 4`
Find the gradient of the tangent at `t = pi/4`
From part a, the derivative of `y` with respect to `x` is:
`(dy)/dx = 3/2sint - 9/4cost`
Substitute `t = pi/4`
`sinfrac{pi}4 = cosfrac{pi}4 =sqrt 2/2`
`(dy)/dx = 3/2 x sqrt2/2– 9/4 xx sqrt2/2 = (-3sqrt2)/8`
The gradient of the normal `= -1/((dy)/dx) = 8/sqrt32 =(4sqrt2)/3`
Question 19
The equation of a curve is `x^2 + 4xy + 2y^2 = 7`.
a. Find the equation of the tangent to the curve at the point`(-1,3)`. Give your answer in the form `ax + by + c = 0` where `a`, `b` and `c` are integers.
b. Show that there is no point on the curve at which the gradient is `1/2`.
a.The equation of a curve is `x^2 + 4xy + 2y^2 = 7`.
Differentiate the given equation implicitly
Differentiate both sides with respect to `x` using implicit differentiation:
`d/dx(x^2) + d/dx(4xy) + d/dx(2y^2) = d/dx(7)`
Apply the product rule to `4xy`:
`2x + 4((dy)/dx x +y) + 4y(dy)/dx = 0`
`4x(dy)/dx + 4y(dy)/dx = -(2x + 4y)`
`(dy)/dx = frac{-(2x + 4y)}{4x+4y}`
Find the gradient at the point `(-1, 3)`, substitute `x = -1` and `y=3` into the expression for `(dy)/dx`
The result of `(dy)/dx = -5/4`
Find the equation of a line is given by:
`y - y_1 = m(x - x_1)`
Substitute `m= -5/4`, `x = -1` and `y = 3`
So the equation of the tangent line is: `5x + 4y - 7 = 0`
b.`(dy)/dx = frac{-(2x + 4y)}{4x+4y}`
Set the gradient equal to `1/2 = frac{-(2x + 4y)}{4x+4y}`
Simplify the equation we have: `8x + 12y = 0`
So `y = -2/3x` into the original curve equation `x^2 + 4xy + 2y^2 = 7`
We have that there is any condition is valid, which shows that no such point satisfies both the curve equation and the gradient condition.
There is no point on the curve where the gradient is `1/2`
Question 20

The diagram shows the part of the curve `y = 3e^-xsin2x` for `0≤x≤pi/2`, and the stationary point M.
a. Find the equation of the tangent to the curve at the origin.
b. Find the coordinates of M, giving each coordinate correct to `3` decimal places.
a.Use differentiate to find the tangent of the equation `(dy)/dx`
`y = 3e^-xsin2x`
`(dy)/dx = u'v + v'u = (3e^-x)’xxsin2x + (sin2x)’3e^-x`
`= -3e^-xsin2x + 2(cos2x)3e^-x`
The equation passes through the origin point O `(0,0)`
Substitute `x = 0` into `(dy)/dx = -3e^-0sin(2 xx 0) + 2(cos2 x 0)3e^-0 = 6`
So the slope of the tangent line at the origin is `6`.
The equation is peformed `y - y_1 = m(x - x_1)`
With`m = 6`, point `(0,0)`
`y = 6x`
b.Let `(dy)/dx =0-> -3e^-xsin2x + 2(cos2x)3e^-x = 0`
`2cos2x - sin2x = 0`
`2cos2x = sin2x`
`x = 0.554` radians
Substitute `x = 0.554` into the original equation `y = 3e^-xsin2x`
`y = 1.543`
Question 1
A curve hass parametric equations `x = e^t – 2e^-t, y = 3e^(2t) +1`
find the equation of the tangent to the curve at the point for which `t = 0`. [5]
Question 2
Find the exact coordinates of the stationary point on the curve with equation `y=5xe^(1/2x)` [5]
Question 3
The equation of a curve is `cos3x + 5siny = 3`
Find the gradient of the curve at the point `(pi/9, pi/6)` [5]
Question 4
A curve is defined by the parametric equations : `x = 3t - 2sint`, `y = 5t + 4cost`
Where `0<= t <=2π`. At each of the points P and Q on the curve, the gradient of the curve is `5/2`.
a.Show that the values of t at P and Q satisfy the equation `10cost – 8sint = 5` [3]
b.Express `10cost – 8sint` in the form Rcos`(t +alpha )`, where `R > 0` and `0 . Give the exact value of R and the value of `alpha` correct to `3`s.f.[4]
c.Hence find the values of t at the points P and Q. [4]
Question 5
The equation of a curve is `2e^(2x)y – y^3 + 4 = 0.`
a.Show that `(dy)/dx = frac{4ye^(2x)}{3y^2 -2e^(2x)}`. [4]
b.The curve passes through the point `(0,2)`.
Find the equaion of the tangent to the cruve ar this point, giving your answer in the for, `ax + by + c = 0`. [3]
Show that the curve has no stationary points [2]
Question 6
Find the equation of the normal to the curve `x^2lny + 2x + 5y = 11` at the point `(3,1)`.
Question 7
Find the exact coordinates of the stationary point of the curve with equation `y = (3x)/lnx`.
Question 8
A curve has equation `y = frac{3+ 2lnx}{ 1 + lnx}`. Find the exact gradient of the curve at the point for which`y = 4`.
Question 9
The equation of a curve is `x^2 – 4xy – 2y^2 = 1`.
a.Find an expression for `(dx)/dy` and show that the gradient of the curve at the point `(-1, 2)` is `-5/2`.
b.Show that the curve has no stationary points.
c.Find the x-coordinate of each of the points on the curve at which the tangent is parallel to the y – axis.
Question 10
The parametric equations of a curve are
`x =3sin2theta, y = 1 + 2tan2θ`, for `0<=theta<= pi/4`.
Find the exact gradient of the curve at the point for which `theta= pi/6`.
Find the value of `theta` at the point where the gradient of the curve is `2`, giving the value correct to `3` s.f.
Question 11
A curve has equation `y = 4xsin frac{1}{2} x`. Find the equation of the tangent to the curve at the point for which `x = pi`.
Question 12

The diagram shows part of the curve defined by the parametric equations
`x = t^2 + 4t, y = t^3 – 3t^2`
The curve has a minimum point at `M` and crosses the x-axis ar the point P.
a. Find the gradient of the curve at P.
b. Find the coordinates of the point M.
c.The value of the gradient of the curve at the point with parameter t is denoted by m. Show that `3t^2 – (2m + 6)t – 4m = 0` and hence find the set of possible values of `m` for points on the curve.
Question 13
A curve has equation `y = 3ln(2x + 9) -2lnx`.
a. Find the x-coordinates of the stationary point.
b. Determine whether the stationary point is a maximum or minimum point.
Question 14
A curve has parametric equations
`x = t + ln(t +1), y = 3te^(2t)`
a. Find the equation of the tangent to the curve at the origin.
b. Find the coordinates of the stationary point, giving each coordinate correct to `2` decimal places.
Question 15

The diagram shows the curve with equation `y = sin2x + 3cos2x` for `0 ≤x≤ pi`. At the points P and Q on the curve, the gradient of the curve is `3`.
a. Find an expression for `(dy)/dx`.
b. By first expressing `(dy)/dx` in the form `Rcos(2x + alpha )`, where `R > 0` and `0≤x≤pi/2`, find the x- coordinates of P and Q, giving your answers correct to `4` s.f.
Question 16

The diagram shows the curve with equation `y = 5sin2x – 3tan2x` for values of x such that`0≤x≤pi/4`. Find the x-coordinates of the stationary point M, giving your answer correct to `3`s.f.
Question 17
The parametric equations of a curve are
`x = t^3 = 6t + 1, y = t^4 – 2t^3 + 4t^2 – 12t + 5`
a.Find `(dy)/dx` and use division to show that `(dy)/dx` can be written in the form `at + b`, where a and b are constants to be found.
b.The straight line `x -2y +9 = 0`is the normal to the curve at point P. Find the coordinates of P.
Question 18

The diagram shows the curve with parametric equations
`x = 2 - cos2t`, `y = 2sin^3t + 3cos^3t + 1` for `0≤x≤pi/2`. The endpoints of the curve are `(1,4)` and `(3,3)`.
a.Show that `(dy)/dx` `= 3/2sint - 9/4cost`
b.Find the coordinates of the minimum point, giving each coordinate correct `3` s.f.
c.Find the exact gradient of the normal to the curve at the point for which `x =2`
Question 19
The equation of a curve is `x^2 + 4xy + 2y^2 = 7`.
a. Find the equation of the tangent to the curve at the point`(-1,3)`. Give your answer in the form `ax + by + c = 0` where `a`, `b` and `c` are integers.
b. Show that there is no point on the curve at which the gradient is `1/2`.
Question 20

The diagram shows the part of the curve `y = 3e^-xsin2x` for `0≤x≤pi/2`, and the stationary point M.
a. Find the equation of the tangent to the curve at the origin.
b. Find the coordinates of M, giving each coordinate correct to `3` decimal places.