Question 1
a.Prove that
`Sin2θ(cosec theta – sec theta ) -=sqrt8 cos(θ + 1/4pi)`
b.Solve the equation
`sin2θ("cosec" theta - sec theta ) = 1`
for `0 < theta < 1/2 pi`. Give the answer correct to `3` s.f
c.Find `intsinx("cosec"1/2x - sec frac{1}{2}x) dx`
Medium
Mark as Complete
Mark Scheme
Question 2
a.Find the quotient when `9x^3 – 6x^2 – 20x + 1` is divided by `(3x +2)`, and show that the remainder is `9`.
b.Hence find `int_2^6frac{9x^3 – 6x^2- 20x +1 }{ 3x +2} dx`, giving the answer in the form `a + ln`b where `a` and `b` are integers.
c.Find the exact root of the equation `9e^(9y) – 6e^(6y) – 20e^(3y) – 8 = 0`.
Easy
Mark as Complete
Mark Scheme
Question 3
It is given that `int_0^a(frac{4}{2x + 1 }+ 8x)dx = 10`, where `a` is a positive constant.
a.Show that `a = sqrt(2.5 –0.5ln (2a +1) )`
b.Using the equation in part (a), show by calculation that `1 < a < 2`
c.Use an iterative formula, based on the equation in part (a), to find the value of a correct to `4` s.f. Give the result of each iteration to `6` s.f.
Medium
Mark as Complete
Mark Scheme
Question 4
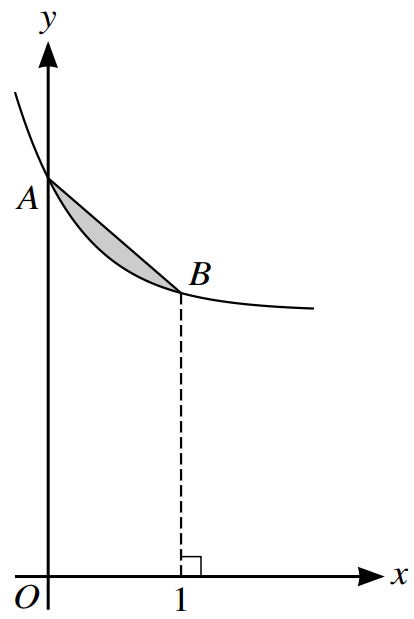
The diagram shows the curve `y = 2 + e^(-2x)`. The curve crosses the y-axis at the point A, and the point B on the curve has x-coordinate `1`. The shades region is bounded by the curve and the line segment AB.
Find the exact area of the shaded region.
Easy
Mark as Complete
Mark Scheme
Question 5
A curve has equation `y = f(x)` where `f(x) = frac{4x^3+8x -4}{2x -1}`
a.Find an expression for `(dy)/dx` and hence find the coordinates of each of the stationary points of the curve `y = f(x)`.
b.Divide `4x^3 + 8x – 4` by `(2x -1)`, and hence find `intf(x)dx`.
Easy
Mark as Complete
Mark Scheme
Question 6
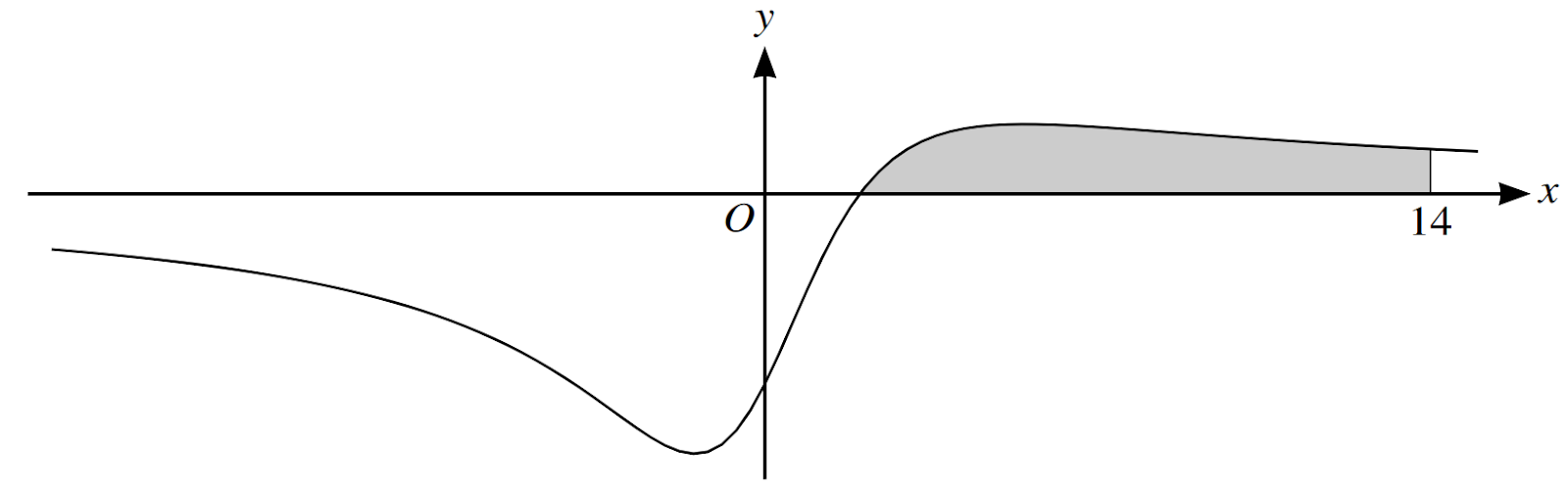
The diagram shows the curve with equation `y = frac{x -2}{x^2 + 8}`. The shaded region is bounded by the curve and the lines `x = 14` and `y = 0`.
a. Find `(dy)/dx` and hence determine the exact x-coordinates of the stationary points.
b. Use the trapezium rule with three intervals to find an approximation to the area of the shaded region. Give the answer correct to `2` s.f.
Easy
Mark as Complete
Mark Scheme
Question 7
a.Find `intfrac{8}{4x +1} + frac{8}{cos^2(4x +1)}dx`
b.It is given that `int_0^(pi/2)(3+4cos^2 frac{1}{2}x + ksin2x)dx = 10`
Find the exact value of the constant `k`.
Medium
Mark as Complete
Mark Scheme
Question 8
a.Show that `int_1^4(2/x +frac{2}{2x +1dx}) = ln48`
b.Find `intsin2x(cotx+2"cosec"x)dx`.
Medium
Mark as Complete
Mark Scheme
Question 9
a.Find the exact value of `int_0^(pi/2)(4sin2x+2"cox"^2x)dx`. Show all necessary working.
b.Use the trapezium rule with two intervals to find an approximation to `int_2^8 sqrt(ln (1 +x) )dx`.
Easy
Mark as Complete
Mark Scheme
Question 10
a.Find the Quotient and remainder when `2x^3 + x^2 – 8x` is divided by `(2x +1)`.
b.Hence find the exact value of `int_0^3frac{2x^3 + x^2 - 8x}{2x +1}dx`, giving the answer in the form `ln(ke^a)` where `k` and `a` constant.
Easy
Mark as Complete
Mark Scheme
Question 11
Find the exact value of `int_1^2(2e^(2x) – 1)^2dx`. Show all necessary working.
Easy
Mark as Complete
Mark Scheme
Question 12
a.Show that `int_2^18 frac{3}{2x}dx = ln27`.
b.Find the exact value of `int_0^(1/6pi)4sin^2 (3/2x)dx`. Show all necessary working.
Easy
Mark as Complete
Mark Scheme
Question 13
a. Use the trapezium rule with four intervals to find an approximation to `int_0^8ln(x+2)dx`, Giving your answer correct to `3` s.f.
b. Hence find an approximation to `int_0^8 3ln(x^2+4x+4)dx`.
Medium
Mark as Complete
Mark Scheme
Question 14
a.Express `5cos theta – 2sin theta`in the form `Rcos( + α)`
Where `R > 0` and `0 . Give the value of correct to `4` decimal places.
b.Using your answer from part (a), solve the equation `5cot theta – 4"cosec" theta = 2` for `0 < theta < 2pi`
c.Find `intfrac{1}{(5cosfrac{1}2x – 2sin frac{1}2x)^2} dx`
Hard
Mark as Complete
Mark Scheme
Question 15
a.Show that `2"cosec"^2 2x(1 – cos2x)_= sec^2x`.
b.Solve the equation `2"cosec"^2 2x(1 – cos2x) = tanx + 21`for `0 < x < pi`, giving your answers correct to `3` s.f.
c.Find `[2"cosec"^2(4y +2) –2"cosec"^2(4y + 2)cos(4y +2)]dy`.
Hard
Mark as Complete
Mark Scheme
Question 16
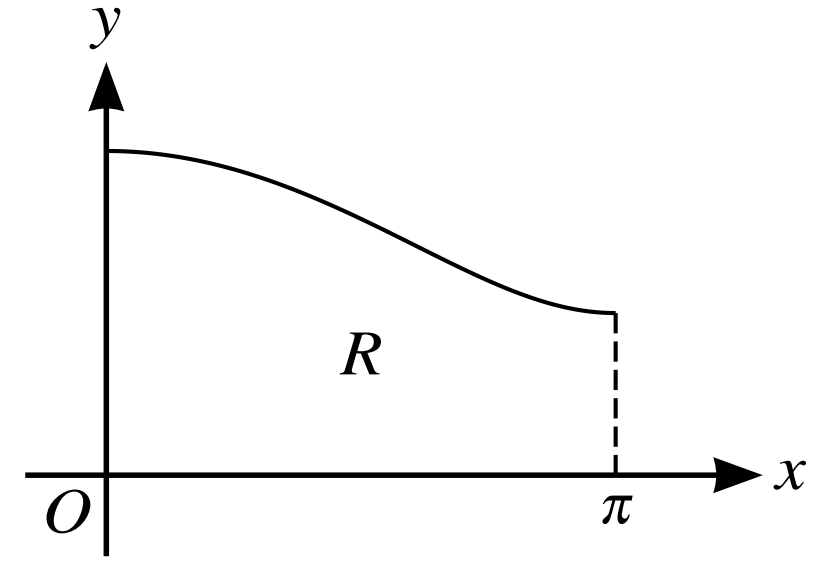
The diagram shows the curve with equation `y = sqrt(1 + 3cos^2(1/2x)))` for `0 <=x ≤π`. The region R is bounded by the curve, the axes and the line `x = pi`.
a. Use the trapezium rule with two intervals to find an approximation to the area of R, giving your answer correct to `3` s.f.
b. The region R is rotated completely about x-axis. Without using a calculator, find the exact volume of the solid produced.
Medium
Mark as Complete
Mark Scheme
Question 17
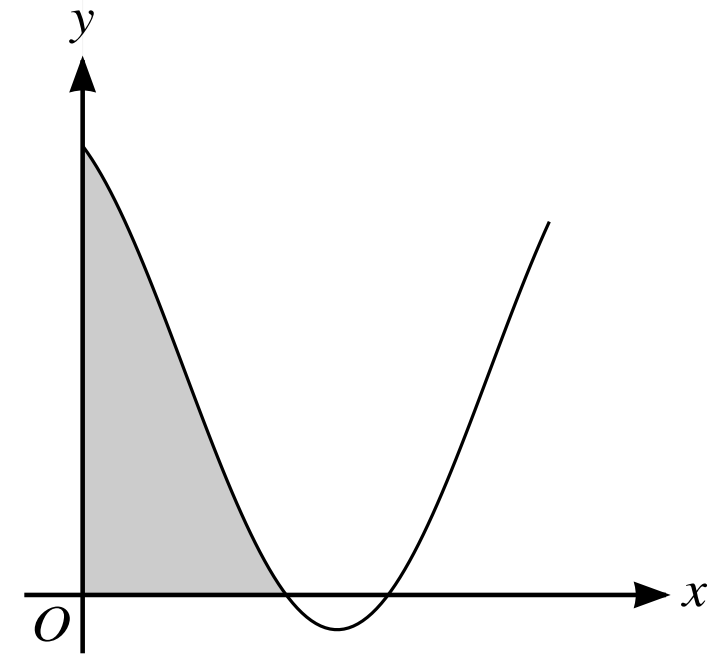
The diagram shows part of the curve)
`y = 2cos2xcos(2x + pi/6)`.
The shaded region is bounded by the curve and the two axes.
a.Show that `2cos2xcos(2x + pi/6)` can be expressed in the form `k_1(1 + cos4x) + k_2sin4x`,
where the values of the constant `k_1` and `k_2` are to be determined.
b.Find the exact area of the shaded region.
Hard
Mark as Complete
Mark Scheme
Question 18
a. Given that `int_0^a4e^(1/2x + 3)dx = 835`, find the value of the constant a correct to `3` s.f.
Easy
Mark as Complete
Mark Scheme
Question 19
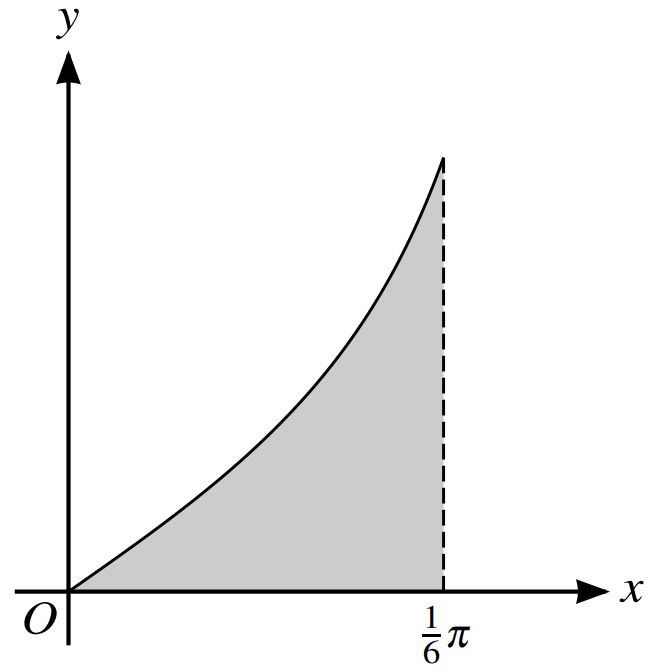
The diafram shows the curve `y = tan2x` for `0 <=x <=pi/6`. The shaded region is bounded by the curve and the lines`x = pi/6` and `y = 0`.
a. Use the trapezium rule with two intervals to find an approximation to the area of the shaded region, giving your answer correct to `3` s.f.
b. Find the exact volume of the solid formed when the shaded region is rotated completely about the x-axis.
Medium
Mark as Complete
Mark Scheme
Question 20
a. Find `intfrac{4 + sin^2 theta}{1 - sin^2 theta} d theta`.
b. Given that `int_0^afrac{2}{3x +1} dx = ln16`, find the value of the positive constant `a`.
Easy
Mark as Complete
Mark Scheme
Question 21
a. Find `intfrac{1 + cos^4 2x}{cos^2 2x}dx`
b. Without using a calculator, find the exact value of `int_4^14 (2 +frac{6}{3x -2} )dx`, giving your answer in the form`ln(aeb)^b`, where `a` and `b` are integers.
Medium
Mark as Complete
Mark Scheme
Question 1
a.Prove that
`Sin2θ(cosec theta – sec theta ) -=sqrt8 cos(θ + 1/4pi)`
b.Solve the equation
`sin2θ("cosec" theta - sec theta ) = 1`
for `0 < theta < 1/2 pi`. Give the answer correct to `3` s.f
c.Find `intsinx("cosec"1/2x - sec frac{1}{2}x) dx`
In LHS we have:
`Sin2θ("cosec" theta – sec theta )`
`= 2 sin theta cos theta (1/sinθ – 1/cosθ)`
`= 2 sintheta costheta ( frac{sin θ-cos θ}{2 sin θcos θ})`
`= 2cos θ – 2sin theta`
In RHS we have:
`sqrt8 cos(θ + 1/4pi)`
`= sqrt8(costhetacos frac{pi}4 – sin thetasinfrac{pi}4)`
`= sqrt8(costheta(sqrt(2)/2) - sin theta(sqrt2/2))`
`= frac{sqrt(2)sqrt(8)}2(cosθ- sintheta)`
`= 2cos θ – 2sin theta`
So LHR = RHS
b. `sqrt8 cos(θ + 1/4pi) = 1`
`cos (θ + pi/4) = 1/sqrt8`
`theta+ pi/4 = cos^-1(1/sqrt8)`
`theta= -pi/ 4 + cos^-1(1/sqrt8) = 0.424`
c.`sin2θ(cosec theta – sec theta ) -= sqrt8 cos(θ + 1/4pi)`
`sinx(cosecx/2 – secfrac{x}2) = sqrt8cos(x/2 + 1/4pi)`
`intsinx(cosecfrac{x}2 – secfrac{x}2)dx = int sqrt8(cos(x/2 + 1/4pi)dx`
`= sqrt8(frac{sin frac{x}2 +1/4pi}{ 1/2})`
`= 2sqrt8 sin(x/2 +1/4pi)`
Question 2
a.Find the quotient when `9x^3 – 6x^2 – 20x + 1` is divided by `(3x +2)`, and show that the remainder is `9`.
b.Hence find `int_2^6frac{9x^3 – 6x^2- 20x +1 }{ 3x +2} dx`, giving the answer in the form `a + ln`b where `a` and `b` are integers.
c.Find the exact root of the equation `9e^(9y) – 6e^(6y) – 20e^(3y) – 8 = 0`.
a. Uses long division, we have:
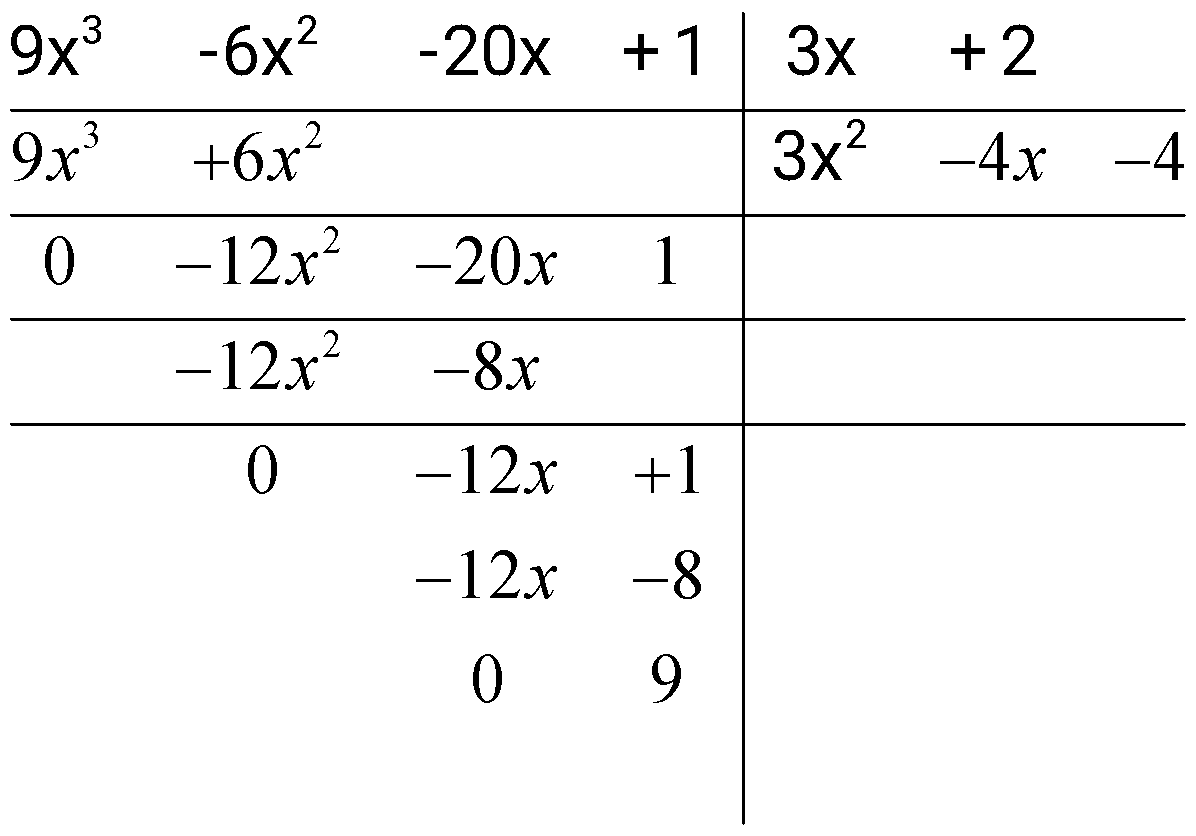
b. `int_1^6(3x^2-4x-4+ frac{9}{3x+2})dx`
`= [x^3 -2x^2 -4x+3ln u ]_1^6 + c`
`= (6^3 - 2(6)^2 - 4(6) + 3ln(20)) – (1^3 - 2(1)^2 - 4(1) + 3ln(5))`
`= 125 + 2ln4 = 125 + ln64`
`a = 125`
`b = 64`
c. `x = e^(3y)`
`9x^3 – 6x^2 – 20x – 8 = 0`
`9x^3 – 6x^2 – 20x – 8 = (3x +2)(3x^2 – 4x – 4)`
`= (3x + 2)(x – 2)(3x +2) = 0`
`3x +2 = 0-> x = -2/3-> e^(3y) = -2/3` (elimination)
`x -2 = 0-> x = 2 -> e^(3y) = -2/3 -> lne^(3y) = ln2-> y = 1/3ln2`
`3x + 2 = 0 -> x = -2/3 → e^(3y) = -2/3` (elimination)
Question 3
It is given that `int_0^a(frac{4}{2x + 1 }+ 8x)dx = 10`, where `a` is a positive constant.
a.Show that `a = sqrt(2.5 –0.5ln (2a +1) )`
b.Using the equation in part (a), show by calculation that `1 < a < 2`
c.Use an iterative formula, based on the equation in part (a), to find the value of a correct to `4` s.f. Give the result of each iteration to `6` s.f.
a.`[4 xx 1/2 ln(2x +1) + 8/2x^2]_0^a`
`= 4 xx 1/2 ln(2a +1) + 4a^2 = 10`
`a =sqrt( 2.5 -0.5ln (2a+1))`
b.When `a = 1`
`sqrt(2.5 -0.5ln (2a+1)) = 1`
`a = -0.397`
When `a = 2`
`sqrt(2.5 -0.5ln( 2a+1) = 2`
`sqrt(2.5 -0.5ln( 2a+1) = 2`
Sign changes, there is a root between `a = 1` and `a = 2`
Apply an iterative formula and choose `a_0 = 1.5`, (or any number) that between `1 < a < 2`
`a_1 = sqrt( 2.5 -0.5ln (2 x 1.5+1)) = 1.34419`
`a_2 =sqrt( 2.5 -0.5ln (2 x( 1.34419)+1)) = 1.35919`
`a_3 = sqrt(2.5 -0.5ln (2 x( 1.35919)+1)) = 1.35770`
`a_4 = sqrt(2.5 -0.5ln (2 x( 1.35770)+1)) = 1.35785`
`a_5 = sqrt(2.5 -0.5ln (2 x( 1.35785)+1)) = 1.35784`
So `a = 1.358`
Question 4

The diagram shows the curve `y = 2 + e^(-2x)`. The curve crosses the y-axis at the point A, and the point B on the curve has x-coordinate `1`. The shades region is bounded by the curve and the line segment AB.
Find the exact area of the shaded region.
To solve this problem step by step, we need to calculate the exact area of the shaded region between the curve `y=2+e^(-2x)` and the straight line segment AB.
From the coordinates of point A and B, find the equation.
At point A, `x = 0`, substitute it into `y = 2+e^(-2x)`, so `y = 3`
At point B,`x =1`, substitute it into `y = 2+e^(-2x)`, so `y = 2 + e^-2`
Therefore, B `(1, 2+e^(-2))`
Find the equation AB: `y = (e^-2 – 1)x + 3`
The area of the shaded region between the curve and the line from `x=0` to `x=1` is given by the integral of the difference between the curve and the line:
`int_0^1[(2 + e^(-2x)) – ((e^-2 –1)x + 3)]dx`
So the area `= (1/2 – e^-2/2) – frac{(e^-2–1)}{ 2} – 1`
`= e^-2`
Question 5
A curve has equation `y = f(x)` where `f(x) = frac{4x^3+8x -4}{2x -1}`
a.Find an expression for `(dy)/dx` and hence find the coordinates of each of the stationary points of the curve `y = f(x)`.
b.Divide `4x^3 + 8x – 4` by `(2x -1)`, and hence find `intf(x)dx`.
a. Use long division to simplify the rational function
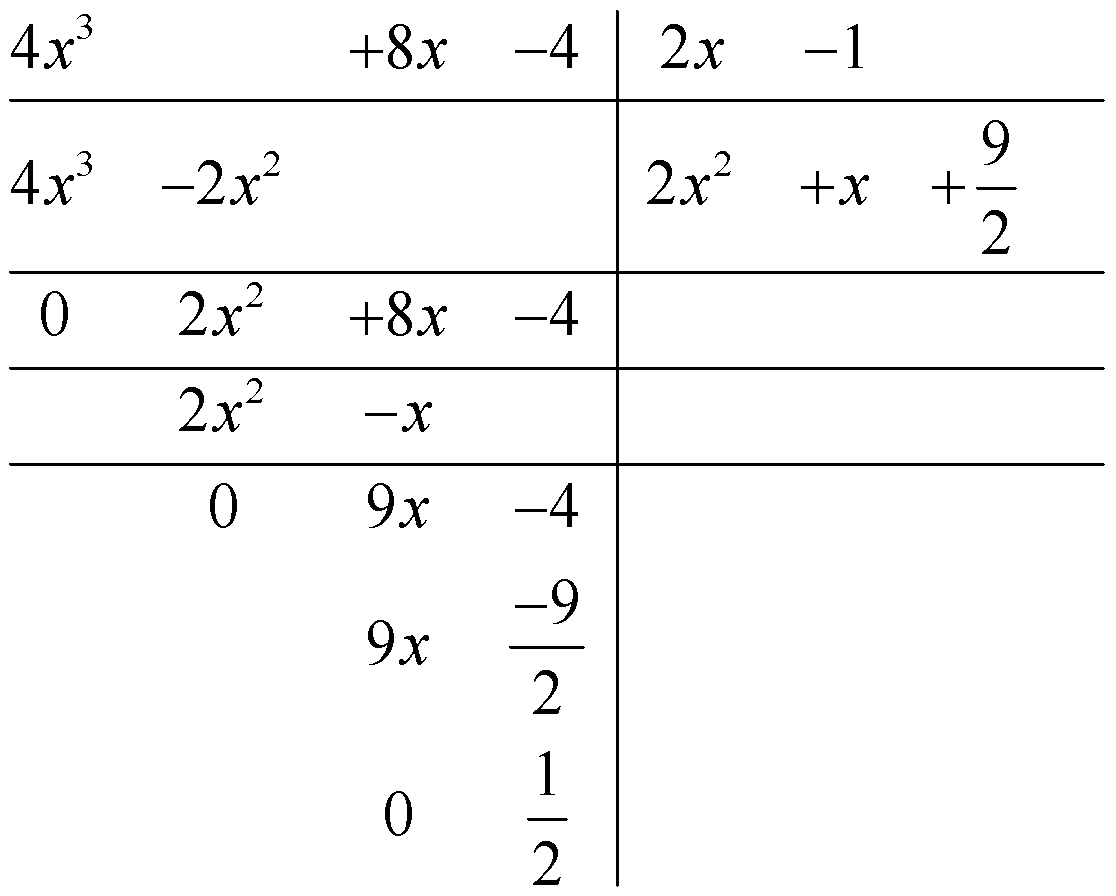
`(dy)/dx = (2x^2 + x + 9/2 + frac{1}{2(2x -1)})’`
`= 4x + 1 + frac{-4}{(4x -2)^2}`
To find stationary point, take `(dy)/dx = 0`
`4x + 1 +frac{ -4}{(4x -2)^2} = 0`
`(4x +1)(4x -2)^2 – 4 = 0`
`4x^2(4x -3) = 0`
`x = 0 ->` substitute into `f(x)`, we have `y = 4`
`x = 3/ 4 ->` substitute into f(x), we have `y = 59/8`
b.`int(2x^2 + x + 9/2 + frac{1}{2(2x -1)})dx`
`= (2x^3)/3 + (x^2)/2 + (9x)/2 + 1/4ln|2x -1| + C`
Question 6

The diagram shows the curve with equation `y = frac{x -2}{x^2 + 8}`. The shaded region is bounded by the curve and the lines `x = 14` and `y = 0`.
a. Find `(dy)/dx` and hence determine the exact x-coordinates of the stationary points.
b. Use the trapezium rule with three intervals to find an approximation to the area of the shaded region. Give the answer correct to `2` s.f.
a.`(dy)/dx = frac{(x - 2)'(x^2+8) -(x^2+8)'}{(x^2+8)^2} =frac{ -x^2 + 4x + 8}{ (x^2+8)^2}`
Find the stationary point by taking `(dy)/dx = 0`
`-x^2 + 4x + 8 = 0`
So`x = 2 + 2sqrt3` and `x = 2 - 2sqrt3`
b.The trapezium rule is given by:
Area `= h/2 [y_o + 2(y_1 + y_2 + …..+ y_(n-1)) + y_n]`
Use y values `(0), 4/44, 8/108, 12/204` or decimal equivalents
Use correct formula, or equivalent, with `h = 4`
Area `= 4/2 (0 + 2x4/44 + 2x8/108 + 12/204) = 0.78`
Question 7
a.Find `intfrac{8}{4x +1} + frac{8}{cos^2(4x +1)}dx`
b.It is given that `int_0^(pi/2)(3+4cos^2 frac{1}{2}x + ksin2x)dx = 10`
Find the exact value of the constant `k`.
a.`intfrac{8}{4x +1}dx +intfrac{ 8}{cos^2 4x +1}dx`
`int8/(4x +1)dx = 8/4ln(4x +1) = 2ln(4x +1)`
`int8/(cos^2 4x +1)dx = 8intsec^2(4x +1)dx =8 xx 1/4tan(4x +1) = 2tan(4x +1)`
Combine the result, we have:
`int8/(4x +1)dx + int8/(cos^2(4x +1))dx = 2ln(4x +1) + 2tan(4x +1)`
b.`int_0^ (pi/2)(3+4cos^2 frac{1}{2}x + ksin2x)dx = 10`
`int_0^(pi/2)(3)dx = (3π)/2`
`int_0^(pi/2)(4cos^2frac{1}{2}x)dx = 4int _0^(pi/2)((1 + cosx)/2)dx = pi+ 2`
`int_0^(pi/2)(ksin2x)dx = k`
`(3π)/2 + pi + 2+ k = 10`
So `k = 8 - (5π)/2`
Question 8
a.Show that `int_1^4(2/x +frac{2}{2x +1dx}) = ln48`
b.Find `intsin2x(cotx+2"cosec"x)dx`.
a.`int_1^4(2/x + frac{2}{2x +1})dx = int_1^4 2/xdx + int_1^4 frac{2}{2x+1}dx`
`int_1^4 frac{2}{2x+1}dx = 2ln4 – 2ln1 = 2ln4`
`int_1^4 frac{2}{2x+1}dx = ln9 – ln3 = lnfrac{ 9}{3} = ln3`
Combine the result, we have:
`int_1^4 frac{2}{x}dx + int_1^4 frac{2}{2x+1}dx = 2ln4 + ln3 = ln(16xx3) = ln48`
b.`intsin2x(cotx+2cscx)dx=intsin2xcotxdx+ 2intsin2xcscxdx`
Use the identity `cotx = frac{cos x}{sinx}`, so:
`intsin2xfrac{cosx}{sinx}dx = intfrac{2sinxcos^2x}{sinx}dx =int 2cos^2xdx = int(1+ cos2x)dx`
`= x + 1/2sin2x + C`
Use the identity `cscx = 1/sinx`, so:
`2intsin2x frac{1}{sinx}dx = 2intfrac{sin2x}{sinx}dx = 2intfrac{sin2x}sinxdx = intfrac{2sinxcosx}sinxdx = 4sinx + C`
`intsin2x(cotx+2cscx)dx = x + 1/2sin2x + 4sinx + C`
Question 9
a.Find the exact value of `int_0^(pi/2)(4sin2x+2"cox"^2x)dx`. Show all necessary working.
b.Use the trapezium rule with two intervals to find an approximation to `int_2^8 sqrt(ln (1 +x) )dx`.
a.`int_0^2 (4sin2x+2"cox"^2x)dx =int_0^(pi/2)( 4sin2x)dx + int_0^(pi/2)(2"cox"^2x)dx`
`int_0^(pi/2)(4sin2x)dx = 4/2 [-cos2x]_0^(pi/2) = -2[(-1) -1] = 4`
`int_0^(pi/2)(2"cox"^2x)dx =int_ 0^(pi/2)2(frac{1+ cos2x}{2})dx = int_0^(pi/2)(1 + cos2x) dx`
`=pi/ 2`
Combine the result, we have:
`int_0^2 (4sin2x+2"cox"^2x)dx =4+pi/2`
b.`int_2^8sqrt((ln (1 +x)) dx` is using the trapezium rule with two intervals.
The interval is from`2` to `8`, so the points are `x_o = 2`, `x_1 = 5` (midpoint), and `x_2 = 8`.
The width of each interval h is:
`h = frac{8 - 2}{2} = 3`
Call `f(x) = sqrt(ln(1+x))`
`f(2) = sqrtln3`
`f(5) =sqrt ln6`
`f(8) =sqrt ln9`
The trapezium rule for two intervals is given by:
`int_2^8f(x)dx~~ h/2[f(x_o) + 2f(x_1) + f(x_n)]`
`int_2^8sqrtln(1+x)dx = 3/2[sqrtln3 + 2sqrtln6 + sqrtln9] = 7.81`
Question 10
a.Find the Quotient and remainder when `2x^3 + x^2 – 8x` is divided by `(2x +1)`.
b.Hence find the exact value of `int_0^3frac{2x^3 + x^2 - 8x}{2x +1}dx`, giving the answer in the form `ln(ke^a)` where `k` and `a` constant.
a.
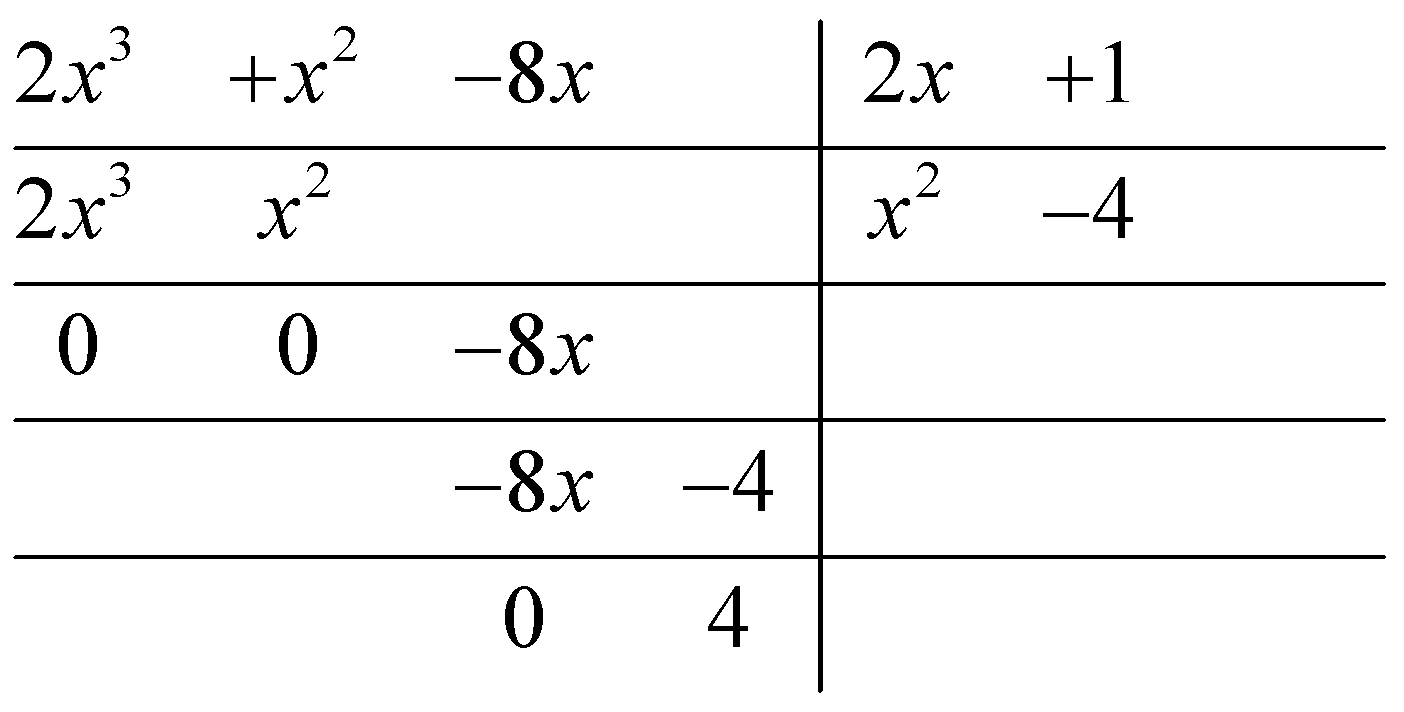
Quotient :`x^2 – 4`
Remainder: `4`
b.`int_0^3 frac{2x^3 + x^2 - 8x}{2x +1}dx =int _0^3(x^2 -4)dx + int_0^3frac{ 4}{2x +1}dx`
`int_0^3(x^2 -4)dx = [(x^3)/3 – 4x]_0^3 = -3`
`int_0^3 frac{4}{2x +1}dx = 4/2[ln(2x+1)]_0^3 = 2ln7`
Combine the result, we have:
`int_0^3 frac{2x^3 + x^2 - 8x}{2x +1}dx = -3 + 2ln7 = ln(e^-3) + ln(7^2) = ln(49/(e^3))`
`k =49` and`a = -3`.
Question 11
Find the exact value of `int_1^2(2e^(2x) – 1)^2dx`. Show all necessary working.
Expand the square
`(2e^(2x) -1)^2 = (2e^(2x))^2 – 2x2e^(2x)xx1 +1^2 = 4e^(4x) – 4e^(2x) + 1`
`int_1^2(4e^(4x) -4e^(2x) +1)dx = [4/4e^(4x) -4/2e^(2x) + x]_1^2 = e^8 – 3e^4 + 2e^2 +1`
Question 12
a.Show that `int_2^18 frac{3}{2x}dx = ln27`.
b.Find the exact value of `int_0^(1/6pi)4sin^2 (3/2x)dx`. Show all necessary working.
a.`int_2^18 3/(2x)dx = 3/2[lnx]_2^18 = 3/2(ln18 – ln2) = 3/2ln9 = ln27`
`int_0^(1/6pi)4sin^2 (3/2x)dx = int_0^(pi/6)4 xfrac{ 1 - cos(3x)}{2}dx`
`2int_0^(pi/6) (1 -cos(3x))dx = 2 [x - 1/3sin(3x)]_0^(pi/6) = frac{π -2}{3}`
Question 13
a. Use the trapezium rule with four intervals to find an approximation to `int_0^8ln(x+2)dx`, Giving your answer correct to `3` s.f.
b. Hence find an approximation to `int_0^8 3ln(x^2+4x+4)dx`.
a. The width of each interval h is:
`h = frac{8 -0}4 = 2`
Evaluate the function ln(x+2), we have:

The trapezium rule for two intervals is given by:
`int_0^8f(x)dx~~ h/2[f(x_o) + 2f(x_1) + 2f(x_2)+ 2f(x_2)+ 2f(x_3)+f(x_4)]`
`int_0^8ln(x+2)dx= 2/2[ln2 + 2ln4 + 2ln6 + 2ln8 + ln10] = 13.5`
b. `int_0^8 3ln(x^2+4x+4)dx`
We have: `x^2+4x+4 = (x +2)^2`
`3ln(x^2+4x+4) = 3ln(x+2)^2 = 6ln(x+2)`
`int_0^8 3ln(x^2+4x+4)dx = 6int_0^8 ln(x+2)dx = 6 xx13.5 = 81.0`
Question 14
a.Express `5cos theta – 2sin theta`in the form `Rcos( + α)`
Where `R > 0` and `0 . Give the value of correct to `4` decimal places.
b.Using your answer from part (a), solve the equation `5cot theta – 4"cosec" theta = 2` for `0 < theta < 2pi`
c.Find `intfrac{1}{(5cosfrac{1}2x – 2sin frac{1}2x)^2} dx`
a.`Rcos( theta + α) = Rcos theta cos alpha - Rsin theta sin alpha`
From the expression,`5cos theta – 2sin theta`, we have: `Rcos alpha = 5` and `Rsin alpha = 2`
`R^2cos^2alpha + R^2sin^2alpha = 25 + 4 = 29`
`R^2(cos^2alpha + sin^2 alpha ) = 29-> R = sqrt29`
`Tan alpha = 2/5 -> α = tan^-1(2/5) = 0.3805`
`5cos theta – 2sin theta = sqrt29cos( theta+ 0.3805)`
b.`5cot theta – 4"cosec" theta = 2`
`5frac{costheta}{sintheta} - 4frac{1}{sintheta} = 2`
`5cos theta - 2sintheta = 4`
From part (a), we have: `5cos theta - 2sin theta =sqrt 29cos( theta+ 0.3805)`
So the equation becomes:
`sqrt29cos( theta + 0.3805) = 4`
`theta+ 0.3805 = cos^-1(4/sqrt29) + k2pi`(cosine is positive in the first and fourth quadrants)
`theta` has the interval `0 < theta < 2 pi`, to solve out `theta~~ 0.3523` rad and `theta ~~ 5.1699` rad.
c.`intfrac{1}{(5cosfrac{1}{2}x – 2sinfrac{1}{2}x)^2}dx`
`5cosfrac{1}{2}x – 2sinfrac{1}{2}x =sqrt 29cos(1/2x + 0.3805)`
`intfrac{1}{(sqrt29cos(1/2x + 0.3805))^2} dx = 1/29sec^2(1/2x+0.3805)dx`
`= 1/29 xx 2tan(1/2x + 0.3805) + C`
`= 2/29(tanfrac{1}{2}x + 0.3805) + C`
Question 15
a.Show that `2"cosec"^2 2x(1 – cos2x)_= sec^2x`.
b.Solve the equation `2"cosec"^2 2x(1 – cos2x) = tanx + 21`for `0 < x < pi`, giving your answers correct to `3` s.f.
c.Find `[2"cosec"^2(4y +2) –2"cosec"^2(4y + 2)cos(4y +2)]dy`.
a.`csc^2theta = 1 + cot^2theta`and `sec^2theta = 1 + tan^2 theta`
`2csc^2 2x (1 – cos2x) = (2csc^2 2x) x (2sin^2x) = 4 csc^2 2x sin^2x`
But `csc2x = frac{1}{sin2x}`, we have:
`4 xx frac{1}{sin^2 2x} xx sin^2x = frac{4sin^2x}{sin^2 2x} = frac{4sin^2x}{(2sinxcosx)^2} = frac{1}{(cosx)^2} = sec^2x`
b.`2"cosec"^2 2x(1 – cos2x) = tanx + 21`
Use the result in part (a), we have:
`sec^2x = tanx + 21`
Question 16

The diagram shows the curve with equation `y = sqrt(1 + 3cos^2(1/2x)))` for `0 <=x ≤π`. The region R is bounded by the curve, the axes and the line `x = pi`.
a. Use the trapezium rule with two intervals to find an approximation to the area of R, giving your answer correct to `3` s.f.
b. The region R is rotated completely about x-axis. Without using a calculator, find the exact volume of the solid produced.
a.The trapezium rule is used to approximate the area under a curve. The rule states:
Area `~~h/2 [y_o + y_n + 2(y_1 + y_2 + ….. + y_(n-1))]`
The curve equation is `y =sqrt( 1+3cos^2 (1/2x))`
The interval `[0; pi]`is given with `n =2`.
`h = frac{π -0}{2} =pi/2`
Determine the x-values:
`x_o = 0`
`x_1 = pi/2`
`x2 = pi`
So `y_o = sqrt(1+3cos^2 (1/2x0)) = 2`
`y_1 = sqrt(1+3cos^2 (1/2xpi/2)) = sqrt2.5`
`y_2 = sqrt(1+3cos^2(1/2xπ) = 1`
Apply the trapezium rule
Area`~~pi/4[ 3+ 2xsqrt2.5]~~ 4.84`
b.`V =pi int_a^b y^2dx`
`y =sqrt( 1+3cos^2 (1/2x)), y^2 = 1 + 3cos^2(1/2x)`
`V = pi [int_0^pi 1dx + 3 int_3^pi cos^2(1/2x)dx]`
`int_0^pi1dx =pi`
`int_0^pi cos^2(1/2x)dx = 1/2int_0^pi[1+cos(x)]dx = 1/2[pi + 0] = pi/2`
Combine the result:
`V = pi[ pi+3 xx pi/ 2 ] = frac{5pi^2}{2}`
Question 17

The diagram shows part of the curve)
`y = 2cos2xcos(2x + pi/6)`.
The shaded region is bounded by the curve and the two axes.
a.Show that `2cos2xcos(2x + pi/6)` can be expressed in the form `k_1(1 + cos4x) + k_2sin4x`,
where the values of the constant `k_1` and `k_2` are to be determined.
b.Find the exact area of the shaded region.
a.Use the product – to –sum identities for trigonometric functions:
`cosAcosB = 1/2[cos(A -B) + cos(A+B)]`
`A = 2x`
B = 2x +6`B = 2x +pi/6`
`cos2xcos(2x +pi/6) = 1/2[cos(2x –(2x +pi/6)) + cos(2x+(2x +pi/6))]`
`= 1/2[cos(–pi/6) + cos(4x +pi/6)]`
`cos(–pi/6) = cos(pi/6) = sqrt3/2`
`cos2xcos(2x +pi/6) = 1/2[sqrt3/2 + cos(4x +pi/6)]`
with `cos(4x +pi/6) = cos4xcosfrac{pi}6 - sin4xsin6frac{pi}6 (sinfrac{pi}6 = 1/2)`
`2cos2xcos(2x +pi/6) = sqrt3/2 + sqrt3/2cos4x - 1/2sin4x`
`= sqrt3/2 (1+ cos4x) - 1/2sin4x`
`k_1 = sqrt3/2`, `k_2 = -1/2`
b. `y = 2cos2xcos(2x + pi/6) → y = sqrt3/2 (1+ cos4x) - 1/2sin4x`
Area `= int_0^(pi/6)(sqrt3/2(1 + cos4x) -1/2sin4x)dx`
Area `= sqrt3/2int_0^(pi/6)(1 + cos4x)dx - 1/2int_0^(pi/6)(sin4x)dx`
Area `= sqrt3/2[ x + frac{sin4x}{4}]_0^(pi/6) - 1/2[-frac{cos4x}{4}]_0^(pi/6)`
`= sqrt3/2[pi/6 + frac{sinfrac{2π}{3}}{4}] - 1/2 [-frac{frac{cos2π}{3}}{4}]`
Question 18
a. Given that `int_0^a4e^(1/2x + 3)dx = 835`, find the value of the constant a correct to `3` s.f.
`int_0^a4e^(1/2x + 3)dx = 835`
`int_0^a4e^(1/2x + 3)dx = 4e^(3int_0^ae^(1/2x)) dx = 4e^3[ 2e^(1/2x]]_0^a = 4e^3(2e^(1/2a) -2)`
`4e^3(2e^(1/2a) -2) = 835`
Find `a = 3.65`
Question 19

The diafram shows the curve `y = tan2x` for `0 <=x <=pi/6`. The shaded region is bounded by the curve and the lines`x = pi/6` and `y = 0`.
a. Use the trapezium rule with two intervals to find an approximation to the area of the shaded region, giving your answer correct to `3` s.f.
b. Find the exact volume of the solid formed when the shaded region is rotated completely about the x-axis.
The trapezium rule is used to approximate the area under a curve. The rule states:
Area `~~h/2 [y_o + y_n + 2(y_1 + y_2 + ….. + y_(n-1))]`
`h =frac{ pi/6-0}2 = pi/12`
`x_o = 0, x_1 = pi/12, x_2 = pi/6`
`y_o = tan(2 xx 0) = 0`
`y_1 = tan(2xpi/12) = 1/sqrt3`
`y_3 = tan(2 xx pi/6) = sqrt3`
Area `~~pi/24 xx 2.886 ~~0.378`
b.`V = piint_0^(pi/6)tan^2(2x)dx`
`tan^2(2x) = "sec"^2(2x) – 1`
`V = pi int_0^(pi/6)("sec"^2(2x) – 1)dx`
`V = pi (sqrt3/2 – pi/6)`
Question 20
a. Find `intfrac{4 + sin^2 theta}{1 - sin^2 theta} d theta`.
b. Given that `int_0^afrac{2}{3x +1} dx = ln16`, find the value of the positive constant `a`.
a. `intfrac{4 + sin^2 theta}{1 - sin^2 theta }d theta`
`1 - sin^2 theta = cos^2 theta`
`intfrac{4 + sin^2 theta}{ cos^2 theta} d theta`
`int frac{4 }{cos^2 theta} d + intfrac{sin^2 theta }{cos^2 theta} d theta`
`int frac{4 }{cos^2 theta }d = 4tan theta + C`
`int frac{sin^2 theta}{ cos^2 theta} d theta = int tan^2 theta d theta = tan theta - theta + C`
`int frac{4 + sin^2 theta}{1 - sin^2 theta} d theta = 5tan theta - theta + C`
b. `int_0^a frac{2}{3x +1}dx = ln16`
`2/3[ln(3x +1)]_0^a = ln16`
`ln(3a +1) = 3/2ln16`
`3a + 1 = 16^(3/2)`
`a = 21`
Question 21
a. Find `intfrac{1 + cos^4 2x}{cos^2 2x}dx`
b. Without using a calculator, find the exact value of `int_4^14 (2 +frac{6}{3x -2} )dx`, giving your answer in the form`ln(aeb)^b`, where `a` and `b` are integers.
a.`int frac{1 + cos^4 2x}{cos^2 2x}dx`
`int frac{1}{cos^2(2x)}dx + int frac{cos^4(2x)}{cos^2(2x)}dx`
`= int "sec"^2(2x)dx+ intcos^2(2x)dx`
`= sec^2(2x)dx = 1/2tan(2x) + C`
`int cos^2(2x)dx = int frac{ 1+ cos(4x)}{2}dx = 1/2x + 1/8sin4x + C`
Combine the results
`int frac{1 + cos^4 2x}{cos^2 2x}dx = 1/2tan2x + 1/2x + 1/8sin4x + C`
b. `int_4^14(2+frac{6}{3x-2})dx = 20 + 2ln4 = ln(e^24 xx 4^2) = ln(e^20x16) = ln(16e^20)`
So `a = 16` and `b = 20`.
Question 1
a.Prove that
`Sin2θ(cosec theta – sec theta ) -=sqrt8 cos(θ + 1/4pi)`
b.Solve the equation
`sin2θ("cosec" theta - sec theta ) = 1`
for `0 < theta < 1/2 pi`. Give the answer correct to `3` s.f
c.Find `intsinx("cosec"1/2x - sec frac{1}{2}x) dx`
Question 2
a.Find the quotient when `9x^3 – 6x^2 – 20x + 1` is divided by `(3x +2)`, and show that the remainder is `9`.
b.Hence find `int_2^6frac{9x^3 – 6x^2- 20x +1 }{ 3x +2} dx`, giving the answer in the form `a + ln`b where `a` and `b` are integers.
c.Find the exact root of the equation `9e^(9y) – 6e^(6y) – 20e^(3y) – 8 = 0`.
Question 3
It is given that `int_0^a(frac{4}{2x + 1 }+ 8x)dx = 10`, where `a` is a positive constant.
a.Show that `a = sqrt(2.5 –0.5ln (2a +1) )`
b.Using the equation in part (a), show by calculation that `1 < a < 2`
c.Use an iterative formula, based on the equation in part (a), to find the value of a correct to `4` s.f. Give the result of each iteration to `6` s.f.
Question 4

The diagram shows the curve `y = 2 + e^(-2x)`. The curve crosses the y-axis at the point A, and the point B on the curve has x-coordinate `1`. The shades region is bounded by the curve and the line segment AB.
Find the exact area of the shaded region.
Question 5
A curve has equation `y = f(x)` where `f(x) = frac{4x^3+8x -4}{2x -1}`
a.Find an expression for `(dy)/dx` and hence find the coordinates of each of the stationary points of the curve `y = f(x)`.
b.Divide `4x^3 + 8x – 4` by `(2x -1)`, and hence find `intf(x)dx`.
Question 6

The diagram shows the curve with equation `y = frac{x -2}{x^2 + 8}`. The shaded region is bounded by the curve and the lines `x = 14` and `y = 0`.
a. Find `(dy)/dx` and hence determine the exact x-coordinates of the stationary points.
b. Use the trapezium rule with three intervals to find an approximation to the area of the shaded region. Give the answer correct to `2` s.f.
Question 7
a.Find `intfrac{8}{4x +1} + frac{8}{cos^2(4x +1)}dx`
b.It is given that `int_0^(pi/2)(3+4cos^2 frac{1}{2}x + ksin2x)dx = 10`
Find the exact value of the constant `k`.
Question 8
a.Show that `int_1^4(2/x +frac{2}{2x +1dx}) = ln48`
b.Find `intsin2x(cotx+2"cosec"x)dx`.
Question 9
a.Find the exact value of `int_0^(pi/2)(4sin2x+2"cox"^2x)dx`. Show all necessary working.
b.Use the trapezium rule with two intervals to find an approximation to `int_2^8 sqrt(ln (1 +x) )dx`.
Question 10
a.Find the Quotient and remainder when `2x^3 + x^2 – 8x` is divided by `(2x +1)`.
b.Hence find the exact value of `int_0^3frac{2x^3 + x^2 - 8x}{2x +1}dx`, giving the answer in the form `ln(ke^a)` where `k` and `a` constant.
Question 11
Find the exact value of `int_1^2(2e^(2x) – 1)^2dx`. Show all necessary working.
Question 12
a.Show that `int_2^18 frac{3}{2x}dx = ln27`.
b.Find the exact value of `int_0^(1/6pi)4sin^2 (3/2x)dx`. Show all necessary working.
Question 13
a. Use the trapezium rule with four intervals to find an approximation to `int_0^8ln(x+2)dx`, Giving your answer correct to `3` s.f.
b. Hence find an approximation to `int_0^8 3ln(x^2+4x+4)dx`.
Question 14
a.Express `5cos theta – 2sin theta`in the form `Rcos( + α)`
Where `R > 0` and `0 . Give the value of correct to `4` decimal places.
b.Using your answer from part (a), solve the equation `5cot theta – 4"cosec" theta = 2` for `0 < theta < 2pi`
c.Find `intfrac{1}{(5cosfrac{1}2x – 2sin frac{1}2x)^2} dx`
Question 15
a.Show that `2"cosec"^2 2x(1 – cos2x)_= sec^2x`.
b.Solve the equation `2"cosec"^2 2x(1 – cos2x) = tanx + 21`for `0 < x < pi`, giving your answers correct to `3` s.f.
c.Find `[2"cosec"^2(4y +2) –2"cosec"^2(4y + 2)cos(4y +2)]dy`.
Question 16

The diagram shows the curve with equation `y = sqrt(1 + 3cos^2(1/2x)))` for `0 <=x ≤π`. The region R is bounded by the curve, the axes and the line `x = pi`.
a. Use the trapezium rule with two intervals to find an approximation to the area of R, giving your answer correct to `3` s.f.
b. The region R is rotated completely about x-axis. Without using a calculator, find the exact volume of the solid produced.
Question 17

The diagram shows part of the curve)
`y = 2cos2xcos(2x + pi/6)`.
The shaded region is bounded by the curve and the two axes.
a.Show that `2cos2xcos(2x + pi/6)` can be expressed in the form `k_1(1 + cos4x) + k_2sin4x`,
where the values of the constant `k_1` and `k_2` are to be determined.
b.Find the exact area of the shaded region.
Question 18
a. Given that `int_0^a4e^(1/2x + 3)dx = 835`, find the value of the constant a correct to `3` s.f.
Question 19

The diafram shows the curve `y = tan2x` for `0 <=x <=pi/6`. The shaded region is bounded by the curve and the lines`x = pi/6` and `y = 0`.
a. Use the trapezium rule with two intervals to find an approximation to the area of the shaded region, giving your answer correct to `3` s.f.
b. Find the exact volume of the solid formed when the shaded region is rotated completely about the x-axis.
Question 20
a. Find `intfrac{4 + sin^2 theta}{1 - sin^2 theta} d theta`.
b. Given that `int_0^afrac{2}{3x +1} dx = ln16`, find the value of the positive constant `a`.
Question 21
a. Find `intfrac{1 + cos^4 2x}{cos^2 2x}dx`
b. Without using a calculator, find the exact value of `int_4^14 (2 +frac{6}{3x -2} )dx`, giving your answer in the form`ln(aeb)^b`, where `a` and `b` are integers.