Question 1
a) By sketching a suitable pair of graphs, show that the equation `sqrtx= e^x-3` has only one root.
b) Show by calculation that this root lies between `1` and `2`.
c) Show that, if a sequence of values given by the iterative formula `x_(n+1)=ln (3+sqrtx_n)` converges, then it converges to the root of the equation in (a).
Easy
Mark as Complete
Mark Scheme
Question 2
a) By sketching a suitable pair of graphs, show that the equation `cot x =2-cos x` has one root in the interval `0≤x≤1/2pi`
b) Show by calculation that this root lies between `0.6` and `0.8`.
c) Use the iterative formula`x_(n+1)=(frac{1}{2-cos x_n} )` to determine the root correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
Hard
Mark as Complete
Mark Scheme
Question 3
The parametric equations of a curve are `x=ln (1-2t)`, `y=2/t`, for `t<0`
a) Show that `(dy)/dx=frac{1-2t}{t^2}`.
b) Find the exact coordinates of the only point on the curve at which the gradient is `3`.
Mark as Complete
Mark Scheme
Question 4
The equation of a curve is `x^2y+y^2=6x`
a) Show that `(dy)/dx=frac{6-2xy}{x^2+2y}`
b) Find the equation of the tangent to the curve at the point with coordinates `(1, 2)` , giving your answer in the form `ax+by+c=0`
Medium
Mark as Complete
Mark Scheme
Question 5
a) Use the trapezium rule with two intervals to estimate the value of `int_0^1 frac{1}{6+2e^x}dx`, giving your answer correct to `2` decimal places.
b) Find `intfrac{(ex-2)^2}{e^(2x)}dx`.
Medium
Mark as Complete
Mark Scheme
Question 6
a) By sketching a suitable pair of graphs, show that the equation`ln x =4-1/2x` has exactly one real root, `alpha`
b) Verify by calculation that `4.5<α<5.0`
c) Use an iterative formula `x_(n+1)=8-2ln x_n` to find `α` correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
Medium
Mark as Complete
Mark Scheme
Question 7
The parametric equations of a curve are `x=1/t`, `y=t`, where `0≤t≤1/2 pi`
a) Show that `(dy)/dx=sin t`
b) Hence show that the equation of the tangent to the curve at the point with parameter `t` is `y=xsin t -tan t`
Medium
Mark as Complete
Mark Scheme
Question 8
It is given that the positive constant a is such that `int_-a^a(4e^(2x)+5)dx=100`
a) Show that `a=1/2ln (50+e^(-2a)-5a)`
b) Use the iterative formula `a_(n+1)=1/2ln (50+e^(-2a_n)-5a_n)` to find `alpha` correct to `3` decimal places. Give the result of each iteration to `5` decimal places.
Medium
Mark as Complete
Mark Scheme
Question 9
a) Prove that `tan theta +cot theta -= frac{2}{sin 2θ}`
b) Hence find the exact value of `tan frac{1}{8}π+cotfrac{ 1}{8} pi`
c) Hence evaluate `int_0^(1/2pi)frac{6}{ tan theta +cot theta } d theta`
Medium
Mark as Complete
Mark Scheme
Question 10
The equation of a curve is `y=frac{3x^2}{x^2+4}`. At the point on the curve with positive x-coordinate p, the gradient of the curve is `1/2`
a) Show that `p=sqrt(frac{48_p-16}{p^2+8})`
b) Show by calculation that `2 < p < 3`
c) Use an iterative formula based on the equation in part (a) to find the value of `p` correct to `4` significant figures. Give the result of each iteration to `6` significant figures.
Medium
Mark as Complete
Mark Scheme
Question 11
a) By differentiating `frac{1}{cos theta '}` , show that if `y=sec theta`then `(dy)/(dθ)=tan theta sec theta`
b) Hence show that `(d^2y)/(d theta^2)=a theta +bsec theta` , giving the value of `a` and `b`
c) Find the exact value of `int_0^4(1+ theta -3tan theta sec theta )dθ`
Hard
Mark as Complete
Mark Scheme
Question 12
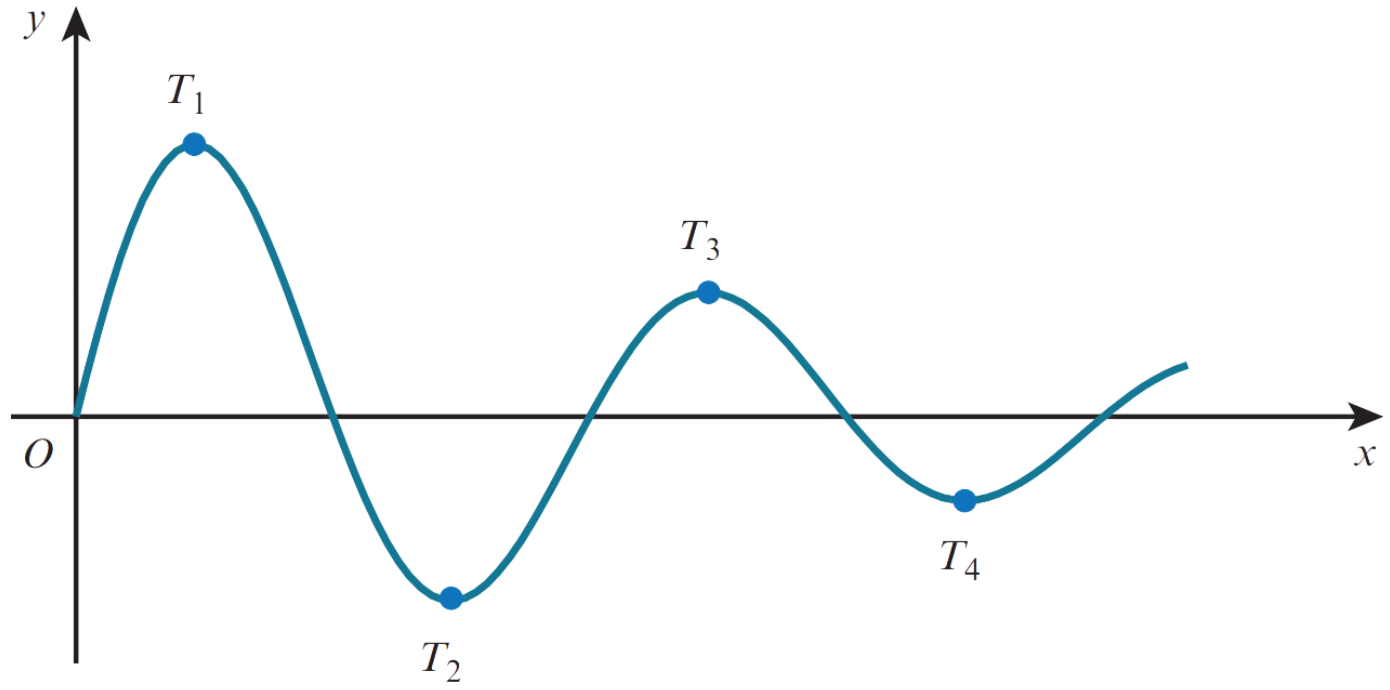
The diagram shows the curve `y=10e^(-1/2x) sin 4x` for `x≥0`. The stationary points are labeled `T_1, T_2, T_3`,… as shown.
a) Find the x-coordinate of `T_1` and `T_2'`, giving each x-coordinate correct to `3` decimal places.
b) It is given that the x-coordinate of `T_n` is greater than `25`. Find the least possible value of `n`.
Hard
Mark as Complete
Mark Scheme
Question 13
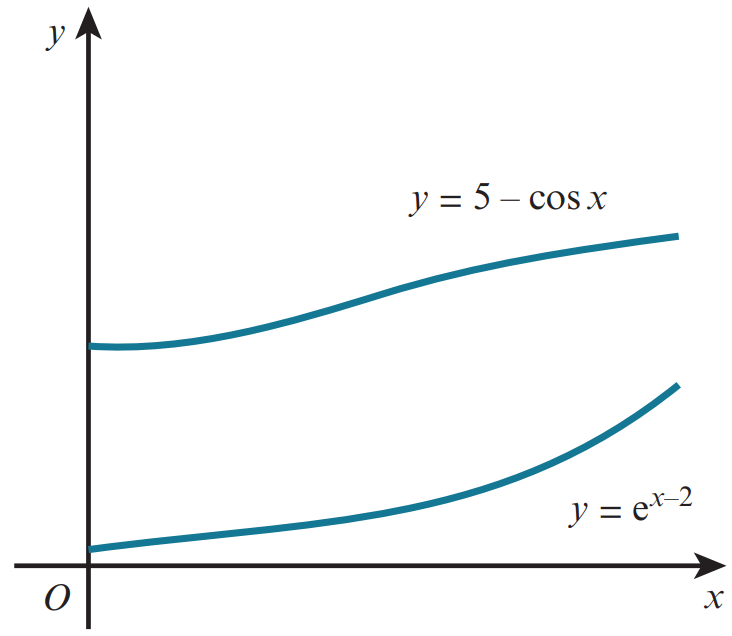
The function f and g are defined, for
`0, by `f(x)=e^(x-2 )`and `g(x)=5-cos x`.
The diagram shows the graph of `y=f(x)` and the graph `y=g(x)`.
The gradients of the curves are equal both when `x=p` and when `x=q`.
a) Given that `p < q`, verify by calculation that `p` is `0.16` correct to `2` decimal places.
b) Show that `q` satisfies the equation `q=2+ln sin q`.
c) Given also that `1.5 < q < 2.5`, use the iterative formula `q_(n+1)=2+ln sin q_n` to calculate `q` correct to `2` decimal places, showing the result of each iteration to `4` decimal places.
Medium
Mark as Complete
Mark Scheme
Question 14
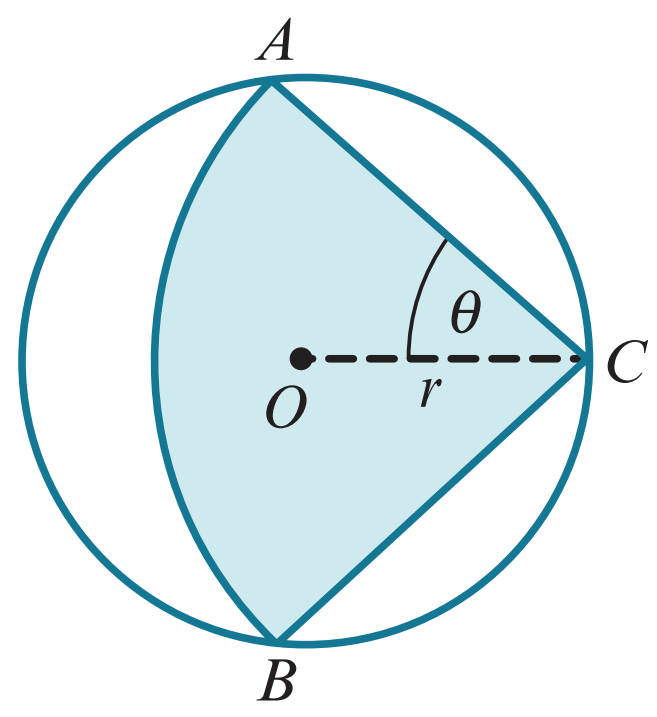
In the diagram, A, B and C are points on the circumference of the circle with centre O and radius `r`. The shaded region, ABC, is a sector of the circle with centre C. Angle OCA is equal to `θ` radians.
The area of the shaded region is equal to `3/8` of the area of the circle.
a) Show that `θ=sqrtfrac{3π}{32θ}`
b) Verify by calculation that lies between `0.8` and `1.2` radians.
c) Use the iterative formula `theta_ (n+1)=sqrtfrac{3pi}{32theta _n}` to find the value of `θ` correct to `3` decimal places. Give the result of each iteration to `5` decimal places.
Hard
Mark as Complete
Mark Scheme
Question 15
It is given that `int_0^a(frac{1}{3x+5}+2e^(6x))dx = 0.6`, where the constant `a>0`
a) Show that `a=1/6ln (2.8+ln(frac{ 5}{3a+5}))`
b) Use an iterative formula based on the equation in part a, with a starting value of `a=0.2`, to find the value of `a` correct to `3` decimal places. Give the result of each iteration to an appropriate number of decimal places.
Medium
Mark as Complete
Mark Scheme
Question 16
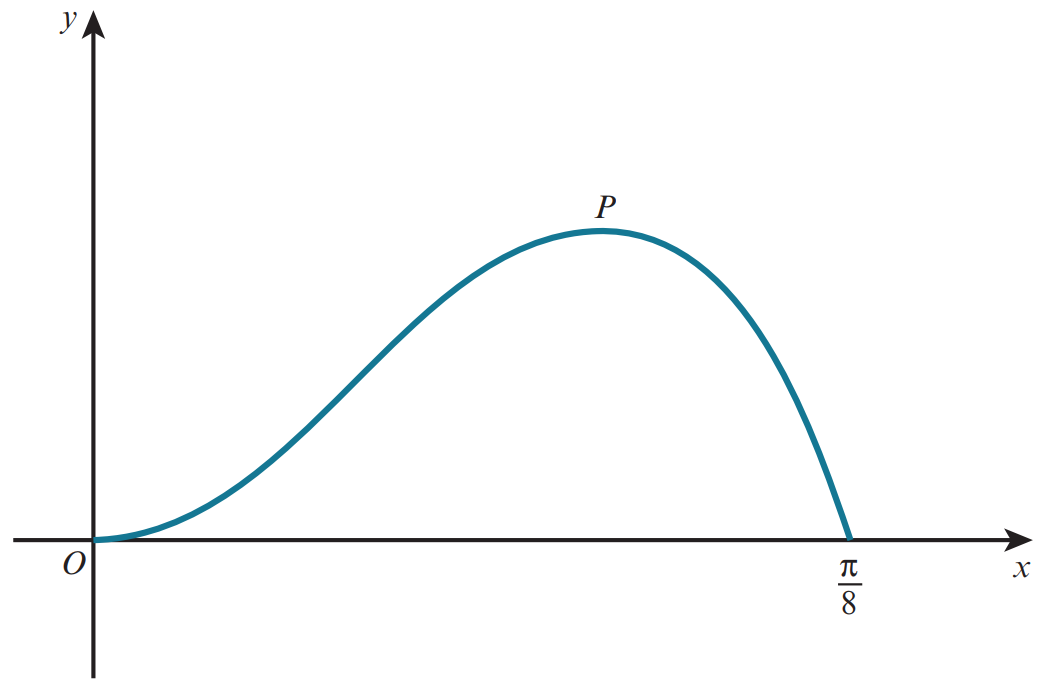
The diagram show the curve `y=x^2cos 4x` for `0≤x≤pi/8`. The point P is a maximum point.
a) Show that the x-coordinate of P satisfies the equation `4x^2tan 4x =2x`.
b) Show also that the x-coordinate of P satisfies the equation `x=1/4 1/(2x)`.
c) Using an iterative formula based on the equation in part b with initial value `x_1=0.3` find the x-coordinate of P correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
d) Use integration by parts twice to find the exact area enclosed between the curve and the x-axis from `0` to `pi/8`.
Hard
Mark as Complete
Mark Scheme
Question 17
a)
By sketching each of the graphs`y=x` and`y=x(π-x)` for `0, show that the equation `x = x(π-x)` has exactly two real roots in the interval for `0 < x < pi`.
b)
Show that the equation `x = x(π-x)` can be written in the form `x=frac{1+x^2sin x}{ pi sin x}`
c)
The two real roots of the equation `x = x(π-x)` in the interval `0 are denoted by `alpha` and `beta`, where `α<β`.
Use the iterative formula `x_(n+1)=frac{1+x_n^2sin x_n}{ pisin x_n}` to find `alpha` correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
Deduce the value of `beta` correct to `2` decimal places.
Medium
Mark as Complete
Mark Scheme
Question 18
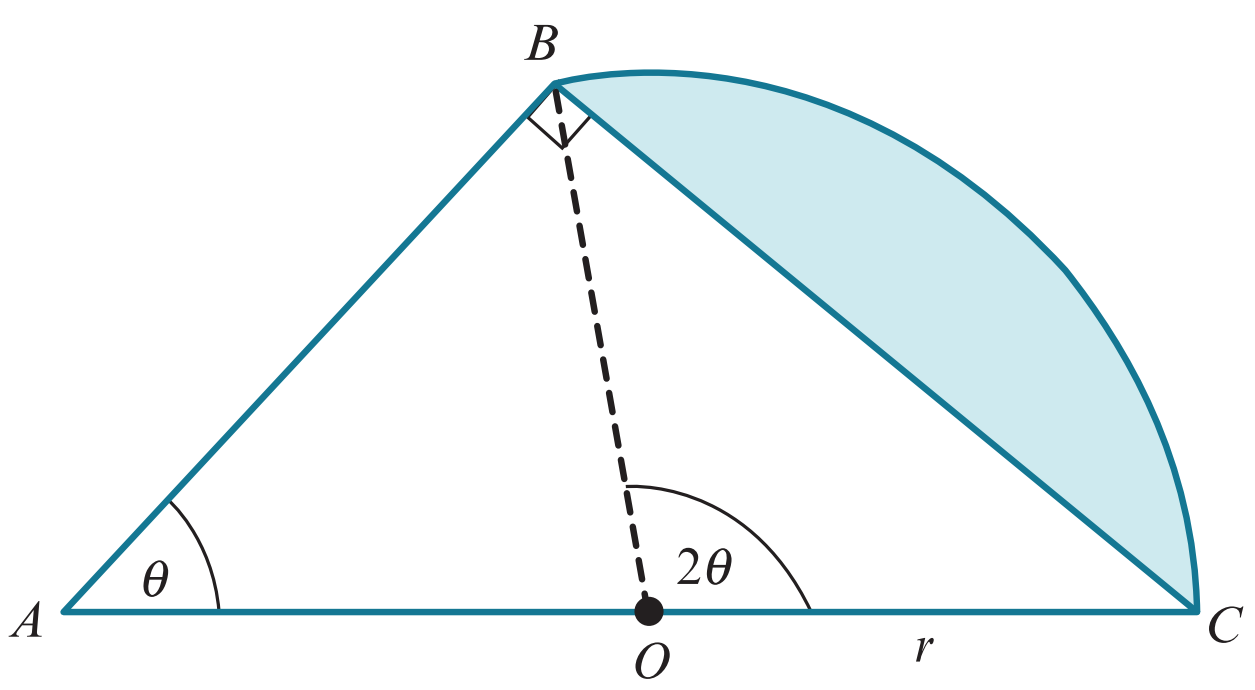
In the diagram, triangle ABC is right-angled and angle BAC is `theta` radians. The point O is the mid point of AC and OC `= r`. Angle BOC is `2theta` radians and BOC is a sector of the circle with centre O. The area of triangle ABC is 2 times the area of the shaded segment.
a) Show that satisfies the equation `sin 2θ =θ`
b)This equation has one root in the interval `0<θ. Use the iterative formula `theta _(n+1)=sin 2 theta_n` to determine the root correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
Hard
Mark as Complete
Mark Scheme
Question 19
The parametric equations of a curve are `x=t^2+6`, `y=t^4-t^3-5t`.
The curve has a stationary point for a value of t that lies between `1` and `2`.
a) Show that the value of t at this stationary point satisfies the equation `t=root(3)frac{3t^2+5}{4}`
b) Use an iterative process based on the equation in part a to find the value of `t` correct to `3` decimal places. Show the result of each iteration to `6` decimal places.
c) Hence find the coordinates of the stationary point, giving each coordinate correct to `1` significant figure.
Medium
Mark as Complete
Mark Scheme
Question 20
a) Show that `(frac{1+cos x}{ 2sin x})^ 2+ (frac{1-cos x}{ 2sin x})^ 2=x+1/2`
b) Hence, given that `alpha` is a root of the equation `(frac{1+cos x}{ 2sin x})^ 2+ (frac{1-cos x}{ 2sin x})^ 2=x`, show that `alpha` is also a root of the equation `x=sqrt((2)/(2x-1))` for `0 < x < pi/2`
c) It is given that `alpha` is the only root of the equation `x=sqrt((2)/(2x-1))` for `0 < x < pi/2`. Verify by calculation that the value of `alpha` lies between `0.9` and `1.0`.
Medium
Mark as Complete
Mark Scheme
Question 1
a) By sketching a suitable pair of graphs, show that the equation `sqrtx= e^x-3` has only one root.
b) Show by calculation that this root lies between `1` and `2`.
c) Show that, if a sequence of values given by the iterative formula `x_(n+1)=ln (3+sqrtx_n)` converges, then it converges to the root of the equation in (a).
a)
Sketch a relevant graph:
`y=e^x-3`should cut vertical axis at `(0, –2)` and have increasing gradient.
`y=sqrtx`should start at `(0, 0)` and have reducing grading
Ignore anything outside 1st and 4th quadrants.
b)
Calculate the values of a relevant expression or pair of expressions at `x = 1` and `x = 2`
Complete the argument correctly with correct calculated values: `1.28 > 0`, `-2.98 < 0`.
c)
State `x=ln (3+sqrtx)` and rearrange to the given equation `sqrtx=e^x-3`
Question 2
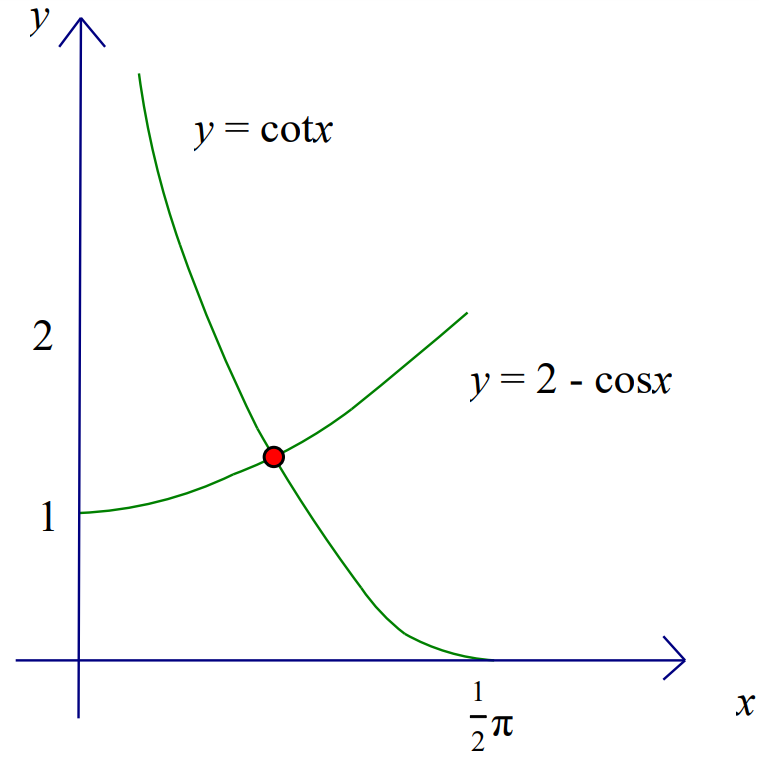
a) By sketching a suitable pair of graphs, show that the equation `cot x =2-cos x` has one root in the interval `0≤x≤1/2pi`
b) Show by calculation that this root lies between `0.6` and `0.8`.
c) Use the iterative formula`x_(n+1)=(frac{1}{2-cos x_n} )` to determine the root correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
a)
Sketch a relevant graph.
Ignore anything outside `0≤x≤1/2 pi`
b)
Calculate the value of a relevant expression or values of a pair of expressions at
`x=0.6`: `cot 0.6 > 2-cos 0.6 -> 1.46>1.17`
Calculate the value of a relevant expression or values of a pair of expressions at `x=0.8`: `cot 0.8 < 2-cos 0.8 -> 0.97<1.30`
Complete the argument correctly with correct calculated value
c)
Calculate the value of a relevant expression or values of a pair of expressions at `x=0.6` and `x=0.8` (Must be working in radians)
Show sufficient iterations to at least `4` d.p. to justify `0.68` to `2` d.p.
`x_1=0.6`
`x_2=(frac{1}{2-cos 0.6} ) =0.7054`
`x_3=(frac{1}{2-cos 0.7054} ) =0.6792`
`x_4=(frac{1}{2-cos 0.6792} ) =0.6858`
`x_5=(frac{1}{2-cos 0.6858 }) =0.6841`
Obtain final answer `0.68`
Question 3
The parametric equations of a curve are `x=ln (1-2t)`, `y=2/t`, for `t<0`
a) Show that `(dy)/dx=frac{1-2t}{t^2}`.
b) Find the exact coordinates of the only point on the curve at which the gradient is `3`.
a)
`y=2t^-1`
`frac{dy}{dt}=-2t-^2=(-2)/(t^2)`
`x=ln (1-2t)`
`(dx)/dt=frac{-2}{1-2t }`
`(dy)/dx=(dy)/dt.(dt)/dx=-2/(t^2) xx (1-2t)/-2=(1-2t)/t^2`
b)
When the gradient is 3, that means `(dy)/dx=3`
`frac{1-2t}{t^2}=3`
`1-2t=3t^2`
`(3t-1)(t+1)=0`
`t=13` or `t=-1`
But `t<0` so `t=-1`
`x=ln 3 -> y=-2`
So the coordinates of the only point on the curve at which the gradient is 3 are `(ln 3 , -2)`
Question 4
The equation of a curve is `x^2y+y^2=6x`
a) Show that `(dy)/dx=frac{6-2xy}{x^2+2y}`
b) Find the equation of the tangent to the curve at the point with coordinates `(1, 2)` , giving your answer in the form `ax+by+c=0`
a) Differentiating with respect to x, using the chain and product rule
`x^2y+y^2=6x`
`2xy+x^2(dy)/dx+2y(dy)/dx=6`
`(dy)/dx(x^2+2y)=6-2xy`
`(dy)/dx=frac{6-2xy}{x^2+2y}`
b)
At the point `(1, 2)`
`(dy)/dx=frac{6-2xy}{x^2+2y}=frac{6-2(1)(2)}{1^2+2(2)}=2/5`
Equation of tangent:
`y-2=2/5(x-1)`
`2x-5y+8=0`
Question 5
a) Use the trapezium rule with two intervals to estimate the value of `int_0^1 frac{1}{6+2e^x}dx`, giving your answer correct to `2` decimal places.
b) Find `intfrac{(ex-2)^2}{e^(2x)}dx`.
a) Set out your different ordinates carefully in a table, as shown here
`h=frac{1-0}{2}=1/2`

`int_0^1 frac{1}{6+2e^x}dx ~~h/2(y_0+y_2+2y_1)`
`=1/4 (frac{1}{6+2e^0}+frac{1}{6+2e^1}+frac{2}{6+2e^(0.5)}=0.11`
b)
`intfrac{(ex-2)^2}{e^(2x)}dx`
`=intfrac{e^(2x)-4e^x+4}{e^(2x)}dx`
`= int(1-4e^(-x)+4e^(-2x))dx`
`= x+4e^-x-2e^(-2x)+c`
Question 6
a) By sketching a suitable pair of graphs, show that the equation`ln x =4-1/2x` has exactly one real root, `alpha`
b) Verify by calculation that `4.5<α<5.0`
c) Use an iterative formula `x_(n+1)=8-2ln x_n` to find `α` correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
a) Sketching the graphs`y=ln x` and`y=4-1/2x`
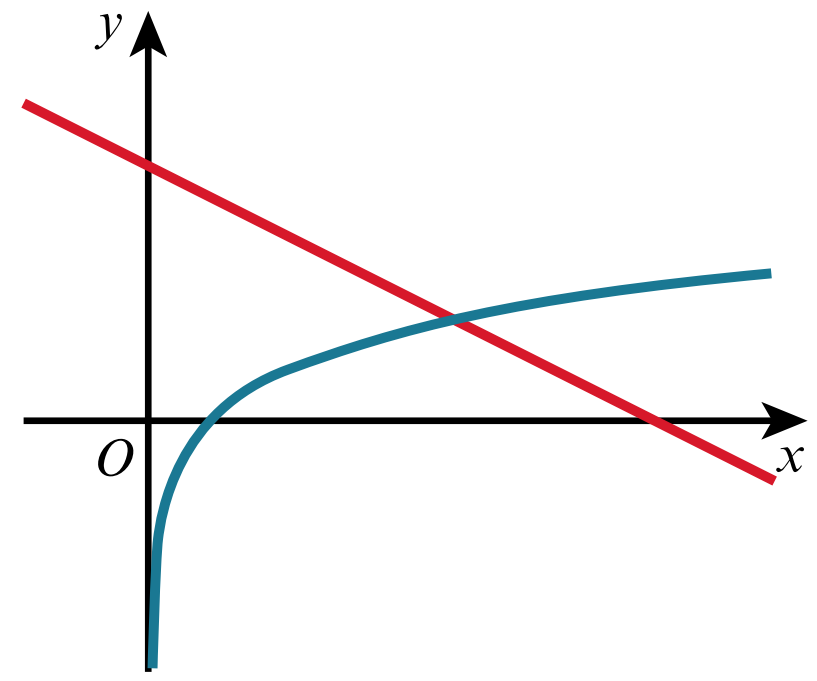
Note: here is only point of intersection, so the given equation has only one real root.
b) `f(x)=ln x -4+1/2x`
`f(4.5)=-0.2459<0`
`f(5)=0.1093>0`
Change of sign indicates the presence of a root between `4.5` and `5`
So, `4.5<α<5.0`
c) Using `x_(n+1)=8-2ln x_n`with `x_o=4.75`
`x_1=4.8837`
`x_2=4.8282`
`x_3=4.8511`
`x_4=4.8416`
`x_5=4.8455`
`x_6=4.8439`
`x_7=4.8446`
`x_8=4.8443`
`x_9=4.8444`
So, `α=4.84` (to `2` decimal places)
Question 7
The parametric equations of a curve are `x=1/t`, `y=t`, where `0≤t≤1/2 pi`
a) Show that `(dy)/dx=sin t`
b) Hence show that the equation of the tangent to the curve at the point with parameter `t` is `y=xsin t -tan t`
a)
`x=(cos t )^-3`
`(dx)/dt=-3(cos t)^ -4xx(-sint )=frac{ 3sin t}{cos^4 t}`
`y= tan^3t`
`(dy)/dt=3tan^2 t sec^2t`
`(dy)/dx=(dy)/dt xx (dt)/dx=3tan^2t sec^2t xx (frac{1}{3sin t}cos^4t)`
`=frac{tan^2t cos^2t}{ sin t}= frac{sin^2t cos^2t}{sintcos^2t} = sin t`
b)
Gradient `= sin t` at the point`(1/cos^3t , tan^3t )`
Equation of tangent:
`y-tan^3t =sin t (x-1/cos^3t )`
`y=xsin t +sin^3t/cos^3t -frac{sin t}{ cos^3t}`
`y= xsin t -tan t`
Question 8
It is given that the positive constant a is such that `int_-a^a(4e^(2x)+5)dx=100`
a) Show that `a=1/2ln (50+e^(-2a)-5a)`
b) Use the iterative formula `a_(n+1)=1/2ln (50+e^(-2a_n)-5a_n)` to find `alpha` correct to `3` decimal places. Give the result of each iteration to `5` decimal places.
a)
`int_-a^a(4e^(2x)+5)dx=100`
`[2e^(2x)+5x]_-a^a=100`
`2e^(2a)+5a-(2e^(-2a)-5a)=100`
`e^(2a)=50+e^(-2a)-5a`
`2a=ln (50+e^(-2a)-5a)`
`a=1/2ln (50+e^(-2a)-5a)`
b)
`f(a)=1/2ln (50+e^(-2a)-5a) -a`
`f(1)=0.90483>0`
`f(2)=-0.15533<0`
Change of sign indicates the presence of a root between `1` and `2`
So `1<α<2`
Using `a_(n+1)=1/2ln (50+e^(-2a_n)-5a_n)`with`x_0=1.5`
`x_1=1.87534`
`x_2=1.85264`
`x_3=1.85388`
`x_4=1.85379`
`x_5=1.85380`
`x_6=1.85380`
So,`α=1.854`
Question 9
a) Prove that `tan theta +cot theta -= frac{2}{sin 2θ}`
b) Hence find the exact value of `tan frac{1}{8}π+cotfrac{ 1}{8} pi`
c) Hence evaluate `int_0^(1/2pi)frac{6}{ tan theta +cot theta } d theta`
a)
`tan theta +cot theta = frac{sin theta }{costheta } +frac{cos theta}{ sin theta}`
`=frac{sin^2θ+cos^2 theta}{sin theta cos theta } =frac{1}{sin theta cos theta}`
`=frac{2}{2sin theta cos theta } =frac{2}{sin 2θ }`
b)
Using the result from part (a)
tan 18π+cot 18 =2sin (2. 18π)
`=frac{2}{sinfrac{pi}{4}}= 2/(1/sqrt2)=2sqrt2`
c)
`int_0^(1/2)frac{6}{ tan theta +cot theta} dθ= int_0^(1/2pi)6(frac{sin 2θ}{ 2})dθ`
`=int_0^(1/2pi)3sin 2θ dθ=[-3/2cos 2θ]_0^(pi/2)`
`=-3/2cos pi +3/2cos 0 =3/2+3/2=3`
Question 10
The equation of a curve is `y=frac{3x^2}{x^2+4}`. At the point on the curve with positive x-coordinate p, the gradient of the curve is `1/2`
a) Show that `p=sqrt(frac{48_p-16}{p^2+8})`
b) Show by calculation that `2 < p < 3`
c) Use an iterative formula based on the equation in part (a) to find the value of `p` correct to `4` significant figures. Give the result of each iteration to `6` significant figures.
a)
`y=frac{3x^2}{x^2+4 }`
Using the quotient rule
`(dy)/dx=frac{(x^2+4)(6x)-3x^2(2x)}{(x^2+4)^2 }`
`=frac{24x}{(x^2+4)^2}`
Using the fact that the gradient is `1/2` at `x=p`
`frac{24p}{(p^2+4)^2}=1/2`
`48p=(p^2+4)^2`
`p^4+8p^2-48p+16=0`
`p^2(p^2+8)=48p-16`
`p^2=frac{48p-16}{p^2+8 }`
`p=sqrt(frac{48p-16}{p^2+8} )`
b)
`f(p)=sqrt(frac{48p-16}{p^2+8})-p`
`f(2)=0.582>0`
`f(3)=-0.256<0`
Change of sign indicates the presence of a root between `2` and `3`
So `2 < p < 3`
c)
Using `p_(n+1)=sqrt(frac{48p_n-16}{p_n^2+8})` with `p_0=2.5`
`p_1=2.70153`
`p_2=2.72589`
`p_3=2.72811`
`p_4=2.72831`
`p_5=2.72832`
`p_6=2.72833`
`p=2.728`
Question 11
a) By differentiating `frac{1}{cos theta '}` , show that if `y=sec theta`then `(dy)/(dθ)=tan theta sec theta`
b) Hence show that `(d^2y)/(d theta^2)=a theta +bsec theta` , giving the value of `a` and `b`
c) Find the exact value of `int_0^4(1+ theta -3tan theta sec theta )dθ`
a)
`y=sec theta =frac{1}{cos theta} = theta`
`(dy)/(dθ)=- theta xx -sin theta =frac{sin theta}{theta}`
`=frac{sin theta }{cos theta } xx frac{1}{cos theta }=tan theta sectheta`
b)
`(d^2y)/(d theta ^2)=d/(d theta )(tan theta sec theta )`
`= theta "sec" theta +tan theta tan theta sec theta`
`= theta + theta sectheta`
`= theta + theta -1) sec theta`
`= theta + theta -sec theta`
`=2 theta -sec theta`
So `a=2` and `b=-1`
c)
`1+ theta = theta`
`int_0^(pi/4)(1+ theta -3tan theta sec theta)dθ`
`int_0^(pi/4)(theta -3tan theta sec theta )dθ`
`=[tan theta -3sec theta ]_0^(pi/4)`
`=tan frac{pi}{4}-frac{3}{cos frac{pi}{4}} -0+ frac{3}{cos 0 }`
`=1-frac{3}{1/sqrt2}+3`
`=4-3sqrt2`
Question 12

The diagram shows the curve `y=10e^(-1/2x) sin 4x` for `x≥0`. The stationary points are labeled `T_1, T_2, T_3`,… as shown.
a) Find the x-coordinate of `T_1` and `T_2'`, giving each x-coordinate correct to `3` decimal places.
b) It is given that the x-coordinate of `T_n` is greater than `25`. Find the least possible value of `n`.
a)
`(dy)/dx=-5e^(-1/2x)sin 4x +40e^(-1/2x)cos 4x`
`=5e^(-1/2x)(8cos 4x -sin 4x )`
`e^(-1/2x)>0`
At all T:
`8cos 4x -sin 4x =0`
`8cos 4x =sin 4x`
`tan 4x =8`
`4x=1.44644133+(n+1)π`, where `n=1, 2, 3, 4,…`
`x=frac{1.44644133+(n+1)π}{4}`
`T_1` and `T_2` occur at the two smallest values, with `n=1` and `2`
`x=0.362, 1.147`
b)
`frac{1.44644133+(n+1)π}{4}>25`
`1.44644133+(n+1)π >100`
`(n+1)π>100-1.44644133`
`n+1>frac{100-1.44644133}{pi}`
`n>32.4`
Smallest `n` satisfying this inequality is `33`
Question 13

The function f and g are defined, for
`0, by `f(x)=e^(x-2 )`and `g(x)=5-cos x`.
The diagram shows the graph of `y=f(x)` and the graph `y=g(x)`.
The gradients of the curves are equal both when `x=p` and when `x=q`.
a) Given that `p < q`, verify by calculation that `p` is `0.16` correct to `2` decimal places.
b) Show that `q` satisfies the equation `q=2+ln sin q`.
c) Given also that `1.5 < q < 2.5`, use the iterative formula `q_(n+1)=2+ln sin q_n` to calculate `q` correct to `2` decimal places, showing the result of each iteration to `4` decimal places.
a)
`f'(x)=e^(x-2)`
`g'x=sin x`
Letting `h(x)=f'(x)-g'(x)`
`h(x)=e^(x-2)-sin x`
When `x=p`, `h(p)=0`
`h(0.155)=0.00364>0`
`h(0.165)=-0.00463<0`
Change of sign indicates the presence of a root between `0.155` and `0.165`, which means that the root is `0.16` to `2` decimal places.
b)
`f'(x)=g'(x)`
`e^(q-)2=sin q`
`q-2=ln sin q`
`q=2+ln sin q`
c)
Using `q_(n+1)=2+ln (sin q_n)` with `q_1=2`
`q_2=1.9049`
`q_3=1.9431`
`q_4=1.9290`
`q_5=1.9344`
`q_6=1.9324`
So `q=1.93` to `2` decimal places.
Question 14

In the diagram, A, B and C are points on the circumference of the circle with centre O and radius `r`. The shaded region, ABC, is a sector of the circle with centre C. Angle OCA is equal to `θ` radians.
The area of the shaded region is equal to `3/8` of the area of the circle.
a) Show that `θ=sqrtfrac{3π}{32θ}`
b) Verify by calculation that lies between `0.8` and `1.2` radians.
c) Use the iterative formula `theta_ (n+1)=sqrtfrac{3pi}{32theta _n}` to find the value of `θ` correct to `3` decimal places. Give the result of each iteration to `5` decimal places.
a)
Using the sin rule:
Remember that `sin (π-θ) =sin theta` . This is because the graph of `y=sin theta` has a line of symmetry at `θ= pi/2`
`frac{r}{sin theta} =frac{a}{sin (π-2θ)}`
`frac{r}{sin theta }=frac{a}{sin (pi - 2θ)}`
`rsin (2θ) =asin theta`
`2rsin theta cos theta = theta`
`a=2rcos theta`
Using the fact that the area of the shaded region is equal to `3/8`of the area of the circle:
`frac{1/2a^2(2θ)}{r^2}=3/8`
`frac{8r^2 theta theta}{ 2πr^2}=3/8`
`theta =frac{3pi}{32θ}`
`cos theta =sqrtfrac{3π}{32θ }`
`θ=sqrtfrac{3π}{32θ}`
b)
`f(theta)=θ-sqrtfrac{3π}{32θ}`
`f(0.8)= 0.8-sqrtfrac{3π}{25.6} <0`
`f(1.2)= 1.2-sqrtfrac{3π}{38.4} >0`
Change of sign indicates that lies between `0.8` and `1.2`
c)
Using `theta _(n+1)=sqrtfrac{3π}{32_n}` with `theta_1=1`
`theta_2= 0.99715`
`theta_3= 0.99622`
`theta_4= 0.99592`
`theta_5= 0.99582`
`theta_6= 0.99579`
So `θ=0.996` to `3` decimal places.
Question 15
It is given that `int_0^a(frac{1}{3x+5}+2e^(6x))dx = 0.6`, where the constant `a>0`
a) Show that `a=1/6ln (2.8+ln(frac{ 5}{3a+5}))`
b) Use an iterative formula based on the equation in part a, with a starting value of `a=0.2`, to find the value of `a` correct to `3` decimal places. Give the result of each iteration to an appropriate number of decimal places.
a)
`int_0^a(1/(3x+5)+2e^(6x))dx = 0.6`
`[1/3ln( 3x+5)+1/3e^(6x) ]_0^a=0.6`
`1/3ln( 3a+5)+1/3e^(6a)-1/3ln 5 -1/3=0.6`
`e^(6a)=1+1.8+ln 5 -ln (3a+5)`
`6a=ln [2.8+ln( 3a+5)]`
`a=1/6ln( 2.8+ln (5/(3a+5)))`
b)
Using `a_(n+1)=1/6ln (2.8+ln( 5/(3a_n+5)))` with `a_1=0.2`
`a_2=0.164717`
`a_3=0.165897`
`a_4=0.165857`
`a_5=0.165858`
So `a=0.166` to `3` decimal places
Question 16

The diagram show the curve `y=x^2cos 4x` for `0≤x≤pi/8`. The point P is a maximum point.
a) Show that the x-coordinate of P satisfies the equation `4x^2tan 4x =2x`.
b) Show also that the x-coordinate of P satisfies the equation `x=1/4 1/(2x)`.
c) Using an iterative formula based on the equation in part b with initial value `x_1=0.3` find the x-coordinate of P correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
d) Use integration by parts twice to find the exact area enclosed between the curve and the x-axis from `0` to `pi/8`.
a)
`y=x^2cos 4x`
`(dy)/dx=2xcos 4x -4x^2sin 4x`
At point P, `(dy)/dx=0`
`2xcos 4x -4x^2sin 4x =0`
`4x^2sin 4x =2xcos 4x`
`frac{4x^2sin 4x }{cos 4x} =2x`
`4x^2tan 4x =2x`.
b)
`4x^2tan 4x =2x`
`tan 4x =frac{2x}{4x^2}`
`4x=1/(2x)`
`x=1/4 1/(2x)`.
c)
Using `x_(n+1)=1/4 1/(2x_n)` with `x_1=0.3`
`x_2=0.2576`
`x_3=0.2738`
`x_4=0.2675`
`x_5=0.2699`
`x_6=0.2690`
So the x-coordinate of P is `0.27` to `2` decimal places.
d)
`int_0^(pi/8)x^2cos 4x dx`
`=[x^2(1/4sin 4x)] _0^(pi/8)-int_0^(pi/8)(1/4 (2x)sin 4x) dx`
`=1/4 (pi/8)^2sinfrac{pi}{2} -0-1/2{int_0^(pi/8)xsin 4x dx}`
`=frac{pi^2}{256}-1/2{[-1/4xcos 4x]_ 0^(pi/8)-int_0^(pi/8)(-1/4cos 4x) dx}`
`=frac{pi^2}{256}-1/2(0-0)-1/8 int_0^(pi/8)cos 4x dx`
`=frac{pi^2}{256}-1/8 [1/4sin 4x]_ 0^(pi/8)`
`=frac{pi^2}{256}-1/32`
Question 17
a)
By sketching each of the graphs`y=x` and`y=x(π-x)` for `0, show that the equation `x = x(π-x)` has exactly two real roots in the interval for `0 < x < pi`.
b)
Show that the equation `x = x(π-x)` can be written in the form `x=frac{1+x^2sin x}{ pi sin x}`
c)
The two real roots of the equation `x = x(π-x)` in the interval `0 are denoted by `alpha` and `beta`, where `α<β`.
Use the iterative formula `x_(n+1)=frac{1+x_n^2sin x_n}{ pisin x_n}` to find `alpha` correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
Deduce the value of `beta` correct to `2` decimal places.
a)
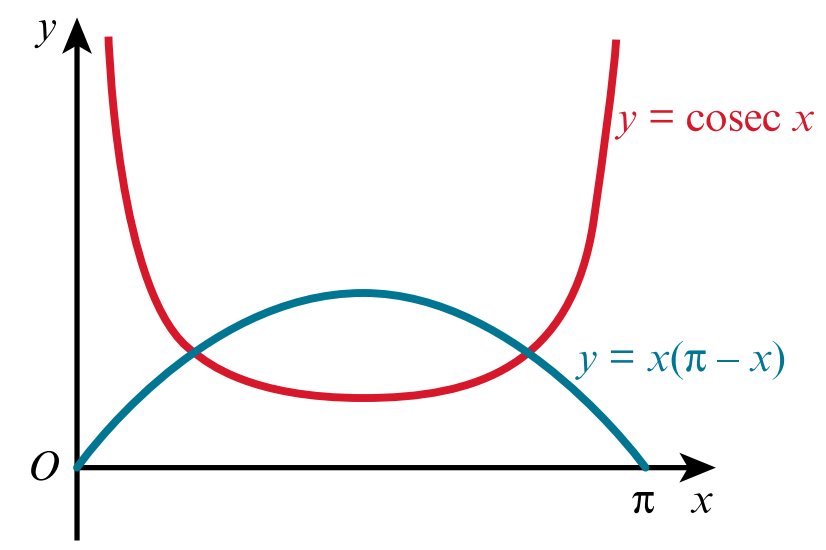
Note that the graphs intersect twice, so the given equation has two real roots in the given interval.
b)
`x = x(π-x)`
`frac{1}{sin x} = x(π-x)`
`1=xπsin x -x^2sin x`
`1+x^2sin x =xπsin x`
`x=frac{1+x^2sin x}{pi sin x}`
c)
i.
`alpha` is the smallest root and can be seen, from part a, to lie between `0` and `pi/2`.
Using `x_(n+1)=frac{1+x_n^2sin x_n}{ sin x_n }`with `x_0=1`
`x_1= 0.6966`
`x_2= 0.6506`
`x_3= 0.6603`
`x_4= 0.6577`
`x_5= 0.6584`
`α=0.66` to `2` decimal places.
ii.
Note that `sin (π-x) =sin x` by symmetry
Similary, `x(π-x)` has the same value if `x` is replaced by `π-x`
`β=π-α=2.48`to `2` decimal places.
Question 18

In the diagram, triangle ABC is right-angled and angle BAC is `theta` radians. The point O is the mid point of AC and OC `= r`. Angle BOC is `2theta` radians and BOC is a sector of the circle with centre O. The area of triangle ABC is 2 times the area of the shaded segment.
a) Show that satisfies the equation `sin 2θ =θ`
b)This equation has one root in the interval `0<θ. Use the iterative formula `theta _(n+1)=sin 2 theta_n` to determine the root correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
a)
Shaded segment area `= 1/2r^2 (2θ)-1/2r^2 sin 2θ =r^2 θ-1/2r^2sin 2θ`
`AB=2rcos theta`
Area of triangle `= 1/2 (2rcostheta xx 2rsin theta) =2r^2sin theta cos theta`
Using the fact that the area of the triangle is 2 times the area of the shaded segment:
`2r^2sin theta cos theta =2(r^2θ-1/2r^2sin 2θ )`
`r^2sin theta =2r^2θ-r^2sin 2θ`
`2r^2sin 2 theta =2r^2 theta`
`sin 2θ = theta`
b)
Using `theta_(n+1)=sin 2theta_1` with `theta_1=pi/4`
`theta_2=1`
`theta_3=0.9093`
`theta_4=0.9695`
`theta_5=0.9330`
`theta_6=0.9567`
So the root has the value of `0.95` to `2` decimal places.
Question 19
The parametric equations of a curve are `x=t^2+6`, `y=t^4-t^3-5t`.
The curve has a stationary point for a value of t that lies between `1` and `2`.
a) Show that the value of t at this stationary point satisfies the equation `t=root(3)frac{3t^2+5}{4}`
b) Use an iterative process based on the equation in part a to find the value of `t` correct to `3` decimal places. Show the result of each iteration to `6` decimal places.
c) Hence find the coordinates of the stationary point, giving each coordinate correct to `1` significant figure.
a)
`x=t^2+6`
`(dx)/dt=2t`[1]
`y=t^4-t^3-5t`
`(dy)/dt=4t^3-3t^2-5`
At the stationary point, `(dy)/dx=0`
`4t^3-3t^2-5=0`
`4t^3=5+3t^2`
`t^3=frac{5+3t^2}{4 }`
`t=root(3)frac{3t^2+5}{4}`
b)
Using `t_(n+1)=root3frac{3t_n^2+5}{4}` with `t_1=1.5`
`t_2= 1.432164`
`t_3= 1.407497`
`t_4= 1.398602`
`t_5= 1.395404`
`t_6= 1.394256`
`t_7= 1.393844`
So `t=1.394`to `3` decimal places.
c)
At the stationary point, `t=1.394`
`x=t^2+6=7.94`
`x=8` to `1` significant figure
`y=t^4-t^3-5t=-5.903`
`y=-6` to `1` significant figure
The point is `(8; -6)` to `1` significant figure.
Question 20
a) Show that `(frac{1+cos x}{ 2sin x})^ 2+ (frac{1-cos x}{ 2sin x})^ 2=x+1/2`
b) Hence, given that `alpha` is a root of the equation `(frac{1+cos x}{ 2sin x})^ 2+ (frac{1-cos x}{ 2sin x})^ 2=x`, show that `alpha` is also a root of the equation `x=sqrt((2)/(2x-1))` for `0 < x < pi/2`
c) It is given that `alpha` is the only root of the equation `x=sqrt((2)/(2x-1))` for `0 < x < pi/2`. Verify by calculation that the value of `alpha` lies between `0.9` and `1.0`.
a)
`(frac{1+cos x}{ 2sin x})^ 2+ (frac{1-cos x}{ 2sin x})^ 2`
`=frac{1+2cos x+x} {4x }+frac{1-2cos x +x}{ 4x}`
`=(2+2x)/( 4x)`
`=(1+1x)/( 2x)`
`=1/(2x) +x/( 2x)`
`=x/ 2+x/ 2`
`=(1+x )/2+x/ 2`
`=x +1/x`
b)
`x +1/x=x`
`x =x-1/x`
`cot x =sqrt(x-1/x )`
`1/tan x =sqrt((2x-1)/2)`
`tan x =sqrt(2/(2x-1))`
`x=sqrt(2/(2x-1))`
c)
Let `f(x)=x-sqrt(2/(2x-1))` and so `f(x)=0`, then
`f(0.9)=-0.10685<0`
`f(1)=0.44683>0`
Change of sign indicates the presence of a root.
Question 1
a) By sketching a suitable pair of graphs, show that the equation `sqrtx= e^x-3` has only one root.
b) Show by calculation that this root lies between `1` and `2`.
c) Show that, if a sequence of values given by the iterative formula `x_(n+1)=ln (3+sqrtx_n)` converges, then it converges to the root of the equation in (a).
Question 2
a) By sketching a suitable pair of graphs, show that the equation `cot x =2-cos x` has one root in the interval `0≤x≤1/2pi`
b) Show by calculation that this root lies between `0.6` and `0.8`.
c) Use the iterative formula`x_(n+1)=(frac{1}{2-cos x_n} )` to determine the root correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
Question 3
The parametric equations of a curve are `x=ln (1-2t)`, `y=2/t`, for `t<0`
a) Show that `(dy)/dx=frac{1-2t}{t^2}`.
b) Find the exact coordinates of the only point on the curve at which the gradient is `3`.
Question 4
The equation of a curve is `x^2y+y^2=6x`
a) Show that `(dy)/dx=frac{6-2xy}{x^2+2y}`
b) Find the equation of the tangent to the curve at the point with coordinates `(1, 2)` , giving your answer in the form `ax+by+c=0`
Question 5
a) Use the trapezium rule with two intervals to estimate the value of `int_0^1 frac{1}{6+2e^x}dx`, giving your answer correct to `2` decimal places.
b) Find `intfrac{(ex-2)^2}{e^(2x)}dx`.
Question 6
a) By sketching a suitable pair of graphs, show that the equation`ln x =4-1/2x` has exactly one real root, `alpha`
b) Verify by calculation that `4.5<α<5.0`
c) Use an iterative formula `x_(n+1)=8-2ln x_n` to find `α` correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
Question 7
The parametric equations of a curve are `x=1/t`, `y=t`, where `0≤t≤1/2 pi`
a) Show that `(dy)/dx=sin t`
b) Hence show that the equation of the tangent to the curve at the point with parameter `t` is `y=xsin t -tan t`
Question 8
It is given that the positive constant a is such that `int_-a^a(4e^(2x)+5)dx=100`
a) Show that `a=1/2ln (50+e^(-2a)-5a)`
b) Use the iterative formula `a_(n+1)=1/2ln (50+e^(-2a_n)-5a_n)` to find `alpha` correct to `3` decimal places. Give the result of each iteration to `5` decimal places.
Question 9
a) Prove that `tan theta +cot theta -= frac{2}{sin 2θ}`
b) Hence find the exact value of `tan frac{1}{8}π+cotfrac{ 1}{8} pi`
c) Hence evaluate `int_0^(1/2pi)frac{6}{ tan theta +cot theta } d theta`
Question 10
The equation of a curve is `y=frac{3x^2}{x^2+4}`. At the point on the curve with positive x-coordinate p, the gradient of the curve is `1/2`
a) Show that `p=sqrt(frac{48_p-16}{p^2+8})`
b) Show by calculation that `2 < p < 3`
c) Use an iterative formula based on the equation in part (a) to find the value of `p` correct to `4` significant figures. Give the result of each iteration to `6` significant figures.
Question 11
a) By differentiating `frac{1}{cos theta '}` , show that if `y=sec theta`then `(dy)/(dθ)=tan theta sec theta`
b) Hence show that `(d^2y)/(d theta^2)=a theta +bsec theta` , giving the value of `a` and `b`
c) Find the exact value of `int_0^4(1+ theta -3tan theta sec theta )dθ`
Question 12

The diagram shows the curve `y=10e^(-1/2x) sin 4x` for `x≥0`. The stationary points are labeled `T_1, T_2, T_3`,… as shown.
a) Find the x-coordinate of `T_1` and `T_2'`, giving each x-coordinate correct to `3` decimal places.
b) It is given that the x-coordinate of `T_n` is greater than `25`. Find the least possible value of `n`.
Question 13

The function f and g are defined, for
`0, by `f(x)=e^(x-2 )`and `g(x)=5-cos x`.
The diagram shows the graph of `y=f(x)` and the graph `y=g(x)`.
The gradients of the curves are equal both when `x=p` and when `x=q`.
a) Given that `p < q`, verify by calculation that `p` is `0.16` correct to `2` decimal places.
b) Show that `q` satisfies the equation `q=2+ln sin q`.
c) Given also that `1.5 < q < 2.5`, use the iterative formula `q_(n+1)=2+ln sin q_n` to calculate `q` correct to `2` decimal places, showing the result of each iteration to `4` decimal places.
Question 14

In the diagram, A, B and C are points on the circumference of the circle with centre O and radius `r`. The shaded region, ABC, is a sector of the circle with centre C. Angle OCA is equal to `θ` radians.
The area of the shaded region is equal to `3/8` of the area of the circle.
a) Show that `θ=sqrtfrac{3π}{32θ}`
b) Verify by calculation that lies between `0.8` and `1.2` radians.
c) Use the iterative formula `theta_ (n+1)=sqrtfrac{3pi}{32theta _n}` to find the value of `θ` correct to `3` decimal places. Give the result of each iteration to `5` decimal places.
Question 15
It is given that `int_0^a(frac{1}{3x+5}+2e^(6x))dx = 0.6`, where the constant `a>0`
a) Show that `a=1/6ln (2.8+ln(frac{ 5}{3a+5}))`
b) Use an iterative formula based on the equation in part a, with a starting value of `a=0.2`, to find the value of `a` correct to `3` decimal places. Give the result of each iteration to an appropriate number of decimal places.
Question 16

The diagram show the curve `y=x^2cos 4x` for `0≤x≤pi/8`. The point P is a maximum point.
a) Show that the x-coordinate of P satisfies the equation `4x^2tan 4x =2x`.
b) Show also that the x-coordinate of P satisfies the equation `x=1/4 1/(2x)`.
c) Using an iterative formula based on the equation in part b with initial value `x_1=0.3` find the x-coordinate of P correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
d) Use integration by parts twice to find the exact area enclosed between the curve and the x-axis from `0` to `pi/8`.
Question 17
a)
By sketching each of the graphs`y=x` and`y=x(π-x)` for `0, show that the equation `x = x(π-x)` has exactly two real roots in the interval for `0 < x < pi`.
b)
Show that the equation `x = x(π-x)` can be written in the form `x=frac{1+x^2sin x}{ pi sin x}`
c)
The two real roots of the equation `x = x(π-x)` in the interval `0 are denoted by `alpha` and `beta`, where `α<β`.
Use the iterative formula `x_(n+1)=frac{1+x_n^2sin x_n}{ pisin x_n}` to find `alpha` correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
Deduce the value of `beta` correct to `2` decimal places.
Question 18

In the diagram, triangle ABC is right-angled and angle BAC is `theta` radians. The point O is the mid point of AC and OC `= r`. Angle BOC is `2theta` radians and BOC is a sector of the circle with centre O. The area of triangle ABC is 2 times the area of the shaded segment.
a) Show that satisfies the equation `sin 2θ =θ`
b)This equation has one root in the interval `0<θ. Use the iterative formula `theta _(n+1)=sin 2 theta_n` to determine the root correct to `2` decimal places. Give the result of each iteration to `4` decimal places.
Question 19
The parametric equations of a curve are `x=t^2+6`, `y=t^4-t^3-5t`.
The curve has a stationary point for a value of t that lies between `1` and `2`.
a) Show that the value of t at this stationary point satisfies the equation `t=root(3)frac{3t^2+5}{4}`
b) Use an iterative process based on the equation in part a to find the value of `t` correct to `3` decimal places. Show the result of each iteration to `6` decimal places.
c) Hence find the coordinates of the stationary point, giving each coordinate correct to `1` significant figure.
Question 20
a) Show that `(frac{1+cos x}{ 2sin x})^ 2+ (frac{1-cos x}{ 2sin x})^ 2=x+1/2`
b) Hence, given that `alpha` is a root of the equation `(frac{1+cos x}{ 2sin x})^ 2+ (frac{1-cos x}{ 2sin x})^ 2=x`, show that `alpha` is also a root of the equation `x=sqrt((2)/(2x-1))` for `0 < x < pi/2`
c) It is given that `alpha` is the only root of the equation `x=sqrt((2)/(2x-1))` for `0 < x < pi/2`. Verify by calculation that the value of `alpha` lies between `0.9` and `1.0`.