Question 1
Let `f(x)=frac{24x+13}{(1-2x)(2+x)^2}`
(a) Express `f(x)` in partial fractions.
(b) Hence obtain the expansion of `f(x)` in ascending powers of `x`, up to and including the term in `x^2`.
Hard
Mark as Complete
Mark Scheme
Question 2
Let`f(x)=frac{17x^2-7x+16}{(2+3x^2)(2-x)}`
(a) Express `f(x)` in partial fractions
(b) Hence obtain the expansion of `f(x)`in ascending powers of `x`, up to and including the term in `x^3`
(c) State the set of values of `x` for which the expansion in (b) is valid. Give your answer in an exact form.
Hard
Mark as Complete
Mark Scheme
Question 3
Given that `frac{x^3+x^2-7}{x-3}=Ax^2+Bx+C+D/(x-3)`, find the values of A, B, C and D.
Medium
Mark as Complete
Mark Scheme
Question 4
Given that `(2x^4+3x^3+4x^2+5x+6)/(x^3+2x)=Ax+B+(Cx+D)/(x^3+2x)`, find the values of A, B, C and D.
Medium
Mark as Complete
Mark Scheme
Question 5
(a) Express `2/(x(x+2)` in partial fraction.
(b) Find an expression for the sum of the first `n` terms of the series.
`2/((1)xx(3))+2/((2)xx(4))+2/((3)xx(5))+2/((4)xx(6))+2/((5)xx(7))+…`
(c) Find the sum to infinity of this series.
Hard
Mark as Complete
Mark Scheme
Question 6
Given that `(1-3x)^-4-(1+2x)^(3/2)≈9x+kx^2` for small values of `x`, find the value of the constant.
Medium
Mark as Complete
Mark Scheme
Question 7
Given that `a/(1-x)+b/(1+2x)≈-3+12x` for small values of `x`, find the value of `a` and the value of `b`.
Medium
Mark as Complete
Mark Scheme
Question 8
When `(1+ax)^-3`, where a is a positive constant, is expanded the coefficients of x and `x^2` are equal.
(a) Find the value of `a`.
(b) When `a` has this value, obtain the first `5` terms in the expansion.
Medium
Mark as Complete
Mark Scheme
Question 9
When `(3-2x)(1+ax)^(2/3)` is expanded the coefficient of `x^2` is `-15`. Find the two possible values of `a`.
Medium
Mark as Complete
Mark Scheme
Question 10
The first `3` terms in the expansion of
`(1+ax)^n`are `1-24x+384x^2`.
(a) Find the value of `a` and the value of `n`.
(b) Hence find the term in `x^3`.
Hard
Mark as Complete
Mark Scheme
Question 11
In the expansion of `sqrt(3+ax )` where `a≠0`, the coefficient of the term in `x^2` is `3` times the coefficient of the term in `x^3`. Find the value of `a`.
Medium
Mark as Complete
Mark Scheme
Question 12
(a) Find the first `4` terms in the expansion of `(1+2/x)^-1`, where `|2/x|<1`.
(b) Show that`(1+2/x)^-1=x/(x+2)=x/2(1+x/2)^-1`.
Medium
Mark as Complete
Mark Scheme
Question 13
(a) Find the first `4` terms in the expansion of `x/2(1+x/2)^-1`, where `|x/2|<1`.
(b) Explain why your expansion are diffferent from the above question: `(1+2/x)^-1=x/(x+2)=x/2(1+x/2)^-1`.
Medium
Mark as Complete
Mark Scheme
Question 14
Expand `root(3)(1-6x)` in ascending powers of `x` up to and including the term in `x^3`, simplifying the coefficients.
Medium
Mark as Complete
Mark Scheme
Question 15
Expand `(2-x)(1+2x)^(-3/2)` in ascending powers of `x`, up to and including the term in `x^2`, simplifying the coefficients.
Medium
Mark as Complete
Mark Scheme
Question 16
Expand `frac{1+3x}{sqrt(1+2x) }`in ascending powers of `x` up to and including the term in `x^2`, simplifying the coefficients.
Medium
Mark as Complete
Mark Scheme
Question 17
Express `frac{7x^2-3x+2}{x(x^2+1)}` in partial fractions.
Medium
Mark as Complete
Mark Scheme
Question 18
Show that for small values of `x^2`, `(1-2x^2)^-2-(1+6x^2)^(2/3)≈kx^4`, where the value of the constant `k` is to be determined.
Medium
Mark as Complete
Mark Scheme
Question 19
Let `f(x)=frac{2x^2-7x-1}{(x-2)(x^2+3)}`.
(a) Express `f(x)` in partial fractions.
(b) Hence obtain the expansion of `f(x)` in ascending powers of `x`, up to and including the term in `x^2`.
Hard
Mark as Complete
Mark Scheme
Question 20
Let `f(x)=frac{3x}{(1+x)(1+2x^2)}`.
(a) Express `f(x)` in partial fractions.
(b) Hence obtain the expansion of `f(x)` in ascending powers of `x`, up to and including the term in `x^2`.
Hard
Mark as Complete
Mark Scheme
Question 1
Let `f(x)=frac{24x+13}{(1-2x)(2+x)^2}`
(a) Express `f(x)` in partial fractions.
(b) Hence obtain the expansion of `f(x)` in ascending powers of `x`, up to and including the term in `x^2`.
(a)
`A/(1-2x)+B/(2+x)+C/((2+x)^2)`
`A(2+x)^2+B(1-2x)(2+x)+C(1-2x)=24x+13`
Obtain: `A = 4`, `B = 2` and `C = -7`
Obtain the values, mark the form `A/(1-2x)+(Dx+E)/((2+x)^2)` where `A=4, D=2, E=-3`
(b)
Use a correct method to find the first two terms of the expansion of `(1-2x)^-1, (2+x)^-1, (2+x)^-2, (1+x/2)^-1 or (1+x/2)^-2`
Obtain correct un-simplified expansions up to the term in `x^2`of each partial fraction
`A(1+(-1)(-2x)+frac{(-1)(-2)}{2}(-2x)^2+… A)=4`
`B/2(1+(-1)(x/2)+frac{(-1)(-2)}{2}(x/2)^2+… B)=2`
`C/4(1+(-2)(x/2)+frac{(-2)(-3)}{2}(x/2)^2+… C)=-7`
`=4(1+2x+4x^2)+2/2(1-x/2+(x/4)^2-7/4(1-x+3/4x^2))`
`13/4+37/4x+239/16x^2`
Question 2
Let`f(x)=frac{17x^2-7x+16}{(2+3x^2)(2-x)}`
(a) Express `f(x)` in partial fractions
(b) Hence obtain the expansion of `f(x)`in ascending powers of `x`, up to and including the term in `x^3`
(c) State the set of values of `x` for which the expansion in (b) is valid. Give your answer in an exact form.
(a)
State or imply the form `frac{Ax+B}{2+3x^2}+C/(2-x)`
Use a correct method for finding a coefficient: `(Ax + B)(2 – x) + C(2 + 3x^2) = (3C −A)x^2 + (2A −B)x + (2B + 2C) = 17x^2 – 7x + 16`.
Obtain `A = -2`, `B = 3` and `C = 5`: `frac{-2x+3}{2+3x^2}+5/(2-x)`
(b)
Use a correct method to find the first two terms of the expansion: `(-2x+3)/(2+3x^2)+5/(2-x)=(-2x+3)/(x)(1+(3x^2)/2)^-1+5(2-x)^-1`
`(2-x)^-1= 2^-1+(-1)2^-2(-x)+(-1)(-2)2^-3((-x)^2)/(2!)`
`(1+(3x^2)/2)^-1=1-(3x^2)/2`
`=frac{-2x+3}{x}(1+(3x^2)/2)^-1+5(2-x)^-1`
`= frac{-2x+3}{2}(1-(3x^2)/2)+5(2^-1+(-1)2^-2(-x)+(-1)(-2)2^-3((-x^2))/(2!))`
`= 3/2+5/2+(-1+5/4)x+(-9/4+5/8)x^2+(3/2+5/16)x^3`
Obtain final answer: `4+1/4x-13/8x^2+29/6x^3`
(c)
Final answer:`|x| or `-sqrt(2/3) < x < sqrt(2/3)`
Question 3
Given that `frac{x^3+x^2-7}{x-3}=Ax^2+Bx+C+D/(x-3)`, find the values of A, B, C and D.
`(x^3+x^2-7)/(x-3)=x^2+4x+12+29/(x-3)`
`A=1`, `B=4`, `C=12` and `D=29`.
Note: full process
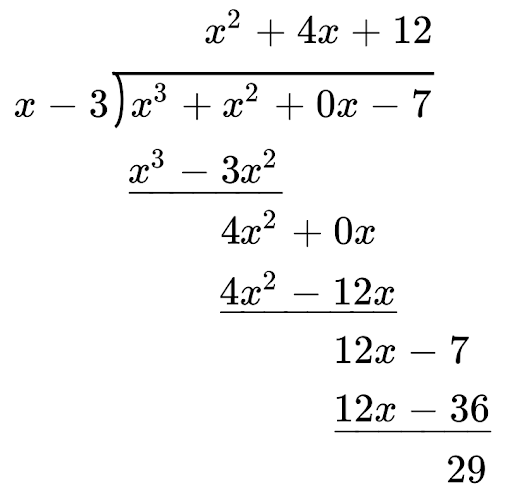
Question 4
Given that `(2x^4+3x^3+4x^2+5x+6)/(x^3+2x)=Ax+B+(Cx+D)/(x^3+2x)`, find the values of A, B, C and D.
`(2x^4+3x^3+4x^2+5x+6)/(x^3+2x)=2x+3+(-x+6)/(x^3+2x)`
`A=2, B=3, C=-1` and `D=6`.
Note: full process
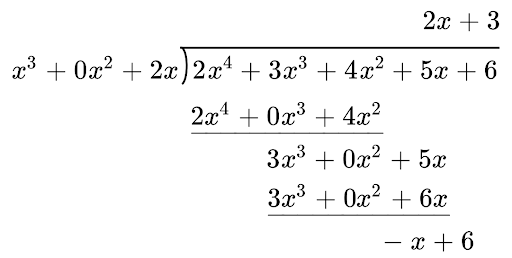
Question 5
(a) Express `2/(x(x+2)` in partial fraction.
(b) Find an expression for the sum of the first `n` terms of the series.
`2/((1)xx(3))+2/((2)xx(4))+2/((3)xx(5))+2/((4)xx(6))+2/((5)xx(7))+…`
(c) Find the sum to infinity of this series.
(a)
`2/(x(x+2))=A/x+B/(x+2)`
`A(x+2)+Bx=2`
Letting`x=0` and `x=2`
Getting `A=1` and `B=-1`
`2/(x(x+2))=1/x-1/(x+2)`
(b)
Using the result from part a:
`2/((1)xx(3))+2/((2)xx(4))+2/((3)xx(5))+2/((4)xx(6))+2/((5)xx(7))+…`
`=(1/1-1/3)+(1/2-1/4)+(1/3-1/5)+(1/4-1/6)+…+(1/(n-2)-1/n)+(1/(n-1)-1/(n+1)`
`=1+1/2+1/3-1/3+1/4-1/4+1/5-1/5+…+1/n-1/n-1/(n+1)-1/(n+2)`
`=1+1/2-1/(n+1)-1/(n+2)`
`=3/2-1/(n+1)-1/(n+2)`
(c)
Sum to infinity
`3/2-1/(n+1)-1/(n+2) -> 3/2-0-0=3/2` as `n→∞`
Question 6
Given that `(1-3x)^-4-(1+2x)^(3/2)≈9x+kx^2` for small values of `x`, find the value of the constant.
`(1-3x)^-4`
`=1+(-4)(-3x)+frac{(-4)(-5)}(2!)(-3x)^2+…`
`=1+12x+90x^2+…`
`(1+2x)^(3/2)`
`=1+(3/2)(2x)+frac{(3/2)(1/2)}{2!}(2x)^2+…`
`=1+3x+frac{(3)(4)}{(4)(2)}x^2+…`
`=1+3x+3/2x^2+…`
So
`(1-3x)^-4-(1+2x)^(3/2)`
`=1+12x+90x^2+…-(1+3x+3/2x^2+… )`
`=1-1+12x-3x+(30-3/2)x^2+…`
`=9x+177/2x^2+…`
So `k=177/2`
Question 7
Given that `a/(1-x)+b/(1+2x)≈-3+12x` for small values of `x`, find the value of `a` and the value of `b`.
`1/(1-x)=(1-x)^-1=1+(-1)(-x)+frac{(-1)(-2)}{2!}x^2+…=1+x+x^2+…`
`1/(1+2x)=(1+2x)^-1=1+(-1)(2x)+frac{(-1)(-2)}{2!}(2x)^2+…=1-2x+4x^2+…`
So `a/(1-x)+b/(1+2x)=a(1+x+x^2+…)+b(1-2x+4x^2+…)`
`=-3+12x`
Equating constants: `-3=a+b` [1]
Equating coefficient of x: `12=a-2b` [2]
`[1]-[2]`:
`3b=15→b=5→a=2`
Question 8
When `(1+ax)^-3`, where a is a positive constant, is expanded the coefficients of x and `x^2` are equal.
(a) Find the value of `a`.
(b) When `a` has this value, obtain the first `5` terms in the expansion.
(a)
`(1+ax)^-3=1+(-3)(ax)+frac{(-3)(-4)}{2!}(ax)^2+…`
`=1-3ax+6a^2x^2+…`
Using the fact that the coefficient of `x^2` and x are equal:
`6a^2=-3a→a=0 or a=-1/2`
But `a<0` so `a=-1/2`
(b)
`(1+ax)^-3=1+(-3)(ax)+frac{(-3)(-4)}{2!}(ax)^2+frac{(-3)(-4)(-5)}{3!}(ax)^3+frac{(-3)(-4)(-5)(-6)}{4!}(ax)^4+…`
`=1-3ax+6a^2x^2-10a^3x^3+15a^4x^4+…`
`=1+3/2x+3/2x^2+5/4x^3+15/16x^4+…`
Question 9
When `(3-2x)(1+ax)^(2/3)` is expanded the coefficient of `x^2` is `-15`. Find the two possible values of `a`.
`(1+ax)^(2/3)=1+(2/3)(ax)+frac{(2/3)(1/3)}{2!}(ax)^2+…`
`=1+2/3ax-1/9a^2x^2+…`
So`(3-2x)(1+ax)^(2/3)`
`=(3-2x)(1+2/3ax-1/9a^2x^2+…)`
Using the fact that the coefficient of `x^2` is `-15`:
`3(-1/9a^2)-2(2/3a)=-1/3a^2-4/3a=-15`
`a^2+4a-45=0→a=-9 or a=5`
Question 10
The first `3` terms in the expansion of
`(1+ax)^n`are `1-24x+384x^2`.
(a) Find the value of `a` and the value of `n`.
(b) Hence find the term in `x^3`.
(a)
`(1+ax)^n=1+n(ax)+frac{n(n-1)}{2!}(ax)^2+…`
`=1+anx+1/2n(n-1)a^2x^2+…`
`=1-24x+384x^2+…`
Equating coefficients of`x`: `an=-24`
Equating coefficients of `x^2`: `1/2n (n-1)a^2=384→n (n-1)a^2=768`
Solve 2 equations [1] and [2] by substituting:`a=8` and `n=-3`
(b)
Term in `x^3`:
`frac{n(n-1)(n-2)}{3!}(ax)^3=frac{(-3)(-4)(-5)}{6}(8x)^3=-5120x^3`
Question 11
In the expansion of `sqrt(3+ax )` where `a≠0`, the coefficient of the term in `x^2` is `3` times the coefficient of the term in `x^3`. Find the value of `a`.
`(3+ax)^(1/2)=3^(1/2)(1+a/3x)^(1/2)`
`=sqrt3{1+(1/2)(a/3x)+frac{(1/2)(-1/2)}{2!}(a/3x)^2+frac{(1/2)(-1/2)(-3/2)}{3!}(a/3x)^3+…}`
Using the fact that the coefficient of `x^2` is three times the coefficient of `x^3`:
`-frac{aroot(2)3}{72}=(3)frac{sqrt3}{(16)(27)}a^3→a=-2`
Question 12
(a) Find the first `4` terms in the expansion of `(1+2/x)^-1`, where `|2/x|<1`.
(b) Show that`(1+2/x)^-1=x/(x+2)=x/2(1+x/2)^-1`.
(a)
`(1+2/x)^-1=1+(-1)(2/x)+frac{(-1)(-2)}{2!}(2/x)^2+frac{(-1)(-2)(-3)}{3!}(2/x)^3+…`
`=1-2/x+4/(x^2)-8/(x^3)+…`
(b)
`(1+2/x)^-1=((x+2)/x)^-1=x/(x+2)`
and
`(1+2/x)^-1=[2/x(x/2+1)]^-1=(2/x)^-1(x/2+1)^-1=x/2(1+x/2)^-1`
Question 13
(a) Find the first `4` terms in the expansion of `x/2(1+x/2)^-1`, where `|x/2|<1`.
(b) Explain why your expansion are diffferent from the above question: `(1+2/x)^-1=x/(x+2)=x/2(1+x/2)^-1`.
(a)
`x/2(1+x/2)^-1=x/2{1+(-1)(x/2)+frac{(-1)(-2)}{2!}(x/2)^2+frac{(-1)(-2)(-3)}{3!}(x/2)^3+…}`
`=x/2-x^2/4+x^3/8-x^4/16+…`
(b)
They are valid for different ranges of `x`, so the expansion is different.
Question 14
Expand `root(3)(1-6x)` in ascending powers of `x` up to and including the term in `x^3`, simplifying the coefficients.
`(1-6x)^(1/3)=1+(1/3)(-6x)+frac{(1/3)(-2/3)}{2!}(-6x)^2+frac{(1/3)(-2/3)(-5/3)}{3!}(-6x)^3+…`
`=1-2x-4x^2-40/3x^3+…`
Question 15
Expand `(2-x)(1+2x)^(-3/2)` in ascending powers of `x`, up to and including the term in `x^2`, simplifying the coefficients.
`(1+2x)^(-3/2)=1+(-3/2)(2x)+frac{(-3/2)(-5/2)}{2!}(2x)^2+…`
`=1-3x+15/2x^2+…`
`(2-x)(1+2x)^(-3/2)=(2-x)(1-3x+15/2x^2+… )`
`=2-7x+18x^2+…`
Question 16
Expand `frac{1+3x}{sqrt(1+2x) }`in ascending powers of `x` up to and including the term in `x^2`, simplifying the coefficients.
`(1+2x)^(-1/2)=1+(-1/2)(2x)+frac{(-1/2)(-3/2)}{2!}(2x)^2+…`
`=1-x+3/2x^2-…`
`=(1+3x)(1+2x)^(-1/2)=(1+3x)(1-x+3/2x^2-…)`
`=1+2x-3/2x^2+…`
Question 17
Express `frac{7x^2-3x+2}{x(x^2+1)}` in partial fractions.
`frac{7x^2-3x+2}{x(x^2+1)}=A/x+frac{Bx+C}{x^2-1 }`
`7x^2-3x+2=A(x^2+1)+(Bx+C)x`
Letting `x=0`:
`A=2`
Equating coefficients of `x^2`:
`7=A+B`
`B=5`
Equating coefficients of `x`:
`C=-3`
`frac{7x^2-3x+2}{x(x^2+1)}=2/x+frac{5x-3}{x^2-1}`
Question 18
Show that for small values of `x^2`, `(1-2x^2)^-2-(1+6x^2)^(2/3)≈kx^4`, where the value of the constant `k` is to be determined.
`(1-2x^2)^-2`
`=1+(-2)(-2x^2)+frac{(-2)(-3)}{2!}(-2x^2)^2+…`
`=1+4x^2+12x^4+…`
`(1+6x^2)^(2/3)`
`=1+(2/3)(6x^2)+frac{(2/3)(-1/3)}{2!}(6x^2)^2+…`
`=1+4x^2-8x^4+…`
`(1-2x^2)^-2-(1+6x^2)^(2/3)=(1+4x^2+12x^4+…)+(1+(2/3)(6x^2)+frac{(2/3)(-1/3)}{2!}(6x^2)^2+…=16x^4+…)`
So `k=6`
Question 19
Let `f(x)=frac{2x^2-7x-1}{(x-2)(x^2+3)}`.
(a) Express `f(x)` in partial fractions.
(b) Hence obtain the expansion of `f(x)` in ascending powers of `x`, up to and including the term in `x^2`.
(a)
`frac{2x^2-7x-1}{(x-2)(x^2+3)}=frac{A}{x-2}+frac{Bx+C}{x^2+3}`
`2x^2-7x-1=A(x^3+3)+(Bx+C)(x-2)`
Letting`x=2, x=0` to find `A=-1, C=-1`
`A+B=-2→B=3`
`frac{2x^2-7x-1}{(x-2)(x^2+3)}=-frac{1}{x-2}+frac{3x-1}{x^2+3}`
(b)
`-frac{1}{x-2}+frac{3x-1}{x^2+3}`
`(x-2)^-1=(-2)^-1 (1-x/2)^-1=-1/2 {1+(-1)(-x/2)+frac{(-1)(-2)}{2!}(-x/2)^2+… }`
`=-1/2-x/4+x^2/8+…`
`(x^2+3)^-1=3^-1(1+x^2/3)^-1=1/3 {1+(-1)(x^2/3)+frac{(-1)(-2)}{2!}(x^2/3)^2+… }`
`=1/3-x^2/9+x^4/27+…`
`(3x-1)(x^2+3)^-1=(3x-1)(1/3-x^2/9+x^4/27+…)`
`=-1/3+x+x^2/9-…`
So`f(x)=-1/(x-2)+(3x-1)/(x^2+3)=-(-1/2-x/4+x^2/8+…)+(-1/3+x+x^2/9-…)=1/6+5/4x+17/72x^2+…`
Question 20
Let `f(x)=frac{3x}{(1+x)(1+2x^2)}`.
(a) Express `f(x)` in partial fractions.
(b) Hence obtain the expansion of `f(x)` in ascending powers of `x`, up to and including the term in `x^2`.
(a)
`frac{3x}{(1+x)(1+2x^2)}=A/(1+x)+(Bx+C)/(1+2x^2)`
`3x=A(1+2x)^2+(Bx+C)(1+x)`[1]
Letting `x=-1, x=0` to find `A=-1, C=1, B=2`
`frac{3x}{(1+x)(1+2x^2)}=-1/(1+x)+(2x+1)/(1+2x^2)`
(b)
`(x+1)^-1=1-x+x^2-x^3+…`
`(1+2x^2)^-1=1-2x^2+4x^4+…`
`(2x+1)(1+2x^2)^-1=1+2x-2x^2-4x^3+…`
So `f(x)=-1/(1+x)+(2x+1)/(1+2x)^2=3x-3x^2-3x^3+…`
Question 1
Let `f(x)=frac{24x+13}{(1-2x)(2+x)^2}`
(a) Express `f(x)` in partial fractions.
(b) Hence obtain the expansion of `f(x)` in ascending powers of `x`, up to and including the term in `x^2`.
Question 2
Let`f(x)=frac{17x^2-7x+16}{(2+3x^2)(2-x)}`
(a) Express `f(x)` in partial fractions
(b) Hence obtain the expansion of `f(x)`in ascending powers of `x`, up to and including the term in `x^3`
(c) State the set of values of `x` for which the expansion in (b) is valid. Give your answer in an exact form.
Question 3
Given that `frac{x^3+x^2-7}{x-3}=Ax^2+Bx+C+D/(x-3)`, find the values of A, B, C and D.
Question 4
Given that `(2x^4+3x^3+4x^2+5x+6)/(x^3+2x)=Ax+B+(Cx+D)/(x^3+2x)`, find the values of A, B, C and D.
Question 5
(a) Express `2/(x(x+2)` in partial fraction.
(b) Find an expression for the sum of the first `n` terms of the series.
`2/((1)xx(3))+2/((2)xx(4))+2/((3)xx(5))+2/((4)xx(6))+2/((5)xx(7))+…`
(c) Find the sum to infinity of this series.
Question 6
Given that `(1-3x)^-4-(1+2x)^(3/2)≈9x+kx^2` for small values of `x`, find the value of the constant.
Question 7
Given that `a/(1-x)+b/(1+2x)≈-3+12x` for small values of `x`, find the value of `a` and the value of `b`.
Question 8
When `(1+ax)^-3`, where a is a positive constant, is expanded the coefficients of x and `x^2` are equal.
(a) Find the value of `a`.
(b) When `a` has this value, obtain the first `5` terms in the expansion.
Question 9
When `(3-2x)(1+ax)^(2/3)` is expanded the coefficient of `x^2` is `-15`. Find the two possible values of `a`.
Question 10
The first `3` terms in the expansion of
`(1+ax)^n`are `1-24x+384x^2`.
(a) Find the value of `a` and the value of `n`.
(b) Hence find the term in `x^3`.
Question 11
In the expansion of `sqrt(3+ax )` where `a≠0`, the coefficient of the term in `x^2` is `3` times the coefficient of the term in `x^3`. Find the value of `a`.
Question 12
(a) Find the first `4` terms in the expansion of `(1+2/x)^-1`, where `|2/x|<1`.
(b) Show that`(1+2/x)^-1=x/(x+2)=x/2(1+x/2)^-1`.
Question 13
(a) Find the first `4` terms in the expansion of `x/2(1+x/2)^-1`, where `|x/2|<1`.
(b) Explain why your expansion are diffferent from the above question: `(1+2/x)^-1=x/(x+2)=x/2(1+x/2)^-1`.
Question 14
Expand `root(3)(1-6x)` in ascending powers of `x` up to and including the term in `x^3`, simplifying the coefficients.
Question 15
Expand `(2-x)(1+2x)^(-3/2)` in ascending powers of `x`, up to and including the term in `x^2`, simplifying the coefficients.
Question 16
Expand `frac{1+3x}{sqrt(1+2x) }`in ascending powers of `x` up to and including the term in `x^2`, simplifying the coefficients.
Question 17
Express `frac{7x^2-3x+2}{x(x^2+1)}` in partial fractions.
Question 18
Show that for small values of `x^2`, `(1-2x^2)^-2-(1+6x^2)^(2/3)≈kx^4`, where the value of the constant `k` is to be determined.
Question 19
Let `f(x)=frac{2x^2-7x-1}{(x-2)(x^2+3)}`.
(a) Express `f(x)` in partial fractions.
(b) Hence obtain the expansion of `f(x)` in ascending powers of `x`, up to and including the term in `x^2`.
Question 20
Let `f(x)=frac{3x}{(1+x)(1+2x^2)}`.
(a) Express `f(x)` in partial fractions.
(b) Hence obtain the expansion of `f(x)` in ascending powers of `x`, up to and including the term in `x^2`.