Question 1
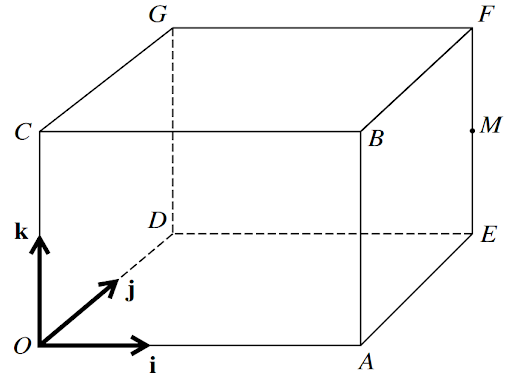
In the diagram, OABCDEFG is a cuboid in which `OA = 3` units, `OC = 2` units and `OD = 2` units. Unit vectors i, j and k are parallel to OA, OD and OC respectively. M is the midpoint of EF.
a. Find the position vector of M.
The position vector of P is `i + j + 2k`.
b. Calculate angle `PAM`.
c. Find the exact length of the perpendicular from P to the line passing through O and M.
Medium
Mark as Complete
Mark Scheme
Question 2
The line l has equation`r=i-2j-3k+λ(-i+j+2k)`. The point A and B have position vectors `-2i+2j-k` and `3i-j+k` respectively.
a. Find a unit vector in the direction of `l`.
The line m passes through the points A and B.
b. Find a vector equation for `m`.
c. Determine whether lines `l` and `m` are parallel, intersect or are skew.
Hard
Mark as Complete
Mark Scheme
Question 3
Relative to the origin`O`, the position vectors of point A, B and C are given by `vec(OA)=(2 3 7)`, `vec(OB)=(3m 1 1)` and `vec(OC)=(4 -m -m(m+1))`
a. It is given that `vec(OA)=vec(OB)`. Find the angle `OAB`.
b. Find the vector equation of the line `AC`.
Medium
Mark as Complete
Mark Scheme
Question 4
With respect to the origin `O`, the position vectors of the points A and B are given by `vec(OA)=(-2 0 6)` , `vec(OB)=(1 -1 4)`.
a. Find whether or not the vectors `vec(OA)` and `vec(OB)` are perpendicular.
b. Write down the vector `vec(AB)`.
c. Find a vector equation of the line `AB`.
d. The vector equation of the line `L` is given by `r=7i-12j+7k+μ(-3i+10j-5k)`. Show that the lines `AB` and `L` intersect and find the position vector of the point of intersection.
Hard
Mark as Complete
Mark Scheme
Question 5
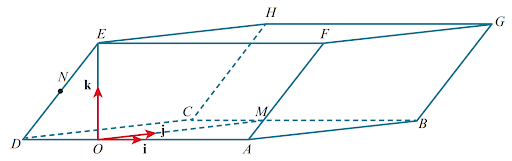
The diagram shows a prism, `ABCDEFGH`, with a parallelogram-shaped uniform cross-section.
The point `E` is such that `OE`is the height of the parallelogram. The point `M` is such that `vec(OM)` is parallel to `vec(DC)` and `N` is the midpoint of `DE`. The side `OD` has a length of `5` units. The unit vectors, i j and k are parallel to`vec(OA), vec(OM)` and `vec(OE)`, respectively.
The position vectors of the points `A`, `E`, `C` and `M` are given by `vec(OA)=9i`, `vec(OM)=15j` and `vec(OE)=12k`.
a. Express the vectors `vec(AH)` and `vec(NH)` in term of i, j and k.
b. Use a vector method to find angle `AHN`.
c. Write down a vector equation of the line `AH`.
Hard
Mark as Complete
Mark Scheme
Question 6
The position vectors of A, B and C relative to an origin O are given by `vec(OA)=(6 3 2)`, `vec(OB)=(2 n -1)` and `vec(OC)=(8 9 0)` , where `n` is constant.
a. Find the value of `n` for which `|vec(AB)|=|vec(CB)|`.
b. In this case, use a scalar product to find angle ABC.
Medium
Mark as Complete
Mark Scheme
Question 7
a. Given the vector `8i-2j+5k`and `i+2j+pk`are perpendicular, find the value of the constant `p`.
The line `L_1` passes through the point `(-3, 1, 5)` and is parallel to the vector `7i-j+k`.
b. Write down a vector equation of the line `L_1`.
c. The line `L_2` has vector equation `r=i-2j+2k+μ(i+8j-3k)`. Show that `L_1` and `L_2` do not intersect.
Medium
Mark as Complete
Mark Scheme
Question 8
The origin `O` and the points`A, B` and `C`are such that `OABC` is a rectangle. With respect to `O`, the position vectors of the points `A` and `B` are `-4i+pj-6k` and `-10i-2j-10k`.
a. Find the value of the positive constant `p`.
b. Find a vector equation of the line `AC`.
c. Show that the line `AC` and the line, `L`, with vector equation `r=3i+7j+k+μ(-4i-4j-3k)` intersect and find the position vector of the point of intersection.
d. Find the acute angle between the lines `AC` and `L`.
Medium
Mark as Complete
Mark Scheme
Question 9
Relative to the origin `O`, the points `A`, `B`, `C` and `D` have position vectors `vec(OA)=4i+2j-k`, `vec (OB)=2i-2j+5k`, `vec(OC)=2j+7k`, `vec(OD)=-6i+22j+9k`
a. Use a scalar product to show that angle `ABC` is a right angle.
b. Show that `vec(AD)=kvec(BC)` where `k` is a constant, and explain what this means.
c. The point `E` is the midpoint of the line `AD`. Find a vector equation of the line `EC`.
Medium
Mark as Complete
Mark Scheme
Question 10
With respect to the origin `O`, the points `A`, `B`, `C` and `D` have position vectors given by `vec(OA)=-3i+j+8k`, `vec(OB)=-10i+2j+15k`, `vec(OC)=5i-2j-2k`, `vec(OD)=i+6j+10k`
a. Calculate the acute angle between the lines `AB` and `CD`.
b. Prove that the lines `AB` and `CD` intersect.
c. The point `E` has position vector `5i+3j+4k`. Show that the perpendicular distance from `E` to the line `CD` is equal to`sqrt5`.
Hard
Mark as Complete
Mark Scheme
Question 11
`PQRS` is a rhombus. The coordinates of the vertices `P`, `Q` and `S` are `(9, 2, 4)`, `(-0.5, 6, 6.5)` and `(4.5, -4, -3.5)`, respectively.
a. Find the vector`vec(PQ)` and `vec(PS)`.
b. Find the coordinate of `R`.
c. Show that `PQRS` is in fact a square and find the length of the side of the square.
d. The point `T` is the centre of the square. Find the coordinates of `T`.
The point `V`has coordinates `(5, 17.5, -13.5)`.
e. Find a vector equation of the line `VT`.
f. Verify that `T` is the foot of the perpendicular from `V` to `PR`.
g. Describe the solid `VPQRS`.
Hard
Mark as Complete
Mark Scheme
Question 12
The point `P` and `Q` have coordinates `(0, 19, -1)` and `(-6, 26, -11)`, respectively.
The line `L` has vector equation
`r=3i+9j+2k+λ(3i-10j+3k)`
a. Show that the point `P` lies on the line `L`.
b. Find the magnitude of `|vec(PQ)|`.
c. Find the obtuse angle between `PQ` and `L`.
d. Calculate the perpendicular distance from `Q` to the line `L`.
Medium
Mark as Complete
Mark Scheme
Question 13
The point A and B have coordinates `(7, 1, 6)` and `(10, 5, 1)`, respectively.
a. Write down a vector equation of the line `AB.`
b. The point `P` lies on the line`AB`. The point `Q` has coordinate `(0, -5, 7)`. Given that `PQ` is perpendicular to `AB`, find a vector equation of the line `PQ`.
c. Find the shortest distance from `Q` to `AB`.
Medium
Mark as Complete
Mark Scheme
Question 14
The line `L_1` has vector equation`r=3i+2j+5k+λ(4i+2j+3k)`.
The point `A(3, p, 5)` and `B(q, 0, 2)`, where `p` and `q` are constant, lie on the line `L_1`.
a. Find the value of `p` and the value of `q`.
The line `L_2` has vector equation `r=3j+k+μ(7i+j+7k)`.
b. Show that `L_2` and `L_1` intersect and find the position vector of the point of intersection.
c. Find the acute angle between `L_2` and `L_1`.
Hard
Mark as Complete
Mark Scheme
Question 15
Given that the lines with vector equations
`r=2i+9j+k+λ(i-4j+5k)`
And `r=11i+9j+pk+μ(-i-2j+16k)` intersect at the point `P`, find the value of `p` and the position vector of the point `P`.
Medium
Mark as Complete
Mark Scheme
Question 16
Three lines,`L_1, L_2` and`L_3`, have vector equations
`r=16i-4j-6k+λ(-12i+4j+3k)`
`r=16i+28j+15k+μ(8i+8j+5k)`
`r=i+9j+3k+v(4i-12j-8k)`
The 3 points of intersection of these lines form an acute-angled triangle.
For this triangle, find:
a. The position vector of each of the three vertices.
b. The size of each of the interior angles.
c. the length of each side.
Hard
Mark as Complete
Mark Scheme
Question 17
The line `L_1` passes through the points `(3, 7, 9)` and `(-1, 3, 4)`.
a. Find a vector equation of the line `L_1`.
b. The line `L_2` has vector equation `r=i+2j+k+μ(3j+2k)`
Show that `L_1` and `L_2` do not intersect.
Medium
Mark as Complete
Mark Scheme
Question 18
The point `A` has coordinates `(1, 0, 5)` and the point `B` has coordinates `(-1, 2, 9)`.
a. Find the vector `vec(AB)`.
b. Write down a vector equation of the line `AB`.
c. Find the acute angle between the line `AB` and the line `L` with vector equation`r=i+3j+4k+μ(-i-2j+3k)`.
d. Find the point of intersection of the line `AB` and the line `L`.
Medium
Mark as Complete
Mark Scheme
Question 19
The vector equation of the line `L_1` is given by
`(x y z) =(-3 0 8) +t(4 -1 -3)`.
a. Find the vector equation of the line `L_2` that is parallel to `L_1` and which passes through the point `A(5, -3, 2)`.
b. Show that `A(5, -3, 2)` is the foot of the perpendicular from the point `B(4, -7, 2)` to the line `L_2`.
Medium
Mark as Complete
Mark Scheme
Question 20
The point `A`, `B` and `C` are position vectors relative to the origin `O`, given by `vec(OA)=(3 1 5)`, `vec(OB)=(0 -1 2)` and `vec(OC)=(1 2 3)`
a. Find a vector equation for the line `L` passing through `A` and `B`.
b. The line through `C`, perpendicular to`L`, meets `L` at the point `N`. Find the exact coordinates of `N`.
Medium
Mark as Complete
Mark Scheme
Question 1

In the diagram, OABCDEFG is a cuboid in which `OA = 3` units, `OC = 2` units and `OD = 2` units. Unit vectors i, j and k are parallel to OA, OD and OC respectively. M is the midpoint of EF.
a. Find the position vector of M.
The position vector of P is `i + j + 2k`.
b. Calculate angle `PAM`.
c. Find the exact length of the perpendicular from P to the line passing through O and M.
a. Obtain `3i + 2j + k = (3, 2, 1)`
b.
`vec(AM)` or `vec(AP)` correct, `vec(AM)= 2j + k` , or `vec(AP) = –2i + j + 2k`
Carry out correct process for evaluating the scalar product of `vec(AM)` or `vec(AP)`
Using the correct process for the moduli, divide the scalar product by the product of the moduli and obtain the inverse cosine of the result: angle `PAM = cos^-1 frac{4}{3sqrt5}`
Obtain answer `53.4°`
c.
Find `vec(PQ)` (or `vec(QP)` ) for a general point Q on the line passing through O and M. `PQ = - (i + j + 2k) + μ(3i + 2j + k)`
Calculate the scalar product of `vec(PQ)` and a direction vector for the line passing through O and M and equate to zero
Solve and obtain correct solution `μ= -1/2`
Carry out method to calculate `PQ =sqrt( 5^2+0+1.5^2)`
Obtain answer`sqrt10/2`
Question 2
The line l has equation`r=i-2j-3k+λ(-i+j+2k)`. The point A and B have position vectors `-2i+2j-k` and `3i-j+k` respectively.
a. Find a unit vector in the direction of `l`.
The line m passes through the points A and B.
b. Find a vector equation for `m`.
c. Determine whether lines `l` and `m` are parallel, intersect or are skew.
a.
Use correct process for modulus on direction vector of `l`: `sqrt((-1)^2+1^2+2^2)` or `sqrt((-λ)^2+lambda^2+lambda^2)`
Unit vector: `(+)/(-) (1/sqrt6)(-i+j+2k)`
b.
Use a correct method to form an equation for line `m`
Obtain `r=-2i+2j-k+mu_1(-5i+3j-2k)`
c.
`( −5, 3, −2) ≠ d (− 1, 1, 2)` or `( −5, 3, −2).(− 1, 1, 2) ≠ 0`: lines are not parallel
Express `l` or `m` in component form`(–2 – 5mu_1, 2 + 3mu_1, –1 – 2mu_1)`or`(3 – 5mu_2, − 1 + 3mu_2, 1 – 2mu_2)` or `(1 – λ, –2 + λ, –3 + 2λ)`
Equate two pairs of components of general points on `l` and their `m` and solve simultaneously for `lambda` or for `mu`
Obtain correct answer for `lambda` or `mu` : `lambda =112`, `mu_1=1/2`
Determine that all three equations are not satisfied and the lines fail to intersect and conclude the lines are skew.
Dependent on `4` previous marks gained
Question 3
Relative to the origin`O`, the position vectors of point A, B and C are given by `vec(OA)=(2 3 7)`, `vec(OB)=(3m 1 1)` and `vec(OC)=(4 -m -m(m+1))`
a. It is given that `vec(OA)=vec(OB)`. Find the angle `OAB`.
b. Find the vector equation of the line `AC`.
a.
`vec(AB)=(3m 1 1) -(2 3 7) =(3m-2 -2 -6)`
`vec(AB)=vec(OC )`
`(3m-2 -2 -6 )=(4 -m -m(m+1))`
`m=2`
`vec(AB)=(4 -2 -6) vec(AO)=(-2 -3 -7)`
`(4 -2 -6) xx (-2 -3 -7) =sqrt(16+4+36) sqrt(4+9+49)cos OAB`
`-8+6+42=sqrt(56) sqrt(62)cos OAB`
`OAB=(frac{40}{sqrt(56)sqrt(62)}) =47.2^o` (to `1` decimal place)
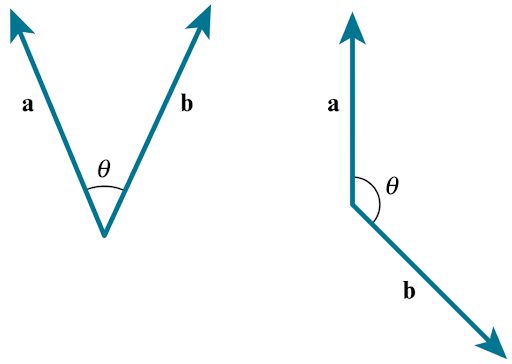
Note: Remember that, when you take the scalar product of two vectors, the angle used in the definition `a.b=|a||b|cos theta` is the angle produced when the two vectors are drawn tail to tail:
b.
`vec(AC)=c-a=(4 -2 -6) -(2 3 7) =(2 -5 -13)`
Equation of line:
`r=(2 3 7) +λ(2 -5 -13)`
Note: Remember that you can use any positive or negative multiple of the direction vector. It will still be an equation of the same line.
Question 4
With respect to the origin `O`, the position vectors of the points A and B are given by `vec(OA)=(-2 0 6)` , `vec(OB)=(1 -1 4)`.
a. Find whether or not the vectors `vec(OA)` and `vec(OB)` are perpendicular.
b. Write down the vector `vec(AB)`.
c. Find a vector equation of the line `AB`.
d. The vector equation of the line `L` is given by `r=7i-12j+7k+μ(-3i+10j-5k)`. Show that the lines `AB` and `L` intersect and find the position vector of the point of intersection.
a.
`vec(OA).vec(OB)=(-2)(1)+(0)(-1)+(6)(4)=22≠0`
Vector `vec(OA)` and`vec(OB)` are not perpendicular.
b.
`vec(AB)=b-a=3 -1 -2`
c.
`r=-2i+6k+λ(3i-j-2k)`
d.
Note: You can switch to column vectors if you find them easier to work with, as shown here.
`(-2 0 6) +s(3 -1 -2) =(7 -12 7) +t(-3 10 -5)`
`-2+3s=7-3t`
`3s+3t=9`
`s+t=3…………[1]→-s=-12+10t`
`s+10t=12…………[2]→6-2s=7-5t`
`2s-5t=-1…………[3]`
`[2]-[1]`
`9t=9`
`t=1`
Then from [1]:
`s=2`
Checking [3]:
`2s-5t=4-5=-1` [1]
This is consistent, so the lines intersect.
Position vector of the point of intersection is:
`(-2 0 6) +s(3 -1 -2) =(-2 0 6) +2(3 -1 -2) =(4 -2 2)`
Question 5

The diagram shows a prism, `ABCDEFGH`, with a parallelogram-shaped uniform cross-section.
The point `E` is such that `OE`is the height of the parallelogram. The point `M` is such that `vec(OM)` is parallel to `vec(DC)` and `N` is the midpoint of `DE`. The side `OD` has a length of `5` units. The unit vectors, i j and k are parallel to`vec(OA), vec(OM)` and `vec(OE)`, respectively.
The position vectors of the points `A`, `E`, `C` and `M` are given by `vec(OA)=9i`, `vec(OM)=15j` and `vec(OE)=12k`.
a. Express the vectors `vec(AH)` and `vec(NH)` in term of i, j and k.
b. Use a vector method to find angle `AHN`.
c. Write down a vector equation of the line `AH`.
a.
`vec(AH)=vec(AO)+vec(OE)+vec(EH)`
`=-9i+12k+15j`
`vec(NH)=vec(NE)+vec(EH)`
`=1/2 vec(DE)+vec(EH)`
`=1/2(5i+12k)+15j`
`=2.5i+15j+6k`
b.
`(-9i+15j+12k)cdot( 2.5i+15j+6k)=sqrt(81+225+144) sqrt(6.25+225+26)cos AHN`
`cos AHN =frac{-22.5+225+72}{sqrt(81+225+144} sqrt(6.25+225+26)}`
`AHN=37.7^o` (to `1` decimal place)
c.
`r=vec(OA)+λvec(AH)`
`=9i+λ(-9i+15j+12k)`
You could also use `1/3`of this direction vector, to get:
`r=9i+λ(-3i+5j+4k)`
Question 6
The position vectors of A, B and C relative to an origin O are given by `vec(OA)=(6 3 2)`, `vec(OB)=(2 n -1)` and `vec(OC)=(8 9 0)` , where `n` is constant.
a. Find the value of `n` for which `|vec(AB)|=|vec(CB)|`.
b. In this case, use a scalar product to find angle ABC.
a.
`vec(AB)=b-a=(-4 n-3 -3)`
`vec(CB)=b-c=(-6 n-9 -1)`
`(-4)^2+(n-3)^2+(-3)^2=(-6)^2+(n-9)^2+(-1)^2`
`16+n^2-6n+9+9=36+n^2-18n+81+1`
`12n+34=118`
`n=7`
b.
`vec(AB)=(-4 4 -3)`
`vec(CB)=(-6 -2 -1)`
`vec(AB) cdot vec(CB)=24-8+3=sqrt(16+16+9)sqrt(36+4+1)cos ABC`
`ABC=frac{19}{sqrt(41)sqrt(41)} =62.4^o`(to `1` decimal place)
Question 7
a. Given the vector `8i-2j+5k`and `i+2j+pk`are perpendicular, find the value of the constant `p`.
The line `L_1` passes through the point `(-3, 1, 5)` and is parallel to the vector `7i-j+k`.
b. Write down a vector equation of the line `L_1`.
c. The line `L_2` has vector equation `r=i-2j+2k+μ(i+8j-3k)`. Show that `L_1` and `L_2` do not intersect.
a.
`(8i-2j+2k) cdot (i+2j+pk)=0`
`8-4+5p=0`
`5p=-4`
`p=-4/5`
b.
`r=-3i+j+5k+λ(7i-j-k)`
c.
Note: When trying to find the intersection of two lines, you will form three equations with just two parameters. The two values you determine must satisfy ALL three equations to indicate an intersection. If the values do not satisfy all three, then the lines do not intersect.
`-3i+j+5k+λ(7i-j-k)=i-2j+2k+μ(i+8j-3k)`
`-3+7λ=1+μ`
`7λ-μ=4……….`[1]
`1-λ=-2+8μ`
`λ+8μ=3`
`7λ+56μ=21………`[2]
`[2]-[1]`:
`57μ=17`
`mu=17/57`
`λ=3-8(17/57)=35/57`
`k-"component"`
`5-λ=2-3 mu`
Using the value obtained above
`5-35/57=250/57≠2-3(17/57)=3/19`
Inconsistent equations, so the lines do not intersect.
Question 8
The origin `O` and the points`A, B` and `C`are such that `OABC` is a rectangle. With respect to `O`, the position vectors of the points `A` and `B` are `-4i+pj-6k` and `-10i-2j-10k`.
a. Find the value of the positive constant `p`.
b. Find a vector equation of the line `AC`.
c. Show that the line `AC` and the line, `L`, with vector equation `r=3i+7j+k+μ(-4i-4j-3k)` intersect and find the position vector of the point of intersection.
d. Find the acute angle between the lines `AC` and `L`.
a.
Using the fact that `vec(OA)` is perpendicular to `vec(AB)`:
`(-4i+pj-6k) cdot (-10i-2j-10k+4k-pj+6k)=0`
`(-4i+pj-6k) cdot (-6i-2+pj-4k)=0`
`24-p(2+p)+24=0`
`p^2+2p-48=0`
`(p+8)(p-6)=0`
`p=6`or `p=-8`
`p>0`
`p=6`
b.
Rectangle, so
`vec(AC)=vec(AB)+vec(BC)=-6i-8j-4k+(4i-6j+6k)`
`=-2i-14j+2k`
`r=vec(OA)+λvec(BC)=-4i+6j-6k+λ(-2i-14j+2k)`
c.
`-4i+6j-6k+λ(-2i-14j+2k)=3i+7j+k+μ(-4i-4j-3k)`
`-4-2λ=3-4μ`
`2λ-4μ=-7………`[1]
`6-14λ=7-4μ`
`14λ-4μ=-1………`[2]
`-6+2λ=1-3μ`
`2λ+3μ=7………`[3]
Solve system equation [1] and [2]:
`λ=1/2` and `μ=2`
`2λ+3μ=1+6=7` which is consistent with equation [3].
The lines intersect at the point with position vector -`4i+6j-6k+1/2(-2i-14j+2k)=-5i-j-5k`
d.
`(-2i-14j+2k) cdot (-4i-4j-3k)=sqrt(4+196+4) sqrt(16+16+9)cos`
`cos theta =58/(sqrt(204) sqrt(41))`
`θ=50.6^o` (to `1` decimal place)
Question 9
Relative to the origin `O`, the points `A`, `B`, `C` and `D` have position vectors `vec(OA)=4i+2j-k`, `vec (OB)=2i-2j+5k`, `vec(OC)=2j+7k`, `vec(OD)=-6i+22j+9k`
a. Use a scalar product to show that angle `ABC` is a right angle.
b. Show that `vec(AD)=kvec(BC)` where `k` is a constant, and explain what this means.
c. The point `E` is the midpoint of the line `AD`. Find a vector equation of the line `EC`.
a.
`vec(AB).vec(CB)=(-2 -4 6) .(2 -4 -2) =(-2)(2)+(-4)(-4)+(6)(-2)=0`
b.
`vec(AD)=(-10 20 10)` and `vec(BC)=(-2 4 2)`
So `vec(AD)=5vec(BC)`
Lines `AD` and `BC` are parallel.
c.
Position vector of `E`
`vec(OE)=1/2(vec(OA)+vec(OD))`
`=1/2(4i+2j-k-6i+22j+9k)`
`=1/2(-2i+24j+8k)`
`=-i+12j+4k`
Direction
`vec(EC)=2j+7k-(-i+12j+4k)`
`=i-10j+3k`
`r=-i+12j+4k+λ(i-10j+3k)`
Question 10
With respect to the origin `O`, the points `A`, `B`, `C` and `D` have position vectors given by `vec(OA)=-3i+j+8k`, `vec(OB)=-10i+2j+15k`, `vec(OC)=5i-2j-2k`, `vec(OD)=i+6j+10k`
a. Calculate the acute angle between the lines `AB` and `CD`.
b. Prove that the lines `AB` and `CD` intersect.
c. The point `E` has position vector `5i+3j+4k`. Show that the perpendicular distance from `E` to the line `CD` is equal to`sqrt5`.
a.
`vec(AB)=-7i+j+7k`
`vec(CD)=-4i+8j+12k`
`(-7i+j+7k) cdot (-4i+8j+12k)=sqrt(49+1+49) sqrt(16+64+144) cos theta`
`cos theta =frac{28+8+84}{sqrt(99)sqrt(224)}`
`θ=36.3^o` (to `1` decimal place)
b.
`AB:r=vec(OA)+λvec(AB)=-3i+j+8k+λ(-7i+j+7k)`
`CD:r=vec(OC)+μvec(CD)=5i-2j-2k+μ(-4i+8j+12k)`
Intersect if :
`-3i+j+8k+λ(-7i+j+7k)=5i-2j-2k+μ(-4i+8j+12k)`
`7λ-4μ=-8` [1]
`λ-8μ=-3` [2]
`7λ-12μ=-10` [3]
Solve system equations [1] and [2]: `λ=-1` and `μ=1/4`
Give the answer obtained to [3]
`(7)(-1)-(12)(1/4)=-10` which is consistent to [3]
Intersect at the point with position vector:
`-3i+j+8k+λ(-7i+j+7k)`
`=-3i+j+8k-(-7i+j+7k)`
`=4i+k`
c.
Equation of `CD`:
`r=5i-2j-2k+μ(-4i+8j+12k)`
Any point on `CD` will have a position vector that can be written in this form. Let `N` be the foot of the perpendicular from `E` to `CD`. `N` lies on the line, so
`N=5i-2j-2k+μ(-4i+8j+12k)`
`vec(EN)=5i-2j-2k+μ(-4i+8j+12k)-(5i+3j+4k)`
`=-4μi+(8μ-5)i+(12μ-6)k`
For shortest distance, `vec(EN)` must be perpendicular to the line `CD`
`vec(EN).vec(CD)=0`
`(-4μi+(8μ-5)i+(12μ-6)k.(-4i+8j+12k)=0`
`16μ+8(8μ-5)+12(12μ-6)=0`
`224μ-40-72=0`
`μ=1/2`
`vec(EN)=-4(1/2)i+(8(1/2)-5j)+(12(1/2)-6)k`
`vec(EN)=-2i-j`
`|vec(EN)|=sqrt(4+1)=sqrtr5`
Question 11
`PQRS` is a rhombus. The coordinates of the vertices `P`, `Q` and `S` are `(9, 2, 4)`, `(-0.5, 6, 6.5)` and `(4.5, -4, -3.5)`, respectively.
a. Find the vector`vec(PQ)` and `vec(PS)`.
b. Find the coordinate of `R`.
c. Show that `PQRS` is in fact a square and find the length of the side of the square.
d. The point `T` is the centre of the square. Find the coordinates of `T`.
The point `V`has coordinates `(5, 17.5, -13.5)`.
e. Find a vector equation of the line `VT`.
f. Verify that `T` is the foot of the perpendicular from `V` to `PR`.
g. Describe the solid `VPQRS`.
a.
`vec(PQ)=(-0.5-9 6-2 6.5-4) =(-9.5 4 2.5)`
`vec(PQ)=(4.5-9 -4-2 -3.5-4) =(-4.5 -6 -7.5)` b.
`vec(OR)=vec(OQ)+vec(QR_`
Rhombus, so `vec(QR)=vec(PS)`
`vec(OR)=vec(OQ)+vec(PS)=(-0.5 6 6.5) +(-4.5 -6 -7.5) =(-5 0 -1)`
`R(-5, 0, -1)`
c.
`vec(PQ).vec(PS)=(-9.5)(-4.5)+(4)(-6)(+2.5)(-7.5)=0`
PQ is perpendicular to PS, so the shape is a rectangle.
`|vec(PQ)|=sqrt(9.5^2+4^2+2.5^2)=sqrt112.5`
`|vec(PS)|= sqrt(4.5^2+6^2+7.5^2)=sqrt112.5`
Perpendicular sides have the same length, so it is a square.
d.
Midpoint of QS has position vector
`1/2(vec(OQ)+vec(OS))=1/2(4 2 3)`
`T(2, 1, 1.5)`
e.
For example`r=v+λ(t-v)`
`r=(5 17.5 -13.5) +λ(-3 -16.5 15)`
(f)
`vec(VT).vec(PR)=(-3 -16.5 15) .(-14 -2 -5) =42+33-75=0`
`VT` is perpendicular to `PR` and `V` lies on `PR`
So `V` is the foot of the perpendicular from `V` to `PR`
g.
The point `V` is a point on a line through the center of the square and perpendicular to the square.
`VPQRS` is a right, square-based pyramid with `V` as the vertex.
Question 12
The point `P` and `Q` have coordinates `(0, 19, -1)` and `(-6, 26, -11)`, respectively.
The line `L` has vector equation
`r=3i+9j+2k+λ(3i-10j+3k)`
a. Show that the point `P` lies on the line `L`.
b. Find the magnitude of `|vec(PQ)|`.
c. Find the obtuse angle between `PQ` and `L`.
d. Calculate the perpendicular distance from `Q` to the line `L`.
a.
`λ=-1`
`(3 9 2) -1(3 -10 3) =(0 19 -1) =p`
b.
`|vec(PQ)|=|(-6 7 10)| =sqrt(36+49+100)=sqrt(185)`
c.
`(-6 7 10) . (3 -10 3) =sqrt(36+49+100)sqrt(9+100+9) cos theta`
`θ=143.0^o` to `1` decimal place
d.
Foot of perpendicular, `N`, is at `(-3, 29, -4)`
`vec(QN)=(-3, 29, -4)-(-6, 26, -11)`
`vec(QN)=(3, 3, 7)`
`|vec(QN)|=sqrt(9+9+49)=sqrt(67)`
Question 13
The point A and B have coordinates `(7, 1, 6)` and `(10, 5, 1)`, respectively.
a. Write down a vector equation of the line `AB.`
b. The point `P` lies on the line`AB`. The point `Q` has coordinate `(0, -5, 7)`. Given that `PQ` is perpendicular to `AB`, find a vector equation of the line `PQ`.
c. Find the shortest distance from `Q` to `AB`.
a.
`r=vec(OA)+λvec(AB)`
`=(7 1 6) +λ(3 4 -5)`
b.
P lies on AB, so its position vector can be written in the form:
`p=(7 1 6) +λ(3 4 -5)`
`vec(QP)=(7 1 6) +λ(3 4 -5) -(0 -5 7) =(7+3λ 6+4λ -1-5λ)`
`QP`is perpendicular to `AB`, so:
`(7+3λ 6+4λ -1-5λ).(3 4 -5) =0`
`λ=1`
`vec(QP)=(4 2 4)`
This passage through `Q`, so the vector equation of `PQ` is:
`r=vec(OQ)+λvec(QP)`
`r=(0 -5 7) +λ (4 2 4)`
c.
`|(4 2 4)| =sqrt(16+4+16)=6`
Question 14
The line `L_1` has vector equation`r=3i+2j+5k+λ(4i+2j+3k)`.
The point `A(3, p, 5)` and `B(q, 0, 2)`, where `p` and `q` are constant, lie on the line `L_1`.
a. Find the value of `p` and the value of `q`.
The line `L_2` has vector equation `r=3j+k+μ(7i+j+7k)`.
b. Show that `L_2` and `L_1` intersect and find the position vector of the point of intersection.
c. Find the acute angle between `L_2` and `L_1`.
a.
`r=(3 2 5) +λ(4 2 3)`
`λ=0` gives:
`r=(3 2 5) =(3 p 5)`
`p=2` [1]
`r=(3 2 5) -(4 2 3) =(q 0 2 )`
`q=-1`
b.
The lines intersect when:
`(3 2 5) +s(4 2 3) =(0 3 1) +t(7 1 7 )`
`4s-7t=-3` [1]
`2s-t=1` [2]
`3s-7t=-4` [3]
Solve system equations [1] and [2]:
`s=1` and`t=1`
Give the value obtained to [3]:
`3s-7t=3-7=-4`(yes)
So, `s=1` and `t=1` sastify all three equations.
So the lines intersect at the point with position vector:
`(3 2 5) +s(4 2 3) =(3 2 5) +(4 2 3) =(7 4 8)`
c.
`(4 2 3) .(7 1 7) =sqrt(16+4+9)sqrt(49+1+49)cos theta`
`θ=17.9^o` to `1` decimal place.
Question 15
Given that the lines with vector equations
`r=2i+9j+k+λ(i-4j+5k)`
And `r=11i+9j+pk+μ(-i-2j+16k)` intersect at the point `P`, find the value of `p` and the position vector of the point `P`.
`λ+μ=9`
`2λ-μ=0`
Solve system equations:
`λ=3`and `μ=6`
`1+5λ=p+16μ`
`p=-80`
Intersect at the point with position vector
`2i+9j+k+3(i-4j+5k)`
`=5i-3j+16k`
Question 16
Three lines,`L_1, L_2` and`L_3`, have vector equations
`r=16i-4j-6k+λ(-12i+4j+3k)`
`r=16i+28j+15k+μ(8i+8j+5k)`
`r=i+9j+3k+v(4i-12j-8k)`
The 3 points of intersection of these lines form an acute-angled triangle.
For this triangle, find:
a. The position vector of each of the three vertices.
b. The size of each of the interior angles.
c. the length of each side.
a.
First pair:
`-3λ-2μ=0`
`λ-2μ=8`
Solve system equations:
`λ=2`and `μ=-3`
Point of intersection has position vector `16i-4j-6k+2(-12i+4j+3k)=-8i+4j`
b.
The interior angles are the acute angles between lines.
`(-12i+4j+3k).(8i+8j+5k)=sqrt(144+16+9)sqrt(64+64+25)cos theta`
`θ=107.7^o` to `1` decimal place.
Acute angle `= 180^o-θ=72.3^o` to `1` decimal place
Similar to the other two pairs, giving the angle `55.8^o` for the first and the third lines and `51.9^o` for the second and the third lines.
c.
The vector representing any given side is the difference between the position vectors of the endpoints.
`4i-3k-(-8i+4j)=12i-4j-3k`
Length `=sqrt(12^2+(-4)^2+(-3)^2)=sqrt13`
`4i-3k-(12j+5k)=4i-12j-8k`
Length `=sqrt(4^2+(-12)^2+(-8)^2)=4sqrt14`
`-8i+4j-(12j+5k)=-8i-8j-5k`
Length `=sqrt((-8)^2+(-8)^2+(-5)^2)=3sqrt17`
Question 17
The line `L_1` passes through the points `(3, 7, 9)` and `(-1, 3, 4)`.
a. Find a vector equation of the line `L_1`.
b. The line `L_2` has vector equation `r=i+2j+k+μ(3j+2k)`
Show that `L_1` and `L_2` do not intersect.
a.
Direction vector `=3i+7j+9k-(-i+3j+4k)`
`=4i+4j+5k`
`r=3i+7j+9k+λ(4i+4j+5k)`
b.
`1=3+4λ`
`λ=-1/2`
`2+3μ=7+4λ`
`μ=1`
`9+5λ=13/2≠3`
Inconsistent equations. The lines do not intersect.
Question 18
The point `A` has coordinates `(1, 0, 5)` and the point `B` has coordinates `(-1, 2, 9)`.
a. Find the vector `vec(AB)`.
b. Write down a vector equation of the line `AB`.
c. Find the acute angle between the line `AB` and the line `L` with vector equation`r=i+3j+4k+μ(-i-2j+3k)`.
d. Find the point of intersection of the line `AB` and the line `L`.
a.
`vec(AB)=-2i+2j+4k`
b.
`r=-i+2j+9k+λ(-2i+2j+4k)`
c.
`(-2i+2j+4k).(-i-2j+3k)=sqrt(4+4+16)sqrt(1+4+9)cos theta`
`θ=56.9^o` to `1` decimal place.
d.
`-i+2j+9k+λ(-2i+2j+4k)=i+3j+4k+μ(-i-2j+3k)`
`2λ-μ=-2`
`2λ+2μ=1`
Solve system equations:
`μ=1`
Point of intersection has position vector
`i+3j+4k+(-i-2j+3k)`
`=j+7k`
Question 19
The vector equation of the line `L_1` is given by
`(x y z) =(-3 0 8) +t(4 -1 -3)`.
a. Find the vector equation of the line `L_2` that is parallel to `L_1` and which passes through the point `A(5, -3, 2)`.
b. Show that `A(5, -3, 2)` is the foot of the perpendicular from the point `B(4, -7, 2)` to the line `L_2`.
a.
`(x y z) =(5 -3 2) +t(4 -1 -3)`
b.
`vec(BA).d_(L_2)=(5-4 -3-(-7) 2-2) .(4 -1 -3) =(1 4 0) .(4 -1 -3) =1(4)+4(-1)+0(-3)=0`
Question 20
The point `A`, `B` and `C` are position vectors relative to the origin `O`, given by `vec(OA)=(3 1 5)`, `vec(OB)=(0 -1 2)` and `vec(OC)=(1 2 3)`
a. Find a vector equation for the line `L` passing through `A` and `B`.
b. The line through `C`, perpendicular to`L`, meets `L` at the point `N`. Find the exact coordinates of `N`.
a.
`vec(AB)=(0-3 -1-1 2-5) =(-3 -2 -3)`
So `vec(OB)+tvec(AB)=(0 -1 2) +t(-3 -2 -3)`
b.
`vec(ON)=(-3t+3 -2t+1 -3t+5)`
And the `vec(CN)=(-3t+2 -2t-1 -3t+2)`
Since `vec(CN)` is perpendicular to `L`
`(-3t+2)(-3)+(-2t-1)(-2)+(-3t+2)(-3)=0`
`22t-10=0`
So `t=5/11`
`vec(ON)=(3 1 5) +5/11(-3 -2 -3) =1/11(18 1 30)`
Question 1

In the diagram, OABCDEFG is a cuboid in which `OA = 3` units, `OC = 2` units and `OD = 2` units. Unit vectors i, j and k are parallel to OA, OD and OC respectively. M is the midpoint of EF.
a. Find the position vector of M.
The position vector of P is `i + j + 2k`.
b. Calculate angle `PAM`.
c. Find the exact length of the perpendicular from P to the line passing through O and M.
Question 2
The line l has equation`r=i-2j-3k+λ(-i+j+2k)`. The point A and B have position vectors `-2i+2j-k` and `3i-j+k` respectively.
a. Find a unit vector in the direction of `l`.
The line m passes through the points A and B.
b. Find a vector equation for `m`.
c. Determine whether lines `l` and `m` are parallel, intersect or are skew.
Question 3
Relative to the origin`O`, the position vectors of point A, B and C are given by `vec(OA)=(2 3 7)`, `vec(OB)=(3m 1 1)` and `vec(OC)=(4 -m -m(m+1))`
a. It is given that `vec(OA)=vec(OB)`. Find the angle `OAB`.
b. Find the vector equation of the line `AC`.
Question 4
With respect to the origin `O`, the position vectors of the points A and B are given by `vec(OA)=(-2 0 6)` , `vec(OB)=(1 -1 4)`.
a. Find whether or not the vectors `vec(OA)` and `vec(OB)` are perpendicular.
b. Write down the vector `vec(AB)`.
c. Find a vector equation of the line `AB`.
d. The vector equation of the line `L` is given by `r=7i-12j+7k+μ(-3i+10j-5k)`. Show that the lines `AB` and `L` intersect and find the position vector of the point of intersection.
Question 5

The diagram shows a prism, `ABCDEFGH`, with a parallelogram-shaped uniform cross-section.
The point `E` is such that `OE`is the height of the parallelogram. The point `M` is such that `vec(OM)` is parallel to `vec(DC)` and `N` is the midpoint of `DE`. The side `OD` has a length of `5` units. The unit vectors, i j and k are parallel to`vec(OA), vec(OM)` and `vec(OE)`, respectively.
The position vectors of the points `A`, `E`, `C` and `M` are given by `vec(OA)=9i`, `vec(OM)=15j` and `vec(OE)=12k`.
a. Express the vectors `vec(AH)` and `vec(NH)` in term of i, j and k.
b. Use a vector method to find angle `AHN`.
c. Write down a vector equation of the line `AH`.
Question 6
The position vectors of A, B and C relative to an origin O are given by `vec(OA)=(6 3 2)`, `vec(OB)=(2 n -1)` and `vec(OC)=(8 9 0)` , where `n` is constant.
a. Find the value of `n` for which `|vec(AB)|=|vec(CB)|`.
b. In this case, use a scalar product to find angle ABC.
Question 7
a. Given the vector `8i-2j+5k`and `i+2j+pk`are perpendicular, find the value of the constant `p`.
The line `L_1` passes through the point `(-3, 1, 5)` and is parallel to the vector `7i-j+k`.
b. Write down a vector equation of the line `L_1`.
c. The line `L_2` has vector equation `r=i-2j+2k+μ(i+8j-3k)`. Show that `L_1` and `L_2` do not intersect.
Question 8
The origin `O` and the points`A, B` and `C`are such that `OABC` is a rectangle. With respect to `O`, the position vectors of the points `A` and `B` are `-4i+pj-6k` and `-10i-2j-10k`.
a. Find the value of the positive constant `p`.
b. Find a vector equation of the line `AC`.
c. Show that the line `AC` and the line, `L`, with vector equation `r=3i+7j+k+μ(-4i-4j-3k)` intersect and find the position vector of the point of intersection.
d. Find the acute angle between the lines `AC` and `L`.
Question 9
Relative to the origin `O`, the points `A`, `B`, `C` and `D` have position vectors `vec(OA)=4i+2j-k`, `vec (OB)=2i-2j+5k`, `vec(OC)=2j+7k`, `vec(OD)=-6i+22j+9k`
a. Use a scalar product to show that angle `ABC` is a right angle.
b. Show that `vec(AD)=kvec(BC)` where `k` is a constant, and explain what this means.
c. The point `E` is the midpoint of the line `AD`. Find a vector equation of the line `EC`.
Question 10
With respect to the origin `O`, the points `A`, `B`, `C` and `D` have position vectors given by `vec(OA)=-3i+j+8k`, `vec(OB)=-10i+2j+15k`, `vec(OC)=5i-2j-2k`, `vec(OD)=i+6j+10k`
a. Calculate the acute angle between the lines `AB` and `CD`.
b. Prove that the lines `AB` and `CD` intersect.
c. The point `E` has position vector `5i+3j+4k`. Show that the perpendicular distance from `E` to the line `CD` is equal to`sqrt5`.
Question 11
`PQRS` is a rhombus. The coordinates of the vertices `P`, `Q` and `S` are `(9, 2, 4)`, `(-0.5, 6, 6.5)` and `(4.5, -4, -3.5)`, respectively.
a. Find the vector`vec(PQ)` and `vec(PS)`.
b. Find the coordinate of `R`.
c. Show that `PQRS` is in fact a square and find the length of the side of the square.
d. The point `T` is the centre of the square. Find the coordinates of `T`.
The point `V`has coordinates `(5, 17.5, -13.5)`.
e. Find a vector equation of the line `VT`.
f. Verify that `T` is the foot of the perpendicular from `V` to `PR`.
g. Describe the solid `VPQRS`.
Question 12
The point `P` and `Q` have coordinates `(0, 19, -1)` and `(-6, 26, -11)`, respectively.
The line `L` has vector equation
`r=3i+9j+2k+λ(3i-10j+3k)`
a. Show that the point `P` lies on the line `L`.
b. Find the magnitude of `|vec(PQ)|`.
c. Find the obtuse angle between `PQ` and `L`.
d. Calculate the perpendicular distance from `Q` to the line `L`.
Question 13
The point A and B have coordinates `(7, 1, 6)` and `(10, 5, 1)`, respectively.
a. Write down a vector equation of the line `AB.`
b. The point `P` lies on the line`AB`. The point `Q` has coordinate `(0, -5, 7)`. Given that `PQ` is perpendicular to `AB`, find a vector equation of the line `PQ`.
c. Find the shortest distance from `Q` to `AB`.
Question 14
The line `L_1` has vector equation`r=3i+2j+5k+λ(4i+2j+3k)`.
The point `A(3, p, 5)` and `B(q, 0, 2)`, where `p` and `q` are constant, lie on the line `L_1`.
a. Find the value of `p` and the value of `q`.
The line `L_2` has vector equation `r=3j+k+μ(7i+j+7k)`.
b. Show that `L_2` and `L_1` intersect and find the position vector of the point of intersection.
c. Find the acute angle between `L_2` and `L_1`.
Question 15
Given that the lines with vector equations
`r=2i+9j+k+λ(i-4j+5k)`
And `r=11i+9j+pk+μ(-i-2j+16k)` intersect at the point `P`, find the value of `p` and the position vector of the point `P`.
Question 16
Three lines,`L_1, L_2` and`L_3`, have vector equations
`r=16i-4j-6k+λ(-12i+4j+3k)`
`r=16i+28j+15k+μ(8i+8j+5k)`
`r=i+9j+3k+v(4i-12j-8k)`
The 3 points of intersection of these lines form an acute-angled triangle.
For this triangle, find:
a. The position vector of each of the three vertices.
b. The size of each of the interior angles.
c. the length of each side.
Question 17
The line `L_1` passes through the points `(3, 7, 9)` and `(-1, 3, 4)`.
a. Find a vector equation of the line `L_1`.
b. The line `L_2` has vector equation `r=i+2j+k+μ(3j+2k)`
Show that `L_1` and `L_2` do not intersect.
Question 18
The point `A` has coordinates `(1, 0, 5)` and the point `B` has coordinates `(-1, 2, 9)`.
a. Find the vector `vec(AB)`.
b. Write down a vector equation of the line `AB`.
c. Find the acute angle between the line `AB` and the line `L` with vector equation`r=i+3j+4k+μ(-i-2j+3k)`.
d. Find the point of intersection of the line `AB` and the line `L`.
Question 19
The vector equation of the line `L_1` is given by
`(x y z) =(-3 0 8) +t(4 -1 -3)`.
a. Find the vector equation of the line `L_2` that is parallel to `L_1` and which passes through the point `A(5, -3, 2)`.
b. Show that `A(5, -3, 2)` is the foot of the perpendicular from the point `B(4, -7, 2)` to the line `L_2`.
Question 20
The point `A`, `B` and `C` are position vectors relative to the origin `O`, given by `vec(OA)=(3 1 5)`, `vec(OB)=(0 -1 2)` and `vec(OC)=(1 2 3)`
a. Find a vector equation for the line `L` passing through `A` and `B`.
b. The line through `C`, perpendicular to`L`, meets `L` at the point `N`. Find the exact coordinates of `N`.