Differential equations

The variables `x` and `y` satisfy the differential equation `(dy)/dx=x^2e^(y+2x)` and it is given that `y=0` when `x=0`.

Solve the differential equation and obtain an expression for `y` in terms of `x`. 

`(dy)/dx=x^2e^(y+2x)`

`e^-y (dy)/dx=x^2e^(2x)` 

`inte^(-y)(dy)/dxdx=intx^2e^(2x)dx` 

Using integration by parts (twice):

`-e^-y=1/2x^2e^(2x)-int1/2e^(2x)2xdx` 

`-e^-y=1/2x^2e^(2x)-intxe^(2x)dx`

`-e^-y=1/2x^2e^(2x)-[1/2xe^(2x)-int1/2e^(2x)]dx` 

`-e^(-y)=1/2x^2e^(2x)-1/2xe^(2x)+1/4e^(2x)+C`

Using the fact that `y=0` when `x=0`

`-1=0+0+1/4+C`

`C=-5/4` 

`-e^-y=1/2x^2e^(2x)-1/2xe^(2x)+1/4e^(2x)-5/4`  

`e^-y=-1/2x^2e^(2x)+1/2xe^(2x)-1/4e^(2x)+5/4`

`y=(-1/2x^2e^(2x)+1/2xe^(2x)-1/4e^(2x)+5/4)`   

When using integration by parts twice, it is often best to use various types of bracket because you will normally need to embed pairs of brakets within other brackets. In this question, curly brackets are used to separate embedded calculations.

The number of birds, `x`, in a particular area of land is recorded every year for `t` years. `x` is to be modelled as a continuous variable. The rate of change of the number of birds over time is modelled by `(dx)/dt=frac{x(2500-x)}{5000}`

It is given that`x=500` when `t=0`

(a) Find an expression for `x` in term of `t`. 

(b) How many birds does the model suggest there will be in the long term? 

(a)

`(dx)/dt=frac{x(2500-x)}{5000}`

`frac{5000}{x(2500-x)}(dx)/dt=1`

`int(5000)/(x(2500-x))(dx)/dtdt=int1dt` 

Using partial fractions: 

`(5000)/(x(2500-x))=A/x+B/(2500-x)` 

`5000=A(2500-x)+Bx`

Letting `x=0`:

`5000=2500A+0`

`A=2`

Letting `x=2500`:

`5000=0+2500B`

`B=2`

`int(2/x+2/(2500-x))(dx)/dtdt=int1dt` 

`2ln| x |-2ln| 2500-x| =t+C`

`2ln |x/(2500-x)| =t+C` 

Using the fact that `x=500` when `t=0`:

`2ln frac{500}{2000} =C` 

`C=2ln 0.25` 

`2ln |x/(2500-x)| =t+2ln frac{1}{4}`

`2ln |(4x)/(2500-x)| =t` 

`ln |(4x)/(2500-x)| =t/2`

`(4x)/(2500-x)=e^(t/2)` 

`4x=2500e^(t/2)-xe^(t/2)`

`(4+e^(t/x))x=2500e^(t/2)`

`x=frac{2500e^(t/2)}{4+e^(t/x)}` 

(b)

`x=frac{2500e^(t/2)}{4+e^(t/x)} -> (2500)/1=2500` 

Given that `y=2` when `x=0`, solve the differential equation `y^3(dy)/dx=1+y^4` obtaining an expression for `y^4` in terms of `x`. 

`y^3(dy)/dx=1+y^4`

`(y^3)/(1+y^4)(dy)/dx=1`

`int(y^3)/(1+y^4)(dy)/(dx)dx=int1dx` 

`1/4ln (1+y^4) =x+C`

`ln (1+y^4) =4x+B`

`1+y^4=e^(4x+B)=Ce^(4x)` 

Using the fact that `y=2` when `x=0`

`1+16=Ce^0=C` 

`C=17` 

`y^4=17e^(4x)-1`

The gradient of a curve is such that, at the point `(x, y)`, the gradient of the curve is proportional to `xsqrty`. At the point `(3, 4)` the gradient of this curve is `-5`.

(a) Form and solve a differential equation to find the equation of this curve. 

(b) Find the gradient of the curve at the point `(-3, 4)`. 

(a)

`(dy)/dx=kxsqrty`

Using the fact that `(3, 4)` the gradient is `-5`

`-5=3ksqrt4=6k`

`k=-5/6`

`y^(-1/2)(dy)/dx=-5/6x` 

`inty^(-1/2)(dy)/dxdx=int-5/6xdx` 

`2y^(1/2)=-5/12x^2+C`

Using the fact that `y=4` when `x=3`

`4=-45/12+C`

`C=93/12` 

`2y^(1/2)=-5/12x^2+93/12` 

`24sqrty=93-5x^2` 

(b)

`(dy)/dx=-5/6xsqrty` 

At`(-3, 4)`:

`(dy)/dx=-5/6(-3)sqrt4=5`

(a) Given that `x<5`, find `int frac{50}{(5-x)(10-x)}dx`                      

(b) A chemical reaction takes place between two substances A and B. When this happens, a third substance, C, is produced. After `t` hours there are `x-5` grams of A, there are `x-10` grams of B and there are `x` grams of C present. The rate of increase of `x` is proportional to the product of `x-5` and `x-10`. Initially, `x=0` and the rate of increase of `x` is `1` gram per hour.

i. Show that `x` and `t` satisfy the differential equation `50(dx)/dt=(5-x)(10-x)`              

ii. Solve this equation, giving `x` in terms of `t`. 

iii. According to the model, approximately how many grams of chemical C are produced by the reaction? 

(a)

You need to use partial fraction first.

`50/((5-x)(10-x))=A/(5-x)+B/(10-x)` 

`50=A(10-x)+B(5-x)`

Letting `x=10`

`50=0-5B`

`B=-10`

Letting `x=5`

`50=5A`

`A=10`

`50/((5-x)(10-x))=10/(5-x)-10/(10-x)` 

`int 50/((5-x)(10-x))dx=int(10/(5-x)-10/(10-x))dx`

`=-10ln (5-x) +10ln (10-x) +C`

Note that you do not need to use the modulus function because `x<5` and both `5-x` and `10-x` are positive.

(b) i.

`(dy)/dx=k(5-x)(10-x)`

Using the fact that `(dx)/dt=1`when `x=0`

`1=50k`

`k=1/50`

`(dx)/dt=1/50(5-x)(10-x)`

`50(dx)/dt=(5-x)(10-x)` 

ii.

`50/((5-x)(10-x))(dx)/dt=1`

`int50/((5-x)(10-x))(dx)/dtdt=int 1dt`

`-10ln (5-x) +10ln (10-x) =t+C` 

`10ln ((10-x)/(5-x))=t+C` 

Using the fact that `x=0` when `t=0`:

`10ln 2 =c`

`10ln ((10-x)/(5-x))=t+10ln 2`

`10ln ((10-x)/(2(5-x)))=t` 

`(10-x)/(2(5-x))=e^(t/10)`

`10-x=10e^(t/10)-2xe^(t/10)`

`x(2e^(t/10)-1)=10e^(t/10)-10` 

`x=(10(e^(t/10)-1))/(2e^(t/10)-1)` 

iii.

`x=(10(e^(t/10)-1))/(2e^(t/10)-1) ->10/2=5` grams at `t→∞`

The variables x and y are related by the differential equation `(dy)/dx=(xe^x)/(5y^4)`

It is given that `y=4` when `x=0`. Find a particular solution of the differential equation and hence find the value of `y` when `x=3.5`. 

`(dy)/dx=(xe^x)/(5y^4)` 

`5y^4(dy)/(dx)=xe^x`

`int5y^4(dy)/dxdx=int xe^xdx`

Using integration by parts on the right-hand integral:

`y^5=int xe^xdx=xe^x-inte^xdx`

`y^5=xe^x-e^x+C`

Using the fact that `y=4` when `x=0`:

`1024=0-1+C`

`C=1025`

`y=xe^x-e^x+1025`

When `x=3.5`:

`y=root(5)((3.5e^(3.5)-e^(3.5)+1025))=4.06` (to `3` significant figures)

(a) Use the substitution `u=sqrt(y^4-1)` to find `int (y^3)/sqrt(y^4-1)dy`. 

(b) Given that `(dy)/dx=((2x+1)sqrt(y^4-1))/(xy^3)`, `y=sqrt3` when `x=1`, find a relationship between `x` and `y`. 

(a)

`u=sqrt(y^4-1)=(y^4-1)^(1/2)`

`(du)/dy=1/2(y^4-1)^(-1/2) (4y^3)` 

`=(2y^3)/sqrt(y^4-1)`

`int y^3/sqrt(y^4-1)dy=int 1/2(du)/dydy`

`=int 1/2du`

`=1/2u+C`

`=1/2sqrt(y^4-1)+C`

(b)

`(dy)/dx=((2x+1)sqrt(y^4-1))/(xy^3)` 

`y^3/sqrt(y^4-1)(dy)/dx=(2x+1)/x` 

`int(y^3)/sqrt(y4-1)(dy)/dxdx=int(2+1/x)dx` 

`1/2sqrt(y^4-1)=2x+ln|x| +C` 

Using the fact that `y=3` when `x=1`

`1/2sqrt(9-1)=2+ln 1 +C`

`C=sqrt2-2` 

`1/2sqrt(y^4-1)=2x+ln |x| +sqrt2-2`

The height, `h` metres, of a cherry tree is recorded every year for `t` years after it is planted. It is thought that the height of the tree is increasing at a rate proportional to `8-h`. When the tree is planted it is `0.5` metres tall and after `5` years it is `2` metres tall.

(a) Form and solve a differential equation to model this information. Give your answer in the form `h=f(t)`. 

(b) According to the model, what will the height of the cherry tree be when it is fully grown? 

(a)

`(dh)/dt=k(8-h), k>0`

`1/(8-h)(dh)/dt=k`

`int1/(8-h)(dh)/dtdt=intkdt`

`-ln |8-h| =kt+C`

`ln |8-h| =-kt+C'`

`8-h=Ae^(-kt)`

`h=8-Ae^(-kt)` 

Using the fact that `h=0.5` when `t=0`

`0.5=8-Ae^0`

`A=7.5`

`h=8-7.5e^(-kt)` 

Using the fact that`h=2` when`t=5`

`2=8-7.5e^(-5k)`

`e^(-5k)=6/7.5=0.8`

`-5k=ln 0.8`

`k=-1/5ln 0.8` 

`h=8-7.5e^((1/5ln 0.8)t)` 

Note that when multiplying an equation containing an arbitrary constant, you should show that the constant would be modified too. In worked solution a, `c’` is used to show that `c` has changed to a different arbitrary constant.

(b)

Note that `ln0.8`  is negative. Indeed, `lnx` is negative if `x<1`

`e^((1/5ln 0.8) t)→0` as `t→∞`

`h→8` metres 

The variables `x` and `y` satisfy the differential equation `(dy)/dx=e^(3(x+y))`and `y=0` when `x=0`.

Solve the differential equation and obtain an expression for `y` in terms of `x`. 

`(dy)/dx=e^(3(x+y))`

`1/(e^(3y))(dy)/dx=e^(3x)` 

`e^(-3y)(dy)/dx=e^(3x)`

`int e^(-3y)(dy)/dxdx=inte^(3x)dx` 

`-1/3e^(-3y)=1/3e^(3x)+C`

`e^(-3y)=-e^(3x)+C'`

Using the fact that `y=0` when `x=0`

`1=-1+C'`

`C'=2`

`-3y=ln (2-e^(3x))`

`y=-1/3ln (2-e^(3x))`   

At the start of a reaction, there are`x` grams of chemical `X` present. At time `t` seconds after the start, the rate of decrease of `x` is proportional to `xt`.

(a) Using `k` as constant of proportionality, where `k>0`, form a differential equation to model this reaction rate. 

(b) Solve the differential equation obtaining a relation between `x`,`t` and `k`. 

(c) Initially, there are `150` grams of chemical `X` present and after `10` seconds this has decreased to `120` grams. Find the time after the start of the reaction when the amount of chemical `X` has decreased to `1` gram. 

(a)

`(dx)/dt=-kxt` 

(b)

`1/x(dx)/dt=-kt` 

`int1/x(dx)/dtdt=int-ktdt` 

`ln x =(-kt^2)/2+C` 

(c)

Using the result from part b:

`x=Ae^((-kt^2)/2)`

Using the fact that `x=150` when `t=0`

`150=Ae^0`

`x=150e^((-kt^2)/2)` 

Using the fact that `x=120` when`t=10`

`120=150e^(-50k)`

`e^(-50k)=0.8`

`k=-1/50ln 0.8`

`x=150e^((1/100ln 0.8)^(t^2)` 

When `x=1`

`e^((1/100ln 0.8)t^2)=1/150`

`(1/100ln 0.8)t^2=lnfrac{1}{150}`

`t=47.4` s (to `3` significant figures) 

(a) Using partial fractions find `int1/(P(5-P))dP.`

(b) Given that `P=3` when `t=0`, solve the differential equation obtaining an expression for `P` in terms of `t`. 

(c) Describe what happens to`P` when `t→oo`. 

(a)

If you notice that you are going to need partial fractions, then it is best to work them out at the beginning, so that they don’t interrupt the actual solution.

`1/(P(5-P))=A/P+B/(5-P )`

`1=A(5-P)+BP`

Letting `P=0`

`1=5A`

`A=1/5`

Letting `P=5`

`1=0+5B`

`B=1/5` 

`1/(P(5-P))=1/(5P)+1/(5(5-P))` 

`int 1/(P(5-P))dP=int(1/(5P)+1/(5(5-P)))dP`

`=1/5ln|P| -1/5ln |5-P| +C` 

(b)

`(dP)/dt=P(5-P)`

`1/(P(5-P))(dP)/dt=1`

`int1/(P(5-P))(dP)/dtdt= int1dt`

`1/5ln |P| -1/5ln |5-P| =t+C`

Using the fact that `P=3` when`t=0`

`1/5ln |3| -1/5ln |2| =C` 

`1/5ln |P| -1/5ln |5-P| =t+1/5ln |3| -1/5ln |2|`              

`1/5ln ((2P)/(3(5-P))) =t` 

`ln ((2P)/(3(5-P))) =5t`

`(2P)/(3(5-P))=e^(5t)`

`2P=15e^(5t)-3Pe^(5t)`

`P(2+3e^(5t))=15e^(5t)`

`P=(15e^(5t))/(2+3e^(5t))`

(c)

`P=(15e^(5t))/(2+3e^(5t)) ->15/3=5` as `t→∞` 

The population of a country was `50` million in `2000` and `60` million in `2010`. The rate of increase of the population is modelled by `(dP)/dt=(kP(100-P))/100`

Use the model to predict the population of the country in `2025`. 

Note that `P` is the number of millions. So a population of `50` million means that `P=50`.

`100/(P(100-P))(dP)/dt=k`

`100/(P(100-P))=A/P+B/(100-P)`

`100=A(100-P)+BP`

Letting `P=0`

`100=100A`

`A=1` 

Letting `P=100`

`100=100B`

`B=1` 

`(1/P+1/(100-P))(dP)/dt=k`

`int (1/P+1/(100-P))(dP)/dtdt= int kdt`

`ln |P| -ln |100-P| =kt+C` 

Using the fact that`P=60` when`t=0`

`ln 50 -ln 50 =0+C`

`C=0` 

Using the fact that `P=60` when `t=10`

`ln 60 -ln 40 =10k`

`k=1/10ln 1.5` 

`ln |P| -ln |100-P| =1/10ln 1.5 t`

 `ln (P/(100-P)) =(1/10ln 1.5) t`

`P/(100-P)=e^((1/10ln 1.5)t)`

`P=100e^((1/10ln 1.5) t)-Pe^((1/10ln 1.5) t`

`P(1+e^((1/10ln 1.5) t))=100e^((1/10ln 1.5) t)`

`P=frac{100e^((1/10ln 1.5) t)}{1+e^((1/10ln 1.5) t)}` 

When `t=25`

`P=73.4` million (to `3` significant figures) 

(a) Use the substitution `u=x^2` to find `intxsin x^2 dx`. 

(b) Given that `(dy)/dx=frac{xsinx^2}{ y}`, `y=-1` when `x=0`, find a relationship between `x` and `y`. 

(a)

`u=x^2`

`(du)/dx=2x`

`xdx=1/2du`

`intxsin x^2 dx= int1/2sin u du` 

`=-1/2cos u +C` 

`=-1/2cos x^2 +C`

(b)

`(dy)/dx=(xsin x^2)/ y`

`y(dy)/dx=xsin x^2` 

`inty(dy)/dxdx=intxsin x^2 dx` 

`1/2y^2=-1/2cos x^2 +C` 

Using the fact that `y=-1` when `x=0`

`1/2=-1/2+C`

`C=1`

`1/2y^2=-1/2cos x^2 +1`

Solve the differential equation `(dy)/dx=(tan x)/( e^(3y))` given that `x=0` when `y=0`. Give your answer in the form `y=f(x)`. 

`(dy)/dx=(tan x)/ (e^(3y))`

`e^(3y)(dy)/dx=tan x`

`inte^(3y)(dy)/dxdx=inttan x dx` 

`1/3e^(3y)=ln |sec x| +C` 

Using the fact that `y=0` when `x=0`

`1/3=ln 1 +C`

`C=1/3`

`1/3e^(3y)=ln |sec x| +1/3`

`e^(3y)=3ln |sec x| +1` 

`y=1/3ln (3ln x ) +1)`  

`y=1/3ln (1-3ln (cos x) )` 

There are `2000` mice in a field. At time `t` hours, `x` mice are infected with a disease. The rate of increase of the number of mice infected is proportional to the product of the number of mice infected and the number of mice not infected. Initially `500` mice are infected and the disease is spreading at a rate of `50` mice per hour.

(a) Form and solve a differential equation to model this data. Give your answer in the form `t=f(x)`. 

(b) Find how long it takes for`1900` mice to be infected. 

(a)

`(dx)/dt=kx(2000-x)`

Using the fact that`(dx)/dt=50` when `x=500`

`50=500k(1500)`

`k=1/15000` 

`(dx)/dt=1/15000x(2000-x)`

`15000/(x(2000-x))(dx)/dt=1`

`15000/(x(2000-x))=A/x+B/(2000-x)` 

`15000=A(2000-x)+Bx`

Letting `x=0`

`15000=2000A`

`A=15/2`

Letting `x=2000`

`15000=2000B`

`B=15/2`

`(15/(2x)+15/(2(2000-x)))(dx)/dt=1` 

`15/2 int (1/x+1/(2000-x))(dx)/dtdt=int1dt` 

`15/2(ln |x| -ln |2000-x|) =t+C` 

Using the fact that `x=500` when `t=0`

`15/2(ln |500| -ln |1500|) =C`

`C=15/2ln frac{1}{3}` 

`15/2(ln| x| -ln |2000-x|) =t+15/2ln frac{1}{3}`

`t=15/2(ln |x| -ln |2000-x| -ln frac{1}{3})`

`t=15/2ln( (3x)/(2000-x))`

(b)

When `x=1900`

`t==15/2ln ((3(1900))/(2000-1900)) =30.3` hours (to `3` significant figures) 

The variables `x` and `y` are related by the differential equation `x(dy)/dx=1-y^2`

When `x=2, y=0`. Solve the differential equation, obtaining an expression for `y` in terms of `x`. 

`x(dy)/dx=1-y^2`

`1/((1-y)(1+y))(dy)/dx=1/x`

`1/((1-y)(1+y))=A/(1-y)+B/(1+y)` 

`1=A(1+y)+B(1-y)` 

Letting `y=1`

`1=2A`

`A=1/2` 

Letting `y=-1`

`1=2B`

`B=1/2` 

`1/((1-y)(1+y))=1/2(1/(1-y)+1/(1+y))` 

`1/2(1/(1-y)+1/(1+y))(dy)/dx=1/x` 

`int1/2(1/(1-y)+1/(1+y))(dy)/dx dx=int1/x dx`

`1/2(-ln |1-y| +ln |1+y|) =ln |x| +C` 

`1/2ln |(1+y)/(1-y)| =ln |x| +C`

Using the fact that `y=0` when `x=2`

`-1/2ln 1 =ln 2 +C`

`C=-ln 2` 

`1/2ln |(1+y)/(1-y)| =ln |x| -ln 2` 

 `ln sqrt((1+y)/(1-y)) =ln frac{x}{2}`

`sqrt((1+y)/(1-y))=x/2`

`(1+y)/(1-y)=(x^2)/4`

`4+4y=x^2-x^2y`

`y(4+x^2)=x^2-4`

`y=(x^2-4)/(4+x^2)` 

The variables `x` and satisfy the differential equation `(dx)/(dθ)=(x+2)2θ` and it is given that `x=0`when `θ=0`. Solve the differential equation and calculate the value of `x` when `θ=1/4 pi`, giving your answer correct to `3` significant figures. 

Using the fact that `A =1/2-1/2cos 2A`

`(dx)/(d theta)=(x+2)2θ` 

`1/(x+2)(dx)/(d theta)=2θ`

`int 1/(x+2)(dx)/(d theta)dθ= int 2θ dθ` 

`ln |x+2| =int (1/2-1/2cos 4θ) dθ`

`ln |x+2| =1/2θ-1/8sin 4θ +C` 

Using the fact that `x=0` when `θ=0`

`ln 2 =0-0+C`

`C=ln 2` 

`ln |x+2| =1/2θ-1/8sin 4θ +ln 2` 

When `θ=pi/4`

`ln |x+2| =1/2 xx pi/4-1/8sin( 4xx pi/4) +ln 2` 

`x=e^(pi/8+ln 2) -2=0.961` 

The diagram shows an inverted cone filled with liquid paint.

An artist cuts a small hole in the bottom of the cone and the liquid paint drips out at a rate of `16` cm³ per second. At time `t` seconds after the hole is cut, the paint in the cone is an inverted cone of depth `h` cm.

(a) Show that `(dV)/(dh)=4/9 pi h^2`. 

(b) Hence find an expression for `(dh)/dt`. 

(c) Solve the differential equation in part b, giving `t` in terms of `h`. 

(a)

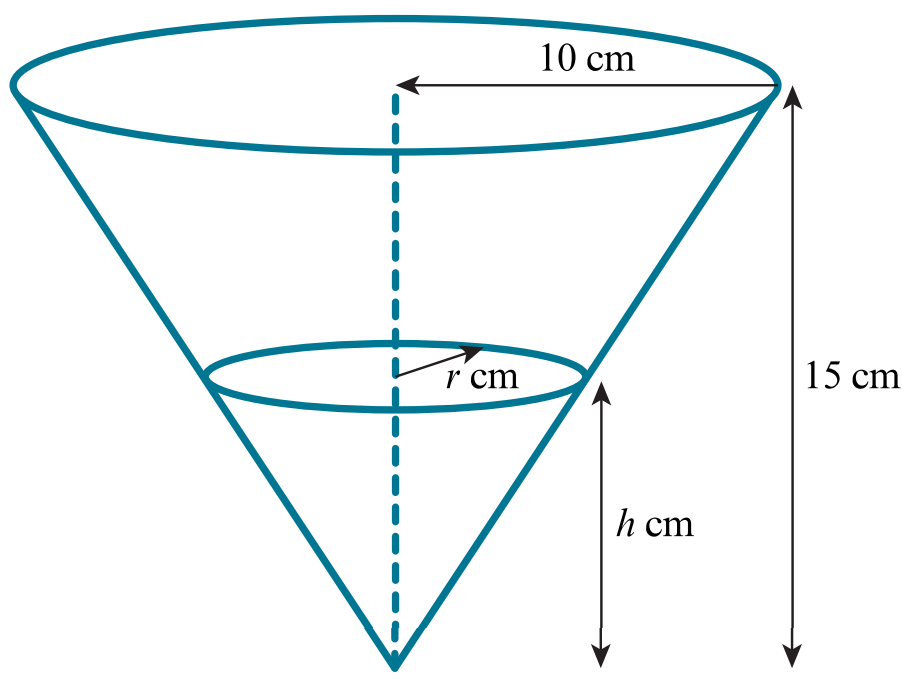
Using similar triangles:

`r/10=h/15` [1]

`r=2/3h`

`V=1/3pir^2h`

`V=1/3pi(2/3h)^2h`

`V=1/3pi(4/9)h^3`

`V=4/27pih^3` [1]

`(dV)/(dh)=4/27 (3πh^2)=4/9pih^2` [1]

Remember that the volume of a right cone with base radius r and height `h` is `1/3pir^2h`.

(b)

Using the chain rule:

`(dV)/(dt)=(dV)/(dh).(dh)/dt` [1]

`-16=4/9pih^2.(dh)/dt`

`(dh)/dt=-144/(4πh^2)=-36/(pih^2)`[1]

(c)

`(dh)/dt=-36/(pih^2 )`

`pih^2(dh)/dt=-36`[1]

`int pih^2(dh)/dtdt=int -36dt`

`1/3pih^3=-36t+C` [1]

`t=-1/36 (1/3pih^3-C)` [1]

Using the fact that `h=15` when `t=0`:

`0=-1/36 (1/3pi15^3-C)`

`C=1/3pi15^3=1125π` [1]

`t=-1/36 (1/3pih^3-1125π)`

`t=pi/36 (1125-h/3)^3` [1]

The size of a population `P`, at time `t` minutes is to be modelled as a continuous variable such that the rate of increase of `P` is directly proportional to `P`.

(a) Write down a differential equation that is satisfied by `P`. 

(b) The initial size of the population is `P_0`. Show that `P=P_0e^(kt)`, where k is a positive constant. 

(c) The size of the population is `1.5P_0` after `2` minutes. Find when the population will be `3P_0`. 

(a)

`(dP)/dt=kP, k>0` 

(b)

`1/P (dP)/dt=k` 

`int 1/P (dP)/dtdt=int kdt` 

`ln P =kt+C`

`P=e^(kt+C)`

`P=A.e^(kt` 

Using the fact that `P=P_0`when `t=0`.

`P_0=Ae^0=A` 

`P=P_0e^(kt)` 

(c)

Using the fact that `P=1.5P_0` when `t=2`:

`1.5P_0=P_0e^(2k)` 

`e^(2k)=1.5`

`2k=ln 1.5`

`k=1/2ln 1.5` 

`P=P_0e^((1/2ln 1.5) t)` 

`P=3P_0` when `3P_0=P_0e^((1/2ln 1.5) t)` 

`e^((1/2ln 1.5) t)=3`

`(1/2ln 1.5)t=ln 3`

`t=(ln 3)/(1/2ln1.5) =5.42` minutes (to `3` significant figures) 

A ball in the shape of a sphere is being filled with air. After `t` seconds, the radius of the ball is `r` cm. The rate of increase of the radius is inversely proportional to the square root of its radius. It is known that when `t=4` the radius is increasing at the rate of `1.4` cm s^-1 and `r=7.84`.

(a) Form a differential equation relating r and t to model this information. 

(b) Solve the differential equation and obtain an expression for `r` in terms of `t`. 

(c) How much air was in the ball at the start? 

(a)

`(dr)/dt=k/sqrtr`

Using the fact that `(dr)/dt=1.4` when `r=7.84`

`1.4=k/sqrt7.84`

`k=1.4sqrt7.84=3.92` 

`(dr)/dt=3.92/sqrtr`

(b)

`(dr)/dt=3.92/sqrtr`

`r^(1/2)(dr)/dt=3.92`

`intr^(1/2)(dr)/dtdt=int3.92dt` 

`2/3r^(3/2)=3.92t+C` 

Using the fact that `r=7.84` when `t=4` 

`2/3 (21.952)=15.68+C` 

`C=-1.045` 

`2/3r^(3/2)=3.92t-1.045`

 `r^(3/2)=5.88t-1.568` 

`r=root(3)((5.88t-1.568)^2)` 

(c)

At the start, `t=0`:

`r=root(3)((0-1.568)^2)` 

`V=4/3pir^3`

`V=4/3pi(0-1.568)^2`

`V=10.3` cm³ (to `3` significant figures)