Complex numbers

The complex number `u` is defined by `u= (3+2i)/(a-5i)`, where `a` is real

(a) Express `u` in the Cartesian form `x + iy`, where `x` and `y` are in terms of `a`. 

(b) Given that `"arg "u = 1/4 pi`, find the value of `a`. 

(a) Multiply numerator and denominator by `a + 5i`, use `i^2 = –1` 

Compare real and imaginary parts: `3 = ax + 5y, 2 = ay - 5x`. 

Obtain answer `(3a-10)/(a^2+25)+ (2a+15)/(a^2+25)i`

(b) State or imply `Im(a) ÷ Re(a) = 1`

 Obtain answer `a = 25` 

Solve the quadratic equation `(3+i)w^2-2w+3-i=0` giving your answers in the form `x + iy`, where `x` and `y` are real. 

Use quadratic formula to solve for `w=(2±sqrt((-2)^2-4(3+i)(3-i)))/(2(3+i))` 

Use `i^2 = -1` in `(3 + i)(3 - i)` 

Obtain one of the answers `w=(2+6i)/(6+2i)` or `w=(2-6i)/(6+2i)`

Show intention to multiply numerator and denominator by conjugate of their denominator.  Independent of previous `M` marks but must be of the same form 

Obtain final answers `3/5+4/5i` and `-i` 

(a) On a sketch of an Argand diagram, shade the region whose points represent complex numbers `z` satisfying the inequalities `|z-4-3i|≤2` and `"Re "z ≤3` 

(b) Find the greatest value of `"arg "z` for points in this region. 

(a)

Show a circle with centre `4+3i`. Accept a curved shape with correct point roughly in the middle. 

Show a circle with radius `2` and centre not at the origin. The shape should be consistent with their scales. 

Show correct vertical line. Enough to meet correct circle twice or complete line for any other circle. 

Shade the correct region on a correct diagram 

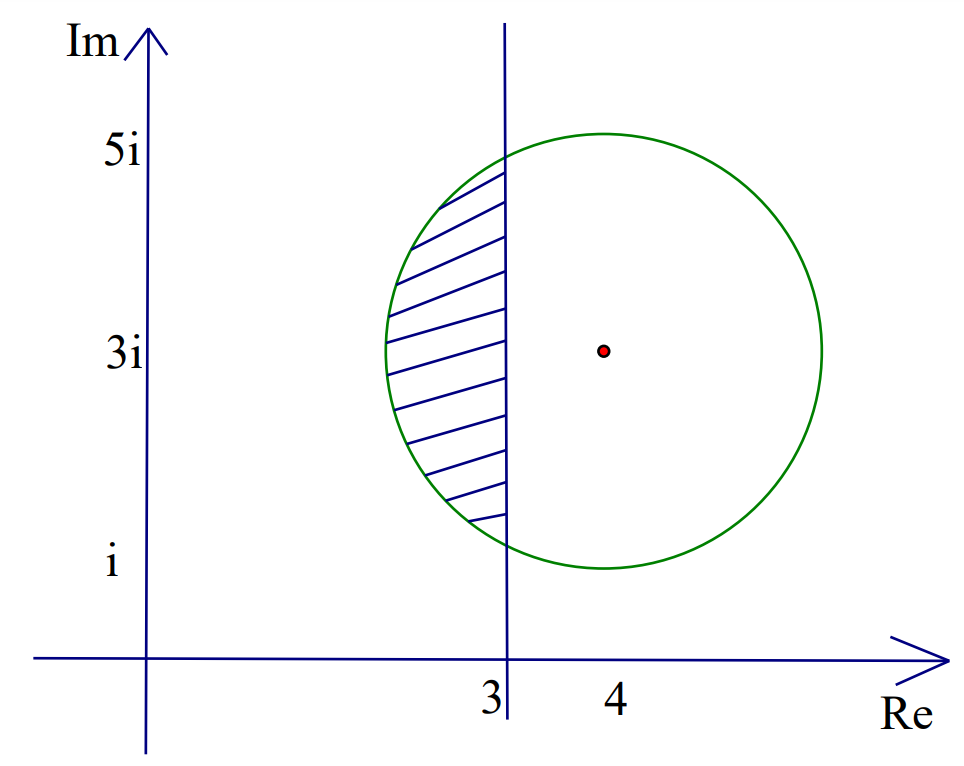
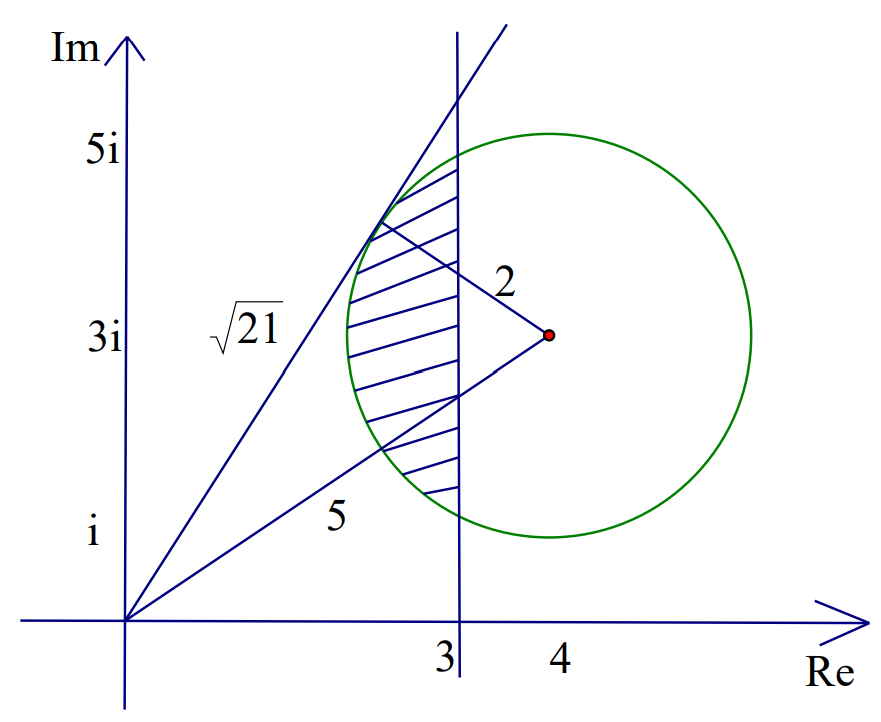
(b)

Carry out a complete method for finding the greatest value of `"arg "(z) : 3/4 + 2/5` 

Obtain answer `1.06` radian 

(a) Express `(5-2i)/(1+3i)`in the form `x+yi` where `x` and `y` are real numbers. 

(b) Solve `w^2-2w+26=0`. 

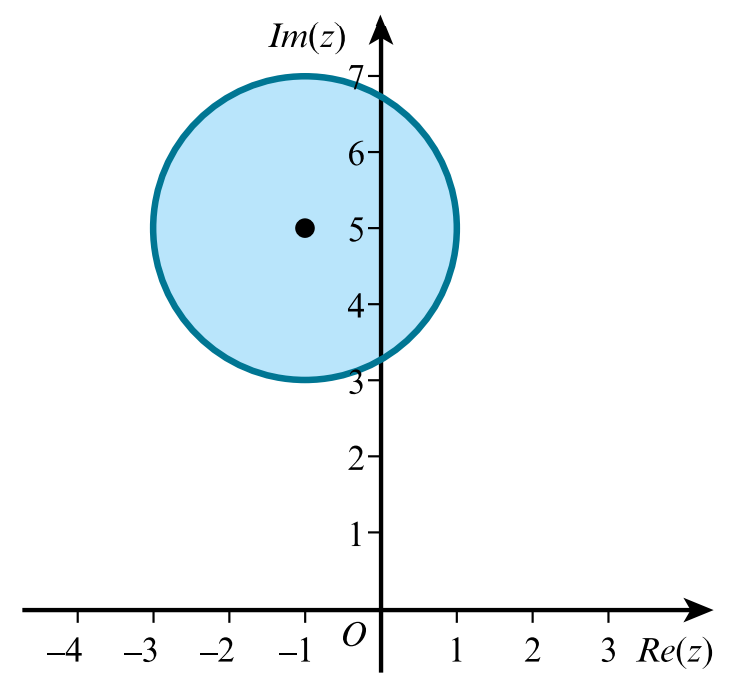
(c) On a sketch of an Argand diagram, shade the region whose points represent complex numbers satisfying the inequality `|z+1-5i|≤2`. 

(a) 

`(5-2i)/(1+3i)`

`=((5-2i)(1-3i))/((1+3i)(1-3i))` 

`=(-1-17i)/(1+9)`

`=-1/10-17/10i`

(b)

`w^2-2w+26=0`

`(w-1)^2-1+26=0`

`(w-1)^2=-25`

`w-1=-+5i` 

`w=1-+5i`

(c)

`|z-(1+5i)|=2` would give a circle, center `(-1, 5)` and radius `2`. 

With the inequality you need the inside of the circle 

(a) Without using calculator, solve the equation: `3w+2iw^**=17+8i` where`w^**` denotes the complex conjugate of `w` . Give your answer in the form `a+bi`. 

(b) In an Argand diagram, the loci: `"arg "(z-2i) =1/6pi` and `|z-3|=|z-3i|` intersect at the point `P`. Express the complex number represented by `P` in the form `re^(iθ)`, giving the exact value of `theta` and the value of `r` correct to `3` significant figures. 

(a) 

`w=a+bi`

`w^**=a-bi`

`3(a+bi)+2i(a-bi)=17+8i` 

Equating real parts:

`3a+2b=17` 

Equating imaginary parts:

`2a+3b=8` 

Solve system equations by substituting method

`a=7, b=-2`

`w=7-2i`

(b)

`arg (z-2i) =1/6 pi`: Half line from `(0, 2)`, with angle `pi/6`

The equation of this half line:

Gradient `= tan frac{pi}{6} =sqrt3/3` 

`y=sqrt3/3x+2, x≥0`

`|z-3|=|z-3i|`: Perpendicular bisector of the point `(0, 3)` and `(3, 0)`.

This is the line with equation `y=x`

The two lines intersect when:

`x=sqrt3/3x+2`

`x=6/(3-sqrt3)`

`y=6/(3-sqrt3)`

So the complex number represented by `P` is: 

`z=6/(3-sqrt3) +6/(3-sqrt3)i`

arg`⁡(6/(3-sqrt3) +6/(3-sqrt3)i)=1=pi/4`

`|6/(3-sqrt3) +6/(3-sqrt3)i|=sqrt((6/(3-sqrt3))^2+(6/(3-sqrt3))^2=6.69` 

`z=6.69e^((iπ)/4)` 

(a) The complex numbers `u` and `v` satisfy the equations `u+2v=2i` and `iu+v=3`. Solve the equations for `u` and `v`, giving both answers in the form `x+yi`, where `x` and `y` are real. 

(b) On an Argand diagram, sketch the locus representing complex numbers `z` satisfying `|z+i|=1` and the locus representing complex numbers `w` satisfying `"arg "(w-2) =3/4 pi`. Find the least value of `|z-w|` for points on these loci. 

() 

`u+2v=2i`

`-> iu=2iv=2i^2`

`iu+2iv=-2` (*)

`iu+v=3` (**)

(**)-(*) 

`v(1-2i)=5`

`v=5/(1-2i)`

`v=(5(1+2i))/((1-2i)(1+2i))` 

`v=(5+10i)/5`

`v=1+2i`

u=2i-2v 

`u=-2-2i` 

(a)

`|z-1|=1`: Circle centre `(0, -1)` radius `1`

`"arg "(w-2) =(3π)/4`: half line from the point `(2, 0)` with angle `(3π)/4` 

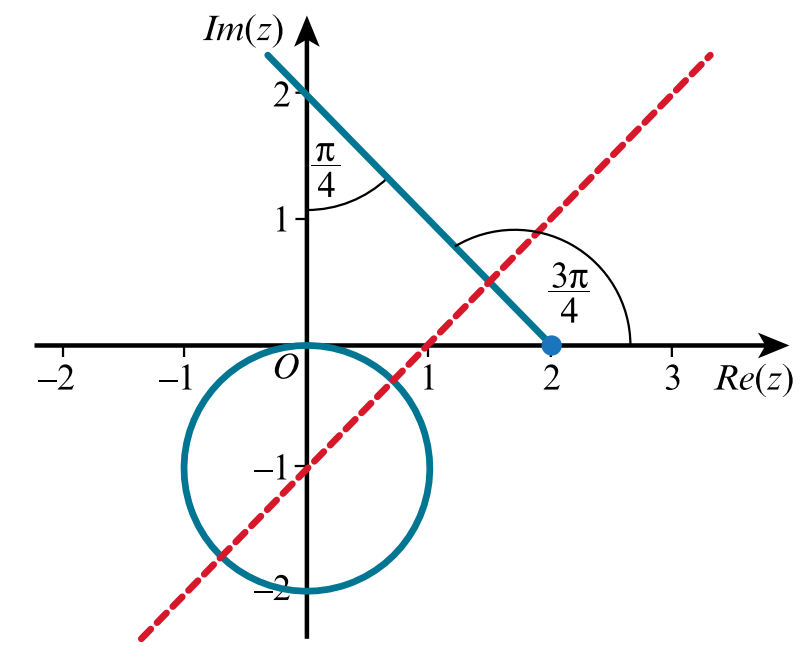
`|z-w|` is the distance between the points representing the complex numbers `z` and `w`. 

The dotted line shows a direction that is perpendicular to the line but passes through the circle. The minimum distance between the half line and circle is the distance between the centre of the circle and the point where the dotted line meets the half line, less the radius of the circle.

`=3sin frac{pi}{4} -1`

`=(3sqrt2)/2-1`

The complex numbers `w` and `z` satisfy the relation `w=(z+i)/(iz+2)`.

(a) Given that `z=1+i`, find `w`, giving your answer in the form `x+yi`, where `x` and `y` are real. 

(b) Given instead `w=z` that and the real part of `z` is negative, find `z`, giving your answer in the form `x+yi`, where `x` and `y` are real. 

(a)

`w=(z+i)/(iz+2)`

`=((1+i)+i)/(i(1+i)+2)` 

`=(1+2i)/(-1+2+i )`

`=(1+2i)/(1+i)`

`=((1+2i)(1-i))/((1+i)(1-i))` 

`=(1+i-2i^2)/(1-i^2)` 

`=(3+i)/2=3/2+1/2i` 

(b)

`z=(z+i)/(iz+2)` 

`iz^2+2z=z+i` 

`iz^2+z-i=0`

Let `z=x+yi`

`i(x+yi)^2+(x+yi)-i=0`

`i(x^2+2xyi+i^2y^2)+x+yi-i=0`

`ix^2+2xyi^2-iy^2+x+yi-i=0`

Equating real parts: 

`-2xy+x=0`

`x(-2y+1)=0`

`x=0` or `(-2y+1)=0` or `y=1/2`

Reap part of `z` is negative, so`x≠0`

So `y=1/2` 

Equating imaginary parts: 

`x^2-y^2+y-1=0`

`x^2-(1/2)^2+(1/2)-1=0`

`x^2=3/4`

`x=-+sqrt3/2`

`x<0`

`x=-sqrt3/2`

So `z=-sqrt3/2+1/2i` 

(a) The complex number`z` is defined as`z=k-6i`, where `k` is the real value. Find and simplify expressions, in terms of `k`, for `zz^**` and `z/z^**`, giving your answers in the form `x+yi` where `x` and `y`are real. 

(b) The complex number `u` and `w` are defined as `u=4(cos frac{5π}{12} +isin frac{5π}{12})` and`w=2e^(iπ)`. Find and simplify expressions for `uw` and `u/w`, giving your answer in the form `re^(iθ)`, where `r>0` and `-π<θ≤π`. 

(a)

`z=k-6i`

`z^**=k+6i`

`zz^**=(k-6i)(k+6i)` 

`=k^2+36` 

`z/z^**=(k-6i)/(k+6i)=((k-6i)(k-6i))/((k+6i)(k-6i))=(k^2-36+12ki)/(k^2+36)`

`=(k^2-36)/(k^2+36)-(12ki)/(k^2+36)`

(b) 

`u=4e^((5iπ)/12)`

`w=2e^(iπ)`

`uw=8e^(iπ(5/12+1))` 

`=8e^(17/12iπ)` 

`=8e^(17/12iπ-2π)` (Notice how subtracting `2` from the argument – pushes the argument back into the correct interval. This doesn’t change the actual complex number, because it is exactly one sweep around the Argand diagram) 

`=8e^(-7/12iπ)`

`u/w=2e^(iπ(5/12-1))` 

`=2e^(-5/12iπ)`

The complex number `w=1+2i`

(a) Represent `w` and `w^**` by points `P` and `Q` on an Argand diagram with origin `O` and describe the polygon `OPQ`. 

(b) Given also that `u=-3-i`, write the complex number `u/w` in the form`r(cos theta +isin theta )`, where `r>0` and `-π<θ≤π`. 

(a)

`w=1+2i`

`w^**=1-2i`

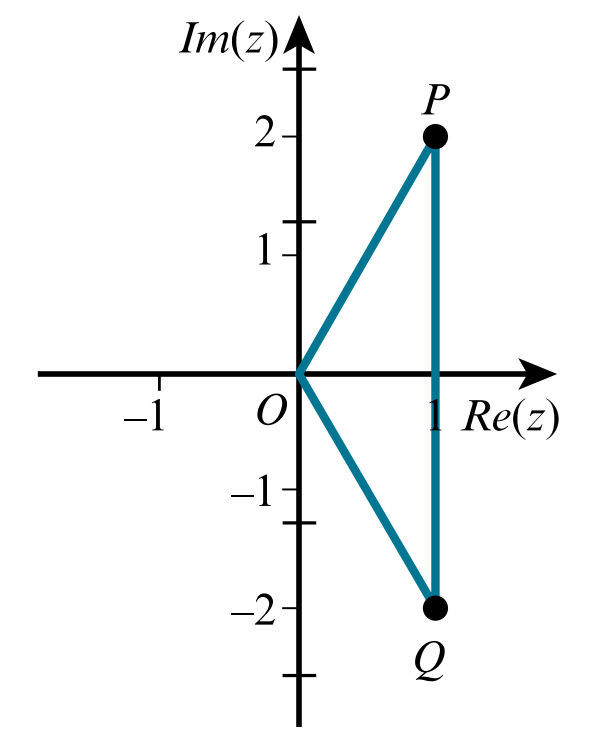
OPQ is an isosceles triangle, because 

`|w|=|w^**|`

(b)

`u/w=(-3-i)/(1+2i)`

`=(-(3+i)(1-2i))/((1+2i)(1-2i))` 

`=(-5+5i)/(1+4)=-1+i`

`|u/w|=sqrt(1^2+1^2)=sqrt2` 

arg `(-1+i)=π-1 =π- pi/4=(3π)/4` 

`u/w=sqrt2(cos frac{3π}{4}+isin frac{3π}{4})`    

`z=2-5i`

(a) Find the real value `x` and `y` such that `z^**=(2x+1)+(4x+y)i` 

(b) On an Argand diagram, show the points `A`, `B` and `C` representing the complex numbers `z`, `z^**`and `-z`. What type of triangle is `ABC`? 

(c) Without using calculator, express `z^**/-z` 

i. in the form `x+yi` where `x` and `y` are real.

ii. in the form `r(cos x +isin x)` , where `r>0` and `-π<θ≤π`.

(a)

`z^**=2+5i`

`2+5i=2x+1+(4x+y)i` 

Equating real parts:

`2x+1=2`

`x=1/2` 

Equating imaginary parts:

`4x+y=5`

`2+y=5`

`y=3`

(b)

`z=2-5i`

`z^**=2+5i`

`-z=-2+5i`

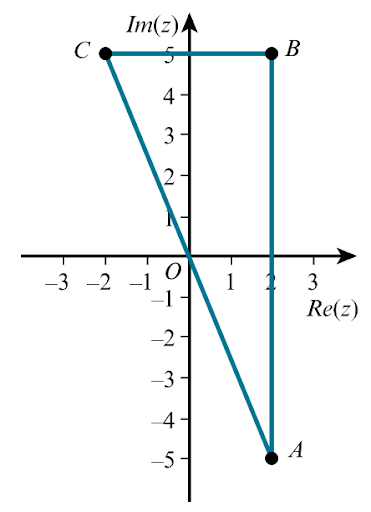
Notice that `-z` is the reflection of `z^**`in the imaginary axis. Also `z` and`z^**` have the same real part, so`z^**` lies vertically above `z` on the Argand diagram. Similarly `z^**`and `-z` have the same imaginary part, so `-z` lies directly to the left of `z^**` on the Argand diagram. Given that the sides joining each of these pairs of points lie, respectively, vertically and horizontally, the triangle must be right-angled. 

(c) i.

`z^**/-z=(2+5i)/(-2+5i)`

`=((2+5i)(-2-5i))/((-2+5i)(-2-5i))` 

`=(-4-20i-25i^2)/(4-25i^2)`

`=(21-20i)/(29)`

`=21/29-20/29i` 

ii.

`|21/29-20/29i|=sqrt((21/29)^2+(20/29)^2)=1` 

arg `(21/29-20/29i) =(20/21)=-0.761` 

`21/29-20/29i=cos (-0.761) +isin (-0.761)` 

`z^2+4sqrt3z+13=0`

(a) Find the roots of this equation, giving your answers in the form `x+yi` where `x` and `y` are real. 

(b) On an Argand diagram with origin `O`, show the position vectors `vec(OA)` and `vec(OB)` representing the roots of the equation. Describe the geometrical relationship between `vec(OA)` and `vec(OB)`. 

(c) Find the modulus and argument of each root. 

(a)

`z^2+4sqrt3z+13=0`

`(z+2sqrt3)^2-12+13=0`

`(z+2sqrt3)^2=-1` 

`z+2sqrt3=-+i`

`z=-2sqrt3-+i` 

(b)

The vector are reflections in the real axis.

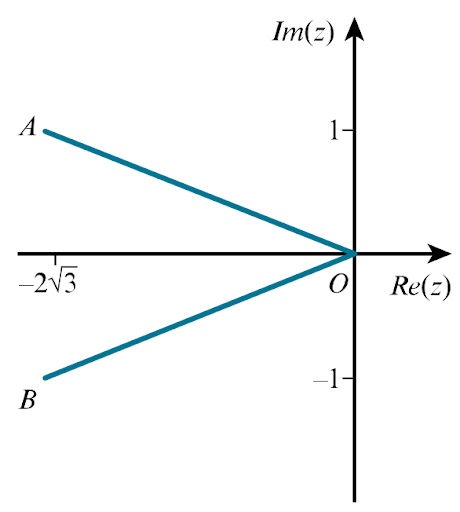
(c)

Two complex conjugates will always have the same modulus.

`z_1=-2sqrt3+i`

`z_2=-2sqrt3-i`

`|z_1|=|z_2|=sqrt((2sqrt3)^2+1^2)=sqrt13`

`"arg "z_1 =π-(1/(2sqrt3)) =2.86` 

`"arg "z_2 =-"arg "z_1 =-2.86` 

`z=4sqrt3-4i`

(a) Find the exact values of the modules and argument of `z`. 

(b) Given that `w=2sqrt2(cos frac{pi}{12}+isin frac{pi}{12})`, write `z/w` in the form `re^(iθ)`, where `r>0` and `-π<θ≤π`. 

(a)

`z=4sqrt3-4i`

`|z|=sqrt((4sqrt3)^2+(-4)^2)=8`

`"arg "z =(-4/(4sqrt3))=-pi/6` 

(b)

`z=8(cos(frac{pi}{-6})+isin (frac{pi}{-6})  =8e^(-(iπ)/6)t` 

`w=2sqrt2(cos frac{pi}{12}+isinfrac{pi}{12})=2sqrt2e^((iπ)/12)` 

`z/w=frac{8e^((-iπ)/6)}{ 2sqrt2e^((iπ)/12)}=2sqrt2e^((-iπ)/6-(iπ)/12)` 

`=2sqrt2e^((-iπ)/4)`

(a) Find the complex number `w` satisfying the equation `w^**-2-2i=3iw`. Give your answer in the form `x+yi`where `x` and `y` are real. 

(b)

i.On a single Argand diagram, sketch the loci `|z-3-3i|=2` and arg `(z-3-3i) =pi/3`. 
ii. Hence determine the value of `z` that satisfies both loci, giving your answer in the form `x+yi`, where `x` and `y` are real. 

(a)

`w^**-2-2i=3iw`

`w=x+yi`

`(x-yi)-2-2i=3i(x+yi)` 

`x-yi-2-2i=3x i-3y`

Equating real parts:

`x-2=-3y`

Equating imaginary parts:

`-y-2=3x` 

Solve the series equations:

`y=1` and `x=-1` 

`w=-1+i` 

(b) i.

`|z-3-3i|=2`: Circle, centre `(3, 3)` and radius `2`. 

arg `(z-3-3i) =pi/3`: half line from `(3, 3)`with angle `pi/3`. 

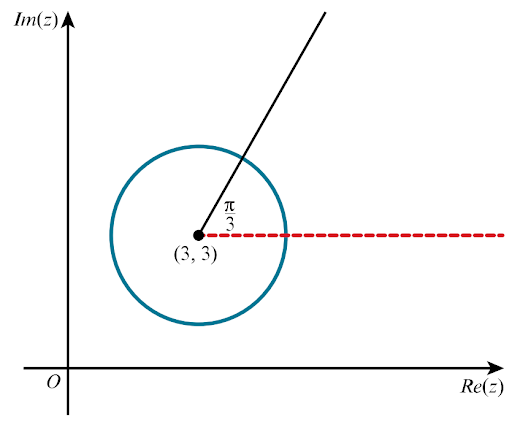
ii.

Half line gradient `= tan frac{pi}{3} =sqrt3`. 

Equation of half line:

`y-3=sqrt3(x-3)`

`y=sqrt3x+3-3sqrt3`

Equation of the circle:

`(x-3)^2+(y-3)^2=4.`

Substituting:

`(x-3)^2+(sqrt3x+3-3sqrt3-3)^2=4`

`x^2-6x+9+3x^2-18x+27=4`

`4x^2-24x+32=0`

`x^2-6x+8=0` 

`(x-4)(x-2)=0`

`x=2` or `x=4` 

Half line, so `x>3`

`x=4`

`y=sqrt3.(4)+3-3sqrt3=3+sqrt3`

`z=4+(3+sqrt3)i`

(a) `(x+yi)^2=7-(6sqrt2)i`

Given that `x` and `y` are real numbers, find the value of `x` and `y`. 

(b) 

i.Show that `z-3` is a factor of `2z^3-4z^2-5z-3`. 
ii. Solve `2z^3-4z^2-5z-3=0`.

(a)

`(x+yi)^2=7-(6sqrt2)i`

`x^2+2xyi+y^2i^2=7-(6sqrt2)i` 

`x^2+2xyi-y^2=7-(6sqrt2)i`

Equating real parts:

`x^2-y^2=7`

Equating imaginary parts:

`2xy=-(6sqrt2)`

`y=-(3sqrt2)/x`

Substituting:

`x^2-(-(3sqrt2)/x)^2=7` 

`x^2-18/x^2=7`

`(x^2)^2-7x^2-18=0`

`(x^2-9)(x^2+2)=0`

`x^2=9` or `x^2=-2` 

`x=3`or `x=-3` (no real roots to `x^2=-2`)

`x=3, y=-sqrt2` 

`x=-3, y=sqrt2` 

(b) i.

`f(z)=2z^3-4z^2-5z-3`

`f(3)=54-36-15-3=0`

`z-3` is a factor of `f(z)` by the factor theorem 

ii.

Dividing `2z^3-4z^2-5z-3`by `z-3` we get `2z^2+2z+1` with the remainder `0` 

`2z^3-4z^2-5z-3= (z-3)(2z^2+2z+1)=0`

`z=3` or `2z^2+2z+1=0`

`z=(-2+-sqrt((2)^2-4(2)(1)))/(2.(2))=(-2+-sqrt(-4))/(4)=(-2+-2i)/4` 

`z=3`; `-1/2+1/2i`;`-1/2-1/2i`

(a) Given that `z_1=5-3i` and `z_1z_2=21+i`, find `z_2`, giving your answer in the form`x+yi`, where `x` and `y` are real. 

(b) Solve `(3z+1)^3=-27` 

(a)

`z_2=(21+i)/(z_1)=(21+i)/(5-3i)=((21+i)(5+3i))/((5-3i)(5+3i))` 

`z_2=(105+68i+3i^2)/(25+9)=(102+68i)/(34)=3+2i` 

(b)

Note: Remember that the complex cube roots of `1` are `1`, `-1/2+(isqrt3)/2`, `-1/2-(isqrt3)/2` 

`(3z+1)^3=-27`

`(3z+1)^3=-3^3`.

`3z+1=-3root(3)1` 

`3z+1=-3.1` or `3z+1=-3.(-1/2+(isqrt3)/2)` or `3z+1=-3.(-1/2-(isqrt3)/2)` 

`z=-4/3` or `z=1/6-sqrt3/2i` or `z=1/6+sqrt3/2i` 

(a) It is given that `w=1` is a root of the equation `f(w)=2w^4+5w^3-2w^2+w-6` 

i. Show that `w+3` is a factor of `2w^4+5w^3-2w^2+w-6`. 

ii. Solve the equation. 

(b) 

i. On an Argand diagram, sketch the locus `|z-1+isqrt3|=1`. 

ii. Write down the minimum value of `"arg "z`. 

iii. Find the maximum value of `"arg "z`. 

(a) i.

`f(w)=2w^4+5w^3-2w^2+w-6`

`f(-3)=162-135-18-3-6=0`

`w+3` is a factor of `f(w)` by the factor theorem 

ii.

The equation gives that `w=1` is a root, so `w-1` is also a factor of `f(w)` by the factor theorem.

`(w+3)(w-1)=w^2+2w-3` is also a factor of `f(w)`

Dividing the equation `2w^4+5w^3-2w^2+w-6`by `w^2+2w-3` we get `2w^2+w+2`with the remainder `0` 

`2w^4+5w^3-2w^2+w-6=0` 

`(w^2+2w-3)( 2w^2+w+2)=0` 

`(w+3)(w-1)( 2w^2+w+2)=0`

`w=-3` or `w=1` 

or `w=(-1+-sqrt(1^2-4(2)(2)))/(2(2))=(-1+-sqrt(15))/4=-1/4+-(isqrt(15))/4` 

(b) i.

Circle, radius `1`, centre `(-1, 3)`

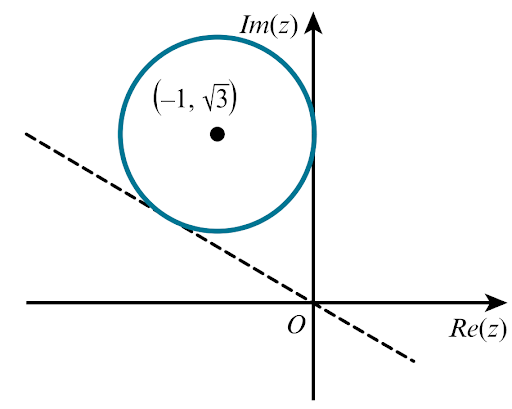
The circle has radius `1` and the x-ordinate of the centre is `-1`. This means that the imaginary axis is a tangent to the circle. 

ii.

Minimum argument occurs when the circle touches the imaginary axis: `"arg "z =pi/2`. 

iii.

Maximum argument occurs when the circle touches the dotted line shown in the diagram. 

Notice that the argument of the complex number at the centre of the circle is `pi/2+1/sqrt3 =pi/2+pi/6`

Given that the centre lies halfway between the imaginary axis and the dotted line, add another `pi/6`. 

So the maximum argument is `pi/2+pi/6+pi/6=(5π)/6`. 

(a)

i. Given that `z_1=-3/2+sqrt7/2i` is a root of the equation `z^2+pz+q=0`, where `q` and `p` are real constants, find the value of `p` and the value of `q`. 

ii. Find `|z_1|`. 

(b)

i. Find the root of the equation `z^3+1=0`. 

ii. On an Argand diagram, show the point A, B and C representing the roots of the equation. What type of triangle is ABC? 

(a) i.

`z=-3/2+sqrt7/2i`

`(-3/2+sqrt7/2i)^2+p(-3/2+sqrt7/2i)+q=0` 

`9/4-(3sqrt7)/2i+7/4i^2-3/2p+psqrt7/2i+q=0`

`9/4-(3sqrt7)/2i-7/4-3/2p+psqrt7/2i+q=0`

Equating real parts:

`1/2-3/2p+q=0`

`2q-3p=-1`

Equating imaginary parts:

`-(3sqrt7)/2+psqrt7/2=0`

`p=3` 

`q=4`

ii.

`|-3/2+sqrt7/2i |`

`=sqrt((-3/2)^2+(sqrt7/2)^2)`

`=sqrt4=2` 

(b) i.

`z^3=-1`

`z=-1` or `z=-1.(-1/2+isqrt3/2)` or `z=-1.(-1/2-isqrt3/2)` 

`z=-1` or `z=1/2-isqrt3/2` or `z=1/2+isqrt3/2`

ii.

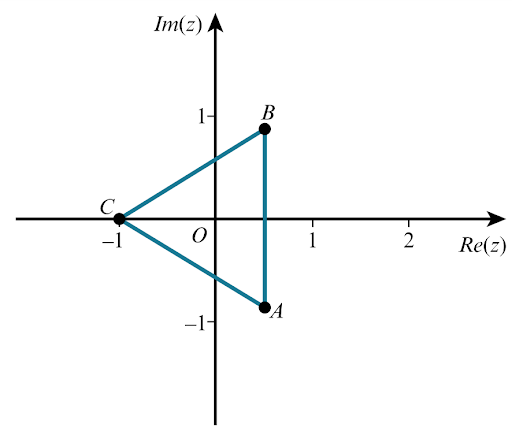
The triangle is equilateral. 

`z=sqrt5-i`

(a) Show that `z/z^**=2/3-sqrt5/3i`. 

(b) Find the value of `|z/z^**|` and `"arg "(z/z^**)` . 

(c) Find and simplify a quadratic equation with integer coefficients that has roots `z/z^**` and its conjugate. 

(a)

`z=sqrt5-i`

`z^**=sqrt5+i`

`z/z^**=(sqrt5-1)/(sqrt5+i)=((sqrt5-1)(sqrt5-1))/((sqrt5+1)(sqrt5-1))`

`=(5-2sqrt5i+i^2)/(5-i^2)=(4-2sqrt5i)/6=2/3-sqrt5/3i` 

(b)

`|2/3-sqrt5/3i|=sqrt((2/3)^2+(-sqrt5/3)^2)=sqrt(4/9+5/9)=1` 

arg `(2/3-sqrt5/3i) =(sqrt(-5))/2 =-0.841`

(c)

Note that if `w` and `w^**` are roots of a polynomial then `(z-w)` and `z-w^**` will both be factors. In turn, `(z-w)(z-w^**)` will also be a factor. 

`[z-(2/3-sqrt5/3i)][z-(2/3+sqrt5/3)i]=0` 

`z^2-(2/3-sqrt5/3i+2/3+sqrt5/3i)z-(2/3-sqrt5/3i)(2/3+sqrt5/3i)=0` 

`z^2-4/3z+(4/9-(5i^2)/9)=0` 

`z^2-4/3z+1=0` 

`3z^2-4z+3=0`

The complex number `z` is defined by `z=(k-4i)/(2k-i)` where `k` is an integer.

(a) The imaginary part of `z` is `"Im "z=7/5`. Find the value of `k`. 

(b) Find the argument of `z`. 

(a)

`(k-4i)/(2k-i)=((k-4i)(2k+i))/((2k-i)(2k+i))=(2k^2-7ki-4i^2)/(4k^2-i^2)` 

`=(2k^2+4-7ki)/(4k^2+1)=(2k^2+4)/(4k^2+1)-(7ki)/(4k^2+1)`  

Equating imaginary parts:

`(-7k)/(4k^2+1)=7/5` 

`-35k=28k^2+7`

`28k^2+35k+7=0`

`4k^2+5k+1=0`

`(4k+1)(k+1)=0`

`k` is an integer, so `k=-1` 

(b)

`z=(-1-4i)/(-2-i)=(1+4i)/(2+i)` 

From part a: `re(z)=(2k^2+4)/(4k^2+1)=6/5` 

`z=6/5+7/5i` 

`"arg "z =7/6 =0.862` 

The complex number `2+2i` is denoted by `u`.

(a) Find the modulus and argument of `u`. 

(b) Sketch an Argand diagram showing the points representing the complex numbers `1`, `i` and `u`. Shade the region whose points represent the complex numbers `z` which satisfy both the inequalities `|z-1|<=|z-i|` and `|z-u|≤1`. 

(c) Using your diagram, calculate the value of `|z|` for the point in this region for which arg `z` is least. 

(a)

`u=2+2i`

`|u|=sqrt(2^2+2^2)=2sqrt2`

arg `u =2/2 = pi/4` 

(b)

`|z-1| <= |z-i|` is the set of all points closer to the point `(1, 0)` than the point `(0, 1)`, i.e. it is the region below the line `y=x`. 

`|z-(2+2i)|≤1` is the inside of a circle, centre `(2, 2)` and radius `1`. 

So shading the part of the circle that lies below the line `y=x`

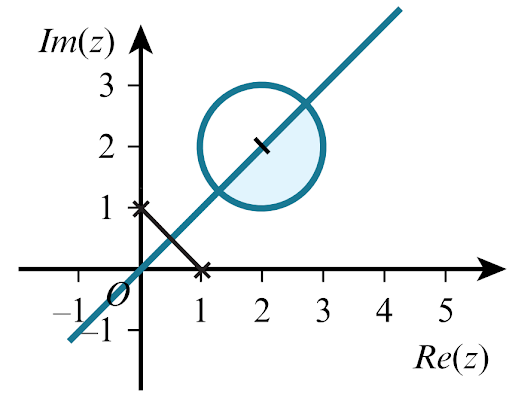
Note that the centre of this circle lies on the perpendicular bisector of `(1, 0)` and `(0, 1)` 

(c)

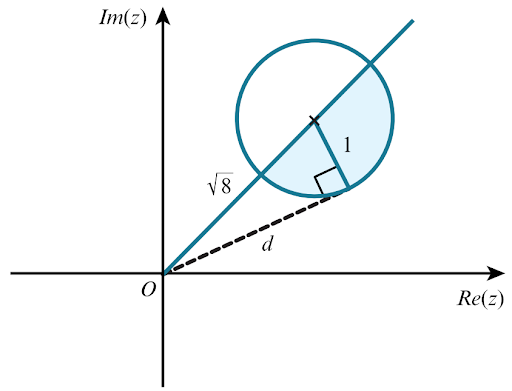
From the diagram, it can be seen that the required modulus is `d`

`d^2=|u|^2-1^2=7` 

`d=sqrt7`