Question 1
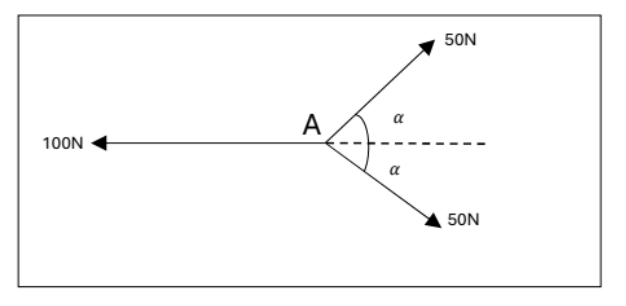
Three coplanar forces of magnitude 100N, 50N and 50 act at a point A, as shown in the diagram.
The value of cosα is `4/5`
Find the magnitude of the resultant of the three forces and state its direction. [3]
Easy
Mark as Complete
Mark Scheme
Question 2
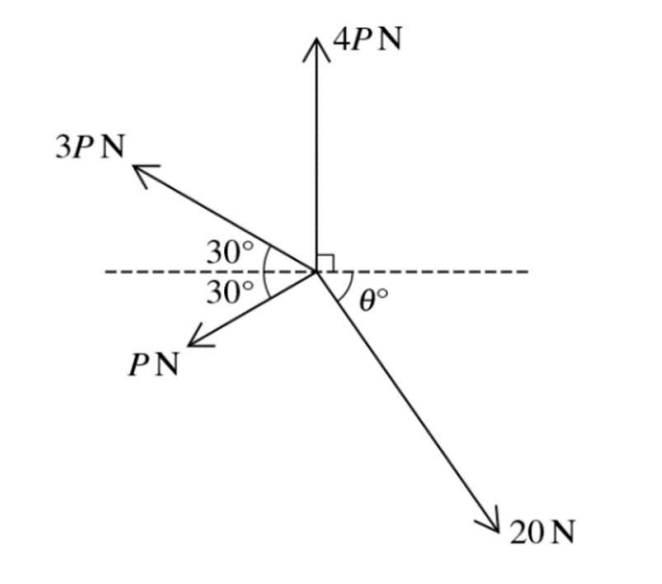
Coplanar forces of magnitudes 20N, P N, 3 P N and 4 P N act at a point in the directions shown in the diagram.
The system is in equilibrium. Find P and `theta` [8]`
Medium
Mark as Complete
Mark Scheme
Question 3
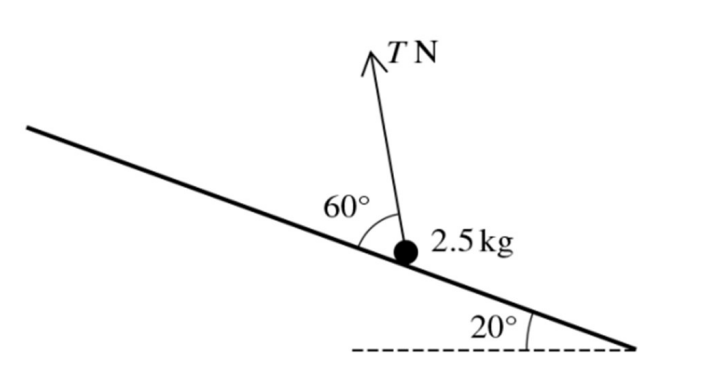
A particle of mass 2.5 kg is held in equilibrium on a rough plane inclined at `20^o` to the horizontal by a force of magnitude T N making an angle of `60^o` with a line of greatest slope of the plane. The coefficient of friction between the particle and the plane is 0.3.
Find the greatest and least possible values of T. [8]
Medium
Mark as Complete
Mark Scheme
Question 4
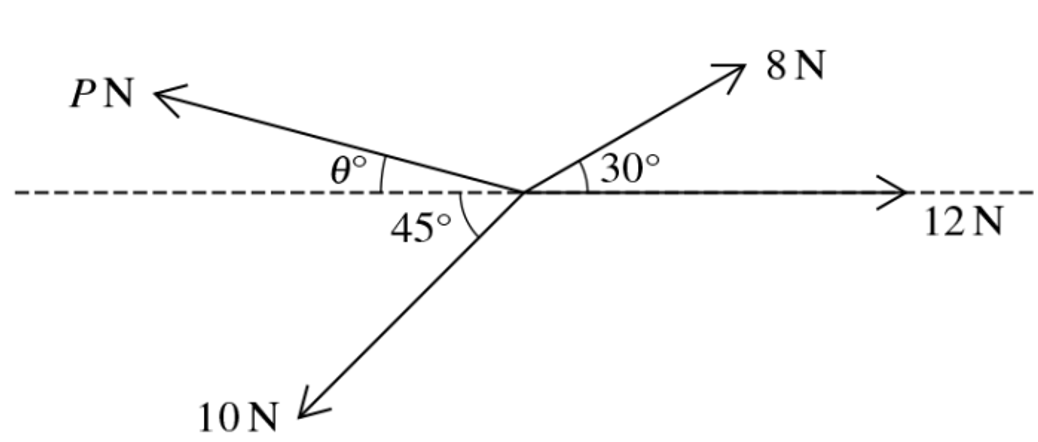
Coplanar forces of magnitudes 8N, 12N, 10N and P N act at a point in the directions shown in the diagram. The system is in equilibrium.
Find P and `theta` [6]
Easy
Mark as Complete
Mark Scheme
Question 5
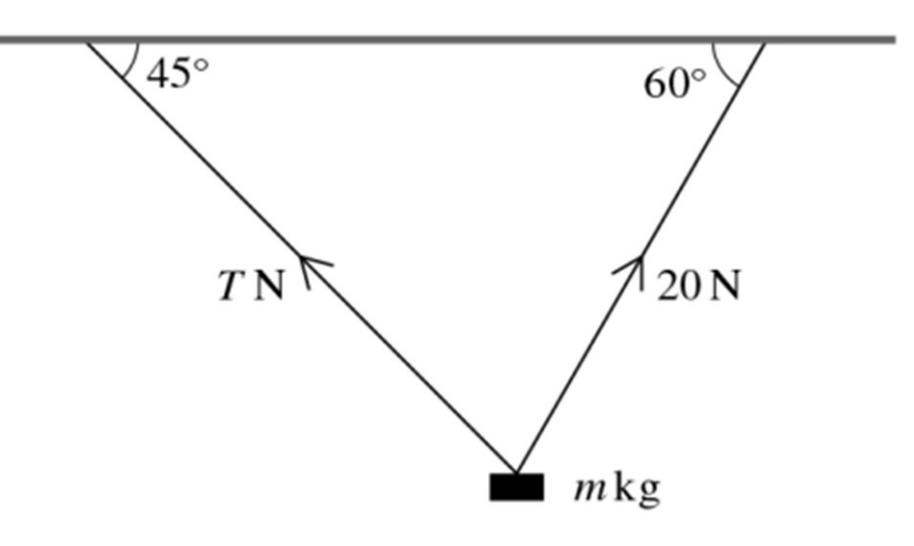
A block of mass m kg is held in equilibrium below a horizontal ceiling by two strings, as shown in the diagram. One of the strings is inclined at `45^o` to the horizontal and the tension is this string is T N. The other string is inclined at `60^o` to the horizontal and the tension in this string is 20N.
Find T and m. [5]
Easy
Mark as Complete
Mark Scheme
Question 6
A string is attached to a block of mass 4kg which rests in limiting equilibrium on a rough horizontal table. The string makes an angle of `24^o` above the horizontal and the tension in the string is 30N.
a. Draw a diagram showing all the forces acting on the block. [1]
b. Find the coefficient of friction between the block and the table. [5]
Medium
Mark as Complete
Mark Scheme
Question 7
A block of weight W N is pulled at a steady speed up a rough plane inclined at an angle of 2`27^o` by a cable of tension T N inclined at an angle of `15^o` to the plane. The reaction and friction force are given by R N and F N, respectively.
a. Draw a diagram showing all the forces acting on the block [1]
b. Given that `F = 1/2R`, so that `T/W`= `frac(cos27 + 2sin27)(2cos15 + sin15)` [6]
Medium
Mark as Complete
Mark Scheme
Question 8
A 20 N particle is held in limiting equilibrium by a horizontal force 14N on a rough slope which is inclined at an angle of `17^o` to the horizontal. The particle is on the point of slipping up the slope.
a. Draw a diagram showing all the forces acting on the particle [1]
b. Calculate the coefficient of friction [3]
Medium
Mark as Complete
Mark Scheme
Question 9
A force of magnitude P N is applied to a particle of weight 60N on a plane inclined at `theta` to the horizontal, where `sintheta = 11/61`. P acts parallel to the plane on a line of greatest slope up the plane. The coefficient of friction between the plane and the particle is 0.12; The particle is in limiting equilibrium.
a. Fill all the forces acting on the particles [1]
b. Find the range of values for P. [5]
Medium
Mark as Complete
Mark Scheme
Question 10
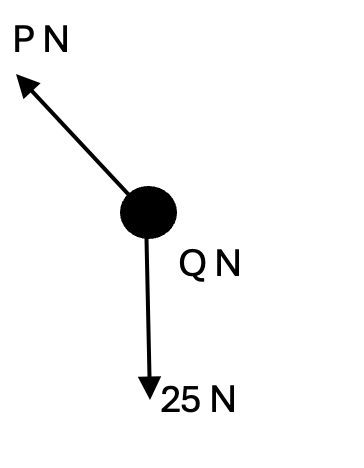
A particle is acted upon by three horizontal forces, P N, Q N and 25 N, as shown in the diagram. The Q N force acts due east and the 25N force acts due south. The P N forces acts on a bearing of`325^o`.
Given that the particle is in equilibrium, find:
a. The value of P. [1]
b. The value of Q. [1]
Easy
Mark as Complete
Mark Scheme
Question 11
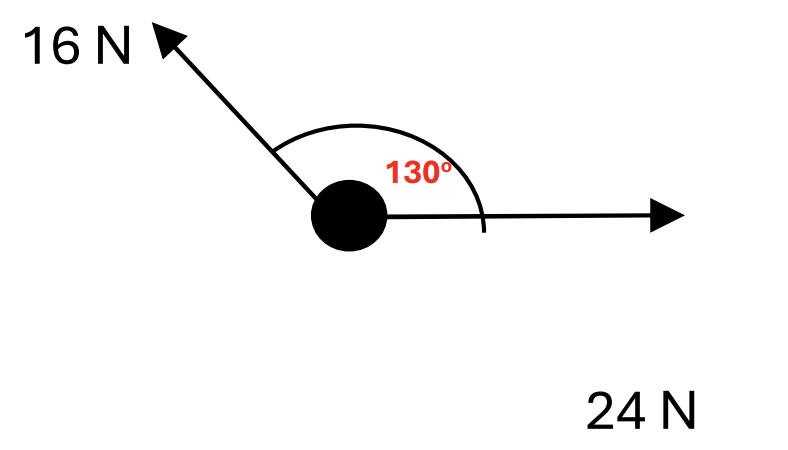
Three forces, F, G and H, act upon a particle in a horizontal plane. Force F has a magnitude of 24 N and acts along the positive x-axis. Force G has a magnitude of 16 N and acts at an angle of `130^o` to the positive x-aixs as shown in the diagram. The three forces are in equilibrium.
a. Find the magnitude of H. [1]
b. Find the angle that H makes with the positive x – axis. [1]
Medium
Mark as Complete
Mark Scheme
Question 12
A book of weight 6 N lies on a smooth plane inclined at to the horizontal, where `tan beta = 3/4`
The book is held in equilibrium by a horizontal force of magnitude G N.
a. Draw all the force act on the book. [1]
b. Calculate the value of G N. [2]
Easy
Mark as Complete
Mark Scheme
Question 13
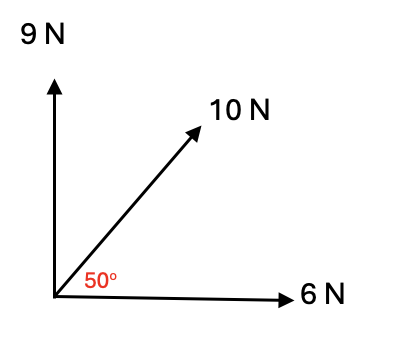
Force J of magnitude 6N acts along Ox (the positive x -axis) and force K of magnitude 9N acts along Oy (the positive y-axis).
Force L of magnitude 10N acts at 50o Ox as shown in the diagram.
Find:
a. The magnitude of the resultant force [2]
The angle the resultant force makes with Ox [2]
Easy
Mark as Complete
Mark Scheme
Question 14
A lawnmower of weight W N sits at rest on a grass slope inclined at an angle of `theta` to the slope. The grass slope is rough and the coefficient of friction betwwen the lawnmower and the grass is `mu`. The lawnmower is on the point of slipping down the grass slope.
a. Show that the tension in the cord is give by `frac(W(mucostheta - sintheta))(musintheta - costheta` [3]
b. Given that the tension is 15N, the weight is 80N and `theta` is 20o, find the value of `mu`. [1]
Medium
Mark as Complete
Mark Scheme
Question 15
A rock of weight W N is about to slip down a rough slopr inclined at an angle of `theta` to the horizontal. The rock is held in position by a horizontal force of magnitude P N, where 5P = W. The coefficient of friction between the rock and the slope is `2/5`.
a. Draw all the force act on the rock. [1]
b. Show that tan`theta` = `37/33` [4]
Medium
Mark as Complete
Mark Scheme
Question 16
A table of weight W N is at rest on a rough plane. A force of P N, parallel to the line of greatest slope of the plane, is applied to the table such that the table is on the point of slipping up the slope. The value of P and the coefficient of friction `mu`,between the table and the plane remain constant when the plane is angled at each of `alpha` and `beta` to the horizontal where sin`alpha` = `3/5` and sin`beta = 8/17`
a. Show that P = `13W/7` [5]
b. Hence show that `mu` = `a/b`, where a and b are coprime and a + b = 19 [1]
Hard
Mark as Complete
Mark Scheme
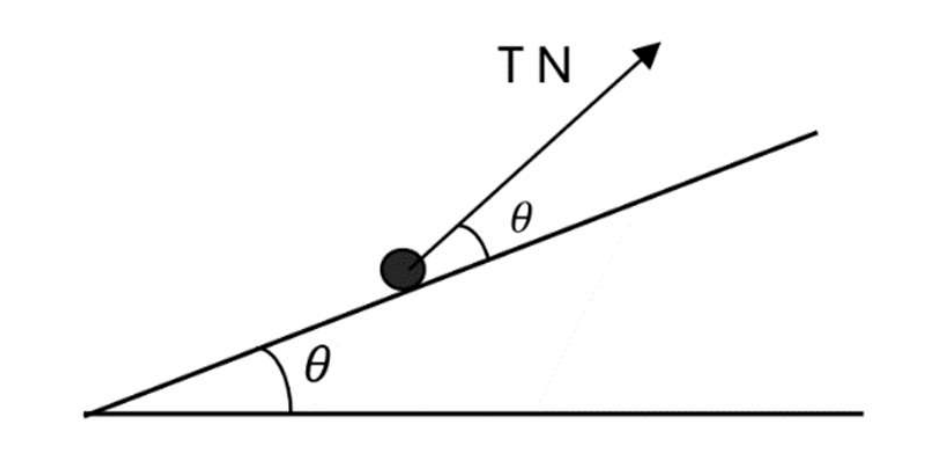
Question 17
Given that tan`alpha = 12/5` and tan`theta = 4/3`, show that the coplanar forces shown in the diagram are in equilibrium.
Easy
Mark as Complete
Mark Scheme
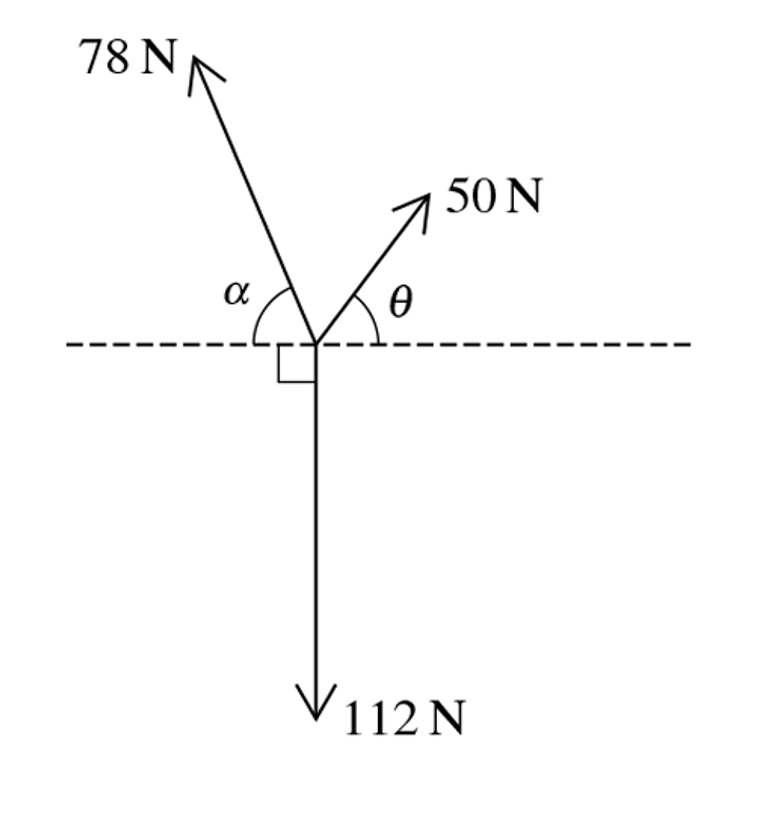
Question 18
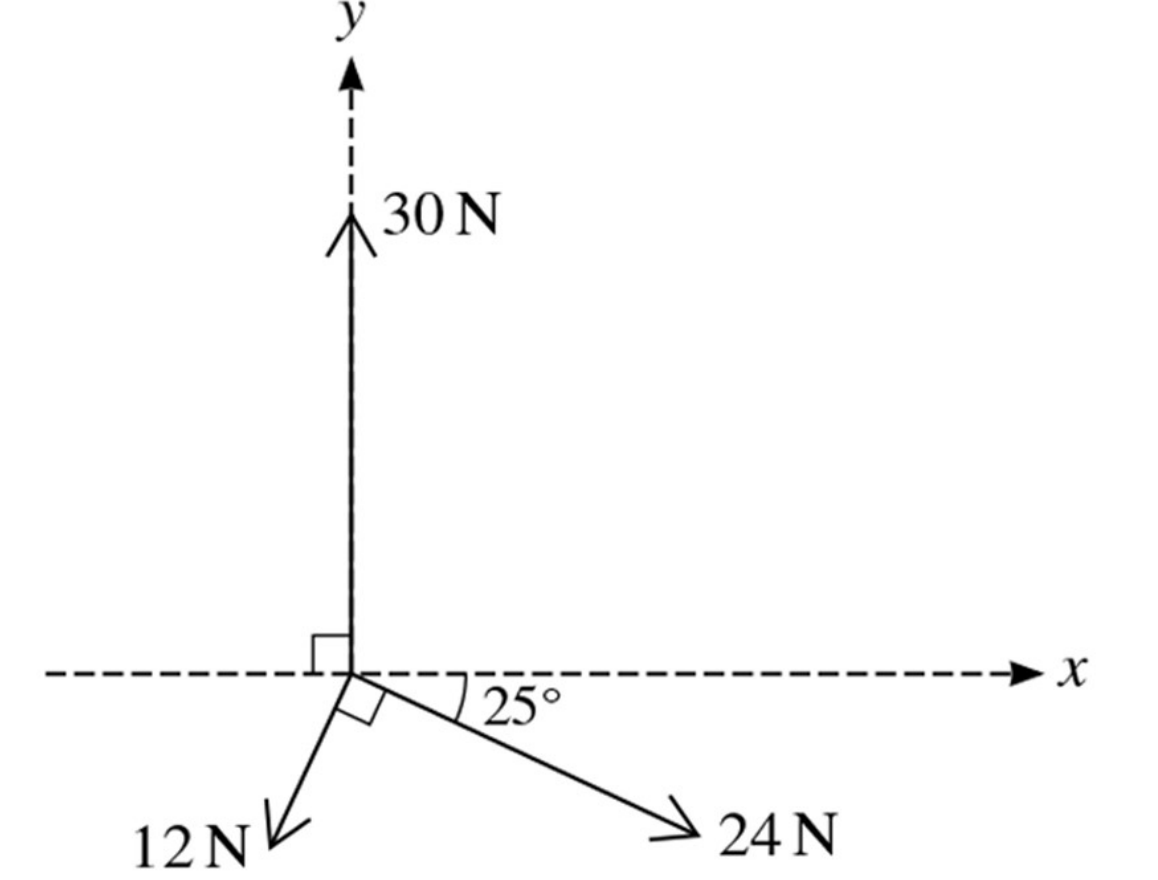
Coplanar forces of magnitudes 12N, 24N and 30N act at a point in the directions shown in the diagram.
a. Find the components of the resultant of the three forces in the x-direction and in the y-direction. [4]
b. Hence find the direction of the resultant. [2]
Medium
Mark as Complete
Mark Scheme
Question 19
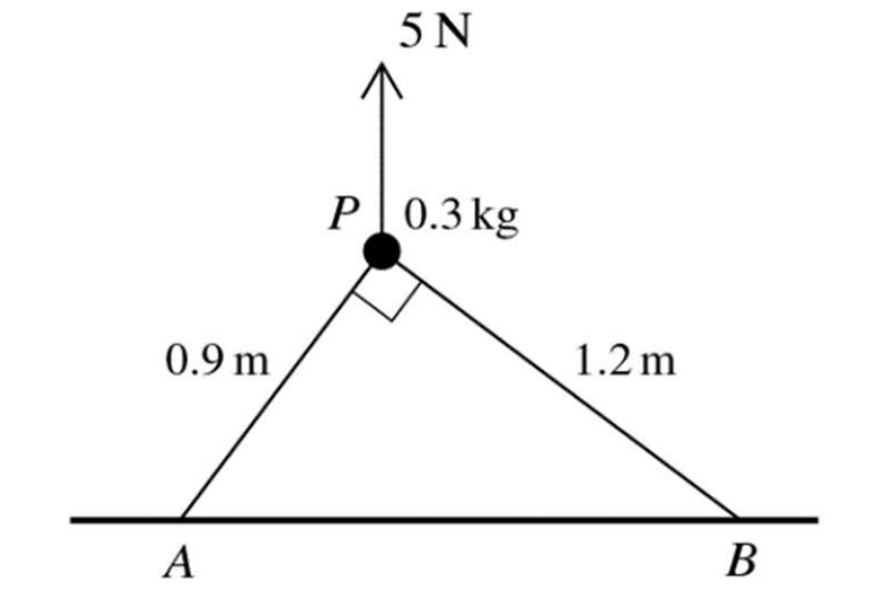
A particle P of mass 0.3kg is held in equilibrium above a horizontal plane by a force of magnitude 5N, acting vertically upwards. The particle is attached to two strings PA and PB of lengths 0.9 m and 1.2 respectively. The points A and B lie on the plane and angle APB = 90o (see diagram).
Find the tension in each of the strings. [5]
Medium
Mark as Complete
Mark Scheme
Question 20
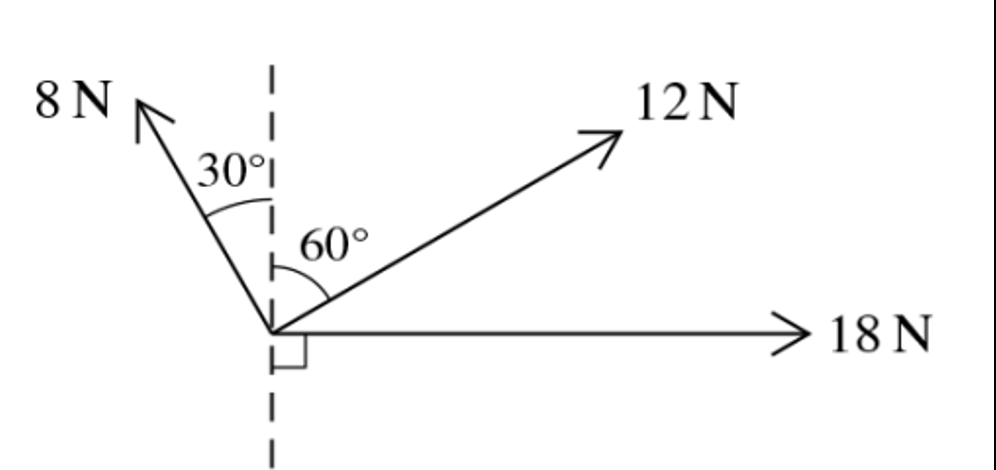
Coplanar forces of magnitude 8N, 12N and 18N act at a point in the direction shown in the diagram.
Find the magnitude and direction of the single additional force acting at the same point which will produce equilibrium. [6]
Medium
Mark as Complete
Mark Scheme
Question 1

Three coplanar forces of magnitude 100N, 50N and 50 act at a point A, as shown in the diagram.
The value of cosα is `4/5`
Find the magnitude of the resultant of the three forces and state its direction. [3]
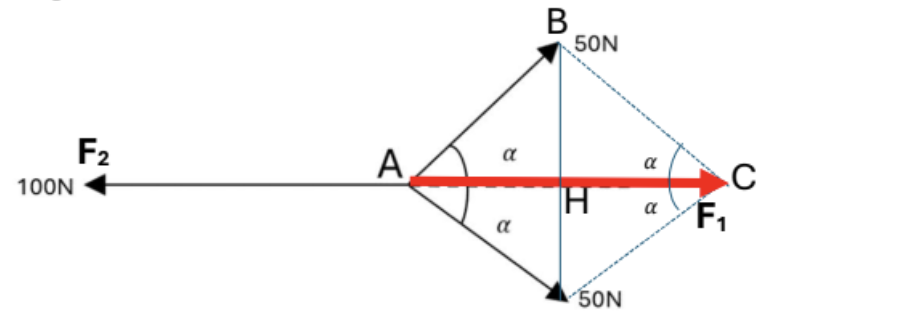
Step 1: Find the `F_1`
Using cosine in right angle triangles (∆ABH)
cosα = `frac(AH)(AB)`
→ AH = 40N.
Because H is the midpoint of AC so AC = F1 = 2.AH = 80N. [1]
Step 2: Find Ft [1]
`vec(F_t) = vec(F_1) + vec(F_2) (vec(F_1) and vec(F_2)` have opposite direction)
so `F_t = 100 - 80 = 20N`
The direction is to the left [1]
Question 2

Coplanar forces of magnitudes 20N, P N, 3 P N and 4 P N act at a point in the directions shown in the diagram.
The system is in equilibrium. Find P and `theta` [8]`
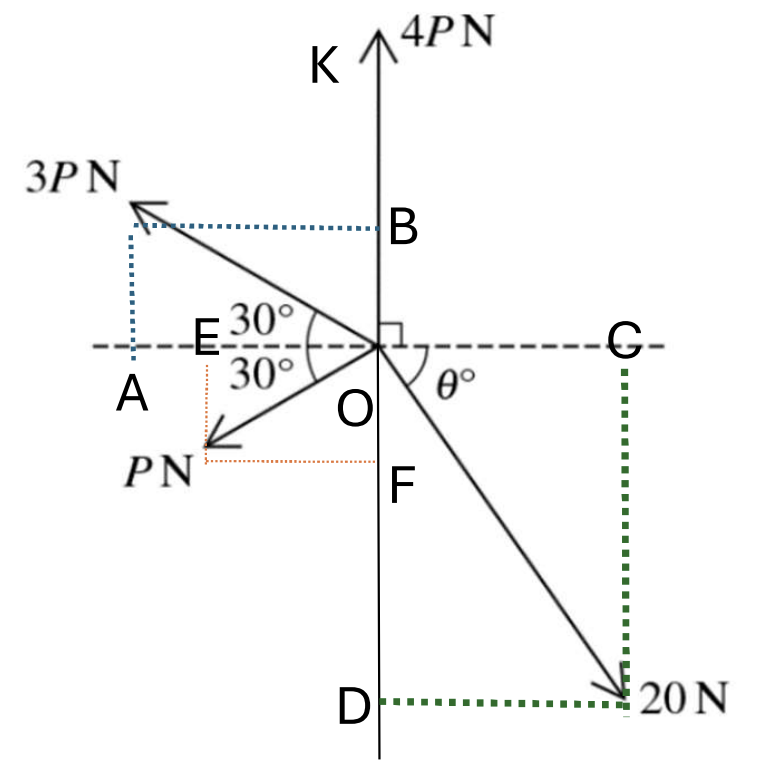
On Ox, we have:
`vec(OA) + vec(OE) + vec(OC) = 0` (system is in equilibrium), choose direction is to the right so [2]
`- OA– OE + OC = 0 `
`to 3PCos30 + Pcos30 = 20costheta`
`to 3Pfrac(sqrt3)(2) + Pfrac(sqrt3)(2) = 20 costheta`
`to 2sqrt3 P = 20costheta` (1) [2]
On Oy, we have:
`vec(OB) + vec(OF) + vec(OD) + vec(OK) = 0`
System is in equilibrium, choose direction goes up so:
OB + OK – OF – OD = 0
`to 3Pcos60 + 4P = 20sintheta + Pcos60`
`to 3P1/2 + 4P = 20sintheta + P1/2`
`to 5P = 20sintheta` (2) [2]
So `sintheta = 1/4P; costheta = frac(sqrt3)(10)P`
`sin^2theta + cos^2theta = 1; (1/4P)^2 + (frac(sqrt3)(10)P)^2 = 1`
So P = 3.29
`theta = 55.3^o` [2]
Question 3

A particle of mass 2.5 kg is held in equilibrium on a rough plane inclined at `20^o` to the horizontal by a force of magnitude T N making an angle of `60^o` with a line of greatest slope of the plane. The coefficient of friction between the particle and the plane is 0.3.
Find the greatest and least possible values of T. [8]
There are two ways to consider:
The friction force is to the left.
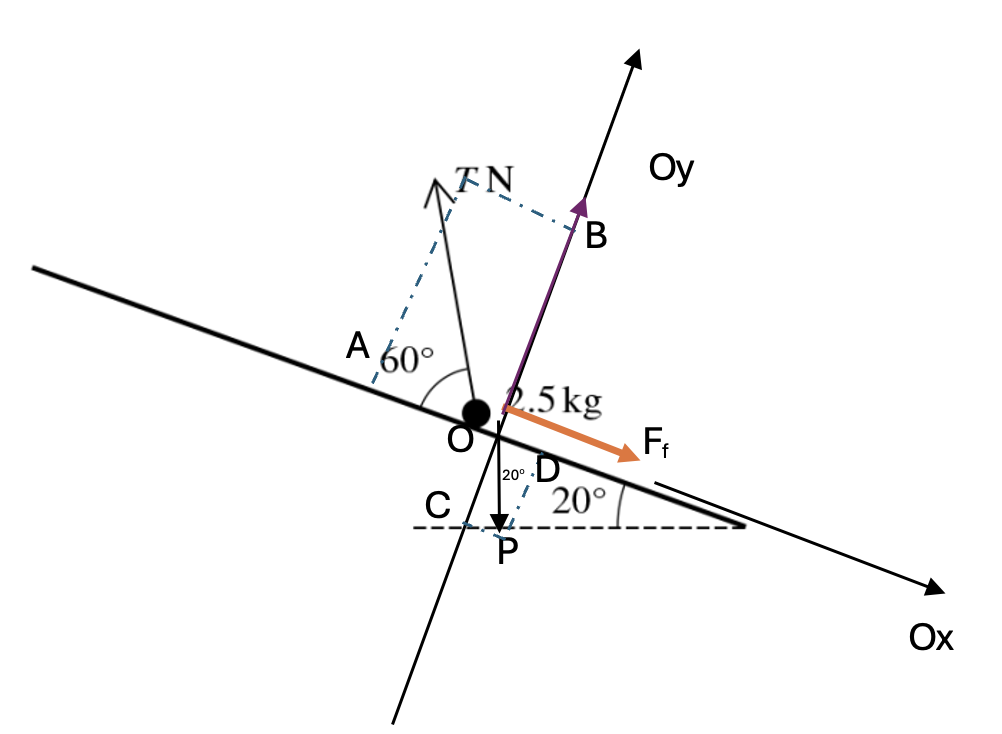
As Ox, we have:
`vec(OA) + vec(OD) + vec(F_f) = 0` (System is in equilibrium), choose direction is to the right so:
-OA + OD + Ff = 0
T.cos60 = 25sin20 + R (1) [1]
As Oy, we have:
`vec(OB) + vec(OC) + vecR = 0` (System is in equilibrium), choose direction goes up so:
OB + R = OC
T.sin60 + R = 25cos20 (2) [1]
Subtitute R = 25 cos20 – Tsin60 in equation (1)
T.cos60 = 25sin20 + 0.3 T = 20.5N [2]
The friction force is to the right.
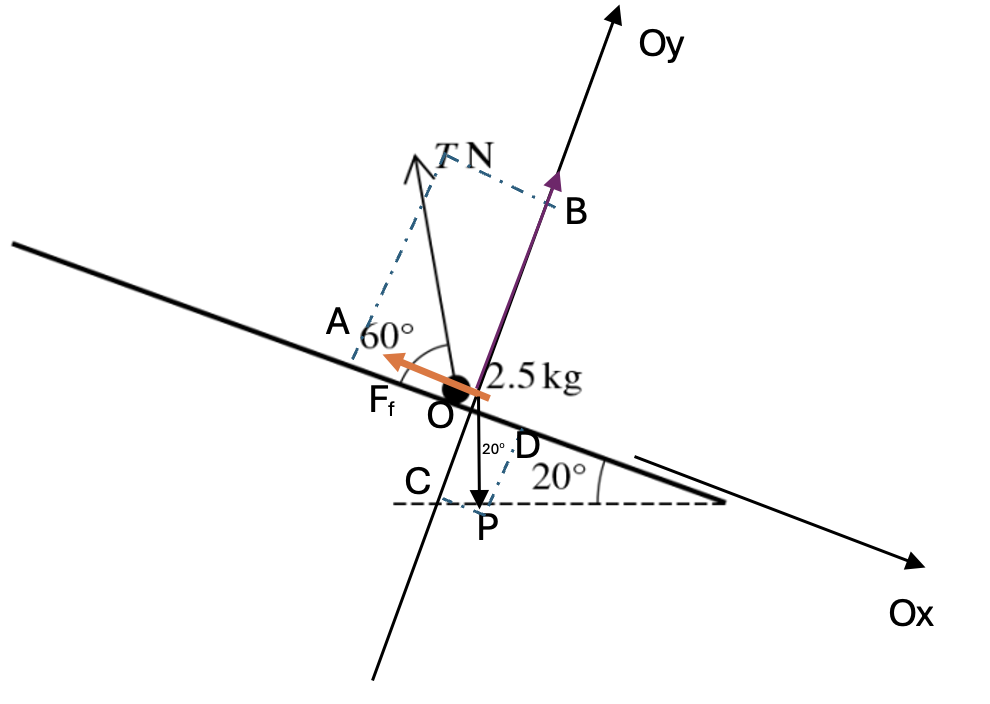
Do the same way as first direction [2]
T.cos60 = 25sin20 - 0.3(25cos20 - Tsin60)
`to` T = 6.26 N [2]
Question 4

Coplanar forces of magnitudes 8N, 12N, 10N and P N act at a point in the directions shown in the diagram. The system is in equilibrium.
Find P and `theta` [6]
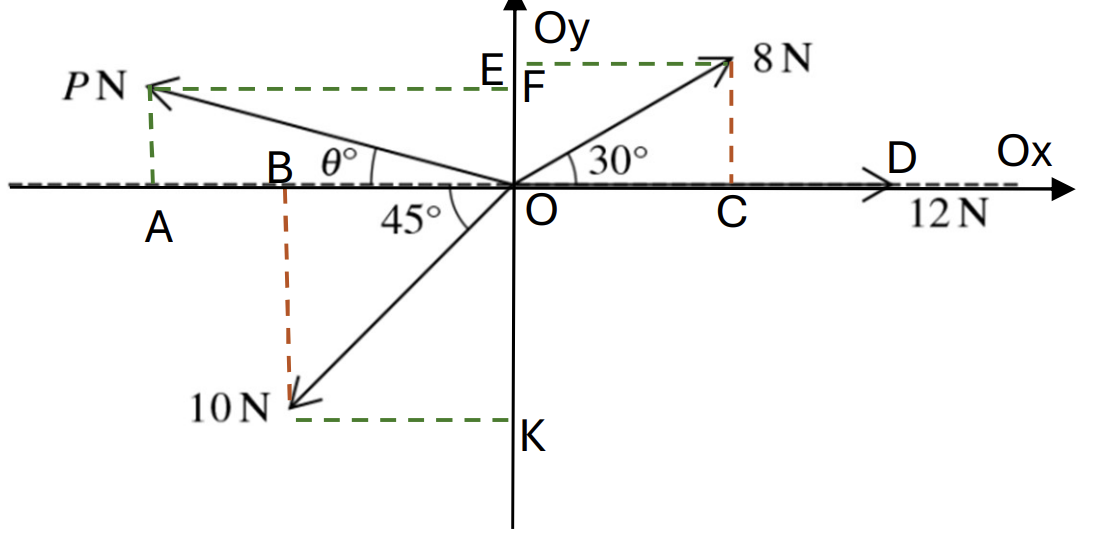
At Ox, find that:
`vec(OA) + vec(OB) + vec(OC) + vec(OD) = 0` (System is in equilibrium), choose direction is to the right so:
`-OA -OB + OC + OD = 0`
`to OC + OD = OA + OB`
`to Pcos θ = 8cos30 + 12 - 10cos45` (1) [2]
At Oy, find that:
`vec(OF) + vec(OE) + vec(OK) = 0` (System is in equilibrium), choose the direction goes up so:
`F + OE – OK = 0`
`to OK = OF + OK`
`to (Pcos θ)^2 + (P sin θ)^2 = (8cos30 + 12 - 10cos45)^2 + (10cos45 - 8sin30)^2``sin θ = 10cos45 - 8sin30 (2) [2]`
`to P = 12.2`
`to theta = 14.5^o` [2]
Question 5

A block of mass m kg is held in equilibrium below a horizontal ceiling by two strings, as shown in the diagram. One of the strings is inclined at `45^o` to the horizontal and the tension is this string is T N. The other string is inclined at `60^o` to the horizontal and the tension in this string is 20N.
Find T and m. [5]
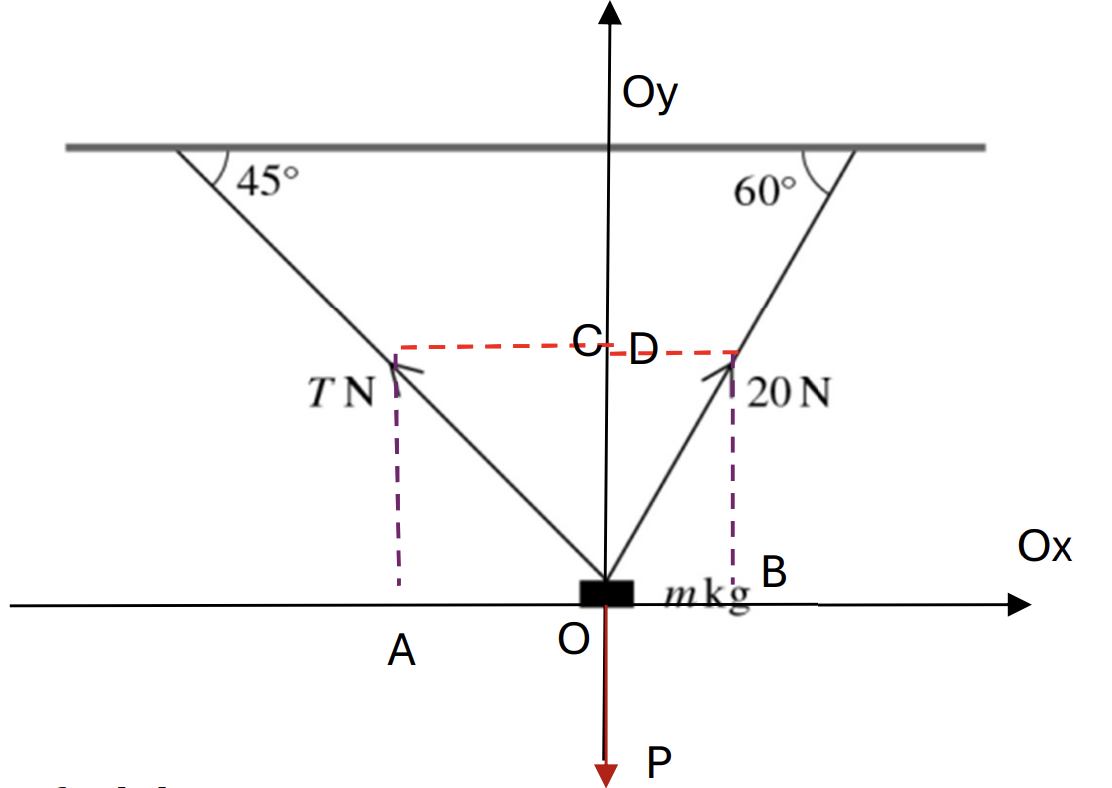
At Ox, find that:
`vec(OA) + vec(OB) = 0` (System is in equilbrium), choose direction is to the right so:
OA = OB
`to Tcos45 = 20cos60 → T = 10sqrt2`
At Oy, find that:
`vec(OC) + vec(OD) + vec(P) = 0` (System is in equilibrium), choose direction goes up so`
OC + OD = P
→ Tcos45 + 20cos30 = mg
→ 10√2cos45 + 20cos30 = 10.m
`→ m = 1 + sqrt3` [2]
Question 6
A string is attached to a block of mass 4kg which rests in limiting equilibrium on a rough horizontal table. The string makes an angle of `24^o` above the horizontal and the tension in the string is 30N.
a. Draw a diagram showing all the forces acting on the block. [1]
b. Find the coefficient of friction between the block and the table. [5]
a. A diagram showing all the forces acting on the block [1]
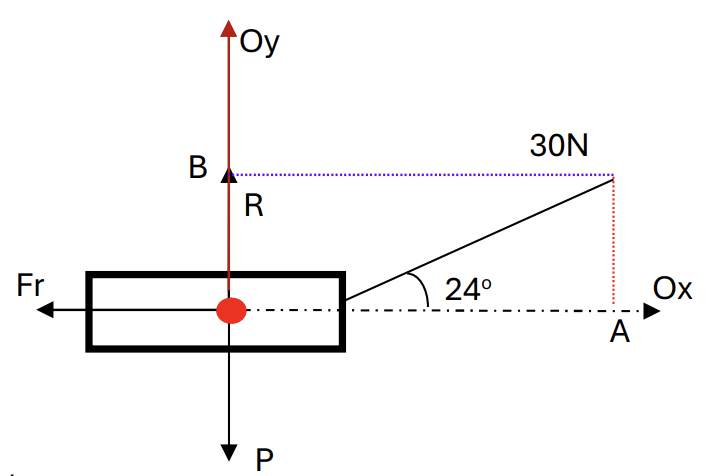
b. At Ox, find that:
`vec(OA) + vec(F_r) = 0` (system is in equilibrium), choose direction is to the right so:
`A = Fr`
`to 30.cos24 = muR` (1)
At Oy, find that:
`vec(OB) + vecR + vecP = 0` (system is in equilibrium), choose direction goes up so:
OB + R = 4.10
`to 30sin24 + R = 40` (2) [2]
`to R = 27.8 N`
`mu = 0.986` [3]
Question 7
A block of weight W N is pulled at a steady speed up a rough plane inclined at an angle of 2`27^o` by a cable of tension T N inclined at an angle of `15^o` to the plane. The reaction and friction force are given by R N and F N, respectively.
a. Draw a diagram showing all the forces acting on the block [1]
b. Given that `F = 1/2R`, so that `T/W`= `frac(cos27 + 2sin27)(2cos15 + sin15)` [6]
a. Draw a diagram showing all the forces acting on the block
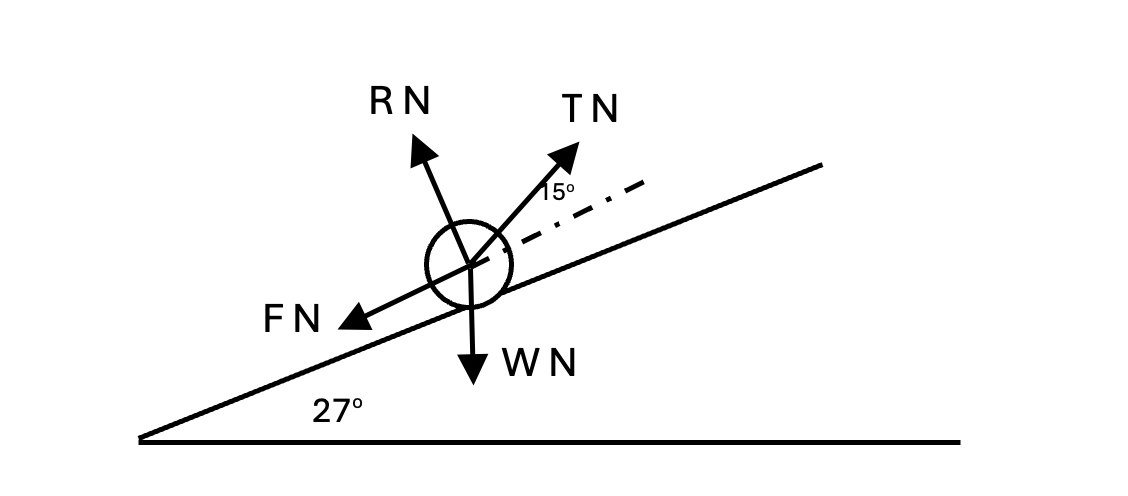
b.
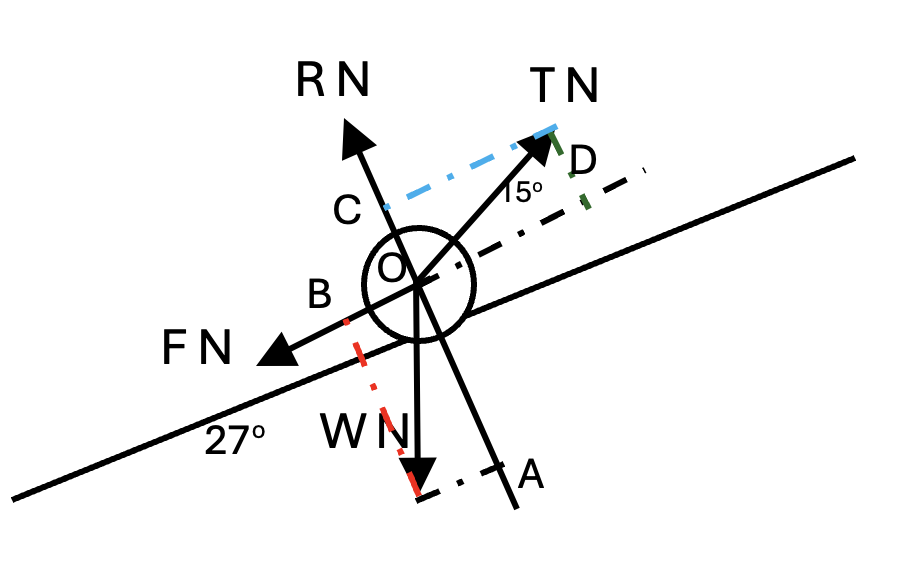
At Ox, find that:
`vec(OB) + vec(OD) + vecF = 0` (system is in equilibrium), choose direction is to the left so:
OB + F = OD
`to Wsin27 + 1/2R= T.cos15` (1) [2]
At Oy, find that:
`vec(OA) + vec (OC) + vecR = 0` (system is in equilibrium), choose direction goes up so:
`C + R = OA`
`to Tsin15 + R = Wcos27` (2) [2]
From two equations, we have:
`{(2Tcos15,-,2Wsin27,=,R),(Wcos27,-,Tsin15,=,R):}`
shown that `T/W = frac(cos27 + 2sin27)(2cos15 + sin15)` [2]
Question 8
A 20 N particle is held in limiting equilibrium by a horizontal force 14N on a rough slope which is inclined at an angle of `17^o` to the horizontal. The particle is on the point of slipping up the slope.
a. Draw a diagram showing all the forces acting on the particle [1]
b. Calculate the coefficient of friction [3]
a.
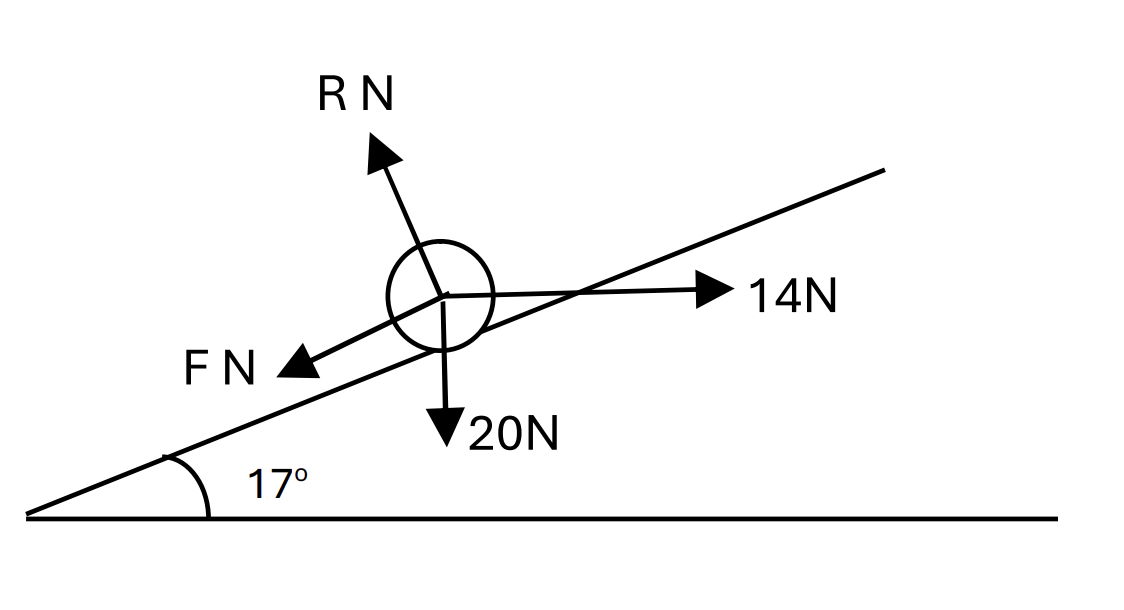
b.
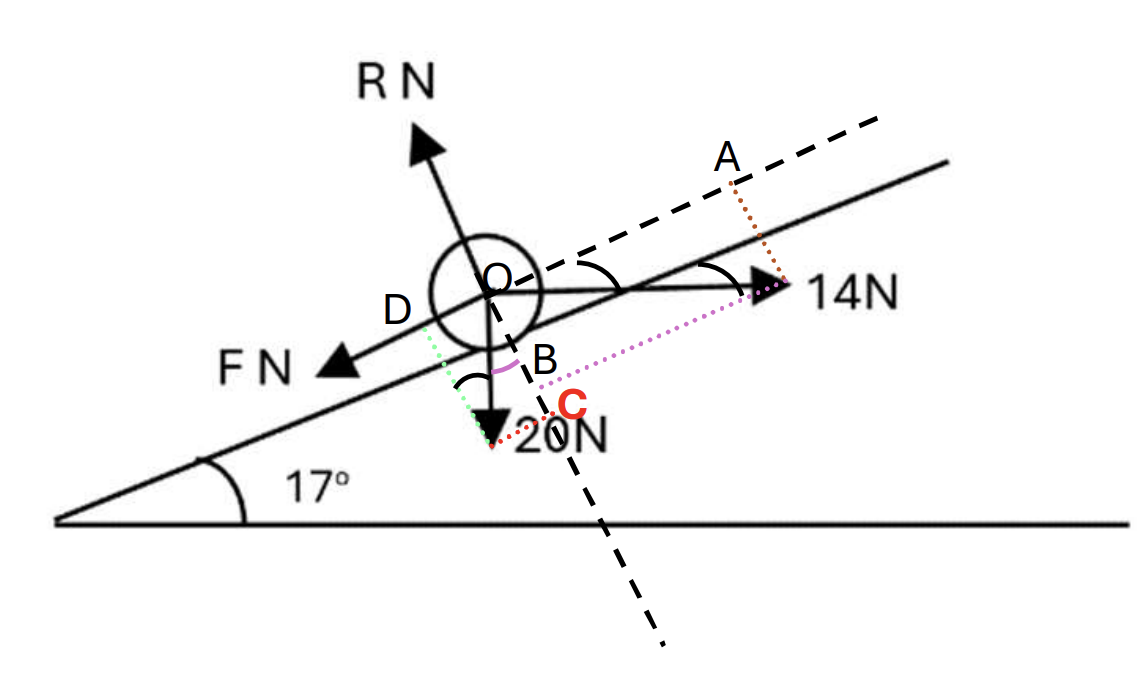
We have horizontal force parallel to horizontal line, so the angle combines between slope and horizontal force equal to `17^o` (corresponding angles).
At Ox, find that:
`vec(OD) + vec(OA) + vecF = 0` (system is in equilibrium), choose direction is to the left so:
OD + F = OA
`to muR = 14cos17 – 20sin17` (1) [1]
At Oy, find that:
`vec(OB) + vec(OC) + vecR = 0` (system is in equilibrium), choose direction goes up so:
R = OC + OB
`R =14cos17 + 20cos17` (2) [1]
Substitute R in equation (1), then R = 14cos17 + 20cos17 [1]
`mu = frac(14cos17 -20sin17)(14cos17 + 20cos17` = 0.325
Question 9
A force of magnitude P N is applied to a particle of weight 60N on a plane inclined at `theta` to the horizontal, where `sintheta = 11/61`. P acts parallel to the plane on a line of greatest slope up the plane. The coefficient of friction between the plane and the particle is 0.12; The particle is in limiting equilibrium.
a. Fill all the forces acting on the particles [1]
b. Find the range of values for P. [5]
a. The frictional force can act either up the plane, when the particle is on the point of slipping down, or up the plane, when the particle is on the point of slipping up.
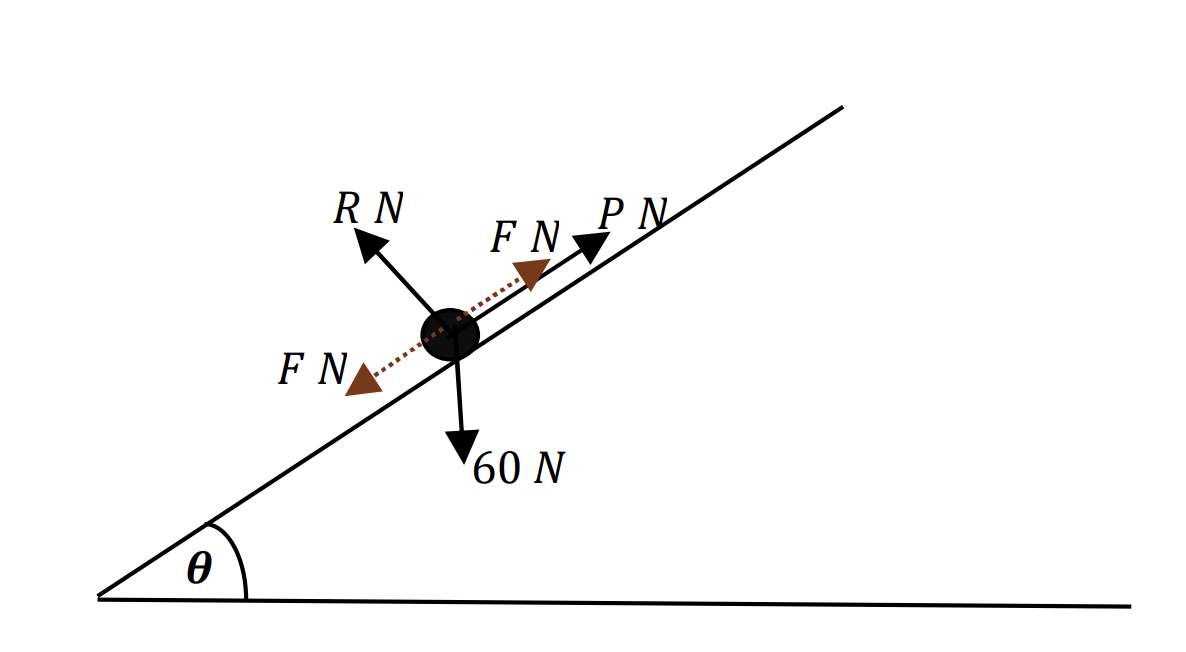
b. The friction force has two directions consist of slipping down and slipping up.
+ Slipping down:
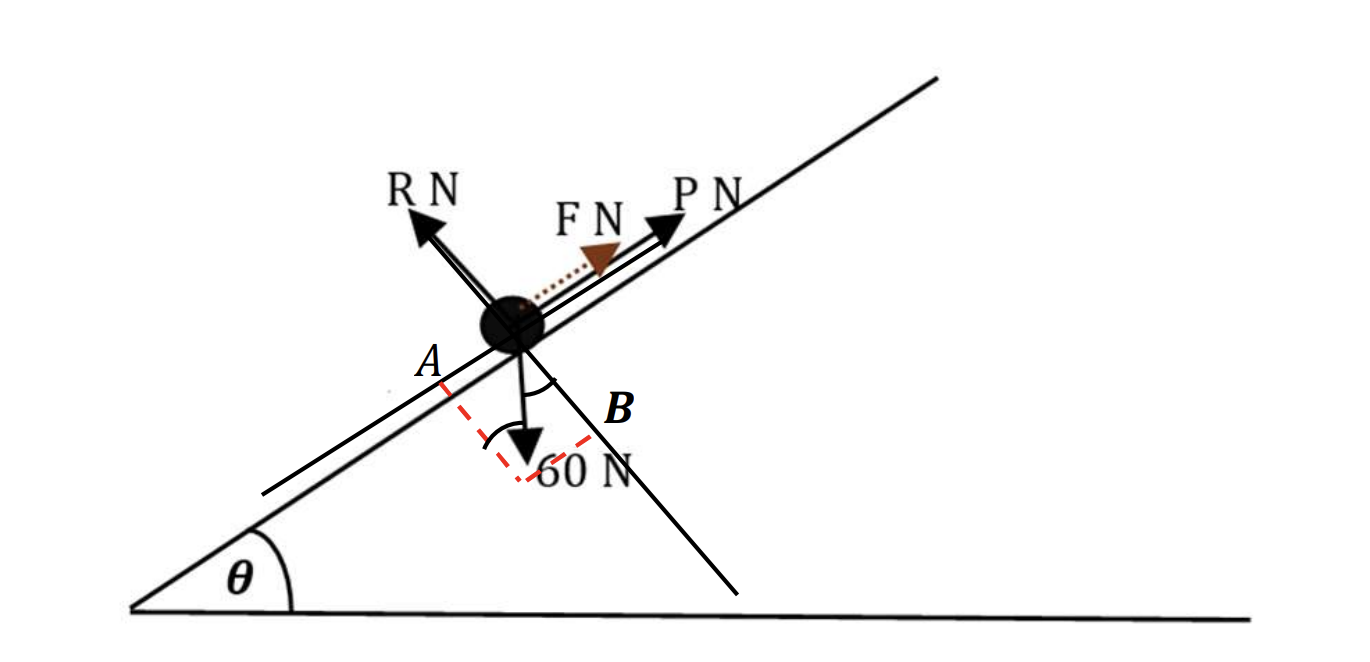
At Ox, find that:
`vec(OA) + vecF + vecP = 0` (system is in equilibrium), choose direction is to the right so:
P + F = OA
`0.12R + P = 60sintheta` (1)
At Oy, find that:
`vec(OB) + vecR = 0` (system is in equilibrium), choose direction goes up so:
R = OB
`to R = 60costheta`
`cos^2 theta+sin^2 theta = 1`
So `costheta = sqrt (1- (11/61)^2) = 60/61`
Substitute `costheta = 60/61` in equation (2)`
R = `60(60/61) = 3600/61` then find P is 3.74 N [2]
+ Slipping up the plane:

Did the same steps as answer above, we got the results: P = 17.9N [2]
Hence the range of values for P is given by 3.74N < P < 17.9N.
Question 10
A particle is acted upon by three horizontal forces, P N, Q N and 25 N, as shown in the diagram. The Q N force acts due east and the 25N force acts due south. The P N forces acts on a bearing of`325^o`.
Given that the particle is in equilibrium, find:
a. The value of P. [1]
b. The value of Q. [1]

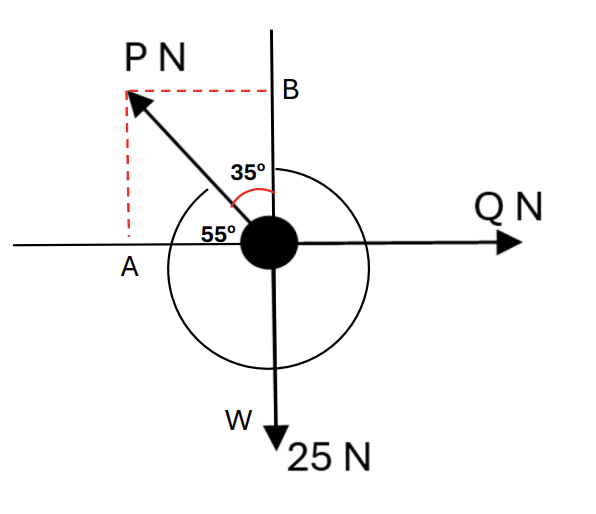
Draw a north line from the point you are measuring the bearing.
At Ox, find that:
`vec(OA) + vecQ = 0` (system is in equilibrium), choose direction is to the right so:
Q = OA
`to Q = Pcos55` (1)
At Oy, find that:
`vec(OB) + vec(W) = 0` (system is in equilibrium), choose direction goes down so:
OB = W
`to Pcos35 = 25` (2)
Then P = `frac(25)(cos35) = 30.52 N` [1]
Q = 30.52 x cos35 = 17.5 N [1]
Question 11
Three forces, F, G and H, act upon a particle in a horizontal plane. Force F has a magnitude of 24 N and acts along the positive x-axis. Force G has a magnitude of 16 N and acts at an angle of `130^o` to the positive x-aixs as shown in the diagram. The three forces are in equilibrium.
a. Find the magnitude of H. [1]
b. Find the angle that H makes with the positive x – axis. [1]

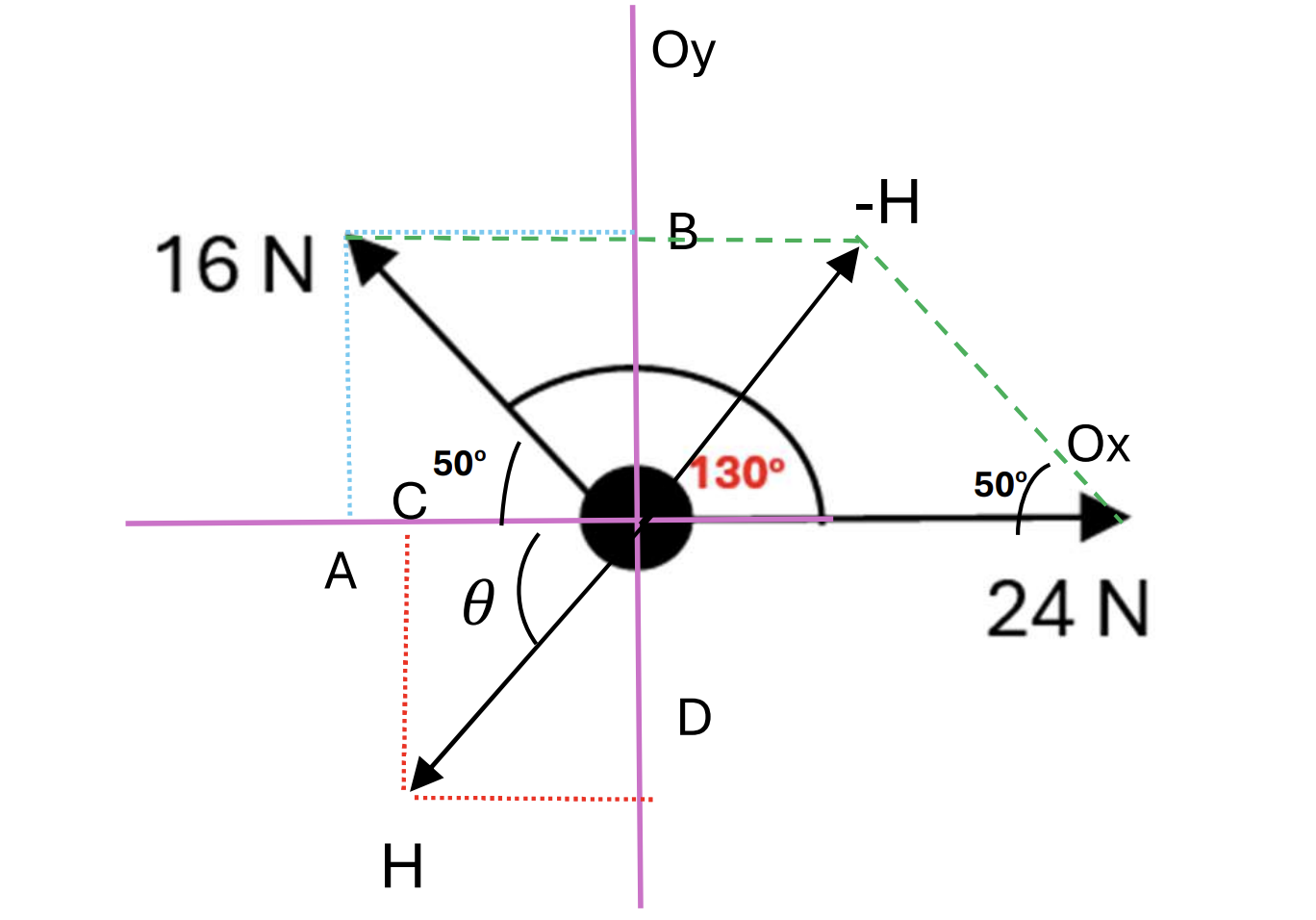
Solving 1:
At Ox, find that:
`vec(OA) + vec(OC) + vecF = 0` (system is in equilibrium), choose direction is to the right so:
OA + OC = F
`to 16cos50 + H.costheta = 24 N`
`costheta = frac(24 - 16cos50)(H)` (1)
At Oy, find that:
`vec(OD) + vec(OB) = 0` (system is in equilibrium), choose direction goes up so:
OB = OD
`to 16cos40= Hsintheta`
`sintheta = frac(16cos40)(H)` (2)
`(costheta)^2 + (sintheta)^2 = 1`
`to (frac(24-16cos50)(H))^2 + (frac(16cos40)(H))^2 = 1`
So H = 18.4 N [1]
`theta =` 41.81o
So takes 41.81o - 180o = -138.19 o is the value of angles between H and positve x-axis.
Solving 2:
a. Using cosine rule to calculate the magnitude of H.
`H^2 = 16^2 + 24^2 - 2*16 * 24 * cos50`
So H = 18.4 N
b. Sine rule: `sinX/16 = sin50/16`
`to X = 41.8^o`
So the angle with positive x- axis: -138.2o
Question 12
A book of weight 6 N lies on a smooth plane inclined at to the horizontal, where `tan beta = 3/4`
The book is held in equilibrium by a horizontal force of magnitude G N.
a. Draw all the force act on the book. [1]
b. Calculate the value of G N. [2]
a.
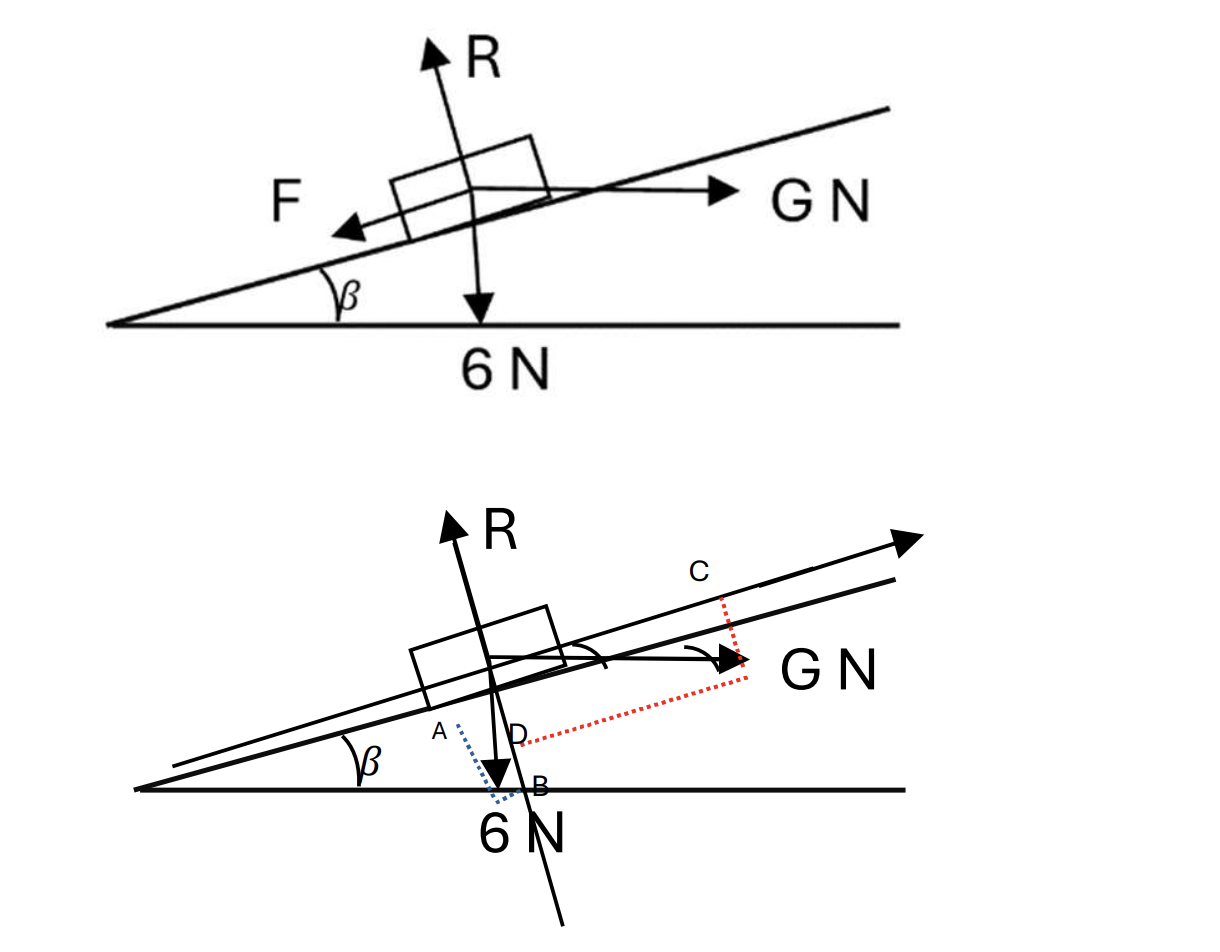
b. The friction force is negligible, so in Ox, find that:
`vec(OA) + vec(OC) = 0` (system is in equilibrium), choose direction is to the right so:
`OA = OC`
`to 6sinbeta = Gcosbeta`
`to tanbeta = G/6`
`to G = 4.5 N`
Question 13
Force J of magnitude 6N acts along Ox (the positive x -axis) and force K of magnitude 9N acts along Oy (the positive y-axis).
Force L of magnitude 10N acts at 50o Ox as shown in the diagram.
Find:
a. The magnitude of the resultant force [2]
The angle the resultant force makes with Ox [2]

a.
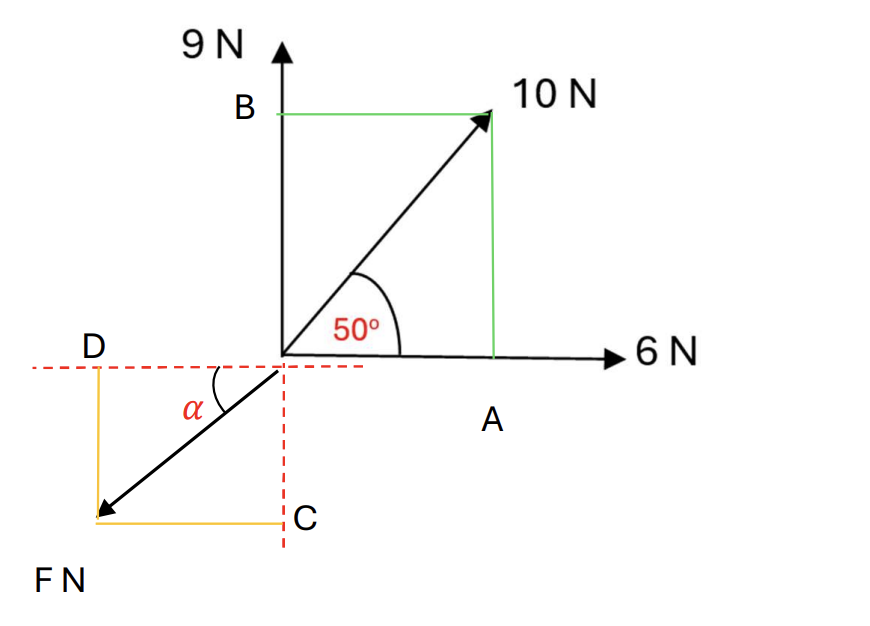
The resultant force is equal to the sum of the forces acting on an object, so `vecF = vecJ + vecK + vecL`
On Ox, we have:
`vecOA + vecJ + vecOD = 0`, choose the direction is to the right
`10cos50 + 6 = Fcosalpha` (1)
On Oy, we have:
`vecOC + vecK + vecOB = 0`, choose the direction goes up:
`10sin50 + 9 = Fsinalpha` (2)
Then, `frac(sinalpha)(cosalpha)` = `frac(10sin50 + 9)(10cos50 + 6)`
`to alpha = 53.3^o` [2]
`to F = 20.8 N` [2]
Question 14
A lawnmower of weight W N sits at rest on a grass slope inclined at an angle of `theta` to the slope. The grass slope is rough and the coefficient of friction betwwen the lawnmower and the grass is `mu`. The lawnmower is on the point of slipping down the grass slope.
a. Show that the tension in the cord is give by `frac(W(mucostheta - sintheta))(musintheta - costheta` [3]
b. Given that the tension is 15N, the weight is 80N and `theta` is 20o, find the value of `mu`. [1]

a.
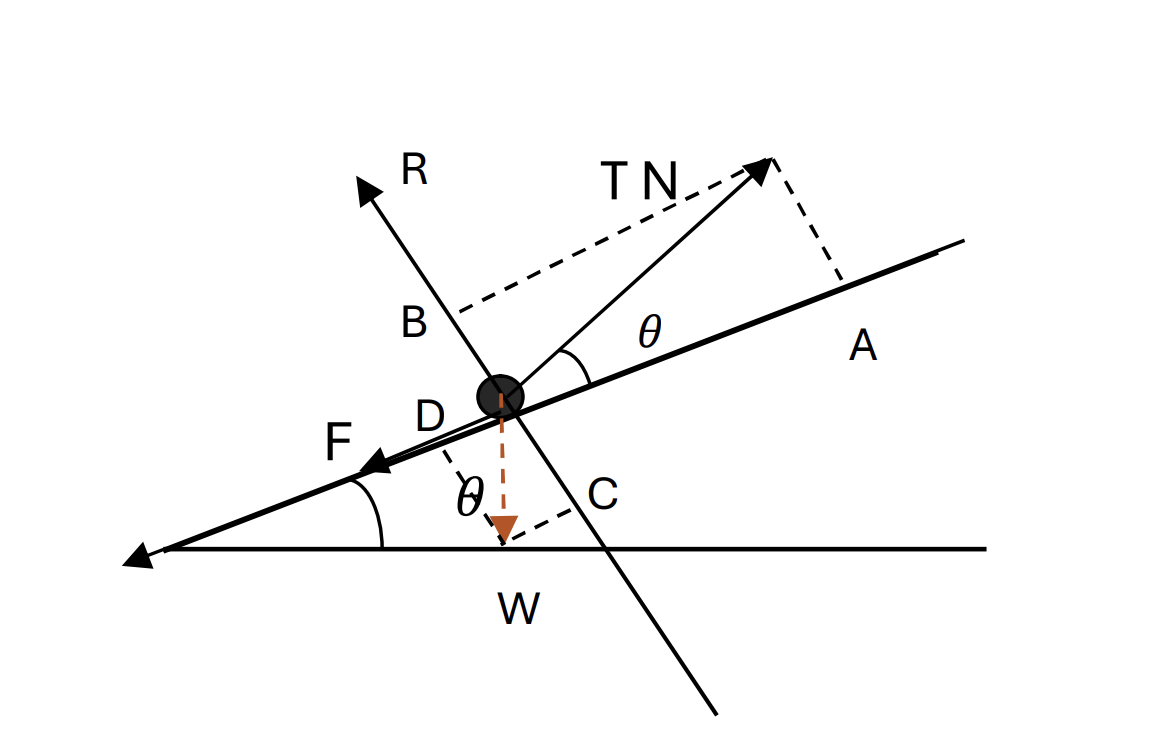
At Ox, find that:
`vec(OA) + vec(OD) + vecF = 0` (system is in equilibrium), choose direction is to the left so:
OA = OD + F
`to Tcostheta = Wsintheta + muR` (1) [1]
At Oy, find that:
`vec(OC) + vec(OB) + vec(R) = 0` (system is in equilibrium), choose direction goes up so:
OB + R = OC
`to R = Wcostheta - Tsintheta`(2) [1]
Subtitute R in equation (1) then we have `frac(W(mucostheta - sintheta))(musintheta - costheta)`
b. `mu = 0.189` [1]
Question 15
A rock of weight W N is about to slip down a rough slopr inclined at an angle of `theta` to the horizontal. The rock is held in position by a horizontal force of magnitude P N, where 5P = W. The coefficient of friction between the rock and the slope is `2/5`.
a. Draw all the force act on the rock. [1]
b. Show that tan`theta` = `37/33` [4]
a.
b.
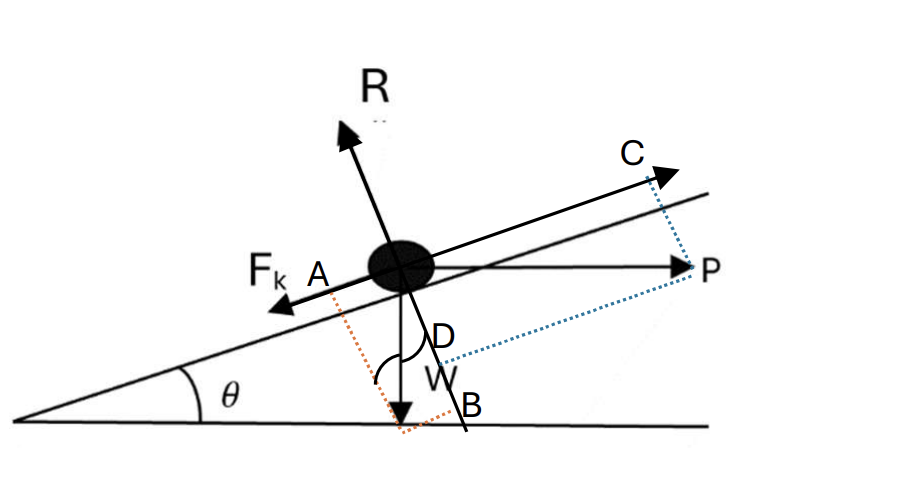
At Ox, find that:
`vec(OA) + vec(OC) + vec(F_k) = 0` (system is in equilibrium), choose direction is to the left so:
`OA = OC + F_k`
`to Wsintheta = Pcostheta + muR` (1)
`to R = frac(Wsintheta - Pcostheta)(mu`
At Oy, find that:
`vec(OD) + vec(OB) + vecR = 0` (system is in equilibrium), choose direction goes up so:
OB + OD = R
`to R = Wcostheta + P sintheta` (2) [2]
Subtitute R in equation (2)
Wcos ? + Psin`theta` = `frac(Wsintheta - P costheta)(mu)`
Dividing both sides for cos`theta`
W + `P tan theta = W/mu tantheta - P/mu` (we have `mu = 2/7; P = W/5)`
tan`theta = 17/23` [2]
Question 16
A table of weight W N is at rest on a rough plane. A force of P N, parallel to the line of greatest slope of the plane, is applied to the table such that the table is on the point of slipping up the slope. The value of P and the coefficient of friction `mu`,between the table and the plane remain constant when the plane is angled at each of `alpha` and `beta` to the horizontal where sin`alpha` = `3/5` and sin`beta = 8/17`
a. Show that P = `13W/7` [5]
b. Hence show that `mu` = `a/b`, where a and b are coprime and a + b = 19 [1]
a. We separate it into two ways:
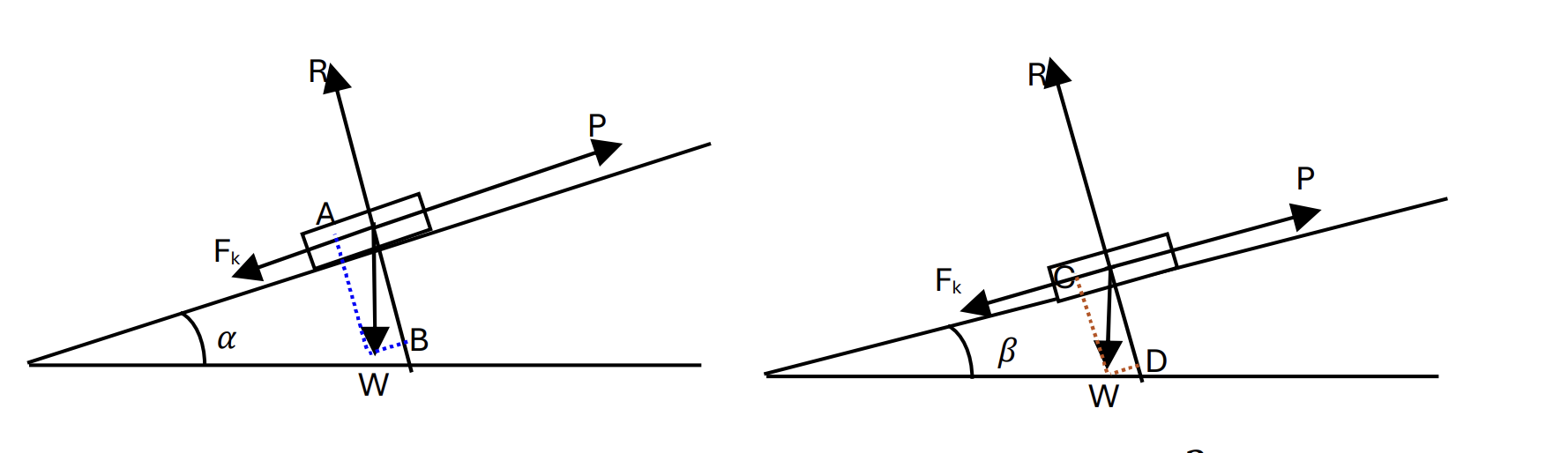
Firstly, we calculate on the diagram has sin`alpha` = `3/5`
At Ox, find that:
`vec(OA) + vec(F_k) + vecP = 0` (system is in equilibrium), choose direction is to the left so:
`A + F_k = P`
`to muR + Wsinbeta = P` (1)
At Oy, find that:
`vec(OB) + vecR = 0` (system is in equilibrium), choose direction goes up so:
OB = R
`to R = Wcosbeta` (2) [2]
Secondly, we calculate on the diagram has sin`beta = 8/17`
At Ox, find that:
`vec(OC) + vec(F_k) + vecP = 0`
(system is in equilibrium), choose direction is to the left so:
OC + Fk = P
`muR + Wsinalpha = P` (3)
At Oy, find that:
`vec(OD) + vec(R) = 0`
(system is in equilibrium), choose direction goes up so:
OD = R
R = Wcos? (4) [2]
Combining (1) to (4) and `mu`, O remains constan, we have:
`frac(P - Wsinbeta)(Wcosbeta) = frac(P - Wsinalpha)(Wcosalpha)` with `sinalpha = 3/5, cosalpha = 4/5, sinbeta = 8/17, cosbeta = 15/17`
So P = `13/7W`
b. We have `muR + Wsinalpha = P`
`mu = frac(13/7W - W3/5)(4/5W) = 11/7` [1]
Question 17

Given that tan`alpha = 12/5` and tan`theta = 4/3`, show that the coplanar forces shown in the diagram are in equilibrium.
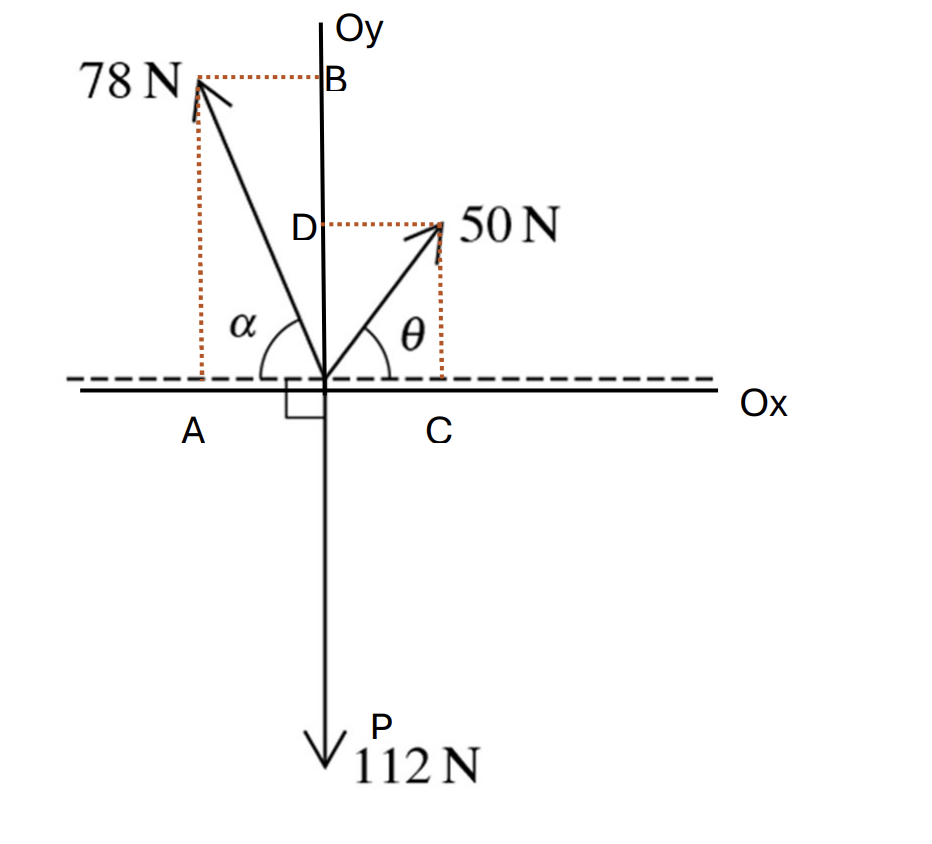
We have `alpha = 67.38^o; theta = 53.13^o`
At Ox, find that:
`vec(OA) + vec(OC) = 0` choose direction is to the left so:
OA = OC
`to 78cosalpha = 50costheta`
`to 78cos(67.38) = 50cos(53.13)`
`to 30 = 30` (Equilibrium at Ox)
At Oy, find that:
`vec(OD) + vec(OB) + vecP = 0` choose direction goes down so:
P = OD + OB
`P = 50 sintheta + 78 sinalpha`
`to P = 50sin(53.13) + 78sin(67.38)`
`to 112 = 112 (Equilibrium at Oy)`
So X = 0
Y = 0
The diagram shown is equilibrium.
Question 18

Coplanar forces of magnitudes 12N, 24N and 30N act at a point in the directions shown in the diagram.
a. Find the components of the resultant of the three forces in the x-direction and in the y-direction. [4]
b. Hence find the direction of the resultant. [2]
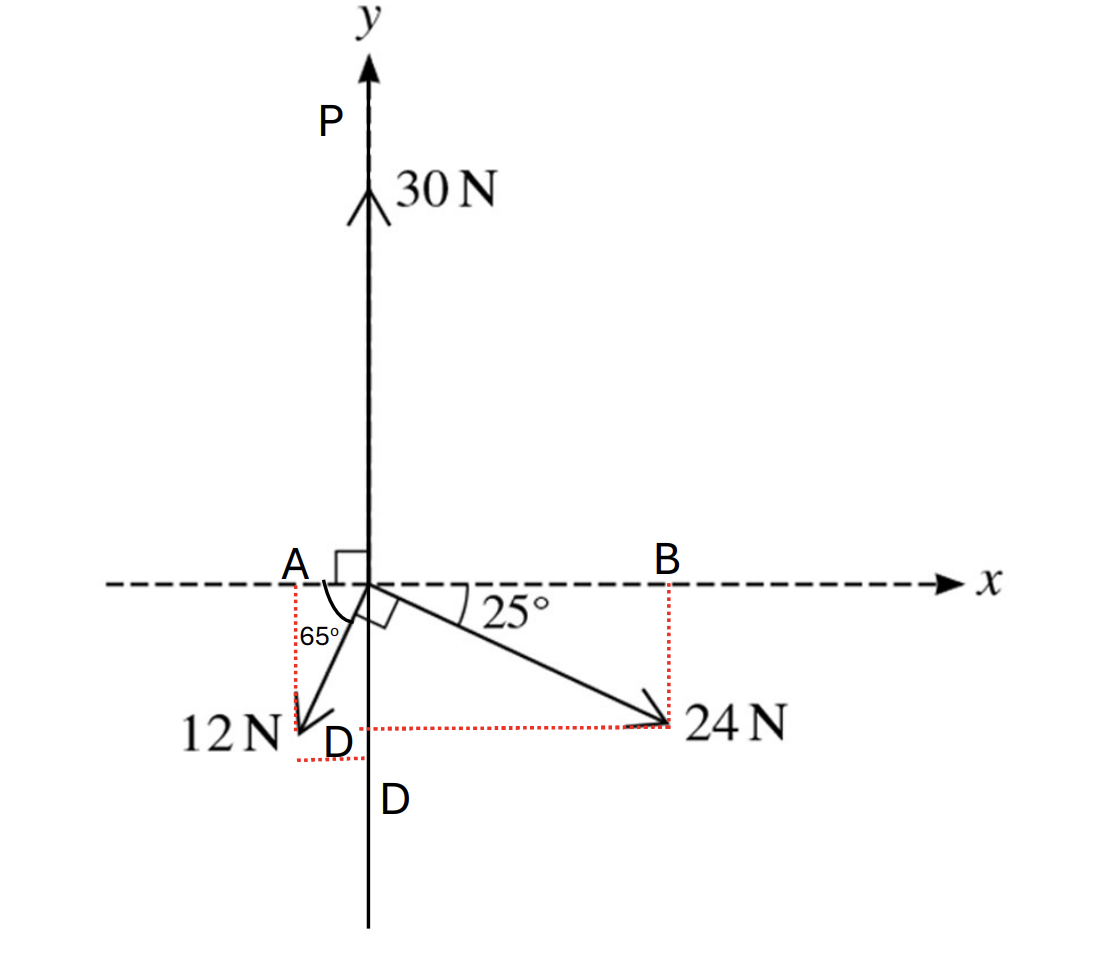
a. At Ox, find that:
`vec(OA) + vec(OB) = vec(Ox)` choose direction is to the right so:
OA − OB = Ox
`Ox = |12cos65 − 24cos25| = 16.7 N [2]`
At Oy, find that:
`vec(OC) + vec(OD) + vecP = vec(O_y)`, choose direction goes up so:
P − OC - OD= Oy
`to O_y = |30 − 12sin65 − 24sin25 | =`8.98N
b.
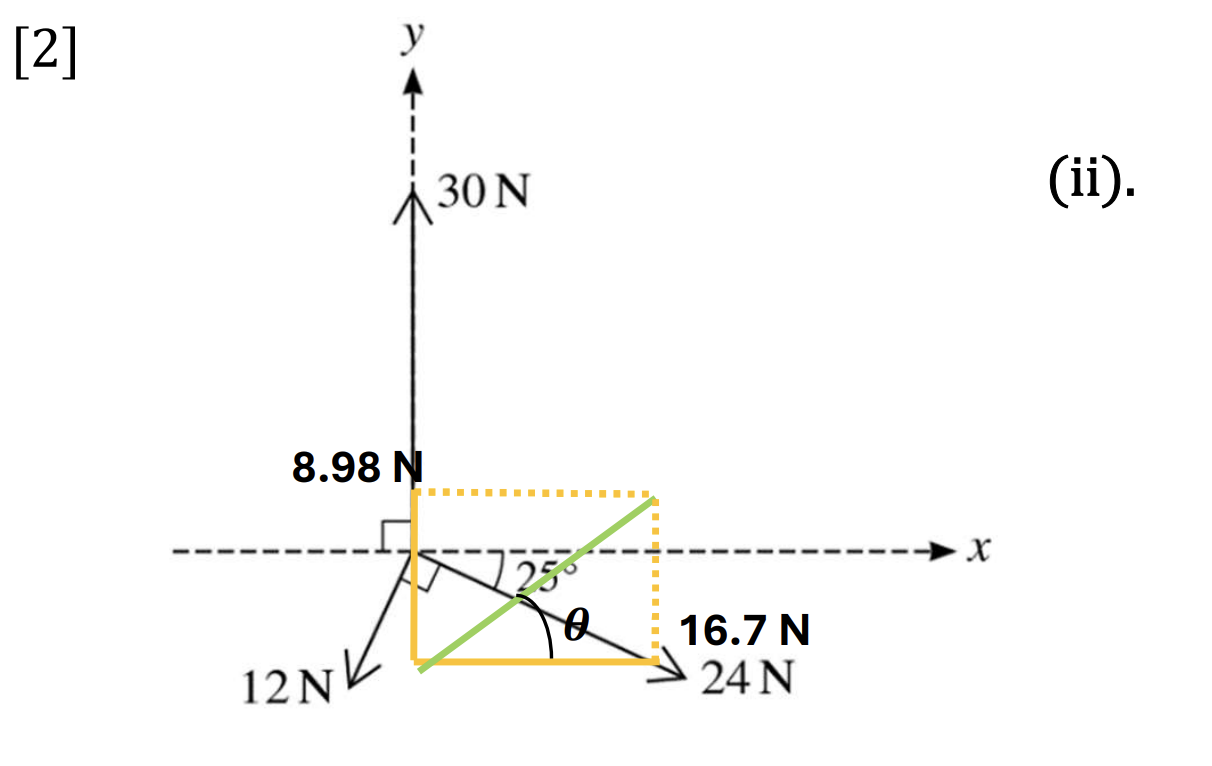
The angle `theta` calculates by using Right-angle triangle trigonometry:
tan`theta` = `8.98/16.7 = 0.54`
`theta = tan^-10.54 = 28.37^o`
The direction of the resultant has angle 28.37o which combines x-direction [2]
Question 19

A particle P of mass 0.3kg is held in equilibrium above a horizontal plane by a force of magnitude 5N, acting vertically upwards. The particle is attached to two strings PA and PB of lengths 0.9 m and 1.2 respectively. The points A and B lie on the plane and angle APB = 90o (see diagram).
Find the tension in each of the strings. [5]
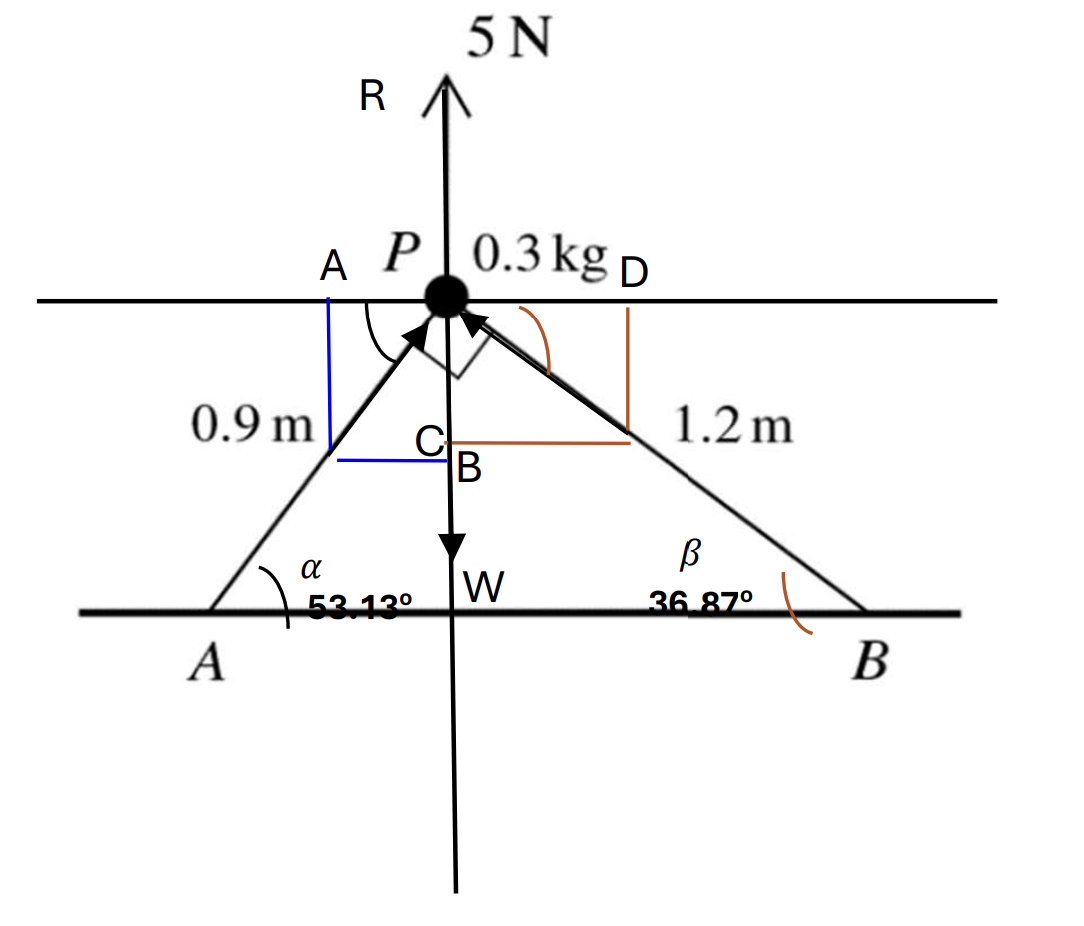
Using Right-angle triangle Trigonometric function, calculated the angle below: [1]
Angle `alpha = 53.13^o`
Angle `beta = 36.86^o`
Call a is the tension in string PA; b is the tension in string PB
At Ox, find that:
`vec(OA) + vec(OD) = 0` choose direction is to the left so:
OA = OD
`acos(53.13) - bcos(36.87) =`0
`to 0.6a - 0.8b = 0`(1) [1]
At Oy, find that:
`vec(OC) + vec(OB) + vecR + vecW = 0` choose direction goes up so:
OC + OB + W = R [1]
`to asin(53.13) + b sin(36.87) + 0.3*10 = 5`
`to 0.8a + 0.6b = 2` (2)
a = 1.6N [1]
b = 1.2 N [1]
Question 20

Coplanar forces of magnitude 8N, 12N and 18N act at a point in the direction shown in the diagram.
Find the magnitude and direction of the single additional force acting at the same point which will produce equilibrium. [6]
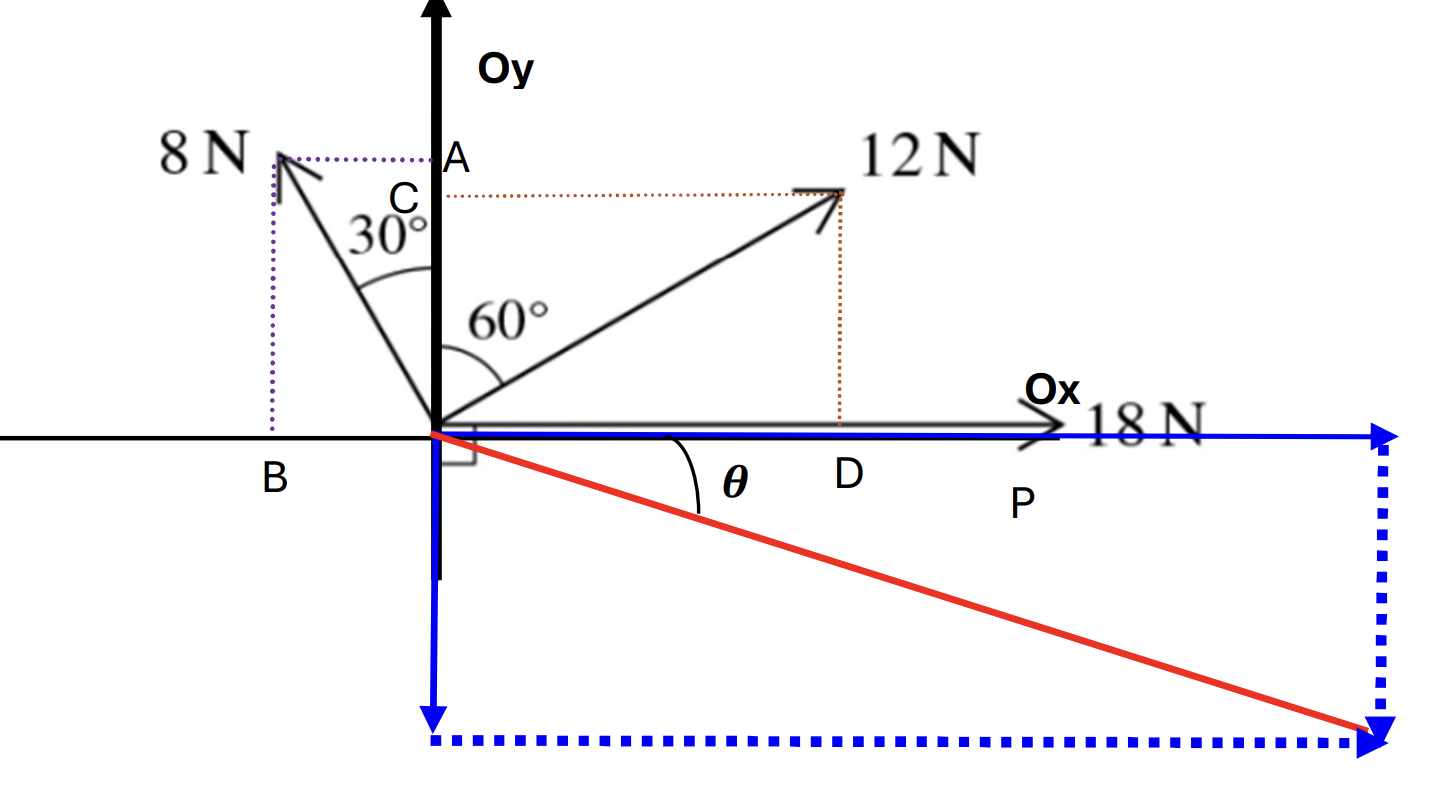
At Ox, find that:
`vec(OB) + vec(OD) + vecP = vec(Ox)` choose direction is to the right so:
OB - OD + 18 = Ox
`8sin(30) – 12sin(60) + 18 = Ox`
`to Ox = 6sqrt3 + 14` (1) [1]
At Oy, find that:
`vec(OC) + vec(OA) = 0` choose direction goes up so:
OC + OB = Oy [2]
`to Oy = 12cos(60) + 8cos(30) = 4sqrt3 + 6`[1]
So the resultant force is the red line, it calculates by Pythagoras theorem:
`F^2 = Ox^2 + Oy^2`
F = `sqrt((6sqrt3 + 14)^2 + (4sqrt3 + 6)^2) = 27.6N` [2]
`tantheta = frac(4sqrt3 + 6)(6sqrt3 + 14)`
`to theta = tan^-1(frac(4sqrt3 + 6)(6sqrt3 +14)) = 27.92^o` [1]
Direction is 27.9o below negative x- axis. [1]
Question 1

Three coplanar forces of magnitude 100N, 50N and 50 act at a point A, as shown in the diagram.
The value of cosα is `4/5`
Find the magnitude of the resultant of the three forces and state its direction. [3]
Question 2

Coplanar forces of magnitudes 20N, P N, 3 P N and 4 P N act at a point in the directions shown in the diagram.
The system is in equilibrium. Find P and `theta` [8]`
Question 3

A particle of mass 2.5 kg is held in equilibrium on a rough plane inclined at `20^o` to the horizontal by a force of magnitude T N making an angle of `60^o` with a line of greatest slope of the plane. The coefficient of friction between the particle and the plane is 0.3.
Find the greatest and least possible values of T. [8]
Question 4

Coplanar forces of magnitudes 8N, 12N, 10N and P N act at a point in the directions shown in the diagram. The system is in equilibrium.
Find P and `theta` [6]
Question 5

A block of mass m kg is held in equilibrium below a horizontal ceiling by two strings, as shown in the diagram. One of the strings is inclined at `45^o` to the horizontal and the tension is this string is T N. The other string is inclined at `60^o` to the horizontal and the tension in this string is 20N.
Find T and m. [5]
Question 6
A string is attached to a block of mass 4kg which rests in limiting equilibrium on a rough horizontal table. The string makes an angle of `24^o` above the horizontal and the tension in the string is 30N.
a. Draw a diagram showing all the forces acting on the block. [1]
b. Find the coefficient of friction between the block and the table. [5]
Question 7
A block of weight W N is pulled at a steady speed up a rough plane inclined at an angle of 2`27^o` by a cable of tension T N inclined at an angle of `15^o` to the plane. The reaction and friction force are given by R N and F N, respectively.
a. Draw a diagram showing all the forces acting on the block [1]
b. Given that `F = 1/2R`, so that `T/W`= `frac(cos27 + 2sin27)(2cos15 + sin15)` [6]
Question 8
A 20 N particle is held in limiting equilibrium by a horizontal force 14N on a rough slope which is inclined at an angle of `17^o` to the horizontal. The particle is on the point of slipping up the slope.
a. Draw a diagram showing all the forces acting on the particle [1]
b. Calculate the coefficient of friction [3]
Question 9
A force of magnitude P N is applied to a particle of weight 60N on a plane inclined at `theta` to the horizontal, where `sintheta = 11/61`. P acts parallel to the plane on a line of greatest slope up the plane. The coefficient of friction between the plane and the particle is 0.12; The particle is in limiting equilibrium.
a. Fill all the forces acting on the particles [1]
b. Find the range of values for P. [5]
Question 10
A particle is acted upon by three horizontal forces, P N, Q N and 25 N, as shown in the diagram. The Q N force acts due east and the 25N force acts due south. The P N forces acts on a bearing of`325^o`.
Given that the particle is in equilibrium, find:
a. The value of P. [1]
b. The value of Q. [1]

Question 11
Three forces, F, G and H, act upon a particle in a horizontal plane. Force F has a magnitude of 24 N and acts along the positive x-axis. Force G has a magnitude of 16 N and acts at an angle of `130^o` to the positive x-aixs as shown in the diagram. The three forces are in equilibrium.
a. Find the magnitude of H. [1]
b. Find the angle that H makes with the positive x – axis. [1]

Question 12
A book of weight 6 N lies on a smooth plane inclined at to the horizontal, where `tan beta = 3/4`
The book is held in equilibrium by a horizontal force of magnitude G N.
a. Draw all the force act on the book. [1]
b. Calculate the value of G N. [2]
Question 13
Force J of magnitude 6N acts along Ox (the positive x -axis) and force K of magnitude 9N acts along Oy (the positive y-axis).
Force L of magnitude 10N acts at 50o Ox as shown in the diagram.
Find:
a. The magnitude of the resultant force [2]
The angle the resultant force makes with Ox [2]

Question 14
A lawnmower of weight W N sits at rest on a grass slope inclined at an angle of `theta` to the slope. The grass slope is rough and the coefficient of friction betwwen the lawnmower and the grass is `mu`. The lawnmower is on the point of slipping down the grass slope.
a. Show that the tension in the cord is give by `frac(W(mucostheta - sintheta))(musintheta - costheta` [3]
b. Given that the tension is 15N, the weight is 80N and `theta` is 20o, find the value of `mu`. [1]

Question 15
A rock of weight W N is about to slip down a rough slopr inclined at an angle of `theta` to the horizontal. The rock is held in position by a horizontal force of magnitude P N, where 5P = W. The coefficient of friction between the rock and the slope is `2/5`.
a. Draw all the force act on the rock. [1]
b. Show that tan`theta` = `37/33` [4]
Question 16
A table of weight W N is at rest on a rough plane. A force of P N, parallel to the line of greatest slope of the plane, is applied to the table such that the table is on the point of slipping up the slope. The value of P and the coefficient of friction `mu`,between the table and the plane remain constant when the plane is angled at each of `alpha` and `beta` to the horizontal where sin`alpha` = `3/5` and sin`beta = 8/17`
a. Show that P = `13W/7` [5]
b. Hence show that `mu` = `a/b`, where a and b are coprime and a + b = 19 [1]
Question 17

Given that tan`alpha = 12/5` and tan`theta = 4/3`, show that the coplanar forces shown in the diagram are in equilibrium.
Question 18

Coplanar forces of magnitudes 12N, 24N and 30N act at a point in the directions shown in the diagram.
a. Find the components of the resultant of the three forces in the x-direction and in the y-direction. [4]
b. Hence find the direction of the resultant. [2]
Question 19

A particle P of mass 0.3kg is held in equilibrium above a horizontal plane by a force of magnitude 5N, acting vertically upwards. The particle is attached to two strings PA and PB of lengths 0.9 m and 1.2 respectively. The points A and B lie on the plane and angle APB = 90o (see diagram).
Find the tension in each of the strings. [5]
Question 20

Coplanar forces of magnitude 8N, 12N and 18N act at a point in the direction shown in the diagram.
Find the magnitude and direction of the single additional force acting at the same point which will produce equilibrium. [6]