Question 1
A particle travels 30 m in the negative direction, then 20 m in the positive direction. Find the overall distance traveled and the displacement from its original position. [2]
Easy
Mark as Complete
Mark Scheme
Question 2
A rocket is launched vertically upwards from the ground. It reaches a maxium height of 73 m, then returns to the ground.
a. Find the total distance travelled by the rocket [1]
b. Find the overall displacement of the rocket [1]
Easy
Mark as Complete
Mark Scheme
Question 3
A ball is launched upwards from the top of a 15 m tall building to a maximum height of 40 m, before falling to the ground. Taking upwards as the positive direction, find the overall distance travelled by the ball and the displacement of the ball from its original position. [2]
Easy
Mark as Complete
Mark Scheme
Question 4
A cyclist travels from her house to her grandparents’ house. She cycles 16 km east, then 16 km south. [3]
a. Find the bearing of her grandparents’ house from her own house.
b. Find her overall displacement.
c. How much further than her displacement did she cycle?
Easy
Mark as Complete
Mark Scheme
Question 5
A yatch sails at a constant speed for 20 minutes on a bearing of 120°, then for another 20 minutes on a bearing of 240°. After the journey, the yacht is 10km from its starting point. [2]
a. Find the distance sailed by the yatch.
b. Find the speed at which the yacht was sailing.
Medium
Mark as Complete
Mark Scheme
Question 6
A particle has an initial velocity of 60 ms-1 and constant deceleration of 8 ms-2. [2]
a. Find the velocity of the particle after 10 seconds.
b. Find the time at which the particle is at instantaneous rest.
Easy
Mark as Complete
Mark Scheme
Question 7
a. A particle at rest suddenly accelerates at 4 ms-2. How long does it take the particle to travel 128m? [1]
b. A particle travelling at 180 ms-1 starts to decelerate at a constant 3 ms-2. How many minutes does it take to return to its original position? [1]
c. A particle with an initial velocity of 5 ms-1 and a constant acceleration of 3 ms-2 takes T seconds to travel 84 m. Show that `3T^2 + 10T -168 = 0` and hence find the value of T. [1]
Easy
Mark as Complete
Mark Scheme
Question 8
J passes O at 2 ms-1 and a constant acceleration of 1 ms-2. When J is 30 m from O, K sets off from rest from O at a constant acceleration of 0.8 ms-2. When K reaches a velocity of 4 ms-1, L passes O at 3 ms-1 and a constant acceleration of 0.5 ms-2. If J, K and L are all travelling in the same direction along the same traight line, find the distance between J and K when L has a velocity of 7 ms-1. [7]
Hard
Mark as Complete
Mark Scheme
Question 9
A particle P is projected vertically upwards with speed 5 ms-1 from a point A which is 2.8 m above horizontal ground.
a.Find the greatest height above the ground reached by P. [3]
b.Find the length of time for which P is at a height of more than 3.6 m above the ground. [4]
Easy
Mark as Complete
Mark Scheme
Question 10
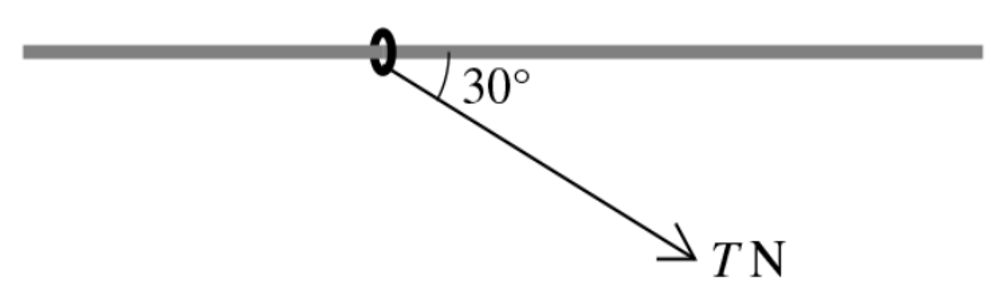
The diagram shows a ring of mass 0.1 kg threaded on a fixed horizontal rod. The rod is rough and the coefficient of friction between the ring and the rod is 0.8. A force of magnitude T N acts on the ring in a direction at 30° to the rod, downwards in the vertical plane containing the rod. Initially, the ring is at rest.
a.Find the greatest value of T for which the ring remains at rest.
b.Find the acceleration of the ring when `T=3`.
Medium
Mark as Complete
Mark Scheme
Question 11
A particle moves in a straight-line AB. The velocity v ms-1 of the particle t s after leaving A is given by `v = k(t^2-10t + 21)`, where k is a constant. The displacement of the particle from A, in the direction towards B, is 2.85 m when `t = 3` and is 2.4 m when `t = 6`.
a.Find the value of k. Hence find the expression, in term of t, for the displacement of the particle from A. [7]
b.Find the displacement of the particle from A when its velocity is a minimum. [4]
Medium
Mark as Complete
Mark Scheme
Question 12
A tram starts from rest and moves with uniform acceleration for 20 s. The tram then travels at a constant speed, V ms-1, for 170 s before being brought to rest with a uniform deceleration of magnitude twice that of the acceleration. The total distance travelled by the tram is 2.775 km.
a. Sketch a velocity-time graph for the motion, starting the total time for which the tram is moving [2]
b. Find V [2]
c. Find the magnitude of the acceleration [2]
Easy
Mark as Complete
Mark Scheme
Question 13
A particle P moves in a straight line. The velocity v ms-1 at time t s is given by
`v = 2t+1` for `0<=t<=5`,
`v = 36-t^2` for `5<=t<=7`,
`v = 2t-27` for `7<=t<=13.5`.
a. Sketch the velocity-time graph for `0<=t<=13.5` [3]
b. Find the acceleration at the instant when `t=6` [2]
c. Find the total distance traveled by P in the interval `0<=t<=13.5` [5]
Hard
Mark as Complete
Mark Scheme
Question 14
A particle travels in a straight-line PQ. The velocity of the particle t s after leaving P is v ms-1, where `v=4.5+4t-0.5t^2`.
a. Find the velocity of the particle at the instant when its acceleration is zero. [3]
b. The particle comes to instantaneous rest at Q. [6]
Find the distance PQ.
Easy
Mark as Complete
Mark Scheme
Question 15
A particle P moves in s straight line. It starts from rest at a point O on the line and at time t s after leaving O it has acceleration a ms-2, where `a=6t-18`.
Find the distance P moves before it comes to instantaneous rest. [6]
Medium
Mark as Complete
Mark Scheme
Question 16
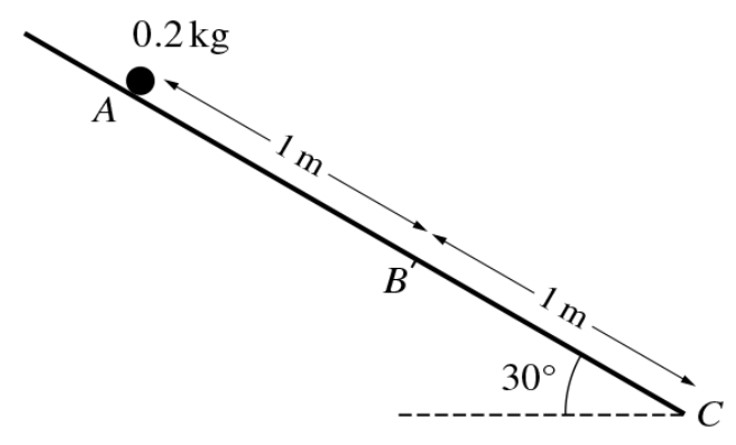
Three points A, B, and C lie on a line of greatest slope of a plane inclines at an angle of 30° to the horizontal, with AB = 1 m and BC = 1 m, as shown in the diagram. A particle of mass 0.2 kg is released from rest at A and slides down the plane. The part of the plane from A to B is smooth. The part of the plane from B to C is rough, with coefficient of friction μ between the plane and the particle.
a. Given that `μ=frac{1}{2}sqrt3`, find the speed of the particle at C. [8]
b. Given instead that the particle comes to rest at C, find the exact value of μ. [4]
Hard
Mark as Complete
Mark Scheme
Question 17
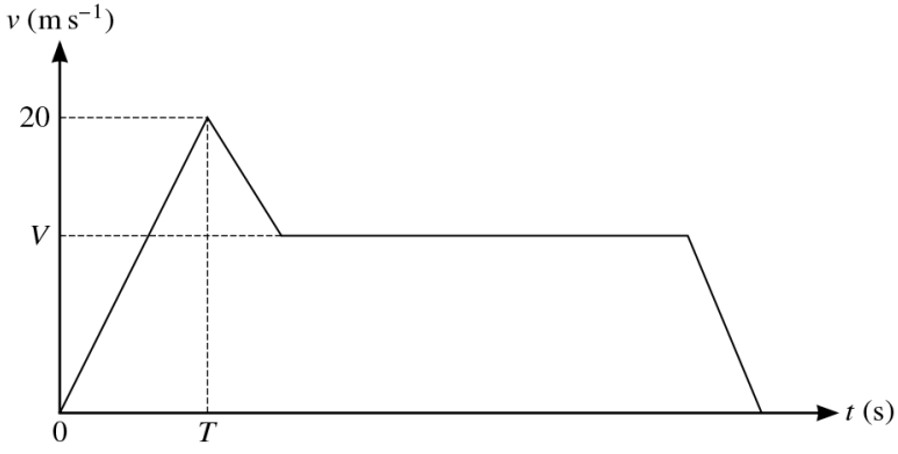
The diagram shows a velocity-time graph which models the motion of a car. The graph consists of four straight line segments. The car accelerates at a constant rate of 2 ms-2 from rest to a speed of 20 ms-1 over a period of T s. It then decelerates at a constant rate for 5 seconds before traveling at a constant speed of V ms-1 for 27.5 s. The car then decelerates to rest at a constant rate over a period of 5 s.
a. Find T [1]
b. Given that the distance traveled up to the point at which the car begins to move with constant speed is one-third of the total distance traveled, find V. [4]
Medium
Mark as Complete
Mark Scheme
Question 18
A particle P moves in a straight line, starting from a point O with velocity 1.72 ms-1. The acceleration a ms-1 of the particle, t s after leaving O, is given by `a=0.1xxt^{frac{3}{2}}`.
a. Find the value of t when the velocity of P is 3 ms-1. [4]
b. Find the displacement of P from O when `t=2`, giving your answer correct to 2 decimals places. [3]
Medium
Mark as Complete
Mark Scheme
Question 19
A particle P is projected vertically upwards with speed v ms-1 from a point on the ground. P reaches its greatest height after 3 s.
a. Find v [1]
b. Find the greatest height of P above the ground. [2]
Easy
Mark as Complete
Mark Scheme
Question 20
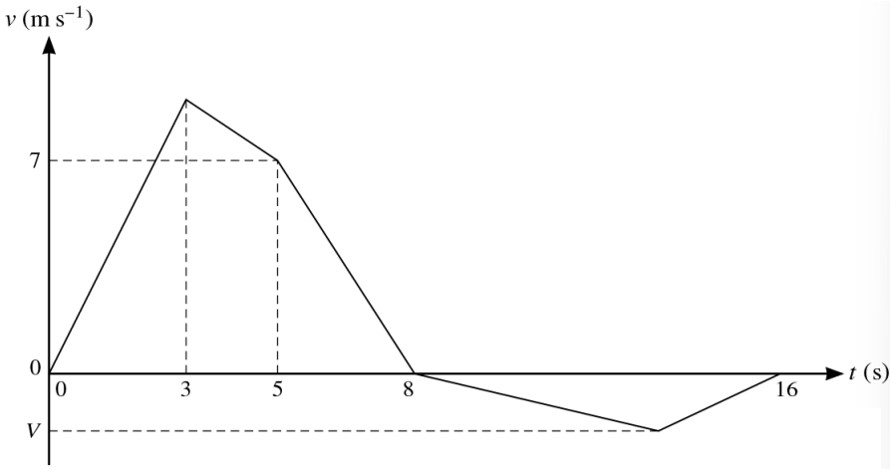
The velocity of a particle moving in a straight line is v ms-1 at time t seconds after leaving a fixed-point O. The diagram shows a velocity-time graph that models the motion of the particle from `t=0` to `t=16`. The graph consists of five straight-line segments. The acceleration of the particle from `t=0` to `t=3` is 3 ms-2. The velocity of the particle at `t=5` is 7 ms-1 and it comes to instantaneous rest at `t=8`. The particle then comes to rest again at `t=16`. The minimum velocity of the particle is V ms-1.
a. Find the distance traveled by the particle in the first 8 s of its motion. [3]
b. Given that when the particle comes to rest at `t=16` its displacement from 0 is 32 m, find the value of V. [4]
Easy
Mark as Complete
Mark Scheme
Question 1
A particle travels 30 m in the negative direction, then 20 m in the positive direction. Find the overall distance traveled and the displacement from its original position. [2]
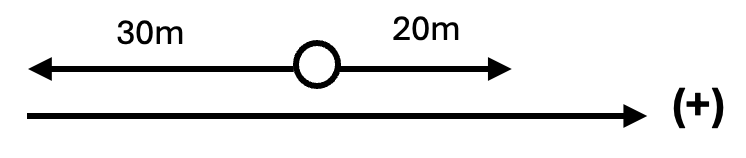
Choose positive direction is to the right
Displacement from original position `= -30 + 20 = -10` m [1]
The overall distance travelled `= 30 + 20 = 50` m [1]
Question 2
A rocket is launched vertically upwards from the ground. It reaches a maxium height of 73 m, then returns to the ground.
a. Find the total distance travelled by the rocket [1]
b. Find the overall displacement of the rocket [1]
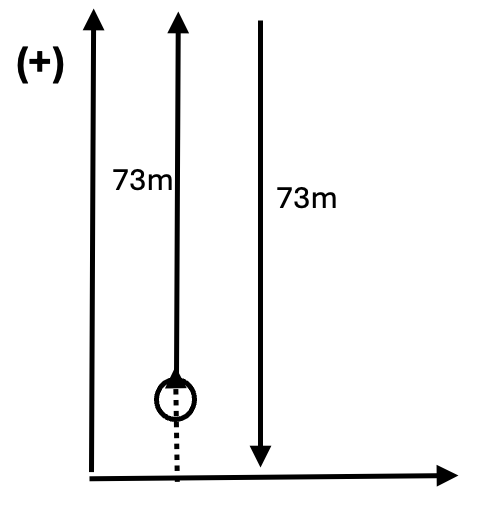
a. Total distance travelled by the rocket `= 73 + 73 = 146` m
b. Overall displacement of the rocket (Choose positive direction goes up) `= -73 + 73 = 0` m
Question 3
A ball is launched upwards from the top of a 15 m tall building to a maximum height of 40 m, before falling to the ground. Taking upwards as the positive direction, find the overall distance travelled by the ball and the displacement of the ball from its original position. [2]
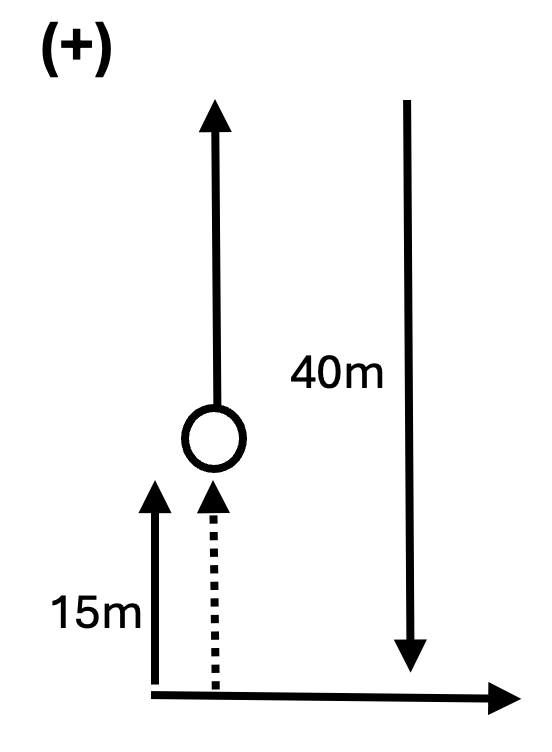
a. The overall distance travelled by the ball `=(40-15)+40=65` m
b. The displacement of the ball from its original position `= -40 + 25 = -15` m
Question 4
A cyclist travels from her house to her grandparents’ house. She cycles 16 km east, then 16 km south. [3]
a. Find the bearing of her grandparents’ house from her own house.
b. Find her overall displacement.
c. How much further than her displacement did she cycle?
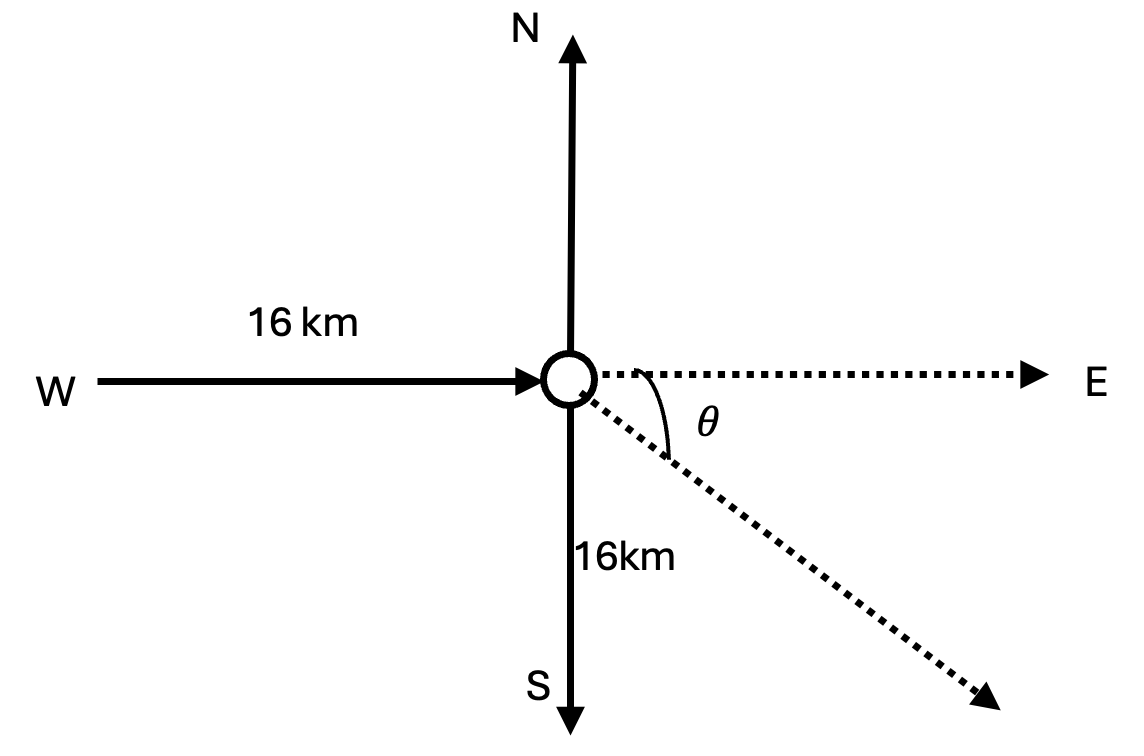
a. `tan^-1(frac{16}{16})=45°`
+ The bearing of her grandparents’ house from her own house is:
`90° + 45° = 135°` [1]
b. Overall displacement
`sqrt{16^2+16^2}=22.6` km [2]
c. She cycled further than her displacement
`32-22.6=9.4` km [3]
Question 5
A yatch sails at a constant speed for 20 minutes on a bearing of 120°, then for another 20 minutes on a bearing of 240°. After the journey, the yacht is 10km from its starting point. [2]
a. Find the distance sailed by the yatch.
b. Find the speed at which the yacht was sailing.

We have triangle ABC is equilateral because every angle has the same value is 60°, so AC = AB = 10 km.
a. The distance sailed by the yatch is AC + AB = 20 km [1]
b. The speed at which the yatch was sailing `=frac{20}{(frac{40}{60})}=30` km-1 [1]
Question 6
A particle has an initial velocity of 60 ms-1 and constant deceleration of 8 ms-2. [2]
a. Find the velocity of the particle after 10 seconds.
b. Find the time at which the particle is at instantaneous rest.
a. The velocity of the particle after 10 seconds:
`v=u+at`
`v=60-8.10=-20`ms-1 [1]
b. The time at which the particle is at instantaneous rest
`v=0`
`v=u+at`
`t=frac{v-u}{a}=frac{0-60}{-8}=7.5`s [1]
Question 7
a. A particle at rest suddenly accelerates at 4 ms-2. How long does it take the particle to travel 128m? [1]
b. A particle travelling at 180 ms-1 starts to decelerate at a constant 3 ms-2. How many minutes does it take to return to its original position? [1]
c. A particle with an initial velocity of 5 ms-1 and a constant acceleration of 3 ms-2 takes T seconds to travel 84 m. Show that `3T^2 + 10T -168 = 0` and hence find the value of T. [1]
a. `u=0`ms-1, `s=128`m, `a=4`ms-2
We have `s=ut+frac{1}{2}at^2`
`128=0t+frac{1}{2}4t^2`
So s [1]
b.`v=0`ms-1, `s=0`m, `a=-3`ms-2
We have
`0=180t+frac{1}{2}(-3)t^2`
So `t=0`s or s [1]
It takes 2 minutes to return to its original position.
c. `u=5`ms-1, `a=3`m, `s=84`ms-2
We have `s=ut+frac{1}{2}at^2`
`84=5T+frac{1}{2}3T^2`
`3T^2+10T-168=0`
`T=6`s and `T=-9.33`s
So `T=6`s [1]
Question 8
J passes O at 2 ms-1 and a constant acceleration of 1 ms-2. When J is 30 m from O, K sets off from rest from O at a constant acceleration of 0.8 ms-2. When K reaches a velocity of 4 ms-1, L passes O at 3 ms-1 and a constant acceleration of 0.5 ms-2. If J, K and L are all travelling in the same direction along the same traight line, find the distance between J and K when L has a velocity of 7 ms-1. [7]
At J: u = 2 ms-1, a = 1 ms-2, s = 30 m
`s=ut+frac{1}{2}at^2`
`30=2t+frac{1}{2}1t^2`
`t^2+4t-60=0`
`(t+10)(t-6)=0`
`t=6` s [1]
At K: u = 0 ms-1, a = 0.8 ms-2, v = 4 ms-1
`v=u+at`
`4=0+0.8t`
`t=5` s [1]
At L: u = 3 ms-1, a = 0.5 ms-2, v = 7 ms-1
`v=u+at`
`7=3+0.5t`
`t=8` s [1]
When L has a velocity of 7 ms-1, J has been moving for `6+5=19` s and K has been moving for `5+8=13` s. [1]
At J: u = 2 ms-1, a = 1 ms-2, t = 19 s
`s=ut+frac{1}{2}at^2`
`s=2xx19+frac{1}{2}xx1xx19^2`
`s=218.5` m [1]
Question 9
A particle P is projected vertically upwards with speed 5 ms-1 from a point A which is 2.8 m above horizontal ground.
a.Find the greatest height above the ground reached by P. [3]
b.Find the length of time for which P is at a height of more than 3.6 m above the ground. [4]
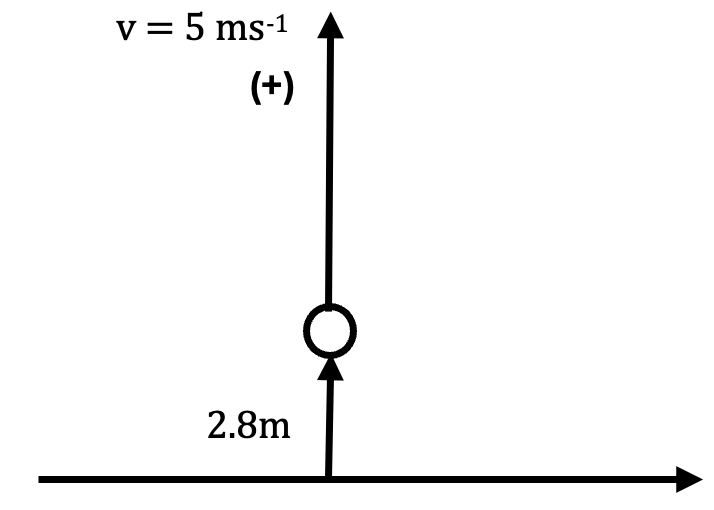
a. u = 0 ms-1; v = 5 ms-1; a = g = + 10 ms-2
`2gs=v^2-u^2` [1]
`s=frac{v^2-u^2}{2g}=frac{5^2-0^2}{2xx10}=1.25` m [1]
The greatest height above the ground reached by `P=1.25+2.8=4.05` m [1]
b. Find `s=3.6-2.8=0.8` m
`s=ut+frac{1}{2}at^2`
`t=0.2` or `t=0.8`
Length of time `=0.8-0.2=0.6` s
Question 10

The diagram shows a ring of mass 0.1 kg threaded on a fixed horizontal rod. The rod is rough and the coefficient of friction between the ring and the rod is 0.8. A force of magnitude T N acts on the ring in a direction at 30° to the rod, downwards in the vertical plane containing the rod. Initially, the ring is at rest.
a.Find the greatest value of T for which the ring remains at rest.
b.Find the acceleration of the ring when `T=3`.
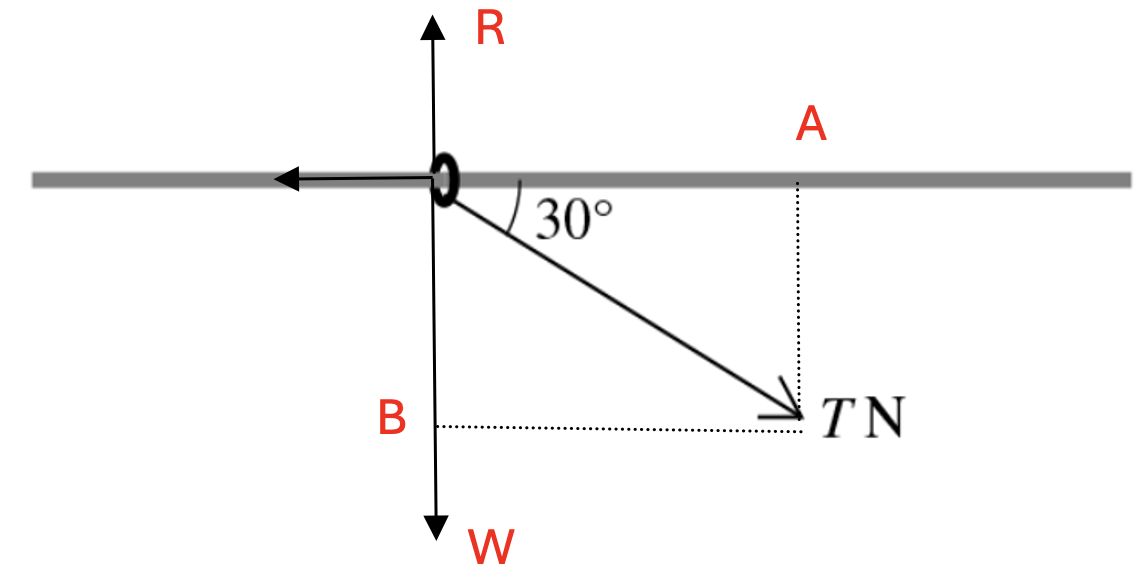
a. m = 0.1 kg; µ = 0.8
At Ox, the total force is calculated by:
`vec{F_k}+vec{OA}=vec{Ox}`
Choose the direction is to the left and the system is equilibrium
`F_k-OA=0`
`µR = OA = Tcos30` (1) [1]
At Oy, the total force is calculated by
`vecA+vecW+vec{OB}=vec{Oy}`
Choose the direction goes down and the system is equilibrium
`-R+OB+W=0`
`OB+W=R`
`Tsin30+0.1xx10=R` (2) [1]
Substitute R of (2) into (1), we have
`µ(Tsin30+0.1xx10)=Tcos30` [1]
So `T=1.72` N [1]
b. Using the total force in question a, we have
`R=3sin30+0.1g` [1]
`3cos30-0.8(3sin30+0.1g)=0.1a`
So `a=5.98` ms-2 [1]
Question 11
A particle moves in a straight-line AB. The velocity v ms-1 of the particle t s after leaving A is given by `v = k(t^2-10t + 21)`, where k is a constant. The displacement of the particle from A, in the direction towards B, is 2.85 m when `t = 3` and is 2.4 m when `t = 6`.
a.Find the value of k. Hence find the expression, in term of t, for the displacement of the particle from A. [7]
b.Find the displacement of the particle from A when its velocity is a minimum. [4]
a. If you integrate an expression for the velocity you will get an expression for the displacement.
`intk(t^2-10t+21)dt` [1]
`s=k(frac{1}{3}t^3-5t^2+21t)+C` [1]
`2.85=k(frac{1}{3}xx3^3-5xx3^2+21xx3)+C`
`27k+C=2.85` (1) [1]
`2.4=k(frac{1}{3}xx6^3-5xx6^2+21xx6)+C`
`18k+C=2.4` (2) [1]
From (1) and (2), we calculate `k=0.05` and `C=1.5` [1]
The displacement of the particle from A
`s=0.05(frac{1}{3}t^3-5t^2+21t)+1.5` [2]
The displacement of the particle from A when its velocity is at a minimum and its acceleration is also at a minimum. We use differential functions to calculate acceleration. [1]
So `a=[0.05(t^2-10t+21)]` [1]
`a=0.05(2t-10)=0`
`t=5` s
Min value of v is at `t=5` [1]
Displacement at `t=5` is
`s=0.05(frac{1}{3}xx5^3-5xx5^2+21xx5)+1.5=2.58` m [1]
Question 12
A tram starts from rest and moves with uniform acceleration for 20 s. The tram then travels at a constant speed, V ms-1, for 170 s before being brought to rest with a uniform deceleration of magnitude twice that of the acceleration. The total distance travelled by the tram is 2.775 km.
a. Sketch a velocity-time graph for the motion, starting the total time for which the tram is moving [2]
b. Find V [2]
c. Find the magnitude of the acceleration [2]
a.
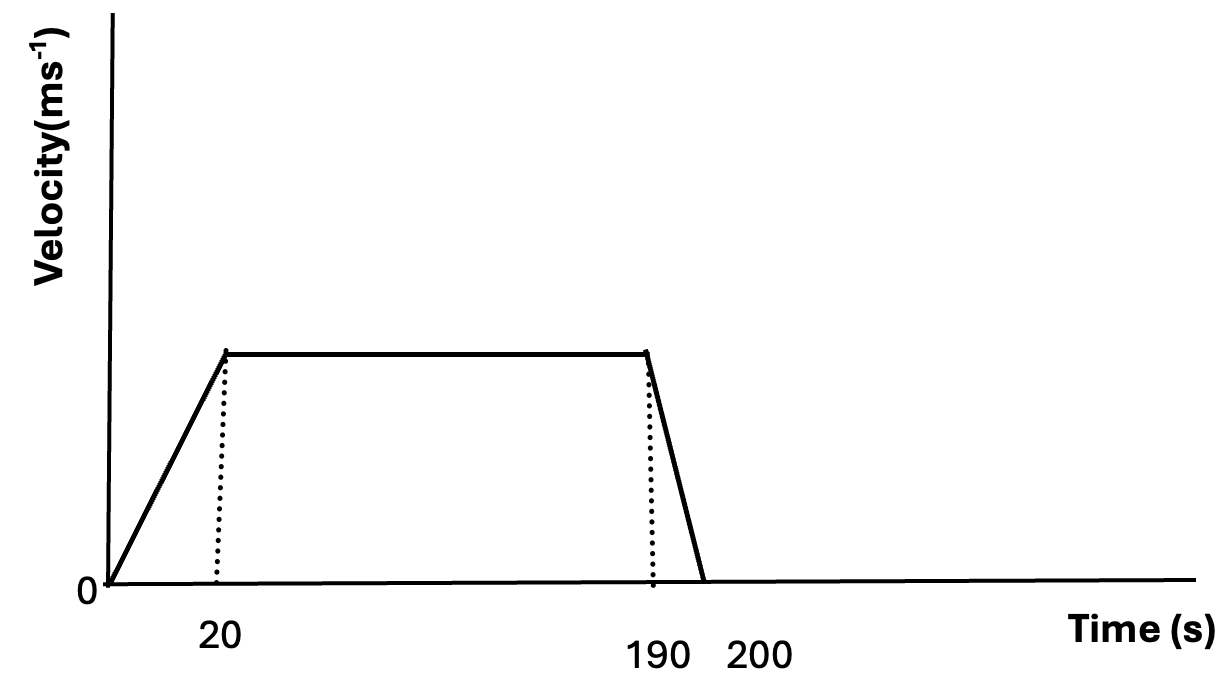 [2]
[2]
The time that the tram moved was from 0 to 200 s.
b. Total distance traveled by the tram was the area of trapezium.
Atrapezium `=frac{1}{2}(l_1+l_2)h=2775` [1]
So `frac{1}{2}(170+200)V=2775`
`V=frac{2xx2775}{170+200}=15` ms-1 [1]
c. The magnitude of the acceleration
`a=frac{v_f-v_i}{t_f-t_i}=frac{15-0){20}=0.75` ms-2 [2]
Question 13
A particle P moves in a straight line. The velocity v ms-1 at time t s is given by
`v = 2t+1` for `0<=t<=5`,
`v = 36-t^2` for `5<=t<=7`,
`v = 2t-27` for `7<=t<=13.5`.
a. Sketch the velocity-time graph for `0<=t<=13.5` [3]
b. Find the acceleration at the instant when `t=6` [2]
c. Find the total distance traveled by P in the interval `0<=t<=13.5` [5]
a. We have `v=2t+1` and `v=2t-27` is the linear equation and `v=36-t^2` is the parabolic equation. [1]
Step 1: With `v=2t+1`, we have the data table below:
| t (s) | 0 | 5 |
| v (ms-1) | 1 | 11 |
Step 2: With `v=36-t^2`, we have the data table below:
| t (s) | 5 | 6 | 7 |
| v (ms-1) | 11 | 0 | -13 |
Step 3: With `v=2t-27`, we have the data table below:
| t (s) | 7 | 10 | 13.5 |
| v (ms-1) | -13 | -7 | 0 |
Step 4: Sketch the graph
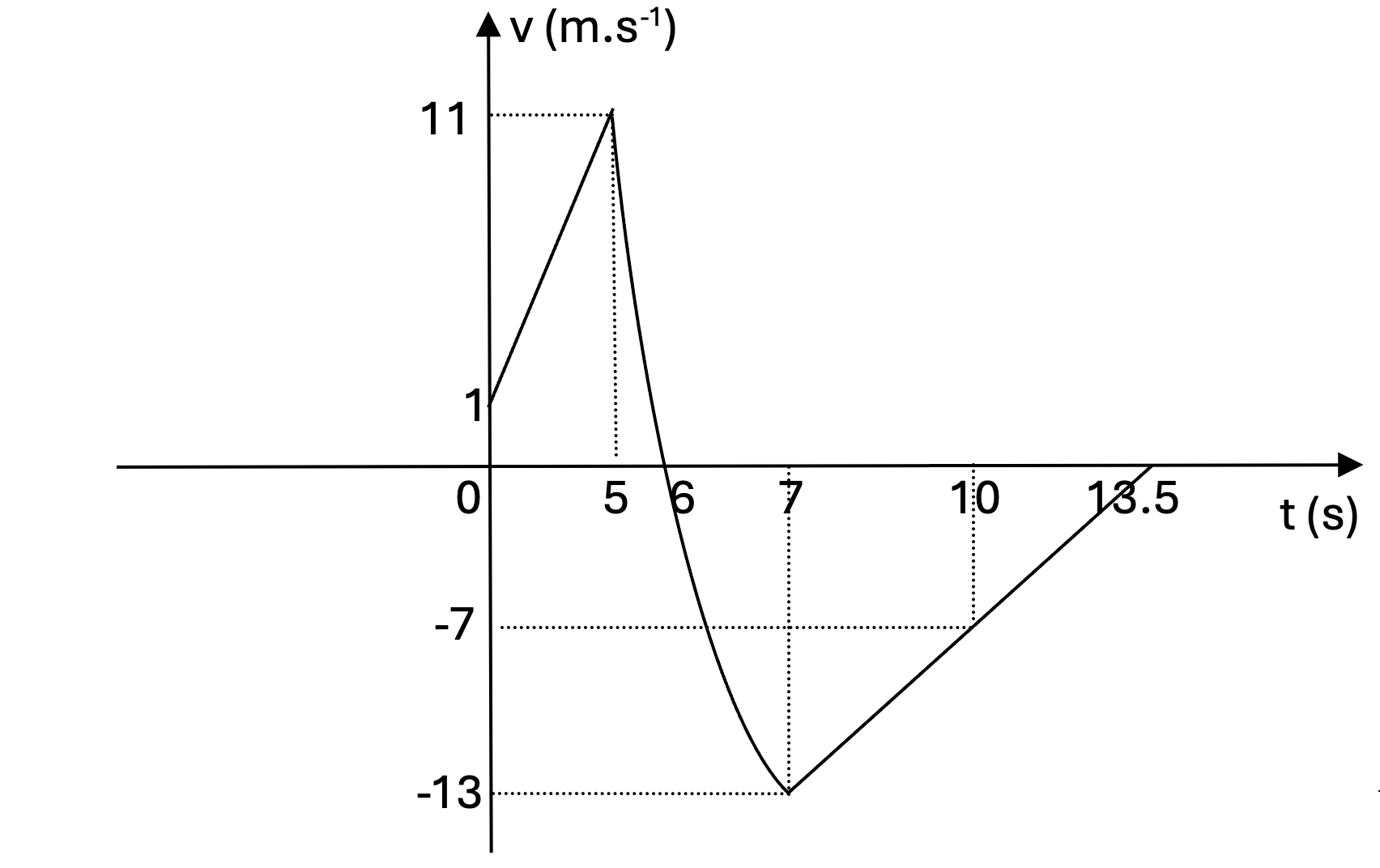 [2]
[2]
b. The acceleration at the instant when `t=6`
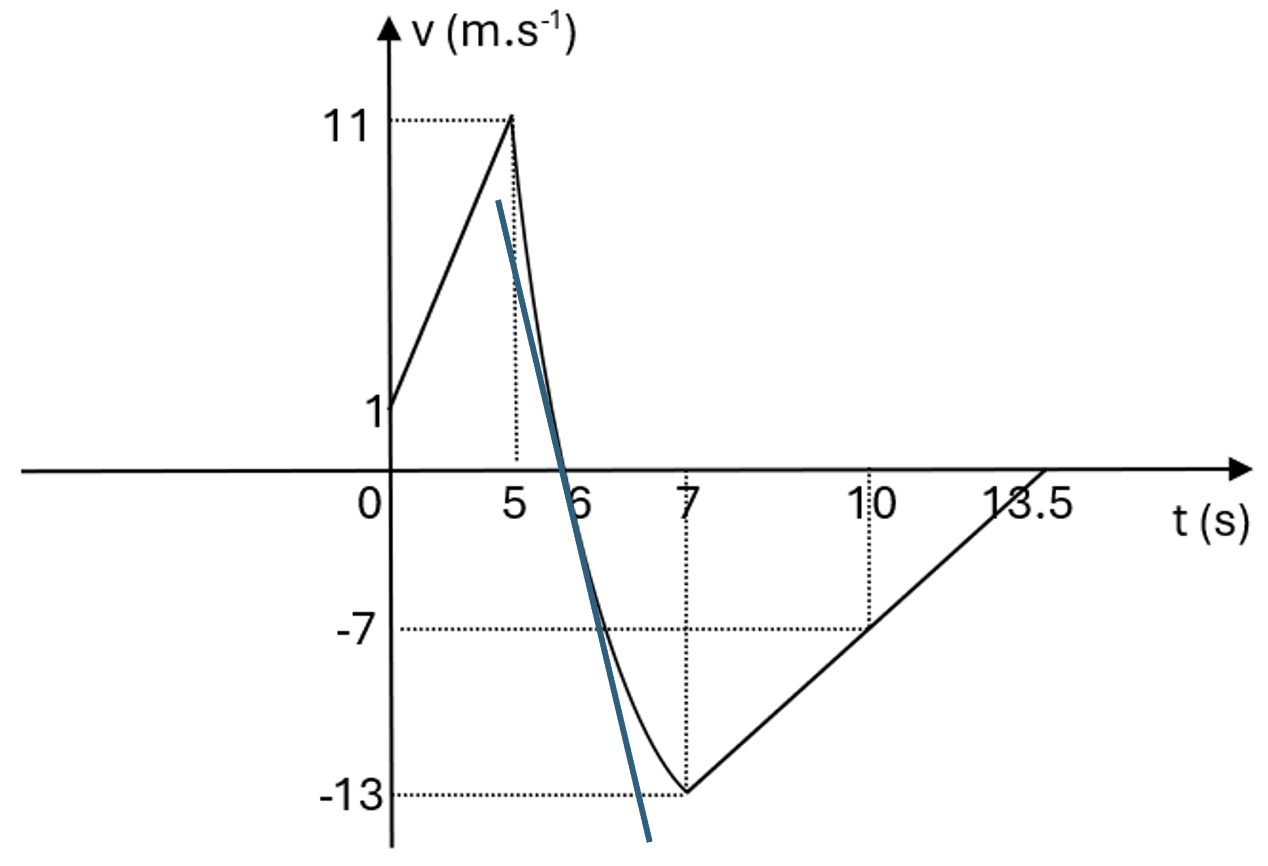
Find the gradient of the tangent at `t=6` by using the differential equation, we have:
`a=frac{dv}{dt}=-2t` [1]
`t=6` so `a=-2xx6=-12` ms-2 [1]
c. The total distance traveled by P in the interval `0<=t<=13.5` is calculated by using the integration equation. Therefore, the result is performed as below:
`s=int_0^5 f(2t+1)dt+int_5^6 f(36-t^2)dt+abs(int_5^6 f(36-t^2)dt+int_7^13.5 f(2t-27)dt)`
`s=(t^2+t)+(36t-frac{t^3}{3})+t^2-27t=84.24` m [5]
Question 14
A particle travels in a straight-line PQ. The velocity of the particle t s after leaving P is v ms-1, where `v=4.5+4t-0.5t^2`.
a. Find the velocity of the particle at the instant when its acceleration is zero. [3]
b. The particle comes to instantaneous rest at Q. [6]
Find the distance PQ.
a. To calculate the value of acceleration, we differentiate velocity to find it.
`a=frac{dv}{dt}=4-1t`
When acceleration is zero: `a=0`
`4-t=0`
`t=4`
So the velocity of the particle:
`v=4.5+4xx4-0.5xx4^2=12.5` ms-1
b. The particle comes to rest, `v=0` ms-1, so `4.5+4t-0.5t^2=0`
We have `t=9` and `t=-1` (reject)
We integrate velocity to find the distance to Q.
We have the limit of t is from 0 to 9, so the result will be:
`int_0^9 (4.5+4t-0.5t^2)dt`
So the distance is 81 m.
Question 15
A particle P moves in s straight line. It starts from rest at a point O on the line and at time t s after leaving O it has acceleration a ms-2, where `a=6t-18`.
Find the distance P moves before it comes to instantaneous rest. [6]
We integrate the acceleration to find velocity.
`int 6t-18dt` [1]
`=3t^2-18t+C` (1) [1]
Because P moves before it comes to instantaneous rest, so `v=0`
We have the equation: `3t^2-18t=0`
`t=0` or `t=6` (accepted) [1]
We continue to integrate the velocity to find displacement.
`int 3t^2-18t dt` [1]
`=t^3-9t^2+C` (2) [1]
Substitute `t=6` in the equation (1), so `s=108` m [1]
Question 16

Three points A, B, and C lie on a line of greatest slope of a plane inclines at an angle of 30° to the horizontal, with AB = 1 m and BC = 1 m, as shown in the diagram. A particle of mass 0.2 kg is released from rest at A and slides down the plane. The part of the plane from A to B is smooth. The part of the plane from B to C is rough, with coefficient of friction μ between the plane and the particle.
a. Given that `μ=frac{1}{2}sqrt3`, find the speed of the particle at C. [8]
b. Given instead that the particle comes to rest at C, find the exact value of μ. [4]
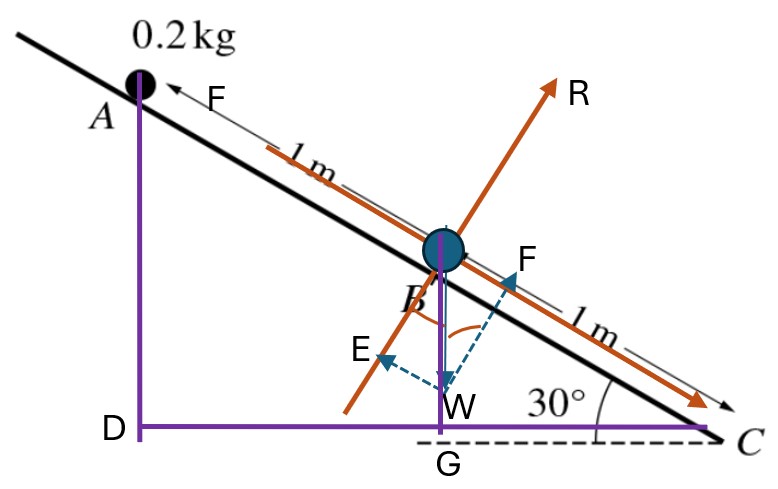
a. Firstly, we calculate AD to find the maximum height of the mass, use trigonometric ratio to find it.
`frac{AD}{AC}=sin30=>AD=2xxsin30=1` m [1]
At point A, the potential energy (PE) reaches the maximum value.
`PE=mgh=0.2xx10xx1=2` J [1]
At point B, applying the Mechanical Conservation Energy, the PE has transferred to kinetic energy (KE), in particular:
`KE=frac{1}{2}PE`
`frac{1}{2}xx0.2xxv_B^2=frac{1}{2}xx0.2xx10xx1`
`v_B=sqrt10=3.16` ms-1 [1]
At Oy, we have the total force:
`R=mgcos30=0.2xx10xxfrac{sqrt3}{2}=sqrt3` [1]
The Friction force `F_k=μR=frac{1}{2}sqrt3xxsqrt3=1.5` N [1]
At point B, the PE is calculated: `PE=mgh=0.2xx10xx0.5=1` J [1]
Work done against `F=1.5xx1=1.5` J [1]
Apply the Mechanical Conversation Energy, we have:
`frac{1}{2}xx0.2xx10+0.2xx10xx0.5=1.5xx1+frac{1}{2}xx0.2xxv_C^2`
`v_C=sqrt{10+2x-2.5xx1}=sqrt5` ms-1 `=2.24` ms-1 [1]
b. Using SUVAT equation, we have:
`v_C^2-v_B^2=2as`
`0-10=2xxaxx1` [1]
ms-2 [1]
Attempt Newton’s second law for motion from B to C
`0.2xx10xxsin30-F=0.2xx-5` [1]
`2=μsqrt3`
`μ=frac{2sqrt3}{3}` [1]
Question 17

The diagram shows a velocity-time graph which models the motion of a car. The graph consists of four straight line segments. The car accelerates at a constant rate of 2 ms-2 from rest to a speed of 20 ms-1 over a period of T s. It then decelerates at a constant rate for 5 seconds before traveling at a constant speed of V ms-1 for 27.5 s. The car then decelerates to rest at a constant rate over a period of 5 s.
a. Find T [1]
b. Given that the distance traveled up to the point at which the car begins to move with constant speed is one-third of the total distance traveled, find V. [4]
a. `a=frac{v_f-v_i}{T}`
`2=frac{20}{T}=>T=10` s [1]
b. Distance traveled before constant speed
`frac{1}{2}xx10xx20+frac{1}{2}xx(20+V)xx5`
`frac{1}{2}xx10xx20+frac{1}{2}xx(20+V)xx5+5V`
`[=150+2.5V]` [1]
Distance traveled after constant speed
`27.5V+frac{1}{2}xx5V[=30V]` [1]
`frac{1}{2}xx10xx20+frac{1}{2}xx(20+V)xx5=frac{1}{3}[frac{1}{2}xx10xx20+frac{1}{2}xx(20+V)xx5+27.5V+frac{1}{2}xx5V]` [1]
`V=12` [1]
Question 18
A particle P moves in a straight line, starting from a point O with velocity 1.72 ms-1. The acceleration a ms-1 of the particle, t s after leaving O, is given by `a=0.1xxt^{frac{3}{2}}`.
a. Find the value of t when the velocity of P is 3 ms-1. [4]
b. Find the displacement of P from O when `t=2`, giving your answer correct to 2 decimals places. [3]
a. To find the equation of velocity, we integrate the equation of acceleration.
`v=int0.1xxt^frac{3}{2}dt` [1]
`=0.04t^frac{5}{2}+C` (therein `C=1.72` ms-1)
`=0.04t^{frac{5}{2}}+1.72` [1]
To find t at P, we have:
`0.04t^{frac{5}{2}+1.72=3` [1]
`sqrt{t^5}=frac{3-1.72}{0.04}=32`
`t^5=32^2`
`t=root(5)(32^2)=4` [1]
b. To find the value of displacement, we integrate the equation of velocity.
`s=int(0.04t^{frac{5}{2}}+1.72)dt` [1]
`=frac{2}{175}t^{frac{7}{2}}+1.72t+C` (1)
We start from point P so `s=0` and `t=0` , solve (1), `C=0` [1]
So `s=frac{2}{175}t^{frac{7}{2}}+1.72t`
The displacement at `t=2` is `3.57` m [1]
Question 19
A particle P is projected vertically upwards with speed v ms-1 from a point on the ground. P reaches its greatest height after 3 s.
a. Find v [1]
b. Find the greatest height of P above the ground. [2]
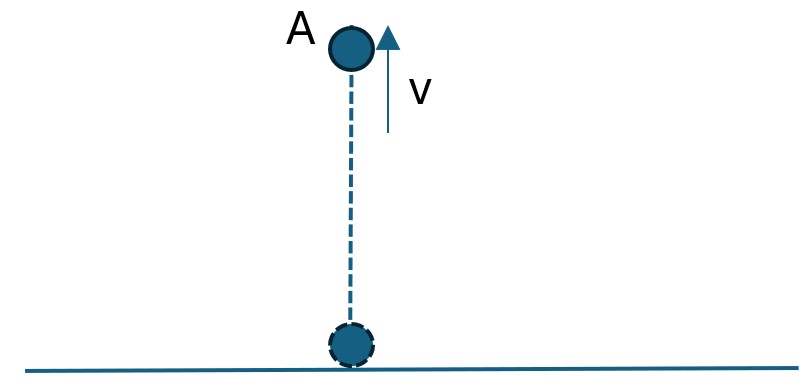
`v_y=v_{Oy}+axxt` (because the direction throws the particle is vertically upward, so `a=-g` and `v_{Oy}=0`)
`v_y=0-gxxt`
The magnitude of vy at `t=3` s is `v_y=|-10xx3|=30` ms-1
b. The greatest height of P above the ground (Applying the SUVAT equation)
`v^2-u^2=2as` (with `u=30` ms-1,`a=g=-10` ms-2,`v=0` ) [1]
`s=frac{-30^2}{2xx-10}=45` m [1]
Question 20

The velocity of a particle moving in a straight line is v ms-1 at time t seconds after leaving a fixed-point O. The diagram shows a velocity-time graph that models the motion of the particle from `t=0` to `t=16`. The graph consists of five straight-line segments. The acceleration of the particle from `t=0` to `t=3` is 3 ms-2. The velocity of the particle at `t=5` is 7 ms-1 and it comes to instantaneous rest at `t=8`. The particle then comes to rest again at `t=16`. The minimum velocity of the particle is V ms-1.
a. Find the distance traveled by the particle in the first 8 s of its motion. [3]
b. Given that when the particle comes to rest at `t=16` its displacement from 0 is 32 m, find the value of V. [4]
a. To find the distance by using diagram, we calculate the area under the graph.
`s=frac{1}{2}xx3xx9+frac{1}{2}xx(9+7)xx2+frac{1}{2}xx3xx7` [2]
`=40` m [1]
b. The displacement from 0 to 16 is 32 m, it is calculated by the area under the graph
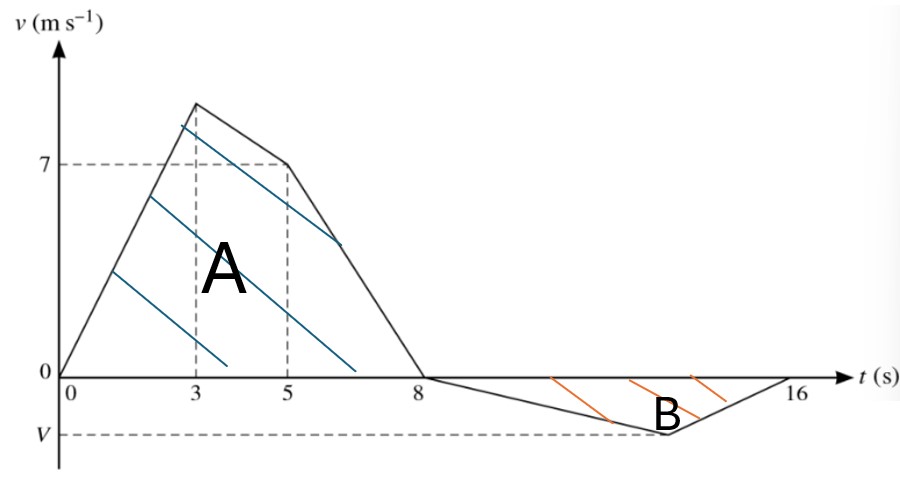
Area A + Area B = 32 m [1]
40 + Area B = 32
Area B = -8 m
`frac{1}{2}xxVxx8=-8` [1]
`V=-2` ms-1 [1]
Question 1
A particle travels 30 m in the negative direction, then 20 m in the positive direction. Find the overall distance traveled and the displacement from its original position. [2]
Question 2
A rocket is launched vertically upwards from the ground. It reaches a maxium height of 73 m, then returns to the ground.
a. Find the total distance travelled by the rocket [1]
b. Find the overall displacement of the rocket [1]
Question 3
A ball is launched upwards from the top of a 15 m tall building to a maximum height of 40 m, before falling to the ground. Taking upwards as the positive direction, find the overall distance travelled by the ball and the displacement of the ball from its original position. [2]
Question 4
A cyclist travels from her house to her grandparents’ house. She cycles 16 km east, then 16 km south. [3]
a. Find the bearing of her grandparents’ house from her own house.
b. Find her overall displacement.
c. How much further than her displacement did she cycle?
Question 5
A yatch sails at a constant speed for 20 minutes on a bearing of 120°, then for another 20 minutes on a bearing of 240°. After the journey, the yacht is 10km from its starting point. [2]
a. Find the distance sailed by the yatch.
b. Find the speed at which the yacht was sailing.
Question 6
A particle has an initial velocity of 60 ms-1 and constant deceleration of 8 ms-2. [2]
a. Find the velocity of the particle after 10 seconds.
b. Find the time at which the particle is at instantaneous rest.
Question 7
a. A particle at rest suddenly accelerates at 4 ms-2. How long does it take the particle to travel 128m? [1]
b. A particle travelling at 180 ms-1 starts to decelerate at a constant 3 ms-2. How many minutes does it take to return to its original position? [1]
c. A particle with an initial velocity of 5 ms-1 and a constant acceleration of 3 ms-2 takes T seconds to travel 84 m. Show that `3T^2 + 10T -168 = 0` and hence find the value of T. [1]
Question 8
J passes O at 2 ms-1 and a constant acceleration of 1 ms-2. When J is 30 m from O, K sets off from rest from O at a constant acceleration of 0.8 ms-2. When K reaches a velocity of 4 ms-1, L passes O at 3 ms-1 and a constant acceleration of 0.5 ms-2. If J, K and L are all travelling in the same direction along the same traight line, find the distance between J and K when L has a velocity of 7 ms-1. [7]
Question 9
A particle P is projected vertically upwards with speed 5 ms-1 from a point A which is 2.8 m above horizontal ground.
a.Find the greatest height above the ground reached by P. [3]
b.Find the length of time for which P is at a height of more than 3.6 m above the ground. [4]
Question 10

The diagram shows a ring of mass 0.1 kg threaded on a fixed horizontal rod. The rod is rough and the coefficient of friction between the ring and the rod is 0.8. A force of magnitude T N acts on the ring in a direction at 30° to the rod, downwards in the vertical plane containing the rod. Initially, the ring is at rest.
a.Find the greatest value of T for which the ring remains at rest.
b.Find the acceleration of the ring when `T=3`.
Question 11
A particle moves in a straight-line AB. The velocity v ms-1 of the particle t s after leaving A is given by `v = k(t^2-10t + 21)`, where k is a constant. The displacement of the particle from A, in the direction towards B, is 2.85 m when `t = 3` and is 2.4 m when `t = 6`.
a.Find the value of k. Hence find the expression, in term of t, for the displacement of the particle from A. [7]
b.Find the displacement of the particle from A when its velocity is a minimum. [4]
Question 12
A tram starts from rest and moves with uniform acceleration for 20 s. The tram then travels at a constant speed, V ms-1, for 170 s before being brought to rest with a uniform deceleration of magnitude twice that of the acceleration. The total distance travelled by the tram is 2.775 km.
a. Sketch a velocity-time graph for the motion, starting the total time for which the tram is moving [2]
b. Find V [2]
c. Find the magnitude of the acceleration [2]
Question 13
A particle P moves in a straight line. The velocity v ms-1 at time t s is given by
`v = 2t+1` for `0<=t<=5`,
`v = 36-t^2` for `5<=t<=7`,
`v = 2t-27` for `7<=t<=13.5`.
a. Sketch the velocity-time graph for `0<=t<=13.5` [3]
b. Find the acceleration at the instant when `t=6` [2]
c. Find the total distance traveled by P in the interval `0<=t<=13.5` [5]
Question 14
A particle travels in a straight-line PQ. The velocity of the particle t s after leaving P is v ms-1, where `v=4.5+4t-0.5t^2`.
a. Find the velocity of the particle at the instant when its acceleration is zero. [3]
b. The particle comes to instantaneous rest at Q. [6]
Find the distance PQ.
Question 15
A particle P moves in s straight line. It starts from rest at a point O on the line and at time t s after leaving O it has acceleration a ms-2, where `a=6t-18`.
Find the distance P moves before it comes to instantaneous rest. [6]
Question 16

Three points A, B, and C lie on a line of greatest slope of a plane inclines at an angle of 30° to the horizontal, with AB = 1 m and BC = 1 m, as shown in the diagram. A particle of mass 0.2 kg is released from rest at A and slides down the plane. The part of the plane from A to B is smooth. The part of the plane from B to C is rough, with coefficient of friction μ between the plane and the particle.
a. Given that `μ=frac{1}{2}sqrt3`, find the speed of the particle at C. [8]
b. Given instead that the particle comes to rest at C, find the exact value of μ. [4]
Question 17

The diagram shows a velocity-time graph which models the motion of a car. The graph consists of four straight line segments. The car accelerates at a constant rate of 2 ms-2 from rest to a speed of 20 ms-1 over a period of T s. It then decelerates at a constant rate for 5 seconds before traveling at a constant speed of V ms-1 for 27.5 s. The car then decelerates to rest at a constant rate over a period of 5 s.
a. Find T [1]
b. Given that the distance traveled up to the point at which the car begins to move with constant speed is one-third of the total distance traveled, find V. [4]
Question 18
A particle P moves in a straight line, starting from a point O with velocity 1.72 ms-1. The acceleration a ms-1 of the particle, t s after leaving O, is given by `a=0.1xxt^{frac{3}{2}}`.
a. Find the value of t when the velocity of P is 3 ms-1. [4]
b. Find the displacement of P from O when `t=2`, giving your answer correct to 2 decimals places. [3]
Question 19
A particle P is projected vertically upwards with speed v ms-1 from a point on the ground. P reaches its greatest height after 3 s.
a. Find v [1]
b. Find the greatest height of P above the ground. [2]
Question 20

The velocity of a particle moving in a straight line is v ms-1 at time t seconds after leaving a fixed-point O. The diagram shows a velocity-time graph that models the motion of the particle from `t=0` to `t=16`. The graph consists of five straight-line segments. The acceleration of the particle from `t=0` to `t=3` is 3 ms-2. The velocity of the particle at `t=5` is 7 ms-1 and it comes to instantaneous rest at `t=8`. The particle then comes to rest again at `t=16`. The minimum velocity of the particle is V ms-1.
a. Find the distance traveled by the particle in the first 8 s of its motion. [3]
b. Given that when the particle comes to rest at `t=16` its displacement from 0 is 32 m, find the value of V. [4]