Question 1
Calculate the momentum of:
a. A tennis ball of mass 0.056kg and velocity 35 ms-1. [1]
b. A piano of mass 160kg falling with a speed of 10 ms-1. [1]
c. A lion of mass 180kg running at a speed of 30kmh-1. [1]
Easy
Mark as Complete
Mark Scheme
Question 2
Annie and her younger brother Ryan are at the ice rink. They stand facing each other, then Annie pushes against Ryan and they both move backwards. Annie estimates that her movement is 1.5 ms-1.
Given that Annie has mass 40kg and Ryan has mass 30kg, how fast is Ryan moving? [2]
Easy
Mark as Complete
Mark Scheme
Question 3
Particle P of mass m kg and Q of mass 0.2 kg are free to move on a smooth horizontal plane.
P is projected at a speed of 2 ms-1 towards Q which is stationary. After the collision P and W move in opposite direction with speed of 0.5 ms-1 and 1 ms-1 respectively.
Find m [3]
Easy
Mark as Complete
Mark Scheme
Question 4
Two particles P and Q of masses 0.2kg and 0.5kg respectively, are at rest on smooth horizontal plane. P is projected towards Q with speed 2ms-1.
a. Write down the momentum of P [1]
b. After the collision P continues to move in the same direction with speed 0.3 ms-1.
Find the speed of Q after the collision [2]
Easy
Mark as Complete
Mark Scheme
Question 5
Ryan makes a cart, which he can jump onto and move, He decides to test it on a smooth, flat road. He stands on it, but it does not move.
We He tries again, jumping from a standing position and landing on the cart with a horizontal speed of 0.5 ms-1. Ryan has a mass of 40 kg and the cart has a mass of 12 kg.
a. Calculate the speed of the cart with Ryan riding on it. [2]
He tries a running start, starting 2m away from the cart and accelerating from rest at a rate of 0.25 ms-2.
b. Calculate the new speed of cart with Ryan riding on it. [3]
He wants the cart to go at a speed of 2ms-1.
c. How far will he have to run at this same rate of acceleration, before jumping into the cart, to achieve this final speed? Is this a realistic situation? [3]
Medium
Mark as Complete
Mark Scheme
Question 6
a. A basketball weighs 13 times more than a golf ball. If they are thrown at each other with an equal and opposite velocity u, show that vg = 12u – 13vb where vg is velocity of the golf ball after impact and vb is the velocity of the basketball after impact. [2]
b. A bullet of mass m kg is fired from a gun of mass M kg, which is free to recoil. Let the initial velocities of the bullet and gun be u ms-1 and U ms-1, respectively.
Show that the initial speeds of the bullet and gun are in inverse ratio to their masses. [3]
Medium
Mark as Complete
Mark Scheme
Question 7
A bus of mass 10 tonnes is following a car of mass 1.2 tonnes at a distance of 30m. Initially, both are travelling at a constant speed of 36 kmh-1 . The driver’s foot slips and causes the bus to accelerate uniformly. After 5 seconds, the bus crashes into the back of the car, and the two vehicles coalesce.
Find the acceleration (in ms-1) of the bus and the velocity (in kmh-1) of the vehicles immediately after the crash. [5]
Medium
Mark as Complete
Mark Scheme
Question 8
A particle B of mass 5 kg is at rest on a smooth horizontal table. A particle A of mass 2.5 kg moves on the table with a speed of 6 ms-1 and collides directly with B. In the collision the two particles coalesce.
a. Find the speed of the combined particle after the collision. [2]
b. Find the loss of kinetic energy of the system due to the collision. [3]
Medium
Mark as Complete
Mark Scheme
Question 9
Two objects A and B of mass 4.5kg and m kg approach each other at speeds of 4 ms-1 and 6 ms-1, respectively. They coalesce on impact.
a. Calculate the value of m if the two objects cease to move after impact. [2]
b. Calculate the value of m if they move at 2.4 ms-1 in the direction of B after impact. [2] In fact, m = 18 kg.
c. Calculate the final velocity of the combined mass, making the direction clear. [2]
After a short time, the combined mass breaks apart into two sections with masses 10.5kg and 12 kg. The 10.5 kg section moves in the same direction as the combined mass but with a speed of 1 ms-1. [2]
Medium
Mark as Complete
Mark Scheme
Question 10
Two small smooth spheres A and B of equal radii and of masses 4 kg and m kg respectively, lie on a smooth horizontal plane. Initially, sphere B is at rest and A is moving towards B with speed 6 m s−1. After the collision A moves with the speed of 1.5 m s−1 and B moves with speed 3 m s−1.
Find the two possible values of the loss of kinetic energy due to the collision. [6]
Hard
Mark as Complete
Mark Scheme
Question 11
A railway engine of mass 25000 kg is positioned 50 m behind two carriages, each of mass 15000 kg, which are also 50m apart. The resistances to forward motion are 2kN on the engine and 0.5 kN on each of the carriages. The train is on a straight flat section of the track. The engine begins at rest and starts to produce a driving force of 18kN. As the engine meets the carriages, they instantaneously join together to form a larger train.
Calculate the ϐinal velocity of the engine after it has connected with the second carriage. [6]
Hard
Mark as Complete
Mark Scheme
Question 12
Two particles A and B have masses of 3 kg and 2 kg respectively. They are moving along a straight horizontal line towards each other. Each particle is moving with a speed of 4 ms-1 when they collide.
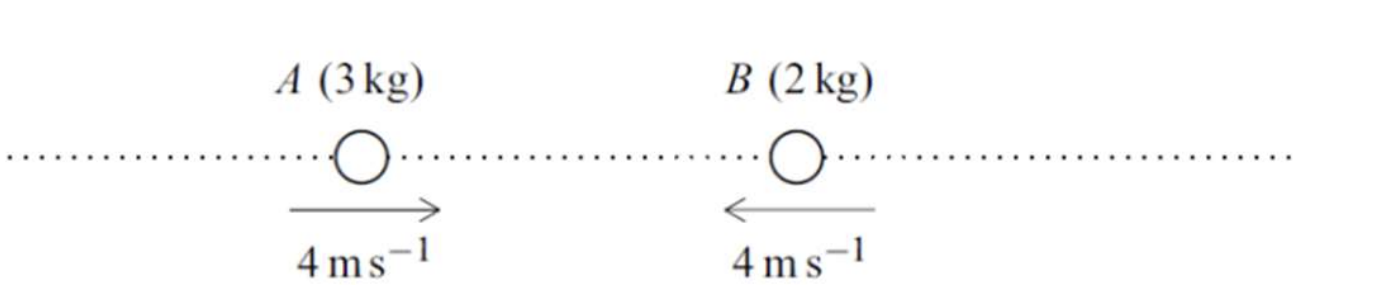
a. If the particles coalesce during the collision to form a single particle, find the speed of the combined particle after the collision. [2]
b. If, after the collision, A moves in the same direction as before the collision with speed 0.4 ms-1, find the speed of B after the collision. [2]
Easy
Mark as Complete
Mark Scheme
Question 13
Two particles P and Q of maqsses 0.2 kg and 0.3 kg respectively are free to move in a horizontal straight line on a smooth horizontal plane. P is projected towards Q with speed 0.5 ms-1.
At the same instant, Q is projected towards P with speed of 1ms-1. Q comes to rest in the resulting collision.
Find the speed of P after the collision. [2]
Easy
Mark as Complete
Mark Scheme
Question 14
Two particles A and B of masses 0.4 kg and 0.2 kg respectively, are moving down the same line of greatest slope of a smooth plane. The plane is inclined at 30o to the horizontal, and A is higher up the plane than B. When the particles collide, the speeds of A and B are 3 ms−1 and 2 ms−1 respectively. In the collision between the particles, the speed of A is reduced to 2.5m s−1.
a. Find the speed of B immediately after the collision. [2]
After the collision, when B has moved 1.6 m down the plane from the point of collision, it hits a barrier and returns up the same line of greatest slope. B hits the barrier 0.4 s after the collision, and when it hits the barrier, its speed is reduced by 90%. The two particles collide again 0.44 s after their previous collision, and they then coalesce on impact.
b. Show that the speed of B immediately after it hits the barrier is 0.5m s−1. Hence find the speed of the combined particle immediately after the second collision between A and B. [7]
Hard
Mark as Complete
Mark Scheme
Question 15
Two particles P and Q of masses 0.3 kg and 0.2 kg respectively, are at rest on a smooth horizontal plane. P is projected at a speed of 4 ms−1 directly towards Q. After P and Q collide, Q begins to move with a speed of 3 ms−1.
a. Find the speed of P after the collision. [2]
After the collision, Q moves directly towards a third particle R, of mass m kg, which is at rest on the plane. The two particles Q and R coalesce on impact and move with a speed of 2 ms−1.
b. Find m. [2]
Easy
Mark as Complete
Mark Scheme
Question 16
Two particles P and Q of masses m kg and 0.3 kg respectively, are at rest on a smooth horizontal plane. P is projected at a speed of 5ms−1 directly towards Q. After P and Q collide, P moves with a speed of 2 ms−1 in the same direction as it was originally moving.
a. Find, in terms of m, the speed of Q after the collision. [2]
After this collision, Q moves directly towards a third particle R, of mass 0.6 kg, which is at rest on the plane. Q is brought to rest in the collision with R, and R begins to move with a speed of 1.5 m s−1.
b. Find the value of m. [2]
Medium
Mark as Complete
Mark Scheme
Question 17
Two particles A and B of masses 3.2 kg and 2.4 kg respectively, lie on a smooth horizontal table. A moves towards B with a speed of v ms−1 and collides with B, which is moving towards A with a speed of 6 ms−1.
a. In the collision, the two particles come to rest. a. Find the value of v [2]
b. Find the loss of kinetic energy of the system due to the collision [2]
Easy
Mark as Complete
Mark Scheme
Question 18
Two particles P and Q of masses 0.1 kg and 0.4 kg respectively, are free to move on a smooth horizontal plane. Particle P is projected with speed 4ms−1 towards Q which is stationary. After P and Q collide, the speeds of P and Q are equal.
Find the two possible values of the speed of P after the collision. [3]
Medium
Mark as Complete
Mark Scheme
Question 19
Two particles P and Q of masses 6 kg and 2 kg respectively, lie at rest 12.5 m apart on a rough horizontal plane. The coefficient of friction between each particle and the plane is 0.4. Particle P is projected towards Q with speed 20 ms−1.
a. Show that the speed of P immediately before the collision with Q is `10sqrt3`ms−1. [3]
In the collision, P and Q coalesce to form particle R.
b. Find the loss of kinetic energy due to the collision. [4]
Hard
Mark as Complete
Mark Scheme
Question 20
A particle A of mass 0.5 kg is projected vertically upwards from horizontal ground with speed 25m s−1.
a. Find the speed of A when it reaches a height of 20 m above the ground. [2]
When A reaches a height of 20 m, it collides with a particle B of mass 0.3 kg which is moving downwards in the same vertical line as A with speed 32.5 ms−1. In the collision between the two particles, B is brought to instantaneous rest.
b. Show that the velocity of A immediately after the collision is 4.5ms−1 downwards. [2]
c. Find the time interval between A and B reaching the ground. You should assume that A does not bounce when it reaches the ground. [4]
Hard
Mark as Complete
Mark Scheme
Question 1
Calculate the momentum of:
a. A tennis ball of mass 0.056kg and velocity 35 ms-1. [1]
b. A piano of mass 160kg falling with a speed of 10 ms-1. [1]
c. A lion of mass 180kg running at a speed of 30kmh-1. [1]
a. p = mv = 0.056x35 = 1.96 kgms-1 [1]
b. p = mv = 160x10 = 1600 kgms-1 [1]
c. Transfer kmh-1 into ms-1, 30 kmh-1 = `30*1000/3600 = 8 1/3`
p = mv = 180x`8 1/3` = 1500 ms-1 [1]
Question 2
Annie and her younger brother Ryan are at the ice rink. They stand facing each other, then Annie pushes against Ryan and they both move backwards. Annie estimates that her movement is 1.5 ms-1.
Given that Annie has mass 40kg and Ryan has mass 30kg, how fast is Ryan moving? [2]
Before and After:
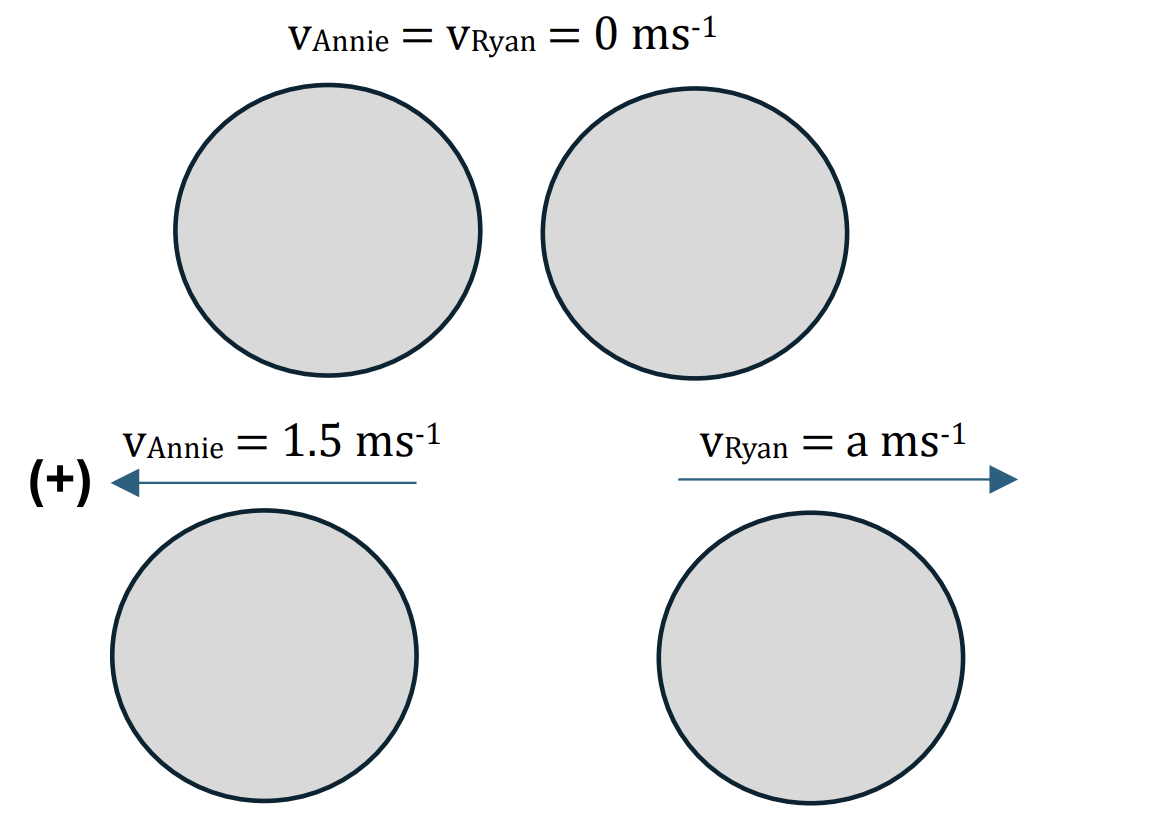
Applying the conservation of linear momentum:
0 = mAnnie`*vec(v_(An nie)) + m_(Ryan)*vec(v_(Ryan))`
Choose positve direction is to the left, we have:
mAnnie.vAnnie – mRyan.vRyan = 0
Annie.vAnnie = mRyan.vRyan
`40*1.5 = 30*a`
`a = frac(40*1.5)(30) = 2` ms-1 [2]
Question 3
Particle P of mass m kg and Q of mass 0.2 kg are free to move on a smooth horizontal plane.
P is projected at a speed of 2 ms-1 towards Q which is stationary. After the collision P and W move in opposite direction with speed of 0.5 ms-1 and 1 ms-1 respectively.
Find m [3]
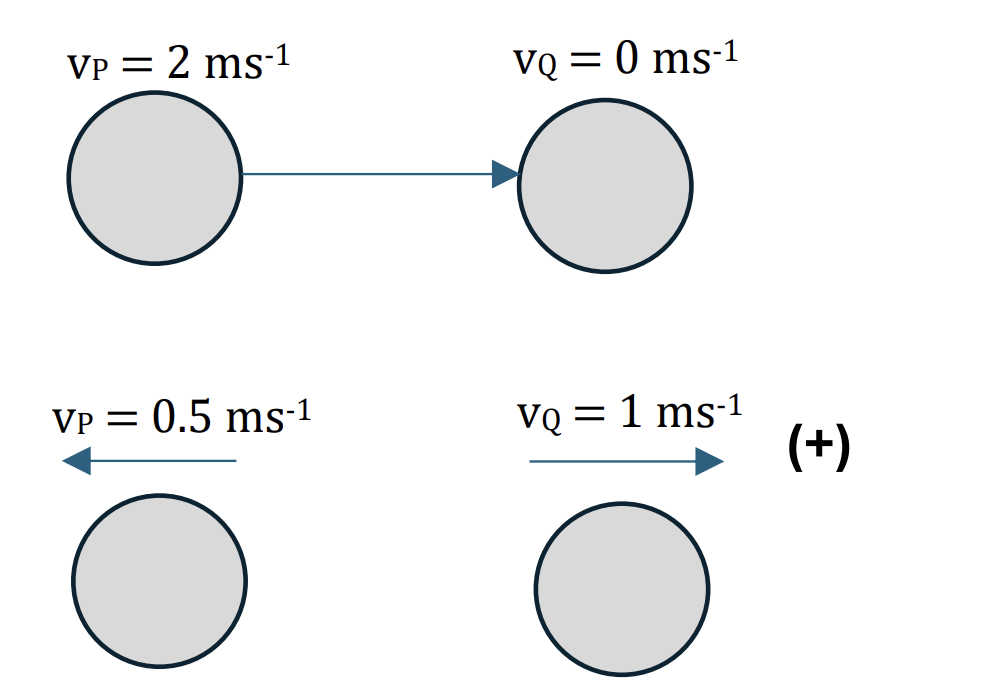
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_p*vec(v_P) + m_Q*vec(v_Q) = m_P*vec(v_P) + m_Q*vec(v_Q)` [1]
Choose positve direction is to the right, we have:
`m_P.v_P + m_Q.v_Q = - m_P.v_P + m_Q.v_Q` [1]
`m_P*2 + 0.2*0 = -m_P*0.5 + 0.2*1`
`m_P = frac(0.2*1)(2.5) = 0.08 ms^-1` [1]
Question 4
Two particles P and Q of masses 0.2kg and 0.5kg respectively, are at rest on smooth horizontal plane. P is projected towards Q with speed 2ms-1.
a. Write down the momentum of P [1]
b. After the collision P continues to move in the same direction with speed 0.3 ms-1.
Find the speed of Q after the collision [2]
a. Momentum = 0.2x2 = 0.4 kgms-1 [1]
b.
Before:
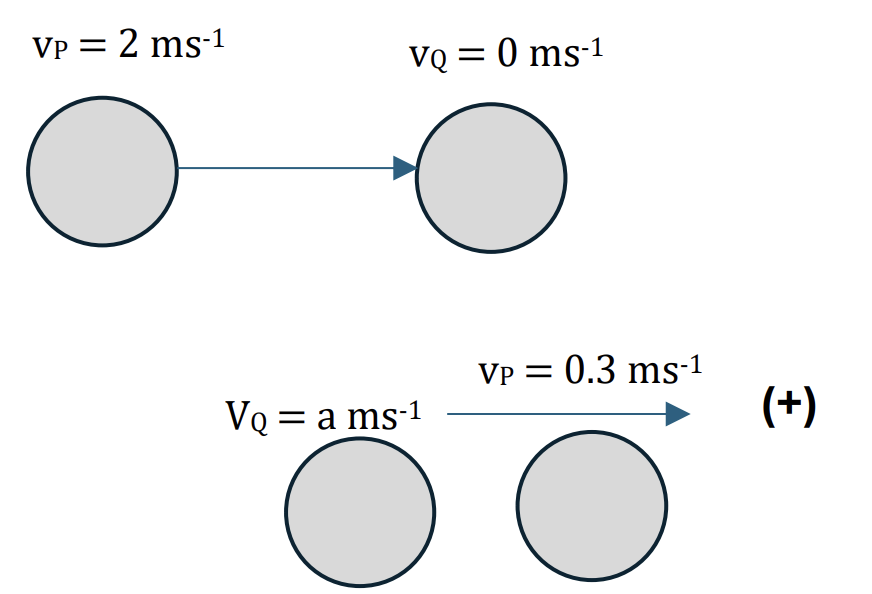
Applying the conservation of linear momentum:
Total in total initial momentum = Total final momentum
`m_P *vec(v_P) + m_Q *vec(v_Q) = m_P *vec(v_P) + m_Q*vec(v_Q)` [1]
Choose positve direction is to the right, we have:
`0.4 + 0 = 0.3*0.2 + 0.5*a`
`a = 0.68 ms^-1 [2]`
Question 5
Ryan makes a cart, which he can jump onto and move, He decides to test it on a smooth, flat road. He stands on it, but it does not move.
We He tries again, jumping from a standing position and landing on the cart with a horizontal speed of 0.5 ms-1. Ryan has a mass of 40 kg and the cart has a mass of 12 kg.
a. Calculate the speed of the cart with Ryan riding on it. [2]
He tries a running start, starting 2m away from the cart and accelerating from rest at a rate of 0.25 ms-2.
b. Calculate the new speed of cart with Ryan riding on it. [3]
He wants the cart to go at a speed of 2ms-1.
c. How far will he have to run at this same rate of acceleration, before jumping into the cart, to achieve this final speed? Is this a realistic situation? [3]
a.
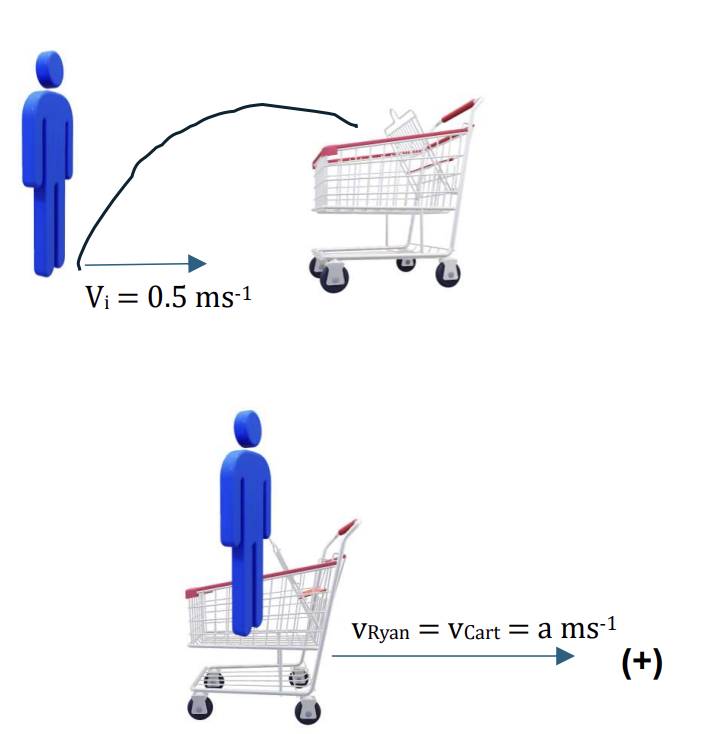
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_R*vec(v_R) + m_C*vec(v_C) = m_R*vec(v_R) + m_C*vec(v_C)` [1]
Choose positve direction is to the right, we have:
`0*0.5 + 0 = 40*a + 12*a`
a = 0.38ms-1
b.
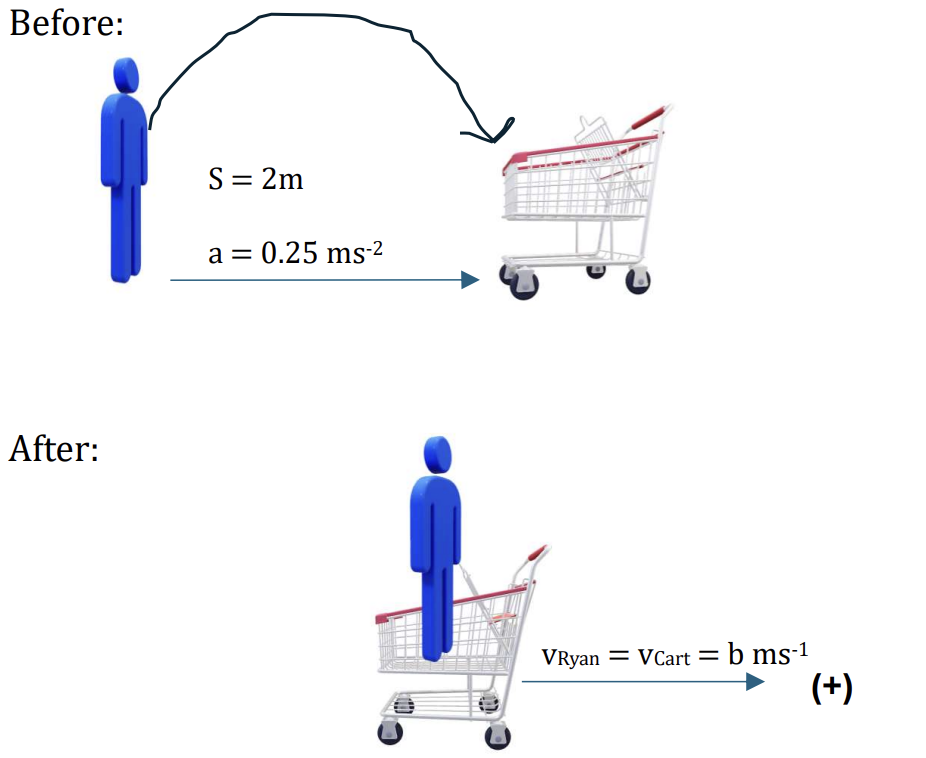
Firstly, calculate the speed when he is running from 2m away, this is intial speed of Ryan.
Using SUVAT equation, we have:
`s = ut + 1/2at^2`
`t = sqrtfrac(2*2)(0.25) = 4`s [1]
v = u + at = `4*0.25` = 1 ms-1
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_R*vec(v_R) + m_C*vec(v_C) = m_R*vec(v_R) + m_C*vec(v_C)` [1]
Choose a positve direction to the right, we have:
`40*1 + 0 = 40*b + 12*b`
`to b = 0.77 ms^-1 [1]`
c.
Find the initial speed of Ryan when he wants the cart to go at a speed of 2ms-1.
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_R*vec(v_R) + m_C*vec(v_C) = m_R*vec(v_R) + m_C*vec(v_C)` [1]
Choose positve direction is to the right, we have:
`40*v_R + 0 = 40*2 + 12*2`
`v_R = 2.6 ms^-1`[1]
Using SUVAT equation, we have:
`v^2 = u^2 + 2as`
`to s = frac(2.6^2 - 0^2)(2*0.25) = 13.52 m`
It is not realistic for Ryan to run for this far at the same acceleration. [1]
Question 6
a. A basketball weighs 13 times more than a golf ball. If they are thrown at each other with an equal and opposite velocity u, show that vg = 12u – 13vb where vg is velocity of the golf ball after impact and vb is the velocity of the basketball after impact. [2]
b. A bullet of mass m kg is fired from a gun of mass M kg, which is free to recoil. Let the initial velocities of the bullet and gun be u ms-1 and U ms-1, respectively.
Show that the initial speeds of the bullet and gun are in inverse ratio to their masses. [3]
a.
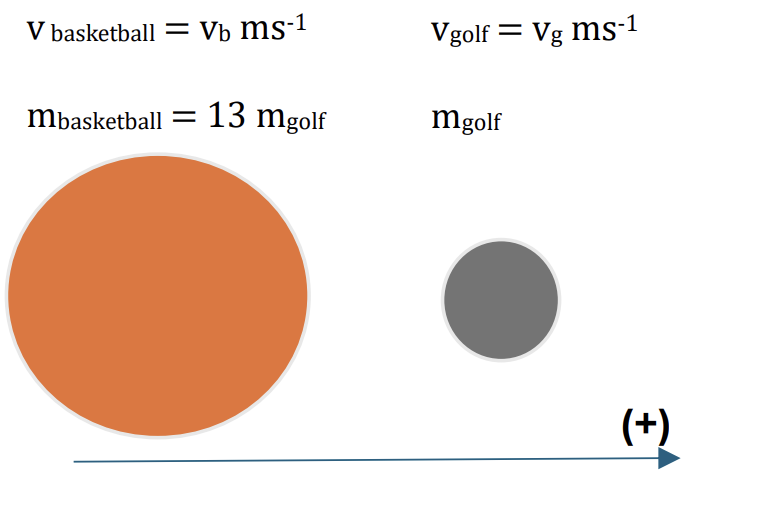
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_(basketball)*vec(v_(basketball)) + m_(golf)*vec(v_(golf)) = m_(basketball)*vec(v_(basketball)) + m_(golf)*vec(v_(golf))` [1]
Choose positive direction is to the right, we have:
13mg.u – mg.u = 13mg.vb + mg.vg (The initial velocity of basketball and golf are opposite and equal. After the collision, the velocity of them the same direction)
So vg = 12u – 13vb [1]
b. Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_(gun)*vec(v_(gun)) + m_(bu ll et)*vec(v_(bu ll et)) = m_(gun)*vec(v_(gun)) + m_(bu ll et)*vec(v_(bu ll et))` [1]`
Choose positive direction is to the right, we have:
`m*u + M*U = 0`(as velocity before ϐiring is zero) [1]
`m * u = - M * U`
`m/M = -U/u`
Because we are comparing speed, not velocity:
`m/M = abs(-U/u)` (required) [1]
Question 7
A bus of mass 10 tonnes is following a car of mass 1.2 tonnes at a distance of 30m. Initially, both are travelling at a constant speed of 36 kmh-1 . The driver’s foot slips and causes the bus to accelerate uniformly. After 5 seconds, the bus crashes into the back of the car, and the two vehicles coalesce.
Find the acceleration (in ms-1) of the bus and the velocity (in kmh-1) of the vehicles immediately after the crash. [5]
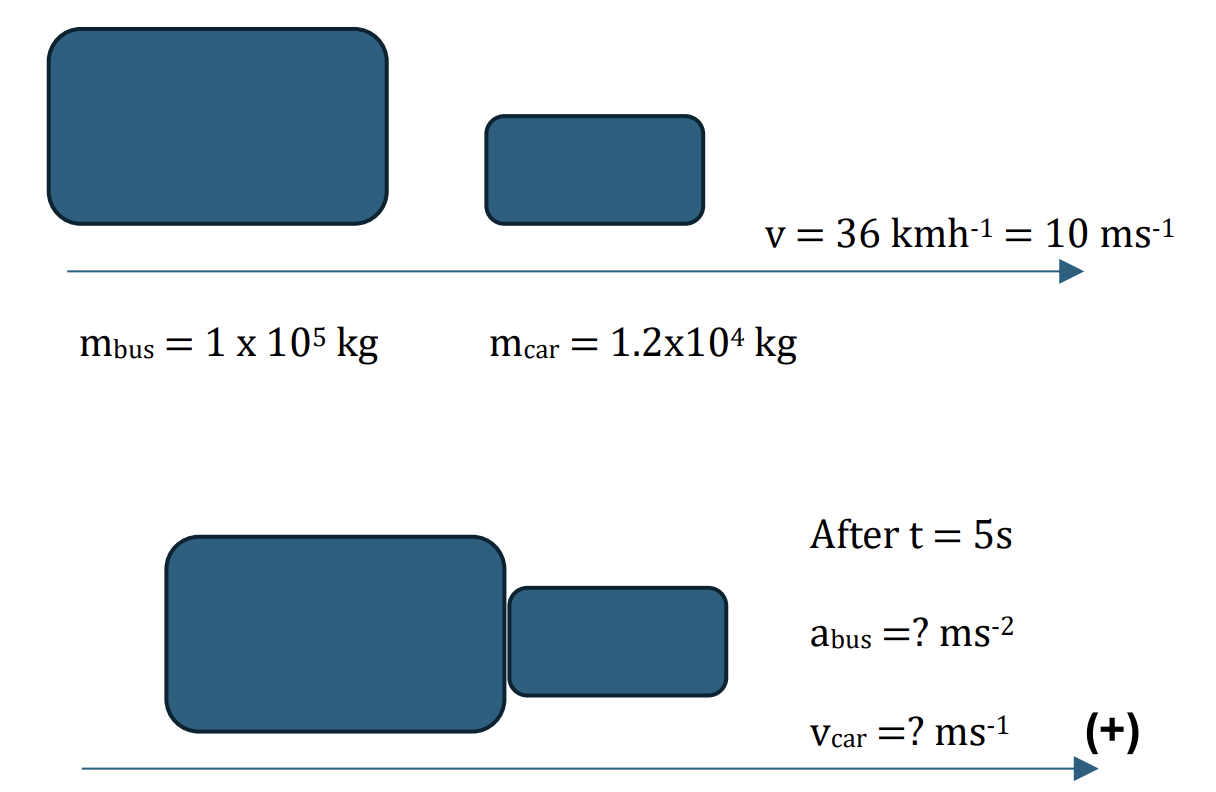
In the 5 seconds the car will travel an extra `10 * 5 = 50 m`. [1]
So for the bus: s = 80, u = 10, v = v, t = 5
`s = (u+v)t/2`
`80 = (10+v)*5/2`
`to v = 22 ms^-1`
v = u + at
22 = 10 + `a*5`
`to a = 2.4 ms^-2`[2]
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_(bus)*vec(v_(bus)) + m_(car)*vec(v_(car)) = m_(bus)*vec(v_(bus)) + m_(car)*vec(v_(car))`
Choose positive direction is to the right, we have:
`1 * 10^5 * 22 + 1200 * 10 = 11200 * v [1]`
`to v = 20.7 ms^-1 = 74.6 kmh^-1. [1]`
Question 8
A particle B of mass 5 kg is at rest on a smooth horizontal table. A particle A of mass 2.5 kg moves on the table with a speed of 6 ms-1 and collides directly with B. In the collision the two particles coalesce.
a. Find the speed of the combined particle after the collision. [2]
b. Find the loss of kinetic energy of the system due to the collision. [3]
a.
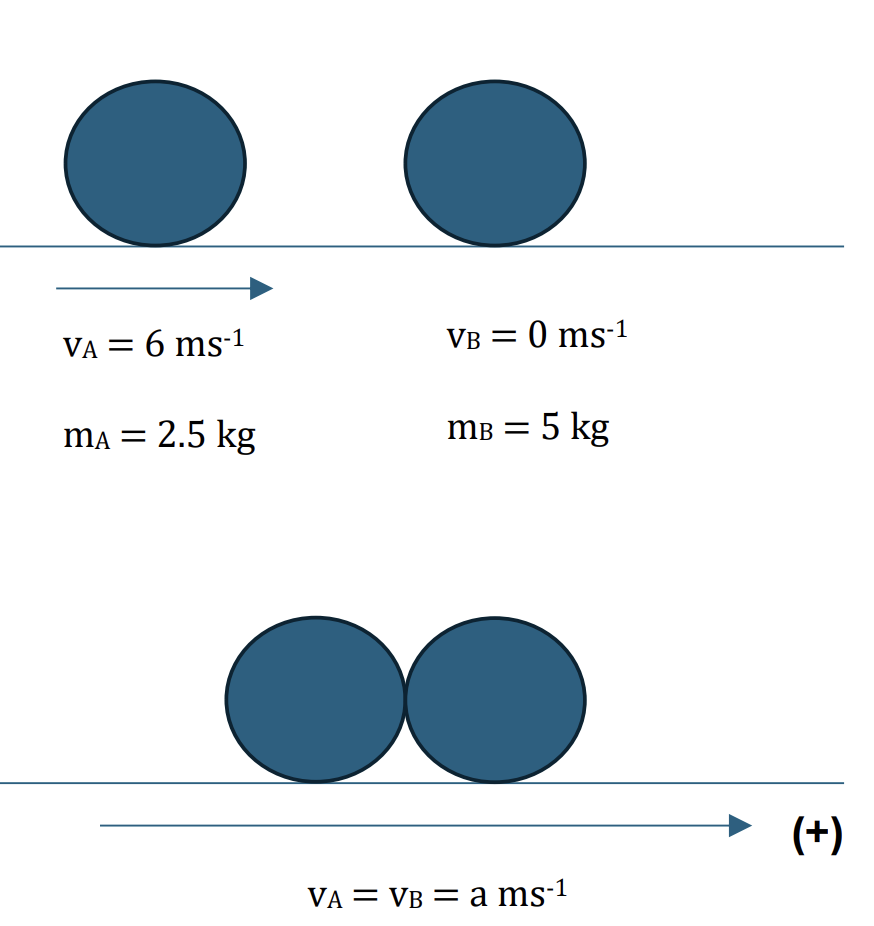
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_B) = m_A*vec(v_A) + m_B*vec(v_B)`
Choose a positive direction is to the right, we have:
`2.5 * 6 + 5 * 0 = (2.5 + 5) * v [1]`
v = 2ms-1 [1]
b. To calculate the loss of kinetic energy of the system due to the collision, we calculate the kinetic energy before and after the collision.
Initial Kinetic energy: KE = `1/2mv^2 = 1/2*2.5*6^2 = 45 J`[1]
Final Kinetic energy: KE = `1/2mv^2 = 1/2*7.5*2^2 = 15J` [1]
`oss of KE = 45 - 15 = 30 J. [1]`
Question 9
Two objects A and B of mass 4.5kg and m kg approach each other at speeds of 4 ms-1 and 6 ms-1, respectively. They coalesce on impact.
a. Calculate the value of m if the two objects cease to move after impact. [2]
b. Calculate the value of m if they move at 2.4 ms-1 in the direction of B after impact. [2] In fact, m = 18 kg.
c. Calculate the final velocity of the combined mass, making the direction clear. [2]
After a short time, the combined mass breaks apart into two sections with masses 10.5kg and 12 kg. The 10.5 kg section moves in the same direction as the combined mass but with a speed of 1 ms-1. [2]
a.
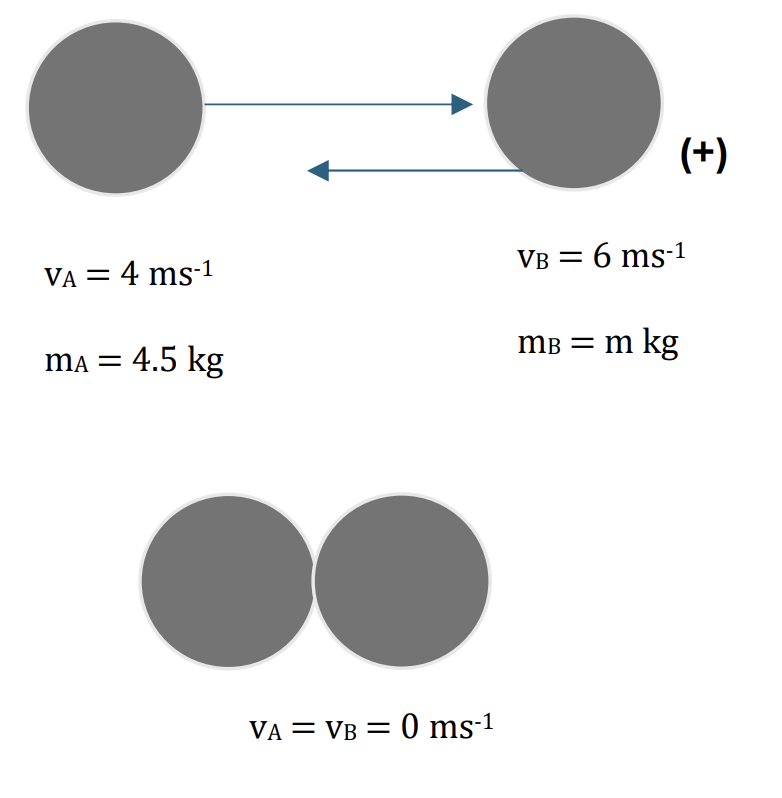
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_A) + m_B*vec(v_B)` [1]
Choose positve direction is to the right, we have:
`4.5 * 4 – 6 * m = 0`
m = 3 kg [1]
b. Before
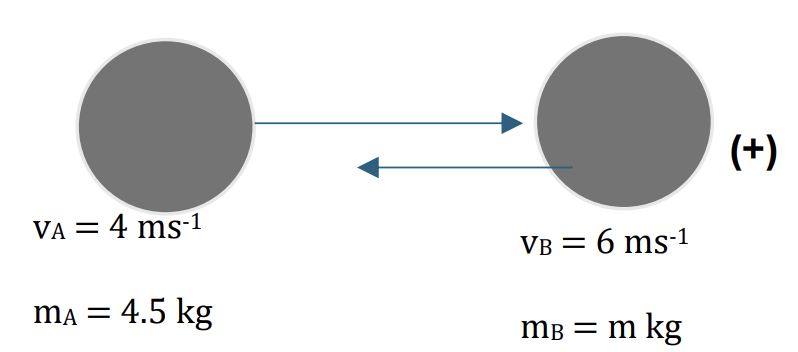
After

Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_A) + m_B*vec(v_B)` [1]
Choose the positive direction is to the left, we have:
`4.5 * 4 + 6 * m = (4.5+m) * 2.4`
m = 8kg [1]
c. Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_A) + m_B*vec(v_B)` [1]
Choose the positve direction is to the left, we have:
`-4.5 * 4 + 18 * 6 = 22.5 * v`
v = 4 ms-1, given the direction, is the same as object B [1]
Question 10
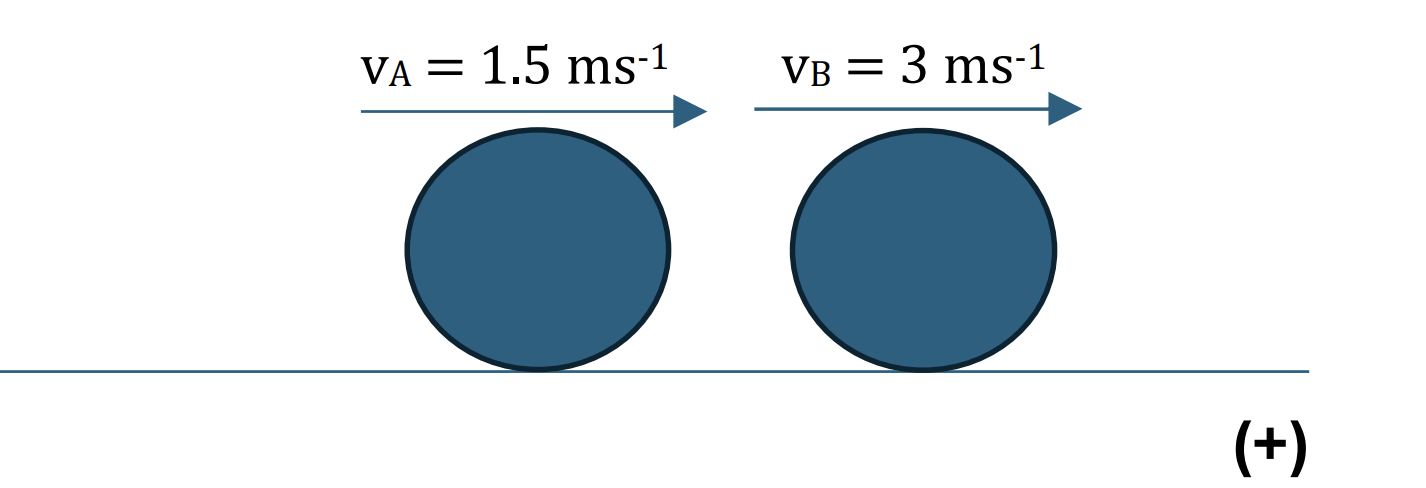
Two small smooth spheres A and B of equal radii and of masses 4 kg and m kg respectively, lie on a smooth horizontal plane. Initially, sphere B is at rest and A is moving towards B with speed 6 m s−1. After the collision A moves with the speed of 1.5 m s−1 and B moves with speed 3 m s−1.
Find the two possible values of the loss of kinetic energy due to the collision. [6]
Before:
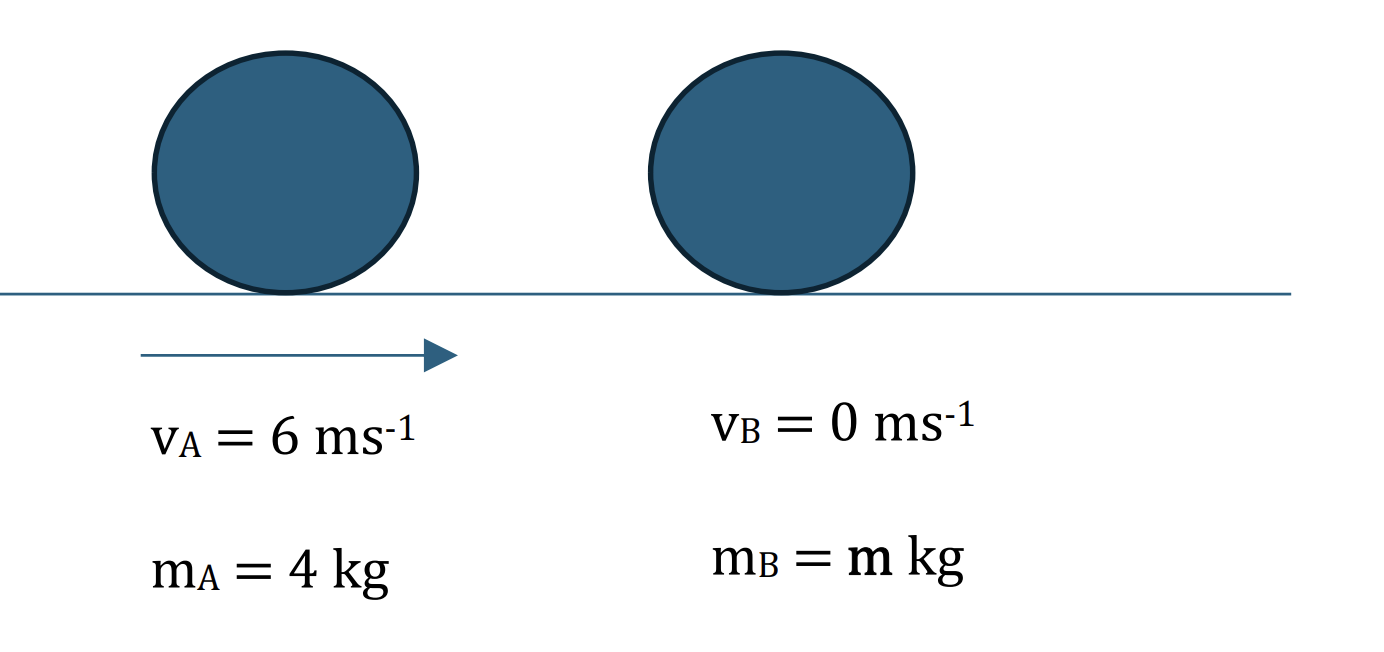
There are two predictions of the direction of B after the collision. [1]
After:
Applying the conservation of linear momentum:
Total intial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_B) = m_A *vec(v_A) + m_B*vec(v_B)`
Choose positive direction is to the right, we have: (B has the same direction to A)
`4 8 6 + m * 0 = 4 * 1.5 + m * 3`
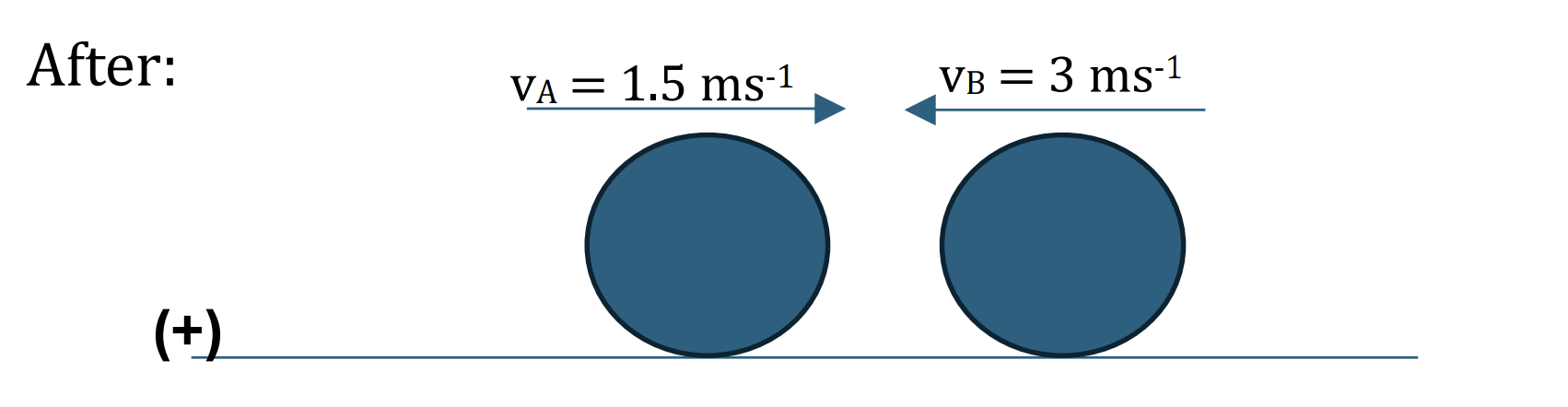
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_B) = m_A *vec(v_A) + m_B*vec(v_B)`
Choose the positve direction is to the left, we have: (B has the opposite direction to A)
`4 * 6 + m * 0 = m * 3 - 4 * 1.5`
m = 10 kg [1]
To calculate the loss of kinetic energy due to the collision, we have:
Initial kinetic energy of A: KEAA(i) = `1/2 m*v^2 = 1/2*4*6^2 = 72 J`
Final kinetic energy of A: KEA(F) = `1/2 m*v^2 = 1/2*4*1.5^2 = 4.5 J`
Final kinetic energy of B: KEB(F)`= 1/2 m*v^2 = 1/2*6*3^2 = 27 J`
Or final kinetic energy of B: KEB(F) = `1/2 m*v^2 = 1/2*10*3^2 = 45 J [3]`
KE loss = `1/2*4*6^2 - 1/2*4*1.5^2 - 1/2*6*3^2= 40.5 J`
Or KE loss = `1/2*4*6^2 - 1/2*4*1.5^2 - 1/2*10*3^2= 22.5 J [3]`
Question 11
A railway engine of mass 25000 kg is positioned 50 m behind two carriages, each of mass 15000 kg, which are also 50m apart. The resistances to forward motion are 2kN on the engine and 0.5 kN on each of the carriages. The train is on a straight flat section of the track. The engine begins at rest and starts to produce a driving force of 18kN. As the engine meets the carriages, they instantaneously join together to form a larger train.
Calculate the ϐinal velocity of the engine after it has connected with the second carriage. [6]
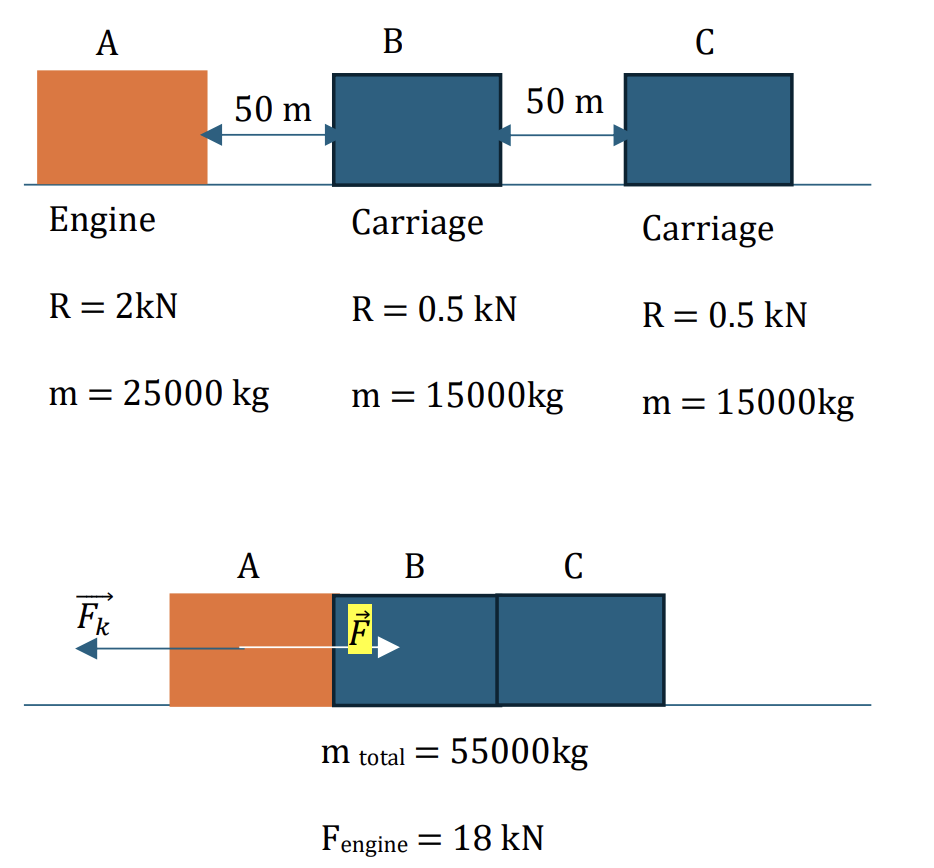
A moves to B:
`vec(F_(dri v i n g f o r c e)) + vec(F_k) = vec(F_(n e t))` (as the forces are equilibrium)
Choose positive direction is moving to the right, we have:
Fdriving force - Fk = ma
So a = `frac(18000-2000)(25000) = 0.64 ms^-2` [1]
Applying SUVAT equation with s = 50 m, u = 0 ms-1
v2 – u2 = 2as
`to v = sqrt(2*0.64*50) = 8 ms^-1`. This is velocity when A meets B [1]
At A is joining to B, applying the conservation of linear momentum:
`25000 * 8 = (25 000 + 15 000) *v_1`
`→ v_1 = 5 ms^(-1) [1]`
So `v_1 = 5 ms^(-1)` is velocity of both A and B joined.
AB is moving to C:
`vec(F_(dri v i n g f o r c e)) + vec(F_k) = vec(F_(n e t))` (as the forces are equilibrium)
Choose positive direction is moving to the right, we have:
Fdriving force - Fk = ma
So a = `frac(18000-2500)(40000) = 0.3875 ms^-2` [1]
Applying SUVAT equation with s = 50 m, u = v1 = 5 ms-1,
`v_2 – u_2 = 2as`
`→ v2 = sqrt(2 * 0.64 * 50 + 25 ) =sqrt(63.75` ms-1. This is velocity when AB meets C [1]
At AB joins to C:
`40000 × sqrt(63.75) = 55000 * v_3`
So v3 = 5.81 ms-1 [1]
Question 12
Two particles A and B have masses of 3 kg and 2 kg respectively. They are moving along a straight horizontal line towards each other. Each particle is moving with a speed of 4 ms-1 when they collide.

a. If the particles coalesce during the collision to form a single particle, find the speed of the combined particle after the collision. [2]
b. If, after the collision, A moves in the same direction as before the collision with speed 0.4 ms-1, find the speed of B after the collision. [2]

a. Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_B)= m_A*vec(v_A) + m_B*vec(v_B)`
Choose positve direction is to the right, we have: (B has the same direction to A)
`3 * 4 + 2 * -4 = 5 * v [1]`
`v = 0.8 ms^(-1)`
The direction of velocity that combined particle after collision is moving follow direction of particle A. [1]
b. After the collision:
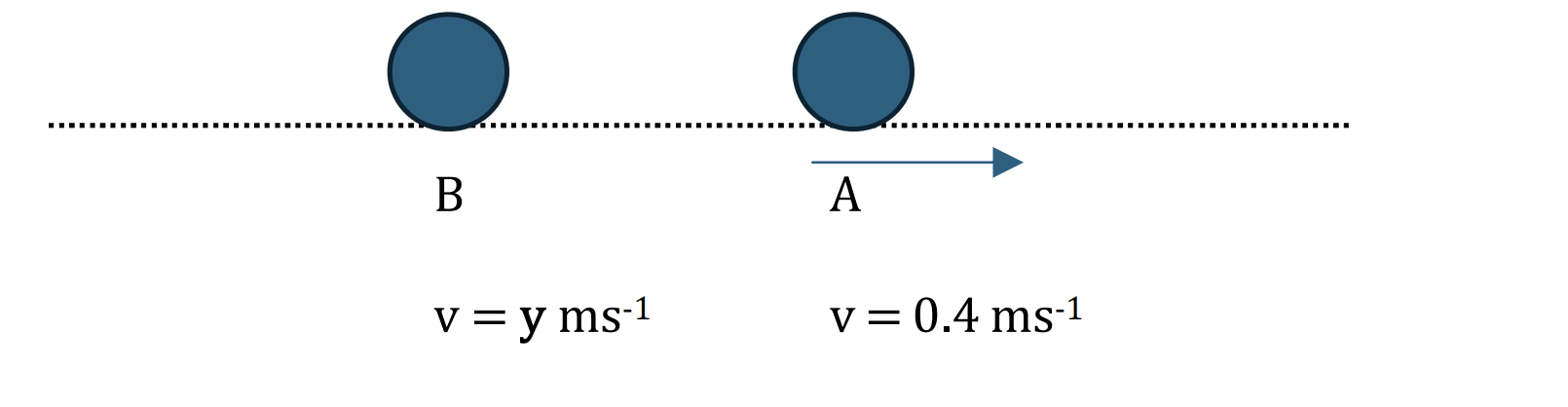
B moves to the same direction of A
Applying the conservation of linear momentum:
Total intial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_B)= m_A*vec(v_A) + m_B*vec(v_B)`
Choose a positve direction is to the right, we have:
`3 * 4 + 2 * -4 = 3 * 0.4 + 2 * y [1]`
y = 1.4 ms-1 [1]
Question 13
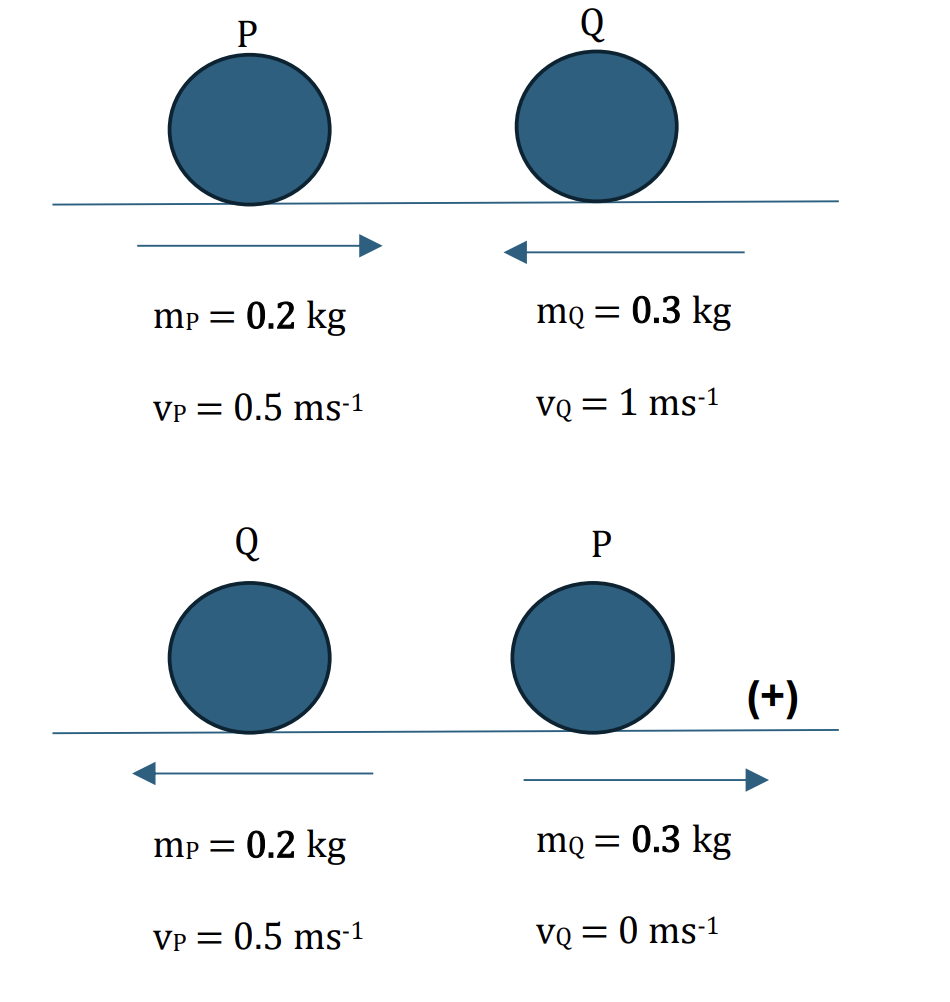
Two particles P and Q of maqsses 0.2 kg and 0.3 kg respectively are free to move in a horizontal straight line on a smooth horizontal plane. P is projected towards Q with speed 0.5 ms-1.
At the same instant, Q is projected towards P with speed of 1ms-1. Q comes to rest in the resulting collision.
Find the speed of P after the collision. [2]
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_P*vec(v_P) + m_Q*vec(v_Q) = m_P*vec(v_P) + m_Q*vec(v_Q)`
Choose the positive direction is to the left, we have:
`0.2 * -0.5 + 0.3 * 1 = 0.3 * 0 + 0.2 * v [1]`
Speed = 1 ms-1. The speed of P after the collision is 1 ms-1. [1]
Question 14
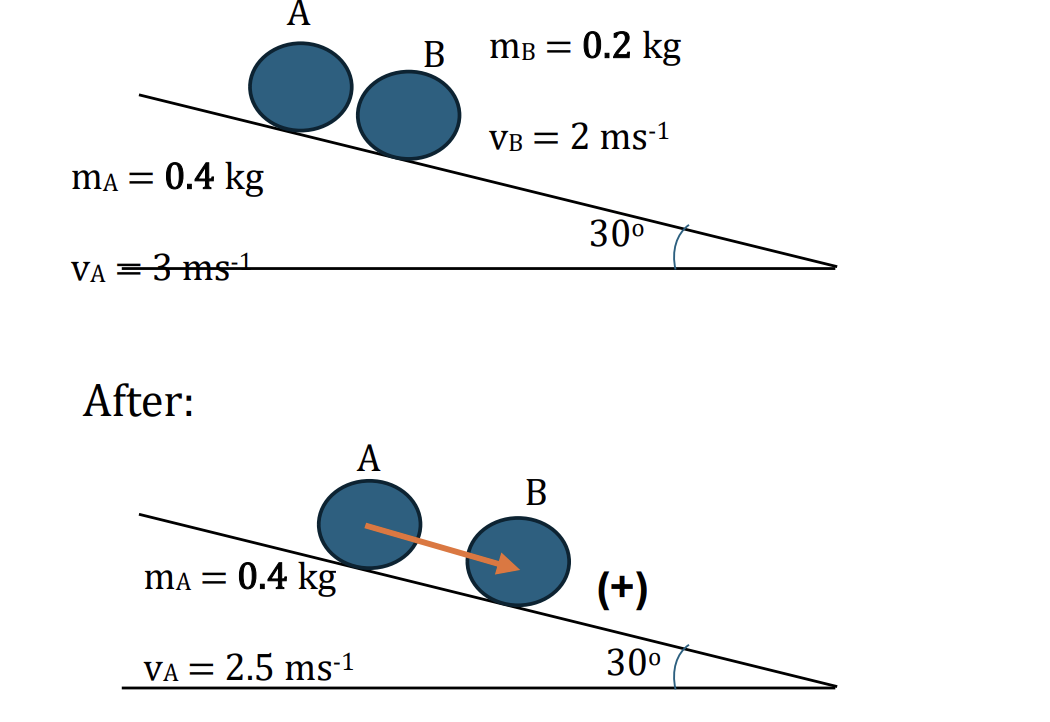
Two particles A and B of masses 0.4 kg and 0.2 kg respectively, are moving down the same line of greatest slope of a smooth plane. The plane is inclined at 30o to the horizontal, and A is higher up the plane than B. When the particles collide, the speeds of A and B are 3 ms−1 and 2 ms−1 respectively. In the collision between the particles, the speed of A is reduced to 2.5m s−1.
a. Find the speed of B immediately after the collision. [2]
After the collision, when B has moved 1.6 m down the plane from the point of collision, it hits a barrier and returns up the same line of greatest slope. B hits the barrier 0.4 s after the collision, and when it hits the barrier, its speed is reduced by 90%. The two particles collide again 0.44 s after their previous collision, and they then coalesce on impact.
b. Show that the speed of B immediately after it hits the barrier is 0.5m s−1. Hence find the speed of the combined particle immediately after the second collision between A and B. [7]
a. Before:
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A)+ m_B*vec(v_B) = m_A*vec(v_A)+ m_B*vec(v_B)`
Choose a positve direction is to the right, we have:
`0.4 * 3 + 0.2 * 2 = 0.4 * 2.5 + 0.2 * v [1]`
v = 3 ms-1. The speed of B after the collision is 3 ms-1 [1]
b.
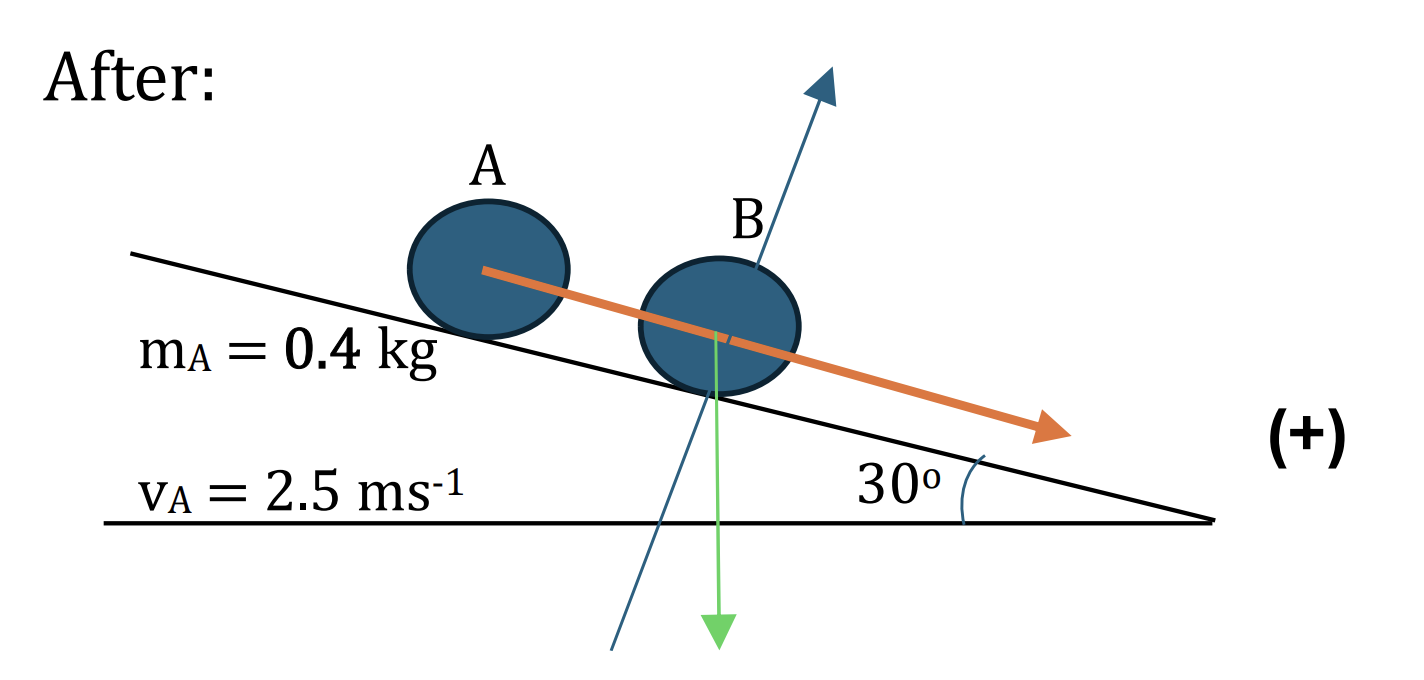
At point B, we have force equilibrium as
`F_(net) = ± mgsin30^o`
`to ma = ±0.2x9.8.sin30^o`
`to → a = 5 ms^(-2) [2]`
For B when hits barrier `v^2 = 32 +2*5*1.6`
`to v = 5ms^-1 [1]`
Speed after hitting barrier = `0.1*5 = 0.5 ms^(-1)`
`v_A = 2.5 + 5*0.44 = 4.7 ms^(-1) [1]`
`v_B = -0.5 + 5*0.04 = -0.3 ms^(-1) [1]`
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_B) = m_A*vec(v_A) + m_B*vec(v_B)`
`0.4 * 4.7 + 0.2 * (-0.3) = 0.6 * v_(combo`
`V_(combo) = 3.03 ms^(-1) [2]`
Question 15
Two particles P and Q of masses 0.3 kg and 0.2 kg respectively, are at rest on a smooth horizontal plane. P is projected at a speed of 4 ms−1 directly towards Q. After P and Q collide, Q begins to move with a speed of 3 ms−1.
a. Find the speed of P after the collision. [2]
After the collision, Q moves directly towards a third particle R, of mass m kg, which is at rest on the plane. The two particles Q and R coalesce on impact and move with a speed of 2 ms−1.
b. Find m. [2]
a.
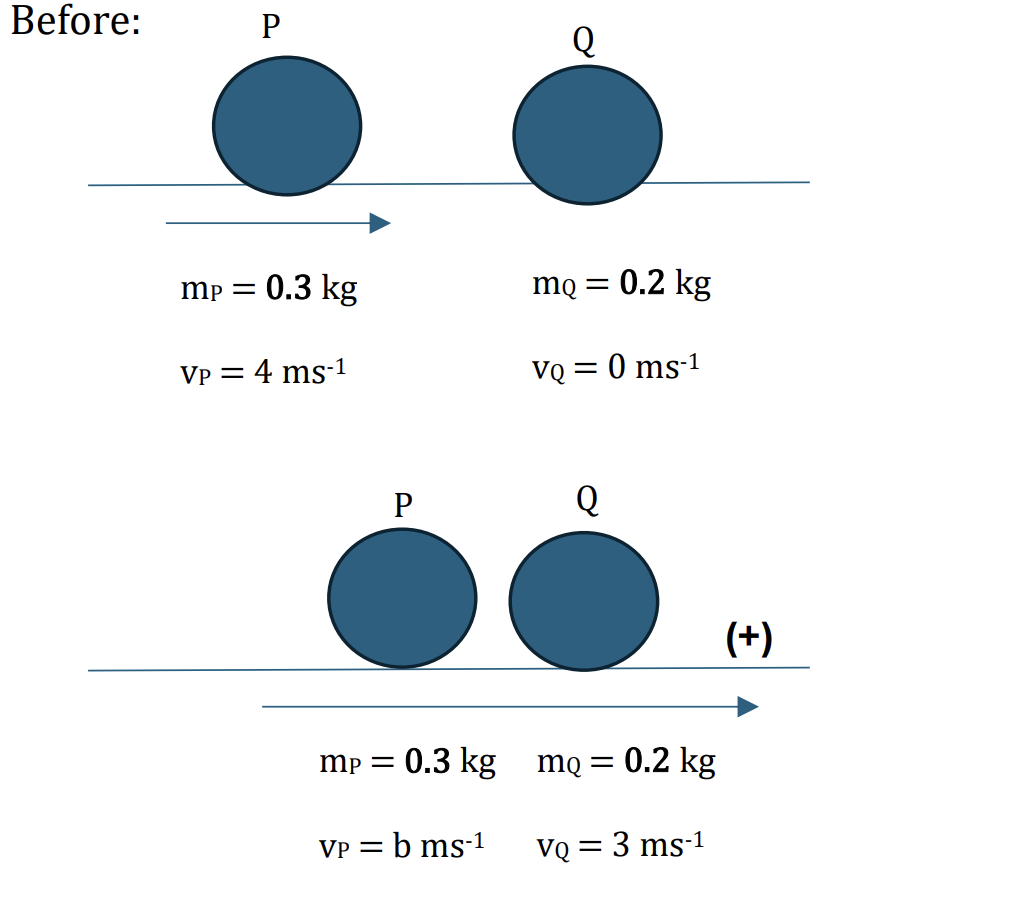
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_P*vec(v_P) + m_Q*vec(v_Q) = m_P*vec(v_P) + m_Q*vec(v_Q)`
Choose a positve direction is to the right, we have:
`0.3 * 4 + 0.2 * 0 = 0.3 * b + 0.2 * 3`
b = 2 ms-1. So the speed of P after the collision is 2 ms-1. [2]
b.
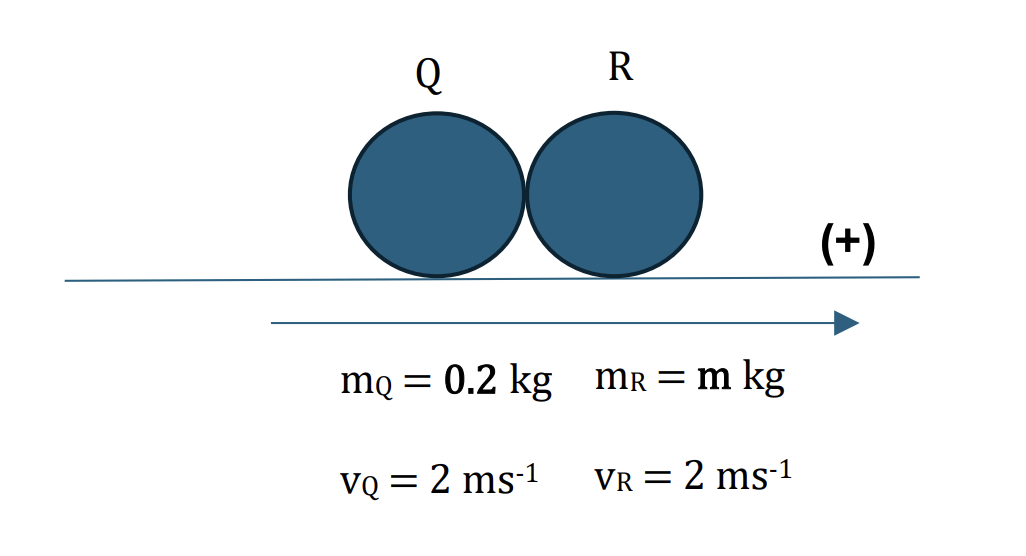
Applying the conservation of linear momentum:
Total intial momentum = Total final momentum
`m_Q*vec(v_Q) + m_R*vec(v_R) = m_Q*vec(v_Q) + m_R*vec(v_R)`
Choose positve direction is to the right, we have:
`.2 * 3 + m * 0 = 0.2 * 2 + 2 * m`
`to m = 0.1 kg [2]`
Question 16
Two particles P and Q of masses m kg and 0.3 kg respectively, are at rest on a smooth horizontal plane. P is projected at a speed of 5ms−1 directly towards Q. After P and Q collide, P moves with a speed of 2 ms−1 in the same direction as it was originally moving.
a. Find, in terms of m, the speed of Q after the collision. [2]
After this collision, Q moves directly towards a third particle R, of mass 0.6 kg, which is at rest on the plane. Q is brought to rest in the collision with R, and R begins to move with a speed of 1.5 m s−1.
b. Find the value of m. [2]
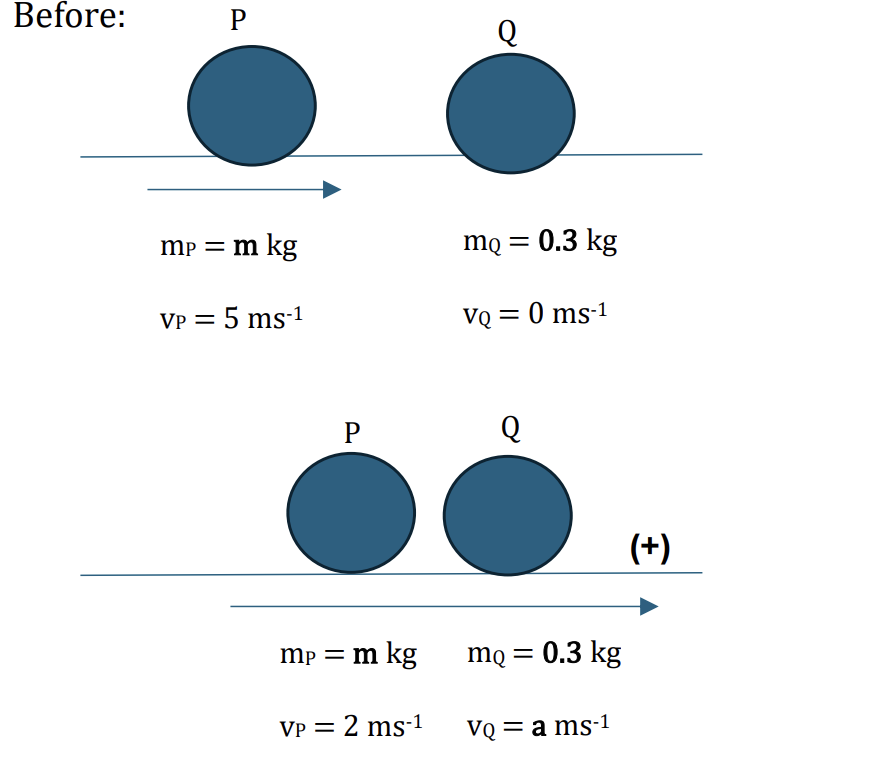
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_P*vec(v_P) + m_Q*vec(v_Q) = m_P*vec(v_P) + m_Q*vec(v_Q)`
Choose positive direction is to the right, we have:
`m * 5 + 0.3 * 0 = m * 2 + a * 0.3`
`a = 10m ms^(-1) [2]`
b.
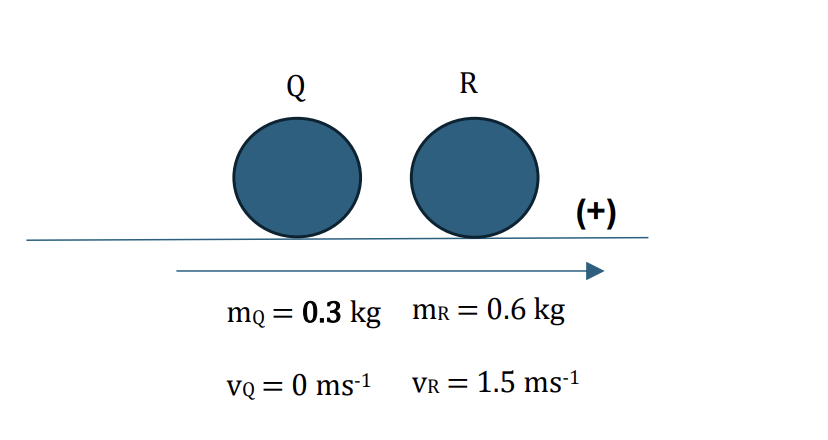
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_Q*vec(v_Q) + m_Rvec(v_R) = m_Q*vec(v_Q) + m_R*vec(v_R)`
Choose positive direction is to the right, we have:
`0.3 * 10m + 0.6 * 0 = 0.6 * 1.5 + 0.3 * 0`
m = 0.3 kg [2]
Question 17
Two particles A and B of masses 3.2 kg and 2.4 kg respectively, lie on a smooth horizontal table. A moves towards B with a speed of v ms−1 and collides with B, which is moving towards A with a speed of 6 ms−1.
a. In the collision, the two particles come to rest. a. Find the value of v [2]
b. Find the loss of kinetic energy of the system due to the collision [2]
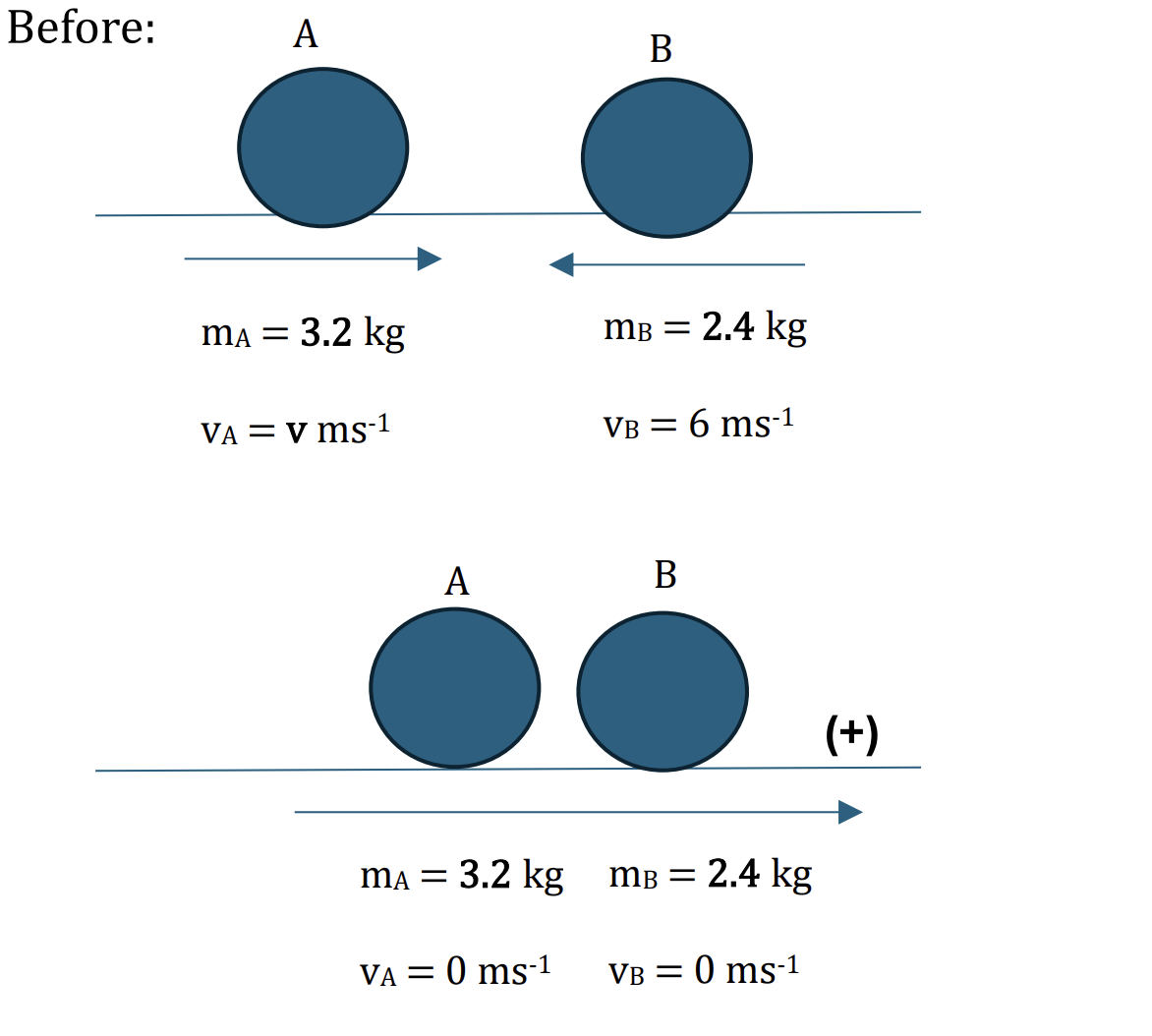
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_B) = m_A*vec(v_A) + m_B*vec(v_B)`
Choose a positive direction is to the right, we have:
`3.2 * v - 2.4 * 6 = (3.2 + 2.4) * 0`
v = 4.5 ms-1 [2]
b.
The loss of kinetic energy of the system due to the collision
Total initial kinetic energy = total final kinetic energy KEA + KEB = 0 + Loss of energy
So loss of energy = `1/2m(v_A)^2 + 1/2m(v_B)^2`
KEloss of energy = `1/2 *3.2*(4.5)^2 + 1/2 *2.4*(6)^2`
KEloss of energy = 75.6 J [2]
Question 18
Two particles P and Q of masses 0.1 kg and 0.4 kg respectively, are free to move on a smooth horizontal plane. Particle P is projected with speed 4ms−1 towards Q which is stationary. After P and Q collide, the speeds of P and Q are equal.
Find the two possible values of the speed of P after the collision. [3]
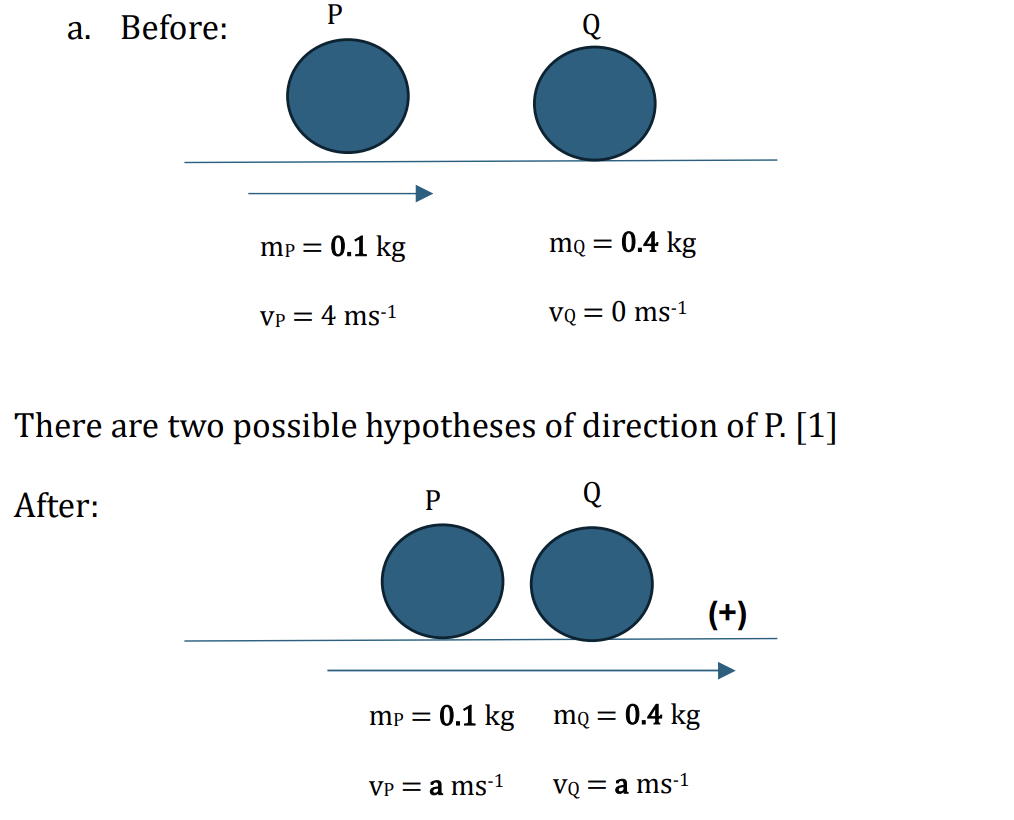
Hypothesis 1: P and Q has the same direction Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_P*vec(v_P) + m_Q*vec(v_Q) = m_P*vec(v_P) + m_Q*vec(v_Q`
Choose positve direction is to the right, we have:
`0.1 * 4 + 0.4 * 0 = (0.1 + 0.4) * a`
`a =0.8 ms^(-1) [1]`
Hypothesis 2: P and Q have the opposite direction
There are two possible hypotheses of the direction of P. [1]
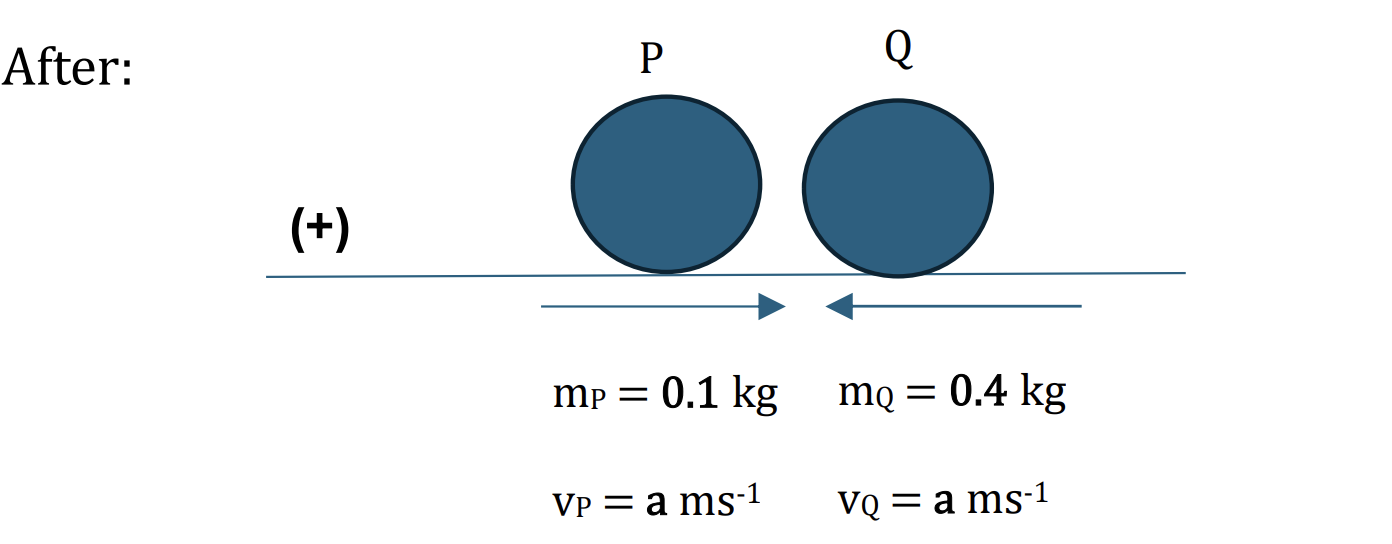
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_P*vec(v_P) + m_Q*vec(v_Q) = m_P*vec(v_P) + m_Q*vec(v_Q`
Choose the positive direction is to the left, we have:
`0.1 * 4 + 0.4 * 0 = (- 0.1 + 0.4) *a`
`a = 1.33 ms^(-1) [1]`
Question 19
Two particles P and Q of masses 6 kg and 2 kg respectively, lie at rest 12.5 m apart on a rough horizontal plane. The coefficient of friction between each particle and the plane is 0.4. Particle P is projected towards Q with speed 20 ms−1.
a. Show that the speed of P immediately before the collision with Q is `10sqrt3`ms−1. [3]
In the collision, P and Q coalesce to form particle R.
b. Find the loss of kinetic energy due to the collision. [4]
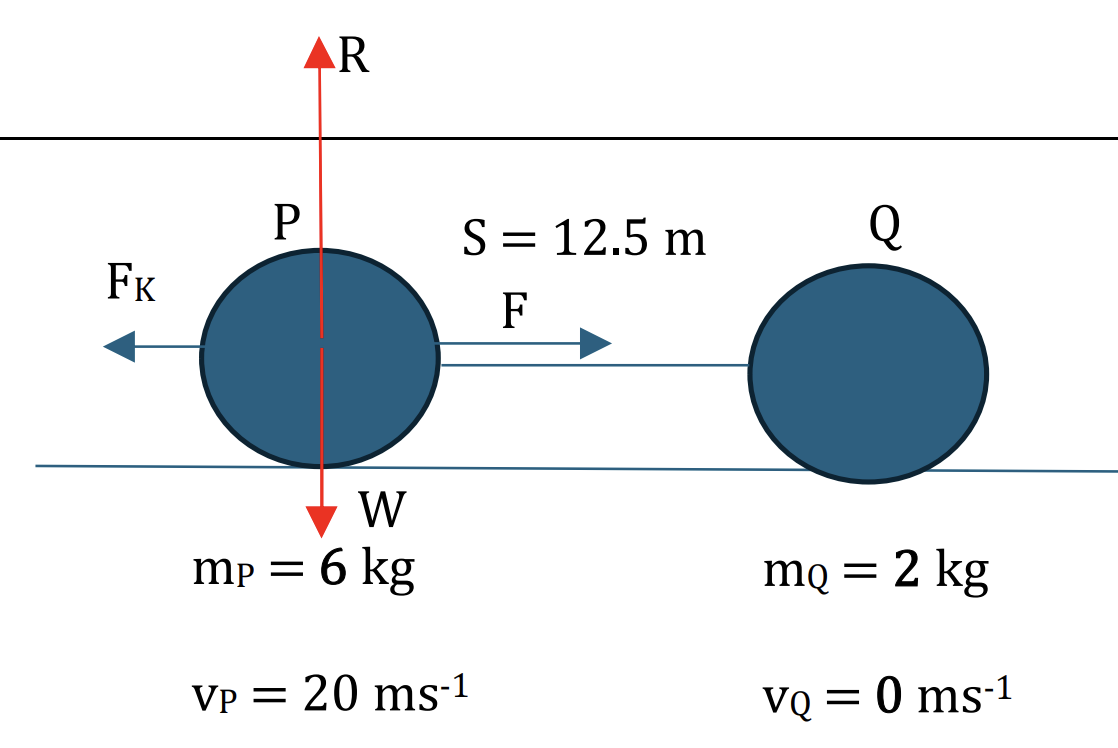
At point P, the force is equilibrium, so we have:
`F_(n et = - muR = - mu * W = - mu * m * g (R = W)`
`6 * a = - 0.4 * 10 * 6`
`a = 0.4 * 10= - 4 ms^(-2)`
Using SUVAT equation, we have:
`v^2 - u^2 = 2 * a * s (a = - 4 ms^(-2))`
`v = sqrt(2as + u^2) = sqrt((2 * (-4) * 12.5 + 20^2)) = 10sqrt3 ms^(-1)` (shown)
*Alternative answer:
KEfinal - KEintial = Work
`1/2 mv^2 - 1/2 mu^2 = Fdcostheta`
`1/2 * 6 * v^2 - 1/2* 6 * 20^2 = - 0.4 * 10 * 6 * 12.5`
v = `10sqrt3`
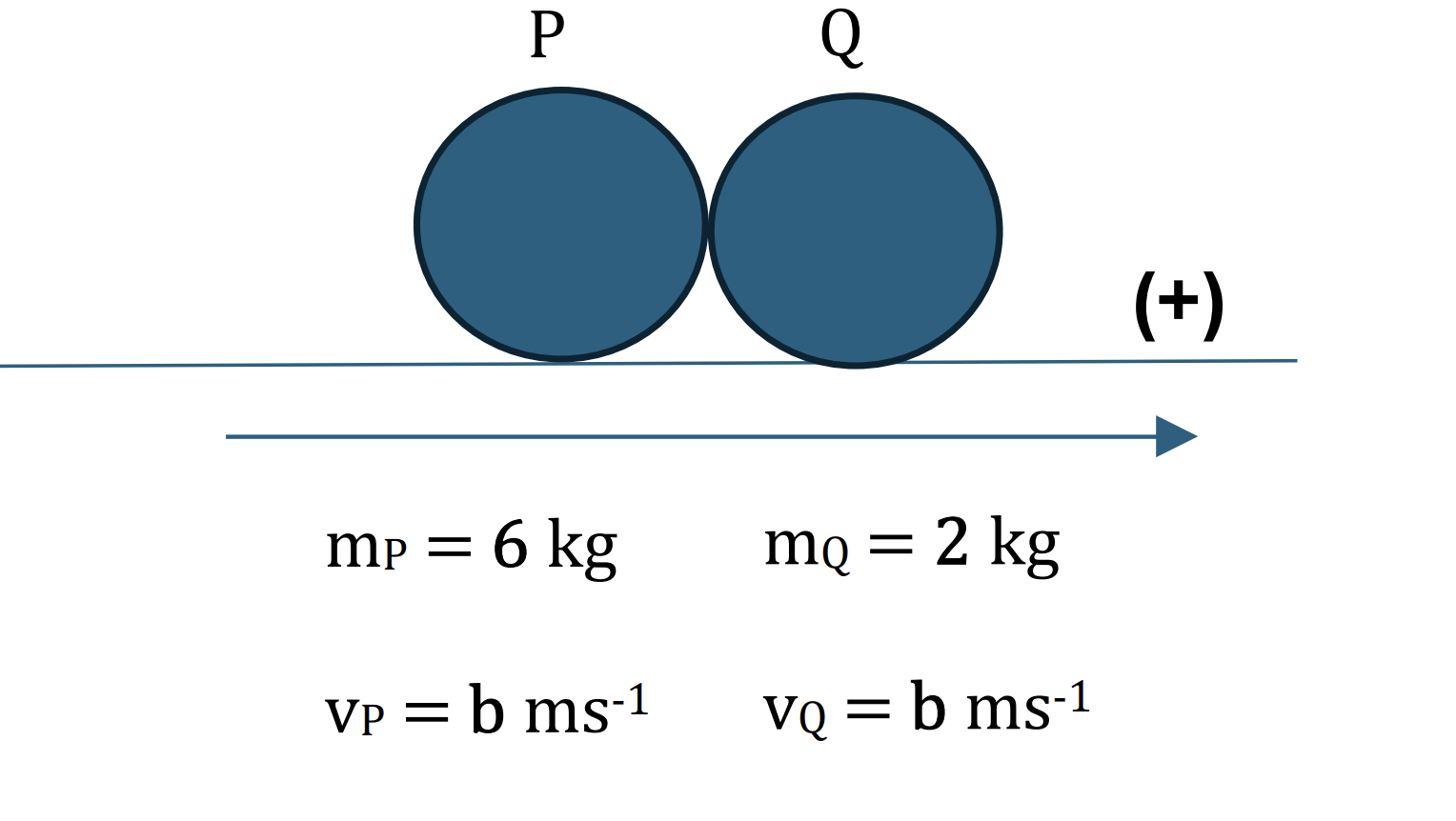
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_P*vec(v_P) + m_Q*vec(v_Q) = m_P*vec(v_P) + m_Q*vec(v_Q)`
Choose a positve direction is to the right, we have:
`6 * 10sqrt3 + 2 * 0 = (6 + 2) * b`
`b = 7.5sqrt3 ms^(-1`
The loss of energy = KEintital - KEfinal
Loss of energy = `1/2 mv^2 - 1/2mb^2`
Loss of energy = `1/2*6*(10sqrt3) - 1/2*8*(7.5sqrt3)`
Loss of energy = 225 J [2]
Question 20
A particle A of mass 0.5 kg is projected vertically upwards from horizontal ground with speed 25m s−1.
a. Find the speed of A when it reaches a height of 20 m above the ground. [2]
When A reaches a height of 20 m, it collides with a particle B of mass 0.3 kg which is moving downwards in the same vertical line as A with speed 32.5 ms−1. In the collision between the two particles, B is brought to instantaneous rest.
b. Show that the velocity of A immediately after the collision is 4.5ms−1 downwards. [2]
c. Find the time interval between A and B reaching the ground. You should assume that A does not bounce when it reaches the ground. [4]
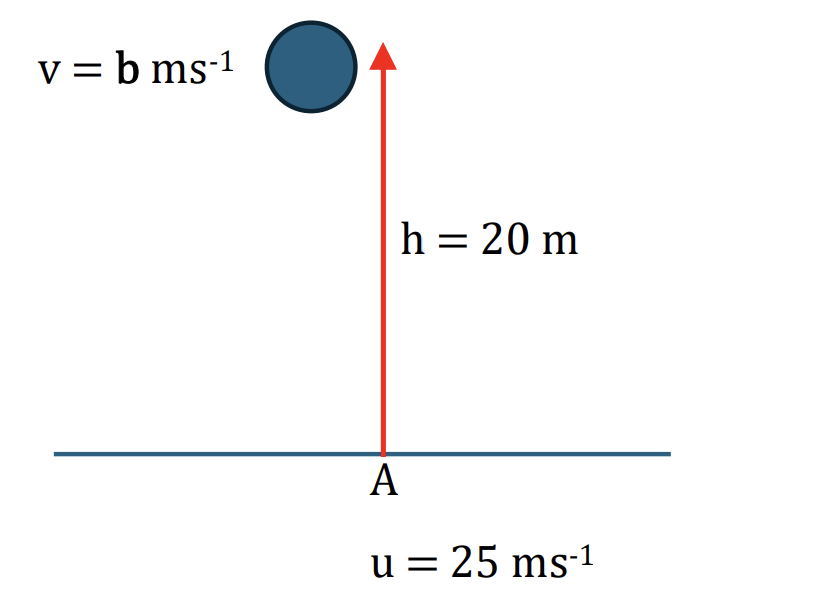
Using SUVAT equation, we have:
`v^2 – u^2 = 2as` (therefore a = -g = -10 ms-2)
`b^2 – 25^2 = 2 *-10 * 20`
`b = sqrt(25^2 + 2 * -10 * 20) = 15 ms^(-1) [2]`
b.
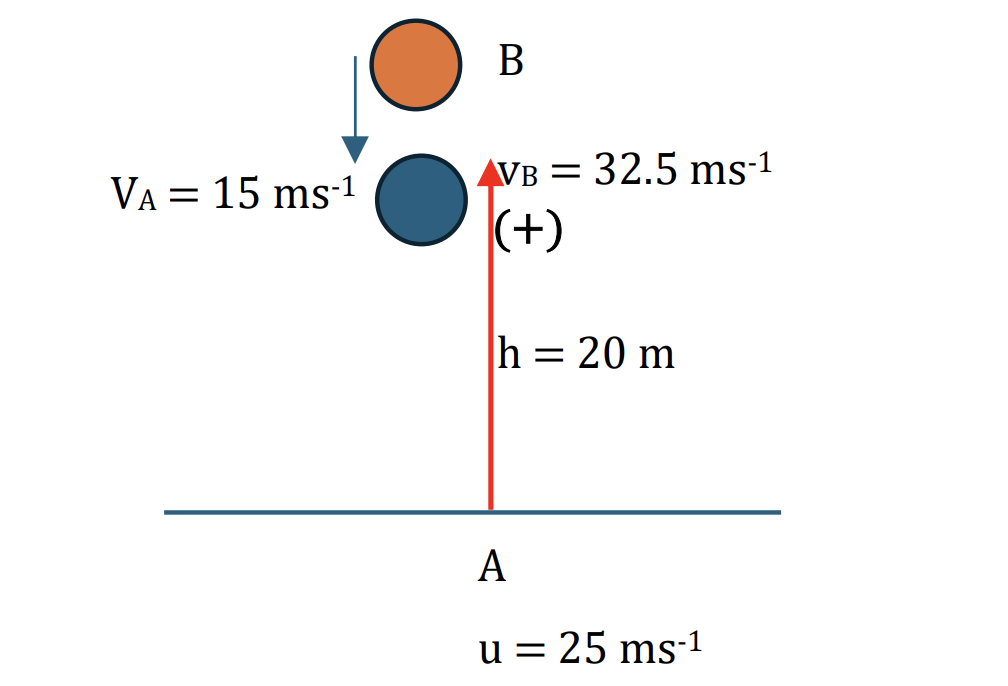
Applying the conservation of linear momentum:
Total initial momentum = Total final momentum
`m_A*vec(v_A) + m_B*vec(v_B) = m_A*vec(v_A) + m_B*vec(v_B)`
Choose positve direction is to upwards, we have:
`0.5 *15 + 0.3 * (-32.5) = 0.5 * v + 0.3 * 0`
v = `frac(0.5*15 + 0.3*(-32.5))(0.5) = -4.5 ms^-1`. So the speed of A is 4.5 ms-1 with the direction is downwards. (shown) [2]
c. Using the SUVAT equation for particle A and B
At point A, choose direction is downward
`s = ut_A + 1/2*g t_A^2`
(with a = g = 10 ms-2, same direction with g)
`20 = 4.5 * t_A + 1/2 *10 * t_A^2`
`t_A = 1.6 s or t_A = - 2.5`(cancel) [1.5]
The time interval between A and B reaching the ground:
`∆t = |t_B- t_A| = |2- 1.6| = 0.4 s [1]`
Question 1
Calculate the momentum of:
a. A tennis ball of mass 0.056kg and velocity 35 ms-1. [1]
b. A piano of mass 160kg falling with a speed of 10 ms-1. [1]
c. A lion of mass 180kg running at a speed of 30kmh-1. [1]
Question 2
Annie and her younger brother Ryan are at the ice rink. They stand facing each other, then Annie pushes against Ryan and they both move backwards. Annie estimates that her movement is 1.5 ms-1.
Given that Annie has mass 40kg and Ryan has mass 30kg, how fast is Ryan moving? [2]
Question 3
Particle P of mass m kg and Q of mass 0.2 kg are free to move on a smooth horizontal plane.
P is projected at a speed of 2 ms-1 towards Q which is stationary. After the collision P and W move in opposite direction with speed of 0.5 ms-1 and 1 ms-1 respectively.
Find m [3]
Question 4
Two particles P and Q of masses 0.2kg and 0.5kg respectively, are at rest on smooth horizontal plane. P is projected towards Q with speed 2ms-1.
a. Write down the momentum of P [1]
b. After the collision P continues to move in the same direction with speed 0.3 ms-1.
Find the speed of Q after the collision [2]
Question 5
Ryan makes a cart, which he can jump onto and move, He decides to test it on a smooth, flat road. He stands on it, but it does not move.
We He tries again, jumping from a standing position and landing on the cart with a horizontal speed of 0.5 ms-1. Ryan has a mass of 40 kg and the cart has a mass of 12 kg.
a. Calculate the speed of the cart with Ryan riding on it. [2]
He tries a running start, starting 2m away from the cart and accelerating from rest at a rate of 0.25 ms-2.
b. Calculate the new speed of cart with Ryan riding on it. [3]
He wants the cart to go at a speed of 2ms-1.
c. How far will he have to run at this same rate of acceleration, before jumping into the cart, to achieve this final speed? Is this a realistic situation? [3]
Question 6
a. A basketball weighs 13 times more than a golf ball. If they are thrown at each other with an equal and opposite velocity u, show that vg = 12u – 13vb where vg is velocity of the golf ball after impact and vb is the velocity of the basketball after impact. [2]
b. A bullet of mass m kg is fired from a gun of mass M kg, which is free to recoil. Let the initial velocities of the bullet and gun be u ms-1 and U ms-1, respectively.
Show that the initial speeds of the bullet and gun are in inverse ratio to their masses. [3]
Question 7
A bus of mass 10 tonnes is following a car of mass 1.2 tonnes at a distance of 30m. Initially, both are travelling at a constant speed of 36 kmh-1 . The driver’s foot slips and causes the bus to accelerate uniformly. After 5 seconds, the bus crashes into the back of the car, and the two vehicles coalesce.
Find the acceleration (in ms-1) of the bus and the velocity (in kmh-1) of the vehicles immediately after the crash. [5]
Question 8
A particle B of mass 5 kg is at rest on a smooth horizontal table. A particle A of mass 2.5 kg moves on the table with a speed of 6 ms-1 and collides directly with B. In the collision the two particles coalesce.
a. Find the speed of the combined particle after the collision. [2]
b. Find the loss of kinetic energy of the system due to the collision. [3]
Question 9
Two objects A and B of mass 4.5kg and m kg approach each other at speeds of 4 ms-1 and 6 ms-1, respectively. They coalesce on impact.
a. Calculate the value of m if the two objects cease to move after impact. [2]
b. Calculate the value of m if they move at 2.4 ms-1 in the direction of B after impact. [2] In fact, m = 18 kg.
c. Calculate the final velocity of the combined mass, making the direction clear. [2]
After a short time, the combined mass breaks apart into two sections with masses 10.5kg and 12 kg. The 10.5 kg section moves in the same direction as the combined mass but with a speed of 1 ms-1. [2]
Question 10
Two small smooth spheres A and B of equal radii and of masses 4 kg and m kg respectively, lie on a smooth horizontal plane. Initially, sphere B is at rest and A is moving towards B with speed 6 m s−1. After the collision A moves with the speed of 1.5 m s−1 and B moves with speed 3 m s−1.
Find the two possible values of the loss of kinetic energy due to the collision. [6]
Question 11
A railway engine of mass 25000 kg is positioned 50 m behind two carriages, each of mass 15000 kg, which are also 50m apart. The resistances to forward motion are 2kN on the engine and 0.5 kN on each of the carriages. The train is on a straight flat section of the track. The engine begins at rest and starts to produce a driving force of 18kN. As the engine meets the carriages, they instantaneously join together to form a larger train.
Calculate the ϐinal velocity of the engine after it has connected with the second carriage. [6]
Question 12
Two particles A and B have masses of 3 kg and 2 kg respectively. They are moving along a straight horizontal line towards each other. Each particle is moving with a speed of 4 ms-1 when they collide.

a. If the particles coalesce during the collision to form a single particle, find the speed of the combined particle after the collision. [2]
b. If, after the collision, A moves in the same direction as before the collision with speed 0.4 ms-1, find the speed of B after the collision. [2]
Question 13
Two particles P and Q of maqsses 0.2 kg and 0.3 kg respectively are free to move in a horizontal straight line on a smooth horizontal plane. P is projected towards Q with speed 0.5 ms-1.
At the same instant, Q is projected towards P with speed of 1ms-1. Q comes to rest in the resulting collision.
Find the speed of P after the collision. [2]
Question 14
Two particles A and B of masses 0.4 kg and 0.2 kg respectively, are moving down the same line of greatest slope of a smooth plane. The plane is inclined at 30o to the horizontal, and A is higher up the plane than B. When the particles collide, the speeds of A and B are 3 ms−1 and 2 ms−1 respectively. In the collision between the particles, the speed of A is reduced to 2.5m s−1.
a. Find the speed of B immediately after the collision. [2]
After the collision, when B has moved 1.6 m down the plane from the point of collision, it hits a barrier and returns up the same line of greatest slope. B hits the barrier 0.4 s after the collision, and when it hits the barrier, its speed is reduced by 90%. The two particles collide again 0.44 s after their previous collision, and they then coalesce on impact.
b. Show that the speed of B immediately after it hits the barrier is 0.5m s−1. Hence find the speed of the combined particle immediately after the second collision between A and B. [7]
Question 15
Two particles P and Q of masses 0.3 kg and 0.2 kg respectively, are at rest on a smooth horizontal plane. P is projected at a speed of 4 ms−1 directly towards Q. After P and Q collide, Q begins to move with a speed of 3 ms−1.
a. Find the speed of P after the collision. [2]
After the collision, Q moves directly towards a third particle R, of mass m kg, which is at rest on the plane. The two particles Q and R coalesce on impact and move with a speed of 2 ms−1.
b. Find m. [2]
Question 16
Two particles P and Q of masses m kg and 0.3 kg respectively, are at rest on a smooth horizontal plane. P is projected at a speed of 5ms−1 directly towards Q. After P and Q collide, P moves with a speed of 2 ms−1 in the same direction as it was originally moving.
a. Find, in terms of m, the speed of Q after the collision. [2]
After this collision, Q moves directly towards a third particle R, of mass 0.6 kg, which is at rest on the plane. Q is brought to rest in the collision with R, and R begins to move with a speed of 1.5 m s−1.
b. Find the value of m. [2]
Question 17
Two particles A and B of masses 3.2 kg and 2.4 kg respectively, lie on a smooth horizontal table. A moves towards B with a speed of v ms−1 and collides with B, which is moving towards A with a speed of 6 ms−1.
a. In the collision, the two particles come to rest. a. Find the value of v [2]
b. Find the loss of kinetic energy of the system due to the collision [2]
Question 18
Two particles P and Q of masses 0.1 kg and 0.4 kg respectively, are free to move on a smooth horizontal plane. Particle P is projected with speed 4ms−1 towards Q which is stationary. After P and Q collide, the speeds of P and Q are equal.
Find the two possible values of the speed of P after the collision. [3]
Question 19
Two particles P and Q of masses 6 kg and 2 kg respectively, lie at rest 12.5 m apart on a rough horizontal plane. The coefficient of friction between each particle and the plane is 0.4. Particle P is projected towards Q with speed 20 ms−1.
a. Show that the speed of P immediately before the collision with Q is `10sqrt3`ms−1. [3]
In the collision, P and Q coalesce to form particle R.
b. Find the loss of kinetic energy due to the collision. [4]
Question 20
A particle A of mass 0.5 kg is projected vertically upwards from horizontal ground with speed 25m s−1.
a. Find the speed of A when it reaches a height of 20 m above the ground. [2]
When A reaches a height of 20 m, it collides with a particle B of mass 0.3 kg which is moving downwards in the same vertical line as A with speed 32.5 ms−1. In the collision between the two particles, B is brought to instantaneous rest.
b. Show that the velocity of A immediately after the collision is 4.5ms−1 downwards. [2]
c. Find the time interval between A and B reaching the ground. You should assume that A does not bounce when it reaches the ground. [4]