Question 1
a. Find the magnitude of the resultant force acting on a particle of mass 800g that would produce an acceleration of 3.1 ms-2 [1]
b. A particle of mass m kg has a deceleration of 4 ms-2 when acted upon by a resultant force of 5.2 kN. Find the value of m [1].
Easy
Mark as Complete
Mark Scheme
Question 2
A minibus of mass 1500 kg produces a driving force of 1125N. Given that the initial velocity of the minibus is 4 ms-2, find the time it takes the minibus to travel 385m along a straight horizontal road.
The coefficient of friction between the minibus and the road is 0.035 and the gravitational acceleration is given 9.8 m.s-2 [4]
Easy
Mark as Complete
Mark Scheme
Question 3
A car of mass 960 kg accelerates from 15 ms-1 to 30 ms-1 along a straight 400 m stretch of a horizontal motorway at a constant rate. During this acceleration, the engine produces a driving force of 1.24 kN. The motorist then spots a fault on the dashboard and decides to pull over onto the har shoulder, removing the driving force. The car then decelerates at a constant rate with a braking force of 500N.
Assuming that the frictional force is constant throughout, how much further does the car travel before it comes to rest? [4]
Medium
Mark as Complete
Mark Scheme
Question 4
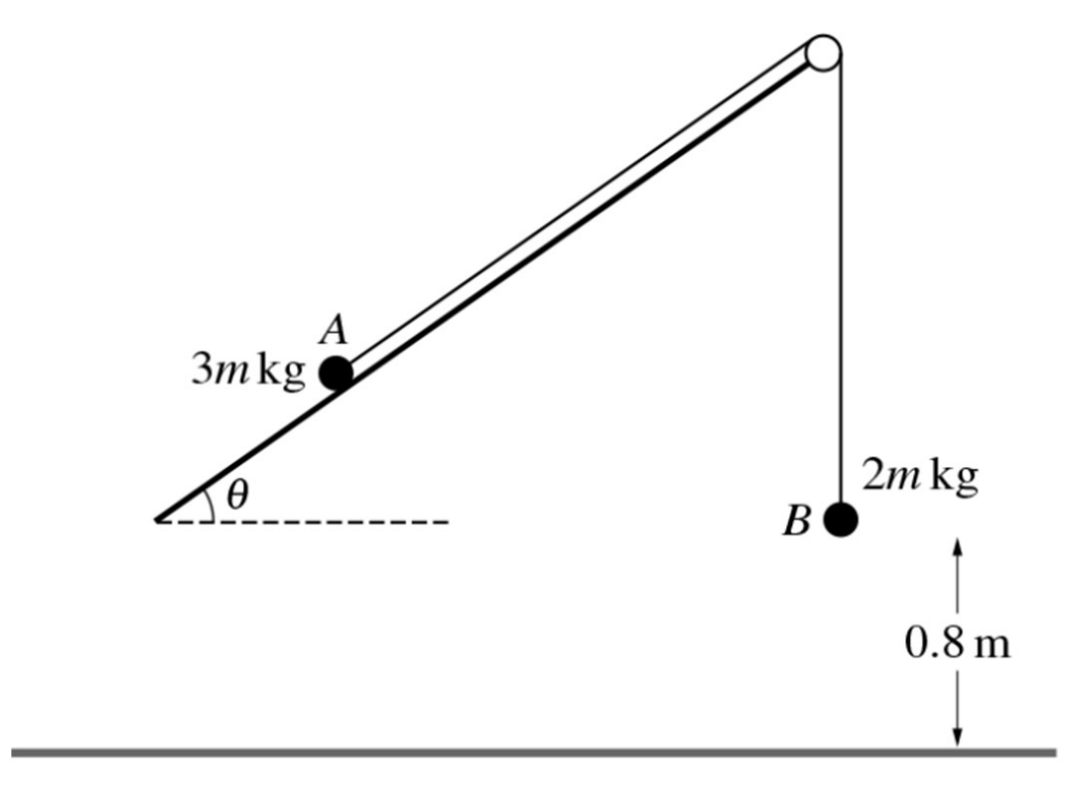
Two particles A and B, of masses 3 m kg and 2 m kg respectively, are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley which is attached to the edge of a plane. The plane is inclined at an angle `theta` to the horizontal. A lies on the plane and B hangs vertically, 0.8 m above the floor, which is horizontal. The string between A and the pulley is parallel to a line of the greatest slope of the plane. Initially, A and B are at rest. (g = 10 ms-2)
a. Given that the plane is smooth, find the value of `theta` for which A remains at rest. [3] It is given instead that the plane is rough, `theta` = 30o and the acceleration of A up the plane is 0.1 ms-2.
b. Show that the coefficient of friction between A and the plane is `1/10 sqrt3`. [5]
c. When B reaches the floor it comes to rest. Find the length of time after B reaches the floor for which A is moving up the plane. (You may assume that A does not reach the pulley) [4]
Medium
Mark as Complete
Mark Scheme
Question 5
A car of mass 1400 kg is moving along a straight horizontal road against a resistance of magnitude 350N.
a. Find, in kW, the rate at which the engine of the car is working when it is traveling at a constant speed of 20 ms-1. [2]
b. Find the acceleration of the car when its speed is 20 ms-1 and the engine is working at 15 kW. [3]
Easy
Mark as Complete
Mark Scheme
Question 6
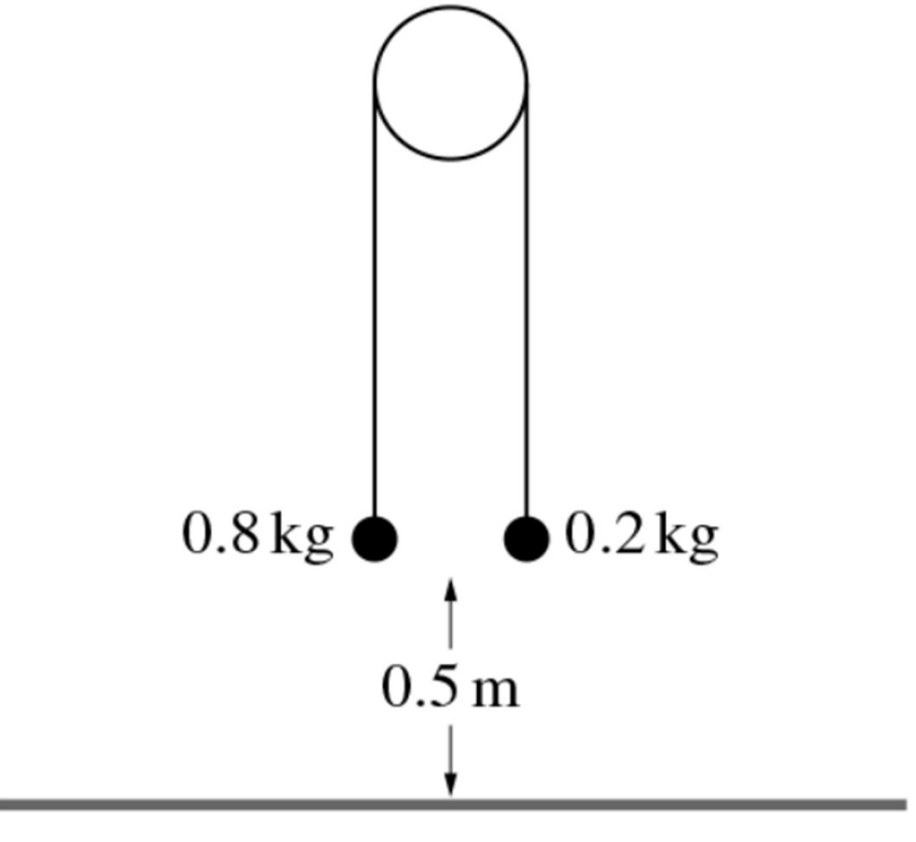
Two particles of masses 0.8 kg and 0.2 kg are connected by a light inextensible string that passes over a fixed smooth pulley. The system is released from rest with both particles 0.5 m above a horizontal floor (see diagram).
In the subsequent motion the 0.2 kg particle does not reach the pulley.
a. Show that the magnitude of the acceleration of the particles is 6 ms-2 and find the tension in the string. [4]
When the 0.8 kg particle reaches the floor it comes to rest.
b. Find the greatest height of the 0.2 kg particle above the floor. [3]
Easy
Mark as Complete
Mark Scheme
Question 7
A block of mass 5 kg is placed on a plane inclined at 30o to the horizontal. The coefficient of friction between the block and the plane is `mu`.
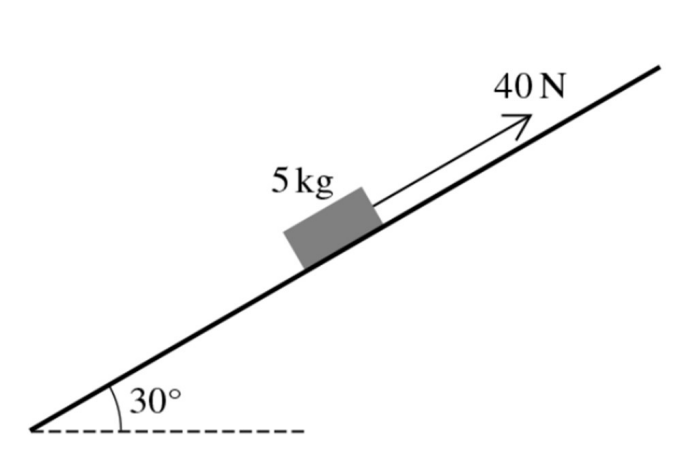
When a force of magnitude 40 N is applied to the block, acting up the plane parallel to a line of greatest slope, the block begins to slide up the plane.
Show that `mu < 1/5 sqrt3 [4]`
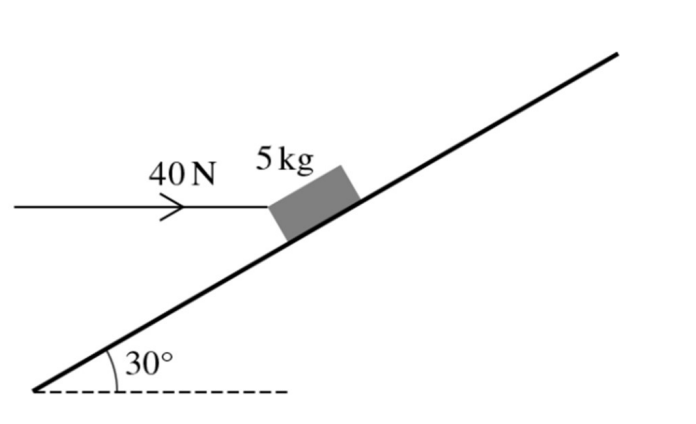
When a force of magnitude 40N is applied horizontally, in a vertical plane containing a line of greatest slope, the block does not move.
Show that, correct to 3 decimal places, the least possible value of `mu` is 0.152. [4]
Medium
Mark as Complete
Mark Scheme
Question 8
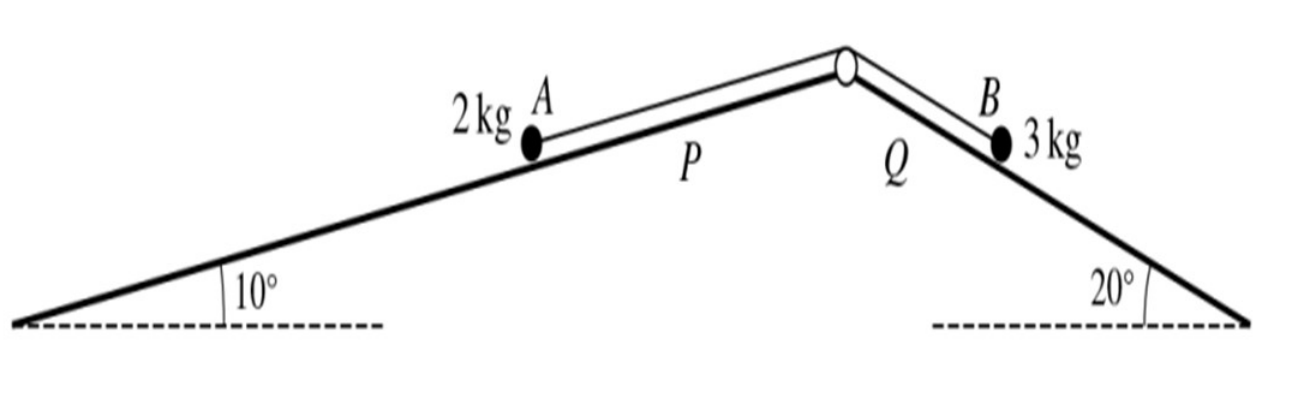
As shown in the diagram, particles A and B of masses 2 kg and 3 kg respectively are attached to the ends of a light inextensible string. The string passes over a smal ϐixed smooth pulley which is attached to the top of two inclined planes. Particle A is on plane P, which is inclined at an angle of 10o to the horizontal. Particle B is on plane Q, which is inclindes at an angle of 20o to the horizontal. The string is taut, and the two parts of the string are parallel to lines of greatest slope of their respective planes.
a. It is given that plane P is smooth, plane Q is rough, and the particles are in limiting equilibrium. Find the coefϐicient of friction between particle B and plane Q. [5]
b. It is given instead that both planes are smooth and that the particles are released from rest at the same horizontal level. [6]
Hard
Mark as Complete
Mark Scheme
Question 9
A constant resistance to motion of magnitude 350 N acts on a car of mass 1250 kg. The engine of the car exerts a constant driving force of 1200 N. The car travels a long a road inclined at an angle of ? to the horizontal, where sin`theta` = 0.05.
Find the speed of the car when it has moved 100m from rest in each of the following cases.
Easy
Mark as Complete
Mark Scheme
Question 10
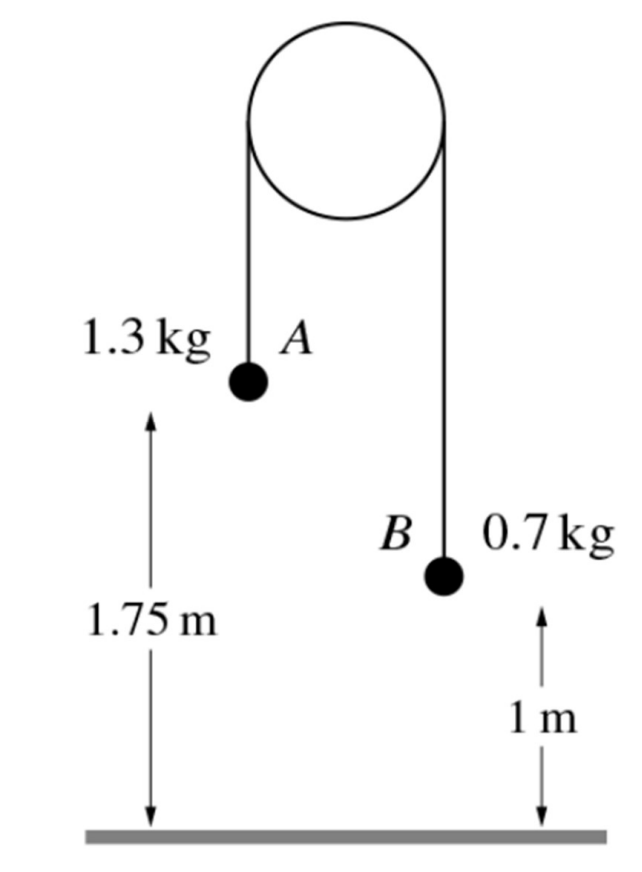
Two particles A and B of masses 1.3 kg and 0.7 kg respectively, are connected by a light inextensible string which passes over smooth fixed pulley. Particle A is 1.75 m above the ϐloor and particle B is 1m above the floor.
The system is released from rest with the string taut, and the particle moves vertically. When the particles are at the same height the string breaks.
Hard
Mark as Complete
Mark Scheme
Question 11
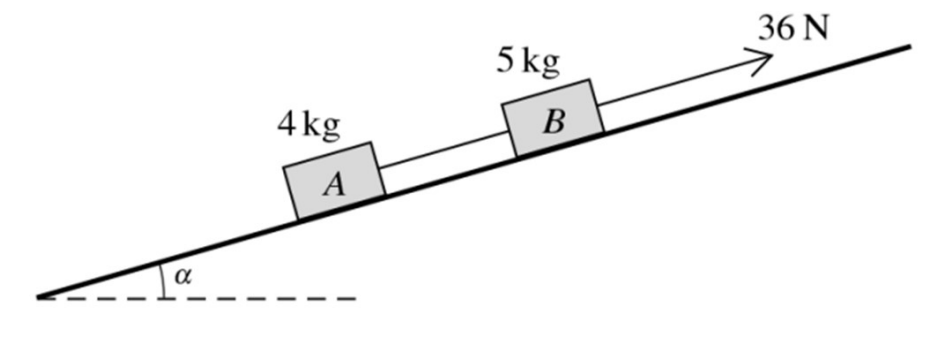
Two blocks A and B of masses 4 kg and 5 kg respectively are joined by a light inextensible string. The blocks rest on a smooth plane inclined at an angle ? to the horizontal, where tan ? = `7/24`. The string is parallel to the line of greatest slope of the plane with B above A. A force of magnitude 36N acts on B, parallel to a line of greatest slope of the plane.
a. Find the acceleration of the blocks and tension in the string. [5]
b. At a particular instant, the speed of the blocks is 1ms-1. Find the time, after this instant, that it takes for the blocks to travel 0.65 m. [2]
Medium
Mark as Complete
Mark Scheme
Question 12
A particle of mass 0.4 kg is released from rest at a height of 1.8 m above the surface of the water in a tank. There is no instantaneous change of speed when the particle enters the water. The water exerts an upward force of 5.6N on the particle when it is in the water.
a. Find the velocity of the particle at the instant when it reaches the surface of the water. [2]
b. Find the time that it takes from the instant when the particle enters the water until it comes to instantaneous rest in the water. You may assume that the tank is deep enough so that the praticle does not reach the bottom of the tank. [4]
c. Sketch a velocity-time graph for the motion of the particle from the instant at which it is released until it comes to instantaneous rest in the water. [3]
Medium
Mark as Complete
Mark Scheme
Question 13
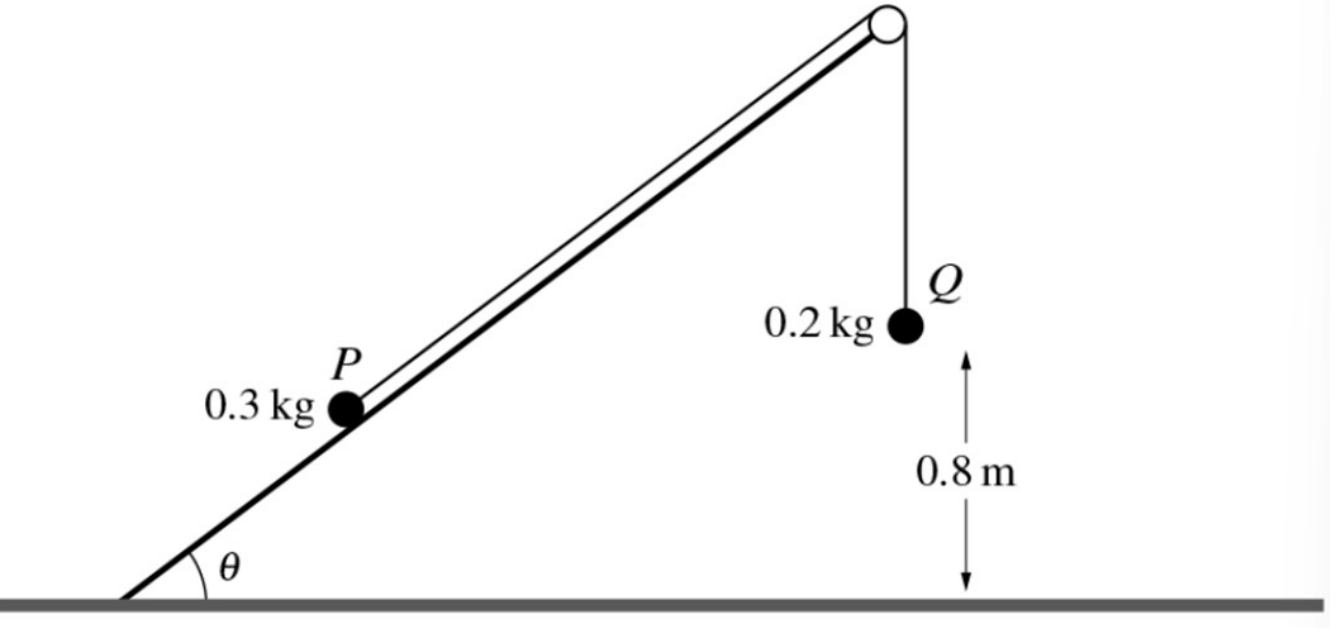
Two particles P and W of masses 0.3 kg and 0.2 kg respectively, are attached to the ends of light inextensible string. The string passes over a ϐixed smooth pulley which is attached to the edge of a smooth plane. The plane is inclined at an angle `theta` to the horizontal, where sin`theta = 3/5` . P lies on the plane and Q hangs vertically below the pulley at a height of 0.8 m above the floor. The string between P and the pulley is parallel to a line of greatest slope of the plane. P is released from rest and Q moves vertically downwards.
a. Find the tension in the string and the magnitude of the acceleration of the particles. [5]
Q hits the floor and does not bounce. It is given that P does not reach the pulley in the subsequent motion.
b. Find the time, from the instant at which P is released, for Q to reach the floor. [2]
c. When Q hits the floor, the string becomes slack. Find the time, from the instant at which P is released, for the string to become taut again. [4]
Medium
Mark as Complete
Mark Scheme
Question 14
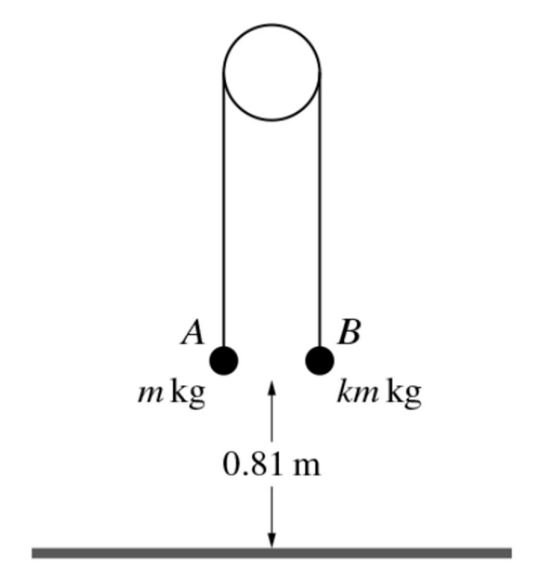
Two particles A and B have masses m kg and km kg respectively, where k >1. The particles are attached to the ends of a light inextensible string. The string passes over a ϐixed smooth pulley and the partices hang vertically below it. Both particles are at a height of 0.81 m above horizontal ground. The system is released from rest and particle B reaches the ground 0.9 s later. Particle A does not reach the pulley in its subsequent motion.
a. Find the value of k and show that the tension in the string before B reaches the ground is equal to 12m N. [7]
At the instant when B reaches the ground, the string breaks.
b. Show that the speed of A when it reaches the ground is 5.97 ms-1, correct to 3 s.f, and find the time taken, after the string breaks, for A to reach the ground. [4]
Medium
Mark as Complete
Mark Scheme
Question 15
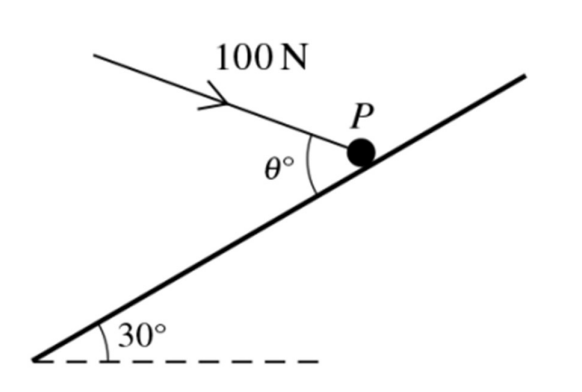
A particle P of mass 8 kg is on a smooth plane inclined at an angle of 30o to the horizontal. A force of magnitude 100N, making an angle of `theta^o` with a line of greatest slope and lying in the vertical plane containing the line of greatest slope, acts on P.
a. Given that P is in equilibrium, show that `theta` = 66.4, correct to 1 decimal place, and find the normal reaction between the plane and P. [4]
b. Given instead that `theta` = 30, find the acceleration of P. [2]
Easy
Mark as Complete
Mark Scheme
Question 16
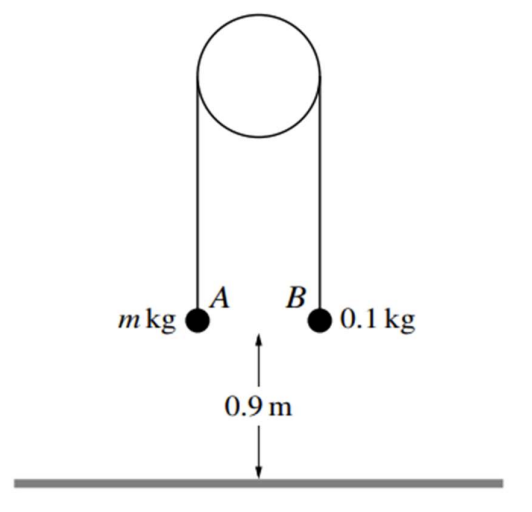
Two particles A and B have masses m kg and 0.1 kg respectively, where m > 0.1.
The particles are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley and the particles hang vertically below it. Both particles are at a height of 0.9 m above horizontal ground (see diagram).
The system is released from rest, and while both particles are in motion the tension in the string is 1.5 N. Particle B does not reach the pulley.
a. Find m. [4]
b. Find the speed at which A reaches the ground. [2]
Easy
Mark as Complete
Mark Scheme
Question 17
A ring of mass 0.3 kg is threaded on a horizontal rough rod. The coefϐicient of friction between the ring and the rod is 0.8. A force of magnitude 8 N acts on the ring. This force acts at an angle of 100 above the horizontal in the vertical plane containing the rod.
Find the time taken for the ring to move, from rest, 0.6 m along the rod. [6]
Medium
Mark as Complete
Mark Scheme
Question 18
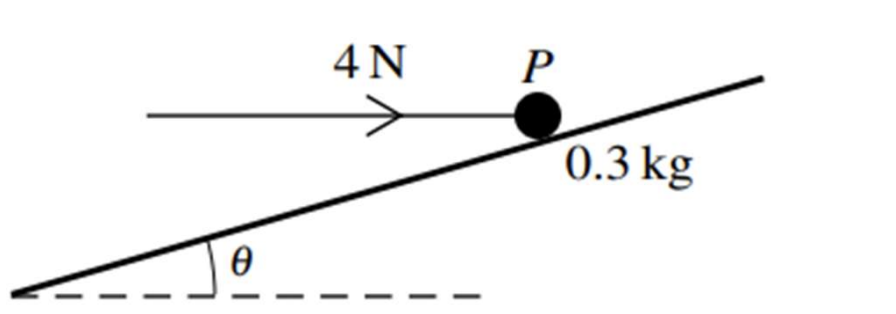
A particle P of mass 0.3 kg rests on a rough plane inclined at an angle 1 to the horizontal, where `sintheta = 7/25` . A horizontal force of magnitude 4 N, acting in the vertical plane containing a line of greatest slope of the plane, is applied to P (see diagram). The particle is on the point of sliding up the plane.
a. Show that the coefficient of friction between the particle and the plane is `3/4` . [4]
The force acting horizontally is replaced by a force of magnitude 4 N acting up the plane parallel to a line of greatest slope.
b. Find the acceleration of P [3]
c. Starting with P at rest, the force of 4 N parallel to the plane acts for 3 seconds and is then removed. Find the total distance travelled until P comes to instantaneous rest. [3]
Medium
Mark as Complete
Mark Scheme
Question 19
Two particles A and B of masses 2.4 kg and 1.2 kg respectively, are connected by a light inextensible string which passes over a fixed smooth pulley. A is held at a distance of 2.1 m above a horizontal plane and B is 1.5 m above the plane. The particles hang vertically and are released from rest. In the subsequent motion A reaches the plane and does not rebound and B does not reach the pulley.
a. Show that the tension in the string before A reaches the plane is 16 N and find the magnitude of the acceleration of the particles before A reaches the plane. [4]
b. Find the greatest height of B above the plane. [3]
Easy
Mark as Complete
Mark Scheme
Question 20
Two particles P and Q of masses 0.5 kg and 0.3 kg respectively, are connected by a light inextensible string. The string is taut, and P is vertically above Q. A force of magnitude 10 N is applied to P vertically upwards. Find the acceleration of the particles and the tension in the string connecting them. [5]
Easy
Mark as Complete
Mark Scheme
Question 1
a. Find the magnitude of the resultant force acting on a particle of mass 800g that would produce an acceleration of 3.1 ms-2 [1]
b. A particle of mass m kg has a deceleration of 4 ms-2 when acted upon by a resultant force of 5.2 kN. Find the value of m [1].
a. F = ma
`to F = 0.8 * 3.1 = 2.48 ms^(-2) [1]`
b. F = ma
`to m = F/a = (5.2*10^3)/4 = 1300 kg`
Question 2
A minibus of mass 1500 kg produces a driving force of 1125N. Given that the initial velocity of the minibus is 4 ms-2, find the time it takes the minibus to travel 385m along a straight horizontal road.
The coefficient of friction between the minibus and the road is 0.035 and the gravitational acceleration is given 9.8 m.s-2 [4]
Summary:
`u = 4 ms^(-1); F = 1125N, m = 1500 kg; s= 385 m; mu = 0.035`
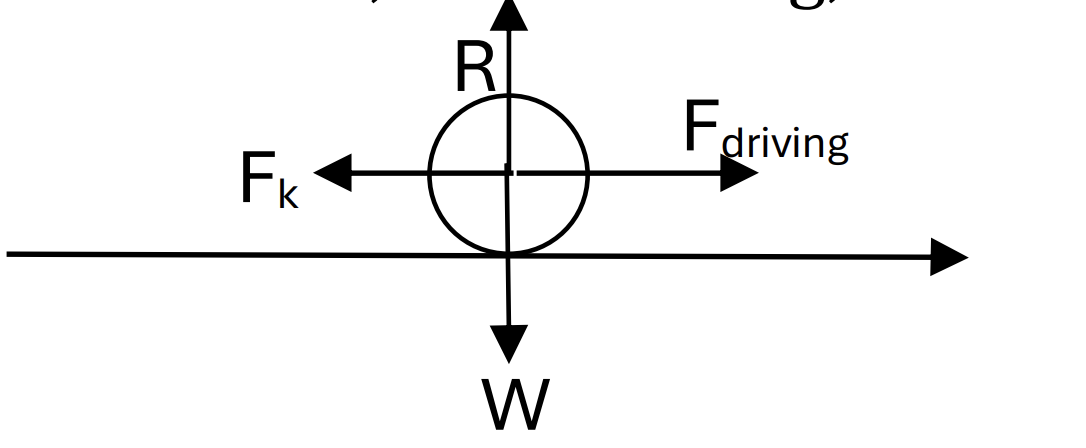
Applying the Newton’s Second Law, we have:
`vec(F_(n et) ) = vec(F_k) + vec(F_(drivi ng)` (choose direction moves to right)
`F_(n et) = - F_k + F_(drivi ng`
`ma = -muR + 1125`(Therefore R = mg) [1]
`1500 x a = -0.035 * 1500 * 9.8 +1125`
a = `610.5/1500 = 0.407 ms^(-2)` [1]`
Using SUVAT equation, we have:
`v^2 – u^2 = 2as`
`v = sqrt(4^2 + 2 * 0.407 * 385 = 18.15 ms^(-1)) [1]`
v = u + at
t = `(v- u)/a = frac(18.15 -4)(0.407) = 34.8 s [1]`
Question 3
A car of mass 960 kg accelerates from 15 ms-1 to 30 ms-1 along a straight 400 m stretch of a horizontal motorway at a constant rate. During this acceleration, the engine produces a driving force of 1.24 kN. The motorist then spots a fault on the dashboard and decides to pull over onto the har shoulder, removing the driving force. The car then decelerates at a constant rate with a braking force of 500N.
Assuming that the frictional force is constant throughout, how much further does the car travel before it comes to rest? [4]
Summary:
`m = 960 kg; u = 15 ms^(-1); v= 30 ms^(-1); s = 400m; F_(drivi ng) = 1240 N;`
`F_(braki ng) = 500N`
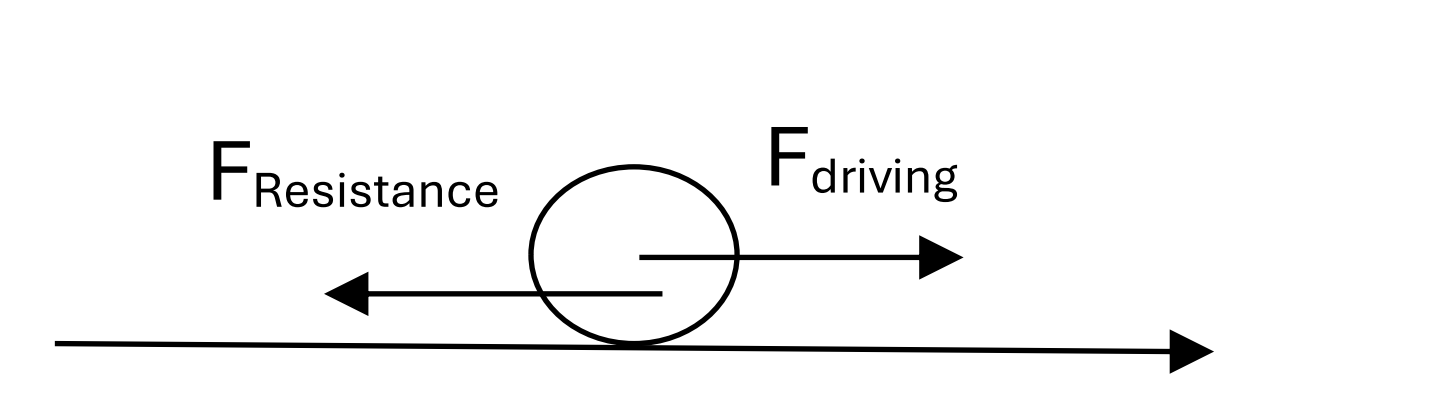
Applying the SUVAT equation, we have:
`v^2 – u^2 = 2as`
a = `(v^2 - u^2)/(2*s) = frac(30^2 - 15^2)(2*400) = 0.844 ms^(-2) [1]`
At the beginning, the resultance force is:
`F_(n et) = F_(drivi ng) - F_(resistance)` (choose direction moves to right)
`960 * 0.844 = 1240 – X`
`X = 430 N [1]`
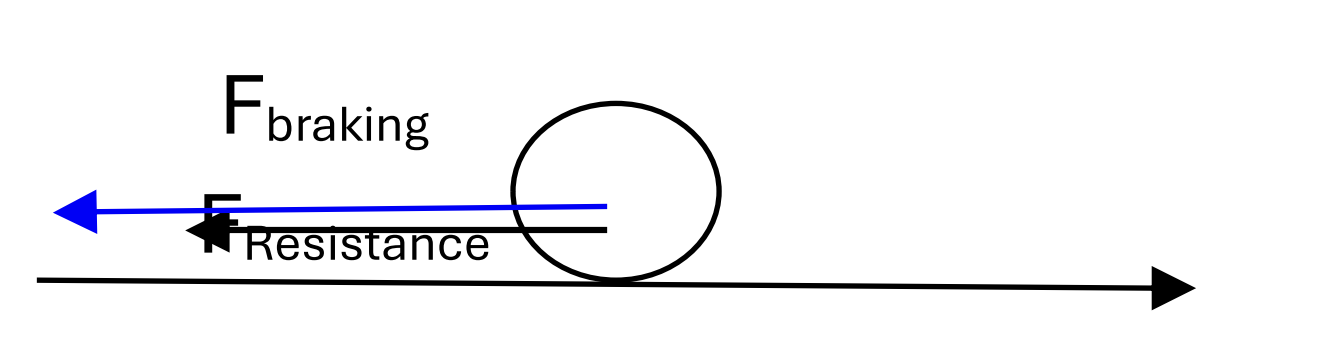
After removing the driving force, the car decelerates with a braking force, so the resultant force is:
Fnet = - (Fbraking + Fresistance)
ma = - (500 + 430) (That the resistance force is constant)
a = `frac(-(500+430))(960) = - 0.969 ms^(-2) [1]`
`v^2 – u^2 = 2as`
s = `frac(v^2 - u^2)(a *2) = frac(0^2 - 30^2)(2*-0.969) = 464 m [1]`
Question 4

Two particles A and B, of masses 3 m kg and 2 m kg respectively, are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley which is attached to the edge of a plane. The plane is inclined at an angle `theta` to the horizontal. A lies on the plane and B hangs vertically, 0.8 m above the floor, which is horizontal. The string between A and the pulley is parallel to a line of the greatest slope of the plane. Initially, A and B are at rest. (g = 10 ms-2)
a. Given that the plane is smooth, find the value of `theta` for which A remains at rest. [3] It is given instead that the plane is rough, `theta` = 30o and the acceleration of A up the plane is 0.1 ms-2.
b. Show that the coefficient of friction between A and the plane is `1/10 sqrt3`. [5]
c. When B reaches the floor it comes to rest. Find the length of time after B reaches the floor for which A is moving up the plane. (You may assume that A does not reach the pulley) [4]
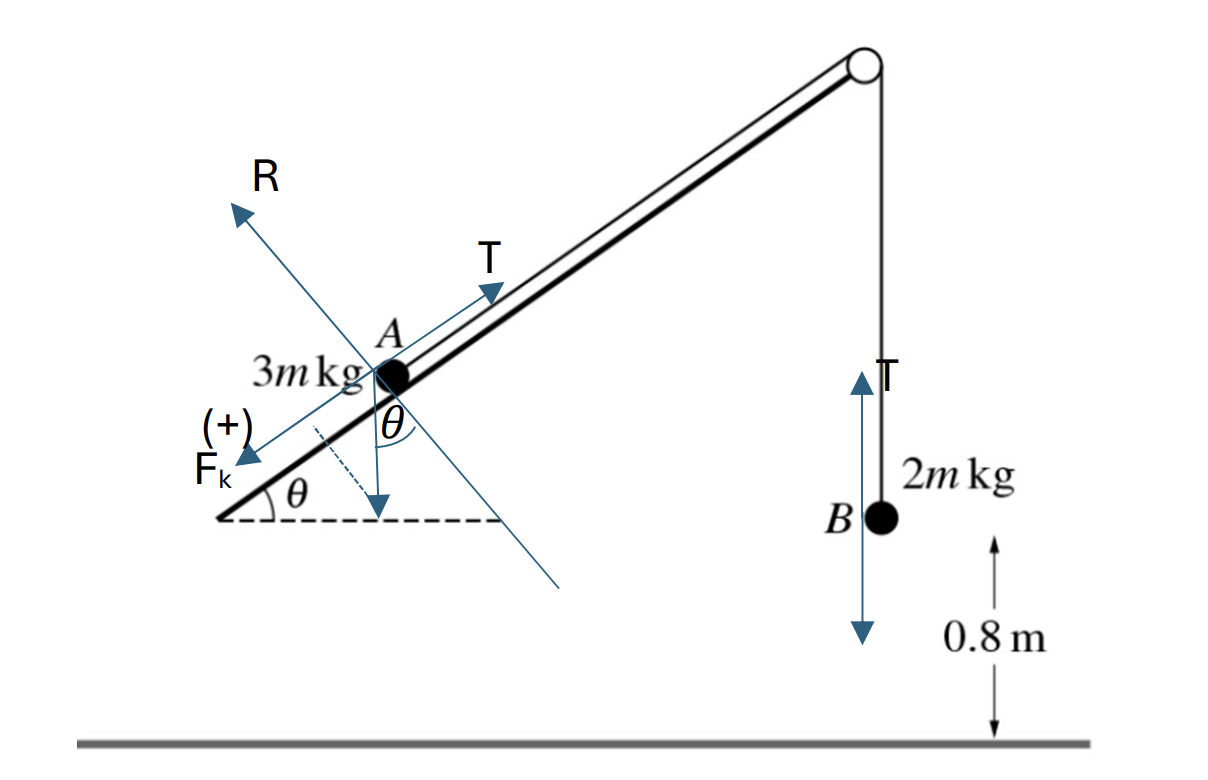
a. At point B, the particle is at rest, so the forces are in equilibrium
W = T
mB x g = T
`to 2m * 10 = T [1]`
A and B are hung in the same inextensible string, so TA = TB
At point A, the particle is at rest, the forces are in equilibrium.
`m_A * sintheta * g – T = 0`
`to 3m * sintheta * 10 – 20m = 0 [1]`
`sintheta = (20m)/(3m*10) = 2/3`
`theta = sin^-1(2/3) = 41.8^o [1]`
b. We have forces are equilibrium at point A and the acceleration of A is upwards, so choose direction is moved up.
`-F_k - m_A * sintheta * g + T = F_(n et) [1]`
`to −mu * R - m_A * sintheta * g + T = m_A * a (R = m_A * g * costheta) [1]`
`−mu * m_A * g * costheta - m_A * sintheta * g + T = m_A * a (1)`
At point B, we calculate T which has acceleration. So the forces equilibrium become:
`m_B * g – T = m_B * a`
so T = 20m – 0.2m (2) [1]
Substitute (2) into (1), we have:
`−mu * 30*m*cos30 – 30m*sin30 + 20m – 0.2m = 0.3m [1]`
`mu = frac(0.3 m + 0.2 m - 20m + 30msin30)(-30mcos30) = sqrt3/10`
c. Using SUVAT equation, we have:
`v^2 = 0 + 2 * 0.1 * 0.8` = 0.4 ms-1 [1]
A is moving up to the plane, so:
`-3mgsin30 - mu*3mgcos30 = 3ma [1]`
a = `frac(-30msin30 - sqrt3/10*30mcos30)(3m) = -6.5 ms^-2 [1]`
0 = -0.4 - 6.5 t
t = `0.4/6.5 = 0.0615 s [1]`
Question 5
A car of mass 1400 kg is moving along a straight horizontal road against a resistance of magnitude 350N.
a. Find, in kW, the rate at which the engine of the car is working when it is traveling at a constant speed of 20 ms-1. [2]
b. Find the acceleration of the car when its speed is 20 ms-1 and the engine is working at 15 kW. [3]
a. Power as rate of energy transfer P = F.v [1]
P = 350 x 20 = 7000 W = 7 kW. [1]
b. P = F.v
`F = P/v = 15000/20 = 750 N [1]`
Using Newton’s 2nd law, we have: 750 – 350 = 1400 x a [1]
`a = 400/1400 = 2/7 = 0.286 ms^-2 [1]`
Question 6

Two particles of masses 0.8 kg and 0.2 kg are connected by a light inextensible string that passes over a fixed smooth pulley. The system is released from rest with both particles 0.5 m above a horizontal floor (see diagram).
In the subsequent motion the 0.2 kg particle does not reach the pulley.
a. Show that the magnitude of the acceleration of the particles is 6 ms-2 and find the tension in the string. [4]
When the 0.8 kg particle reaches the floor it comes to rest.
b. Find the greatest height of the 0.2 kg particle above the floor. [3]
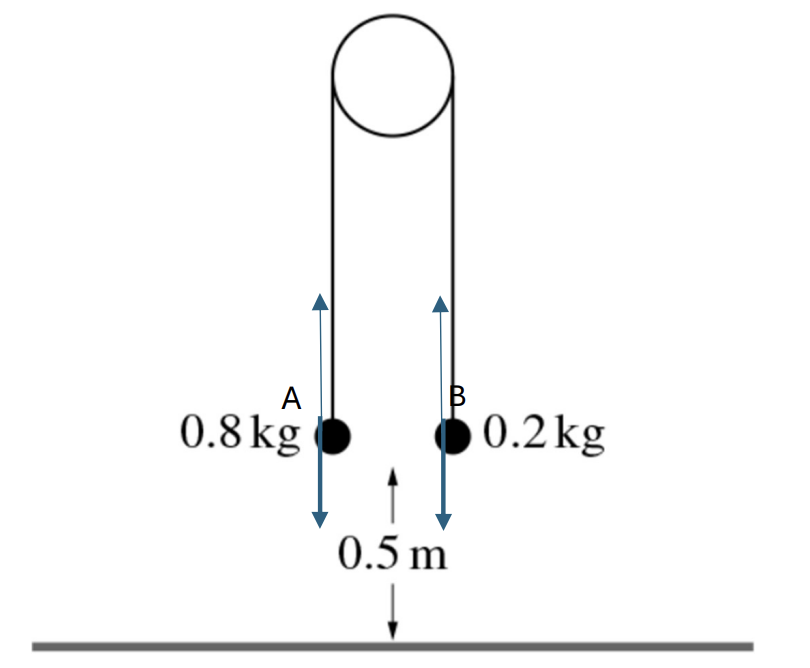
a. For particles A and B, apply the Newton’s 2nd law and choose direction moves up:
`A: 0.8 * g – T = 0.8 * a (1) [1]`
`B: T – 0.2 * g = 0.2 * a [1]`
`0.8 * g – 0.2 * g = (0.8 + 0.2) a`
`a = 6 ms^(-2) [1]`
Substitute a = 6 ms-2 in (1), so T = 3.2 N [1]
b. Particle A is moved down to the ϐloor, it also means that particle A is moved up to the same height, so sA = sB = 0.5 m. Applying the SUVAT equation, we have:
At point A: `v^2 = 2 * 6 * 0.5`
v = `sqrt(2 * 6 * 0.5) = 2.45 m/s [1]`
We find the extra height reached by particle B if the gravitational strength affects on B.
`v^2 – u^2 = 2as`
s = `frac(v^2 - u^2)(2a) = frac(2.45^2 - 0^2)(2*10) = 0.3 m [1]`
The greatest height of the particle B is 1.3 m [1]
Question 7
A block of mass 5 kg is placed on a plane inclined at 30o to the horizontal. The coefficient of friction between the block and the plane is `mu`.

When a force of magnitude 40 N is applied to the block, acting up the plane parallel to a line of greatest slope, the block begins to slide up the plane.
Show that `mu < 1/5 sqrt3 [4]`

When a force of magnitude 40N is applied horizontally, in a vertical plane containing a line of greatest slope, the block does not move.
Show that, correct to 3 decimal places, the least possible value of `mu` is 0.152. [4]
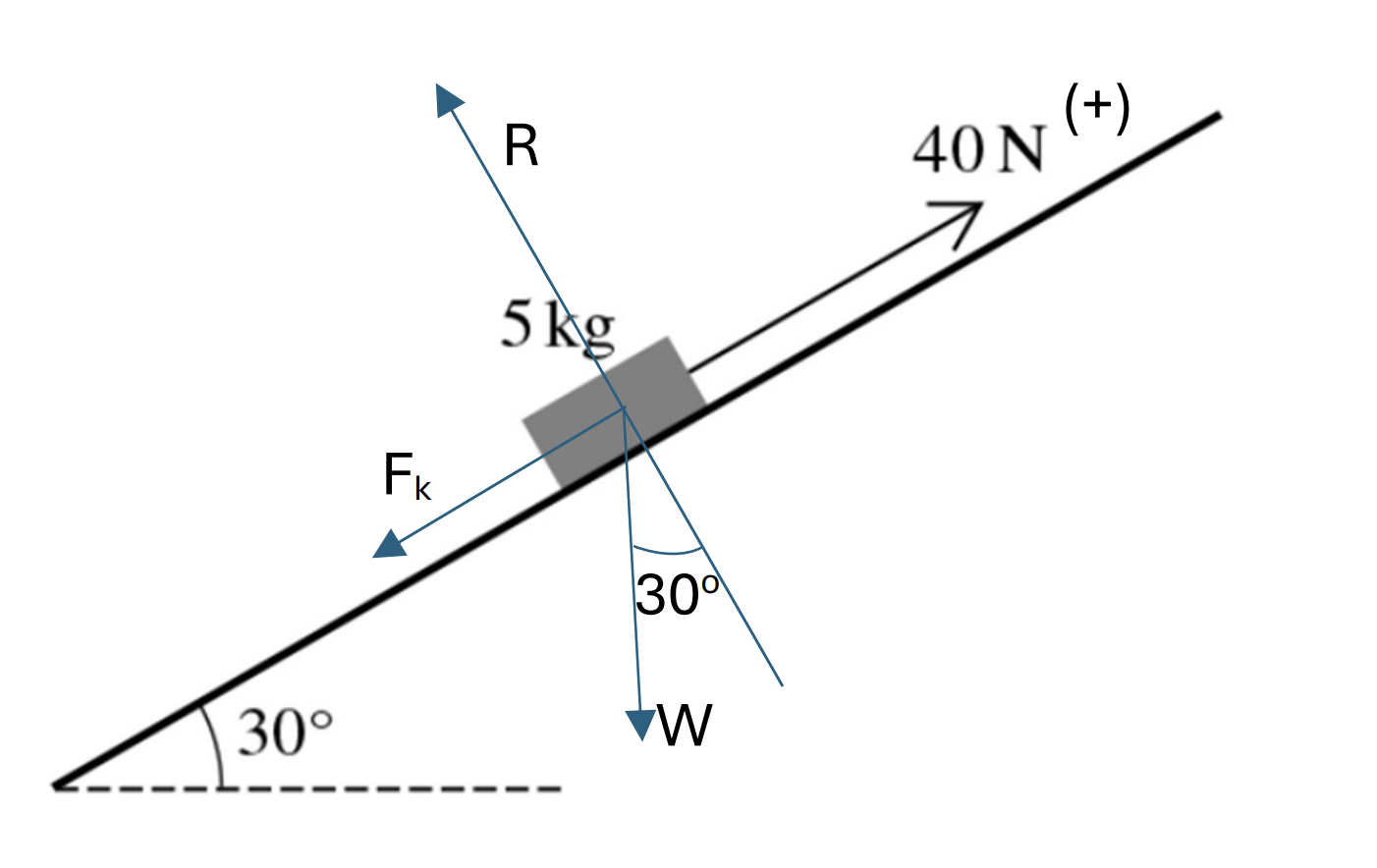
a. Assume that all the forces are equilibrium and choose the direction is to the right, we have:
`- muR – 5g*sin30 + 40 = 0` (with R = 5gcos30) [1]
`40 = mu*5g*cos30 + 5g*sin30` (g = 10 ms-2)
`mu = frac(40 - 5*10*sin30)(5 * 10 * cos 30) = sqrt3/5 [1]`
Because the block is sliding up the plane, so `mu` needs to be smaller than `sqrt3/5`. So `mu < sqrt3/5 [2]`
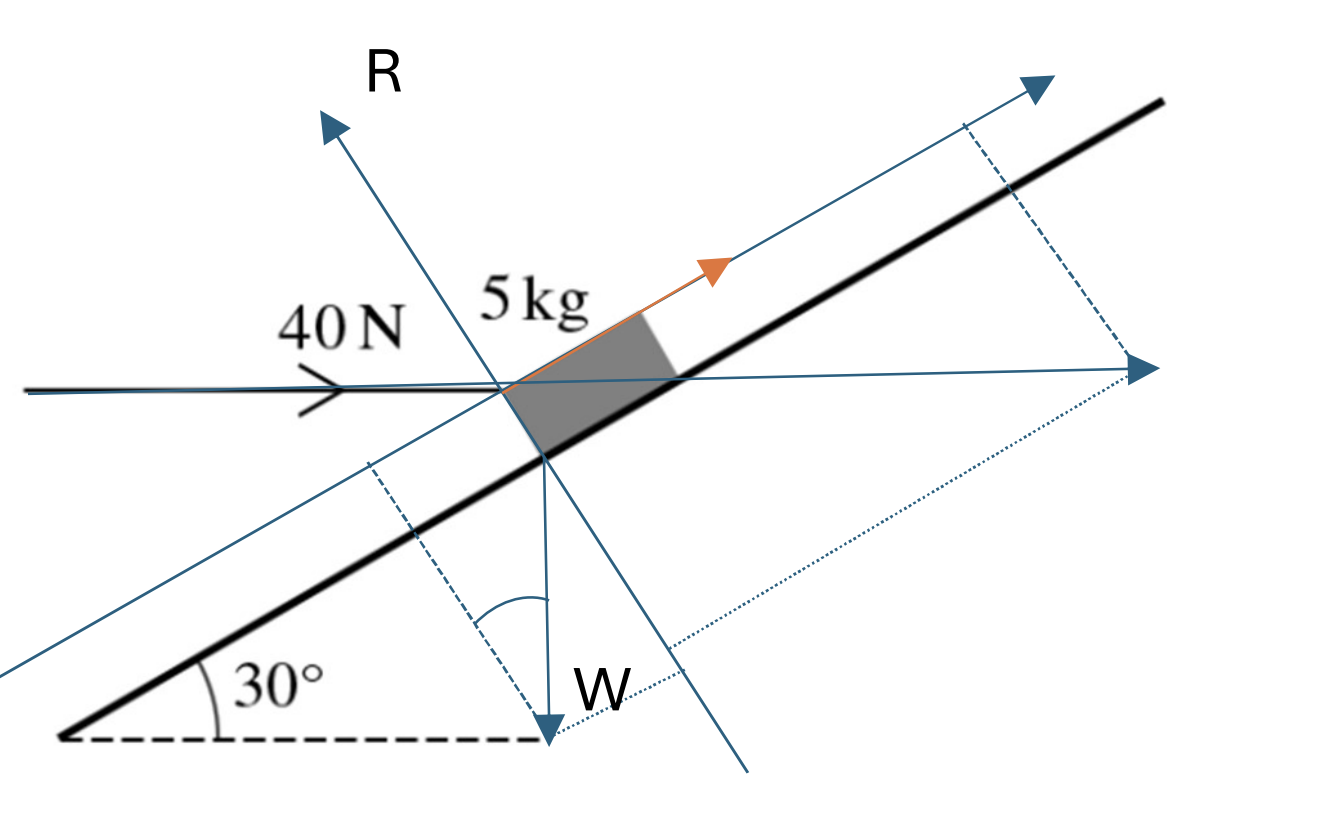
b. Assume that all the forces are equilibrium and choose the direction is to the right of the horizontal axis:
`40*cos30 – 5g*sin30 + mu R= 0 (1) [1]`
Assume that all the forces are equilibrium and choose the direction moved up of the vertical axis:
`R - 40*sin30 – 5g*cos30 = 0 (g = 10 ms^(-2))`
`R = 50 cos30 + 40sin30 (2) [1]`
Substitute (2) in (1):
`40*cos30 – 50*sin30 + mu(50 cos30 +40sin30) = 0`
`mu = frac(40cos30 - 50sin30)(50cos30 - 40sin30) = 0.152 [1]`
We have `F ≤ muR`
So `mu ≥ 0.152 [1]`
Question 8

As shown in the diagram, particles A and B of masses 2 kg and 3 kg respectively are attached to the ends of a light inextensible string. The string passes over a smal ϐixed smooth pulley which is attached to the top of two inclined planes. Particle A is on plane P, which is inclined at an angle of 10o to the horizontal. Particle B is on plane Q, which is inclindes at an angle of 20o to the horizontal. The string is taut, and the two parts of the string are parallel to lines of greatest slope of their respective planes.
a. It is given that plane P is smooth, plane Q is rough, and the particles are in limiting equilibrium. Find the coefϐicient of friction between particle B and plane Q. [5]
b. It is given instead that both planes are smooth and that the particles are released from rest at the same horizontal level. [6]
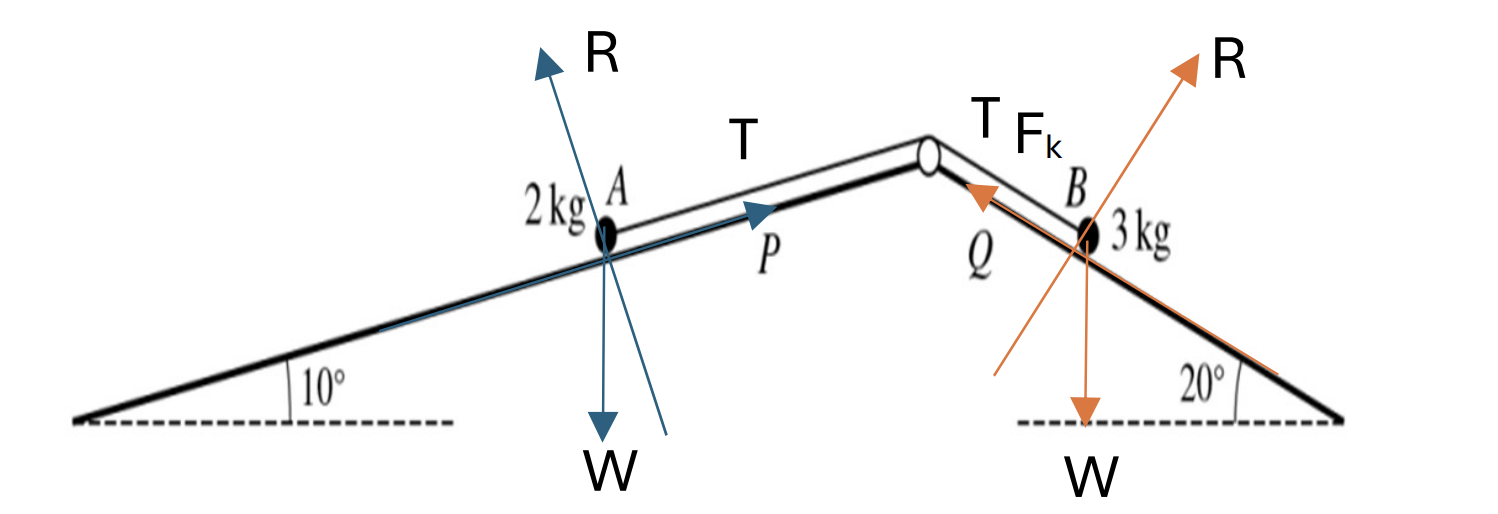
a. At point A:
`T = W_A*sin10 (with W_A = 2 * 10) [1]`
At point B:
`W_B*sin20 = T + F_k`(with WB = `3*10` and F, T are same direction) [1]
`30*sin20 = 20*sin10 + muR (R = 30*cos20) [1]`
`to 30*sin20 = 20*sin10 + mu*30*cos20 [1]`
`mu = frac(30sin20 - 20sin10)(30cos20) = 0.241 [1]`
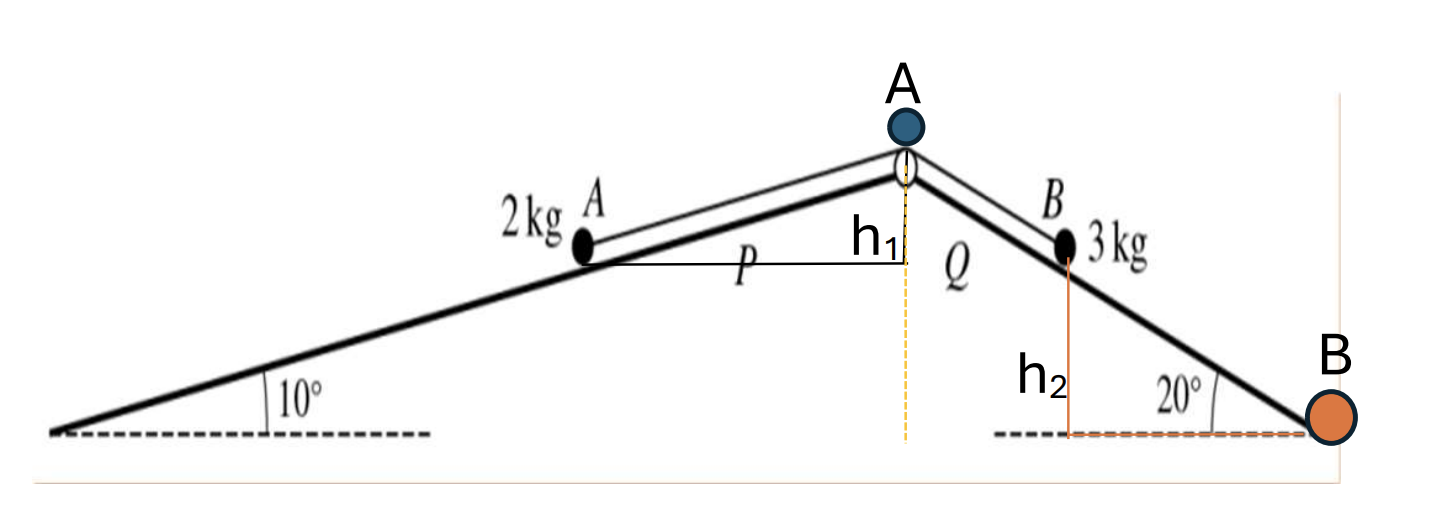
At point A:
`T – 2*g*sin10 = 2a (1) [1]`
At point B:
`3*g*sin20 – T = 3a (2) [1]`
Take (2) + (1), we have:
`30*sin20 – 20*sin10 = 5a`
a = `frac(30sin20 -20sin10)(5) = 1.36 ms^-2 [1]`
`h_1 = x sin20`
`h_2 = x sin10`
xsin20 + xsin10 = 1 [1]
x = `x = 1/(sin20 + sin10) = 1 [1]`
Applying the SUVAT equation, we have x is distance that particle A or B moved.
`x = ut + 1/2 at^2 (u = 0 ms^-2) [1]`
`1/(sin20 + sin10) = 0 + 1/2*1.36*t^2`
t = 1.69 s [1]
Question 9
A constant resistance to motion of magnitude 350 N acts on a car of mass 1250 kg. The engine of the car exerts a constant driving force of 1200 N. The car travels a long a road inclined at an angle of ? to the horizontal, where sin`theta` = 0.05.
Find the speed of the car when it has moved 100m from rest in each of the following cases.
a. When the car is moving up the hill
`v =? ms ^-1; s = 100m; u = 0 ms^ -1; a =? ms^-2; m = 1250kg; sintheta = 0.05`
Applying the Newton’s Second Law, we have
`vec(F_(n et)) = vec(F_(exert) )+ vec(F_k) + vec(W)`(choose direction is moved to right)
`F_(n et) = F_(exert) – F_k – mgsintheta [1]`
`250a = 1200 – 350 – 12500 * 0.05`
Using SUVAT equation, we have:
`v^2 – u^2 = 2as`
`v = sqrt(0^2 + 2 *0.18*100) = 6 ms^-1 [1]`
b. The car is moving down to the hill
`v =? ms ^-1; s = 100m; u = 0 ms^ -1; a =? ms^-2; m = 1250kg; sin theta = 0.05`
Applying the Newton’s Second Law, we have
`vec(F_(n et)) = vec(F_(exert)) + vec(F_k) + vec(W)` (choose direction is moved to right)
`F_(n et) = F_(exert) – F_k + mgsintheta [1]`
`1250*a = 1200 – 350 + 12500 * 0.05`
a = `frac(1200 -350 +12500*0.05)(1250)= 1.18 ms^-2 [1]`
Using SUVAT equation, we have:
`v^2 – u^2 = 2as`
`v = sqrt(0^2 + 2 * 1.18 * 100 )= 15.4 ms^-1 [1]`
Question 10

Two particles A and B of masses 1.3 kg and 0.7 kg respectively, are connected by a light inextensible string which passes over smooth fixed pulley. Particle A is 1.75 m above the ϐloor and particle B is 1m above the floor.
The system is released from rest with the string taut, and the particle moves vertically. When the particles are at the same height the string breaks.
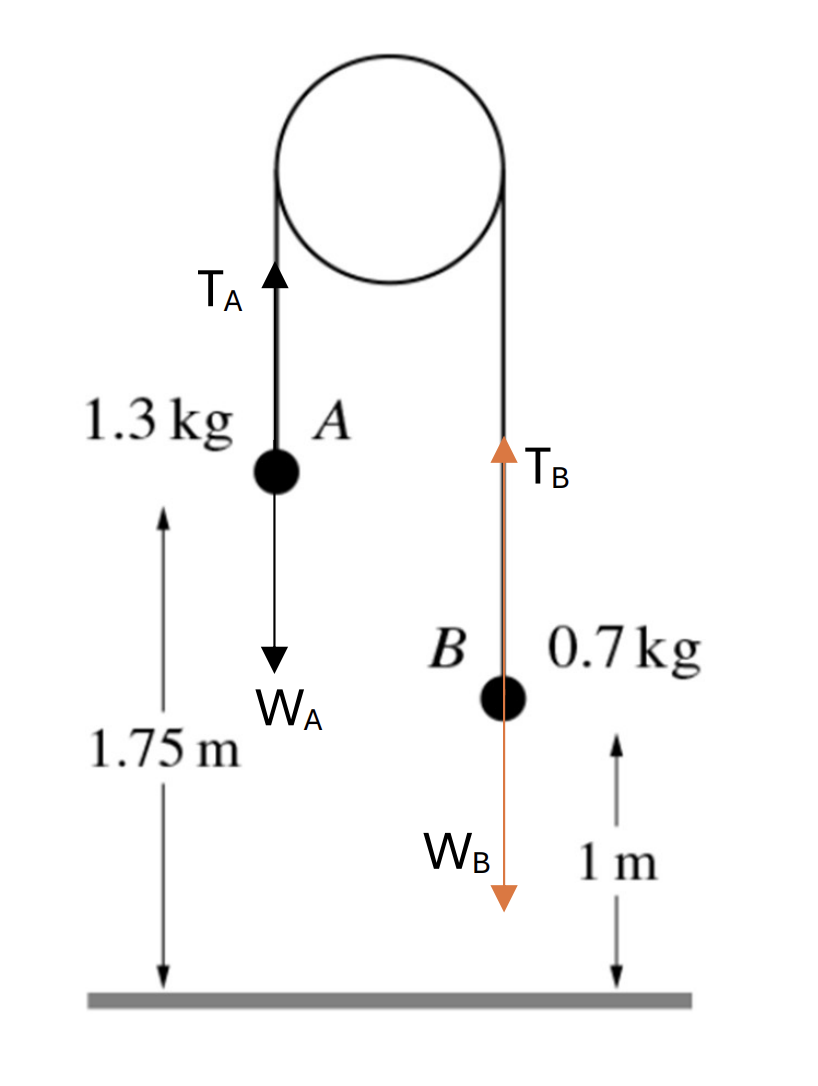
a. At point A:
`F_(n et) = vec(T_A) + vec(W_A) (choose direction of movement is moving down)`
Fnet = - TA + WA
`ma = - T_A – mg`
`1.3*a = - T_A + 1.3 * 10 (1) [1]`
At point B:
`F_(n et) = vec(T_B) + vec(W_B)` (choose direction of movement is moving up)
Fnet = TB -WB
ma = TB - mg
`0.7*a = T_B – 0.7 * 10 (2) [1]`
As the string breaks, the tension at A or B is the same, so takes (1) plus (2), we have:
`1.3*a + 0.7*a = 13 - 7`
2a = 6
`a = 3 ms^-2 [1]`
(If you calculate a is negative, it means that a has the opposite direction from the direction you chose)
The tension is `1.3 * 3 = - T_A + 13 or 0.7 * 3 = T_B – 7`
`T_A = T_B = 9.1 N [1]`
b. At the same height, the string breaks, so to calculate the height, take average distance between A and B.
Height = `frac(H_A + H_B)(2) = frac(1.75 + 1)(2) = 1.375 m [1]`
To calculate the distance that A and B have been moved
`d_A = 1.75 – 1.375 = 0.375 m = d_B [1]`
Using SUVAT equation, we have:
`v^2 – u^2 = 2as`
`v = sqrt(2*3*0.375) = 1.5 ms^-1 [1]`
Choose direction is moving down of particle A:
s = ut + `1/2 g t^2`
The time of particle A hits the ground with u = +1.5 ms-1
`1.375 = 1.5t + 1/2 * g * t^2`
So `t_A = 0.395 s [1]`
The magnitude of velocity of A and B are the same but opposite sign, so at particle B:
`s = -ut + 1/2 g*t^2`
The time of particle B hits the ground with u = 1.5 ms-1
`1.375 = -1.5t + 1/2 * g * t^2`
So tB = 0.695s [1]
The difference in times = 0.695 – 0.395 = 0.3 s [1]
Question 11

Two blocks A and B of masses 4 kg and 5 kg respectively are joined by a light inextensible string. The blocks rest on a smooth plane inclined at an angle ? to the horizontal, where tan ? = `7/24`. The string is parallel to the line of greatest slope of the plane with B above A. A force of magnitude 36N acts on B, parallel to a line of greatest slope of the plane.
a. Find the acceleration of the blocks and tension in the string. [5]
b. At a particular instant, the speed of the blocks is 1ms-1. Find the time, after this instant, that it takes for the blocks to travel 0.65 m. [2]
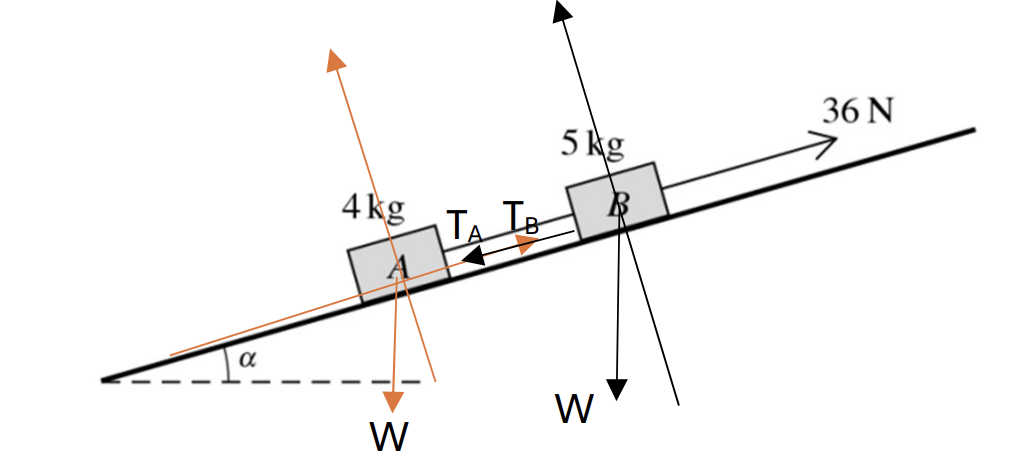
a. ? = tan-1(`7/24`) = 16.3o
Applying the Newton’s Second Law, we have:
At point A: `vec(F_(n et)) = vec(T_A) + vec(W_A)` (choose direction is to the right)
`Fnet = TA - mgsin 16.3`)`F_(n et) = T_A - mgsin 16.3`
`4a = T_A – 4 * 10 * sin16.3 (1) [1]`
At point B: `vec(F_(n et)) = vec(F_B) + vec(W_B) + vec(T_B)`
`ma = 36 – T_B - mgsin alpha`
`5a = 36 – T_B – 5 * 10 * sin16.3 (2) [1]`
Take (1) plus (2), we have:
`9a = 36 – 90*sin16.3 [1]`
a = `frac(36-90sin16.3)(9) = 1.19 ms^-2 [1]`
And the tension TA = `4 * 1.19 + 40*sin16.3 = 16N [1]`
`b. u = 1 ms^-1; s = 0.65m`
Applying the SUVAT equation, we have:
`s = ut + 1/2 * a * t^2 [1]`
`0.65 = 1t + 1/2 * 1.19 * t^2`
`t = 0.5 s or t = -2.18 s`
So the time it takes for the blocks to travel 0.65 m is 0.5 s. [1]
Question 12
A particle of mass 0.4 kg is released from rest at a height of 1.8 m above the surface of the water in a tank. There is no instantaneous change of speed when the particle enters the water. The water exerts an upward force of 5.6N on the particle when it is in the water.
a. Find the velocity of the particle at the instant when it reaches the surface of the water. [2]
b. Find the time that it takes from the instant when the particle enters the water until it comes to instantaneous rest in the water. You may assume that the tank is deep enough so that the praticle does not reach the bottom of the tank. [4]
c. Sketch a velocity-time graph for the motion of the particle from the instant at which it is released until it comes to instantaneous rest in the water. [3]
m = 0.4 kg; h = 1.8m; F = 5.6 N;
a. Applying the SUVAT equation, we have:
`v^2 – u^2 = 2as (with a = g = 10 ms^-2) [1]`
`v = sqrt(2 * 10 * 1.8 = 6 ms^-1) [1]`
b. Using Newton’s Second law for the particle in the vertical, we have:
`vec(F_(n et)) = vec(F_(exert)) + vec(W)`(choose direction moved down)
Fnet = - Fexert + W [1]
`0.4 * a = - 5.6 + 0.4 * 10`
`a = -4 ms^-2 [1]`
0 = 6 – 4t [1]
t = 1.5 s [1]
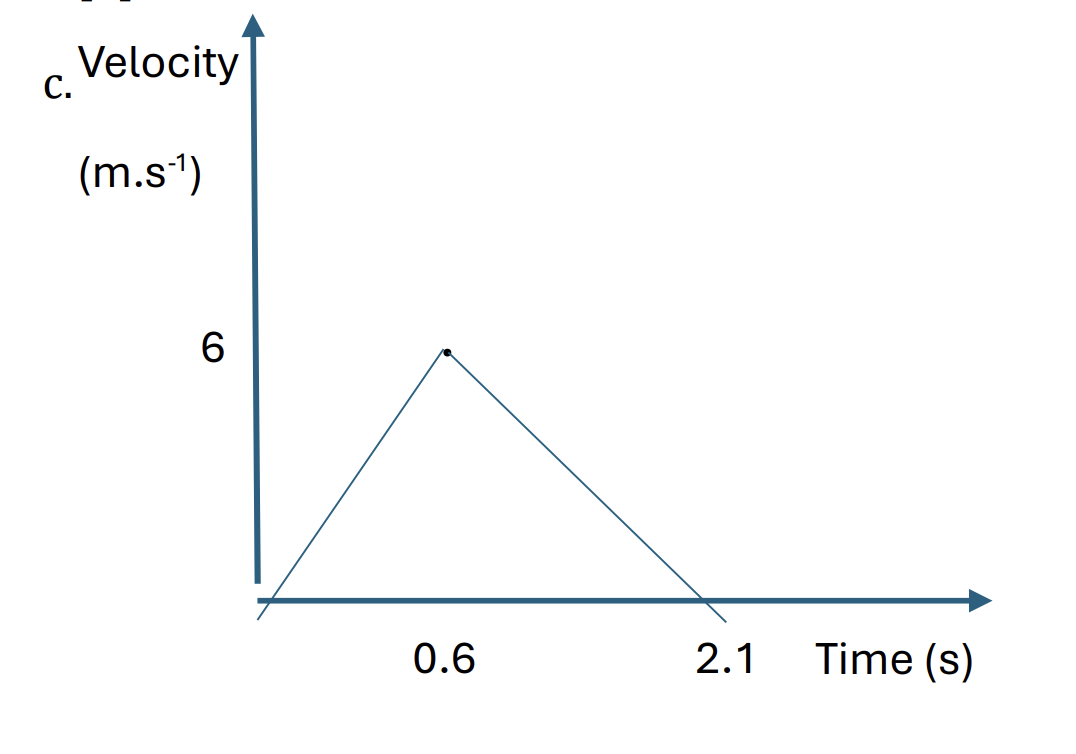
Question 13

Two particles P and W of masses 0.3 kg and 0.2 kg respectively, are attached to the ends of light inextensible string. The string passes over a ϐixed smooth pulley which is attached to the edge of a smooth plane. The plane is inclined at an angle `theta` to the horizontal, where sin`theta = 3/5` . P lies on the plane and Q hangs vertically below the pulley at a height of 0.8 m above the floor. The string between P and the pulley is parallel to a line of greatest slope of the plane. P is released from rest and Q moves vertically downwards.
a. Find the tension in the string and the magnitude of the acceleration of the particles. [5]
Q hits the floor and does not bounce. It is given that P does not reach the pulley in the subsequent motion.
b. Find the time, from the instant at which P is released, for Q to reach the floor. [2]
c. When Q hits the floor, the string becomes slack. Find the time, from the instant at which P is released, for the string to become taut again. [4]
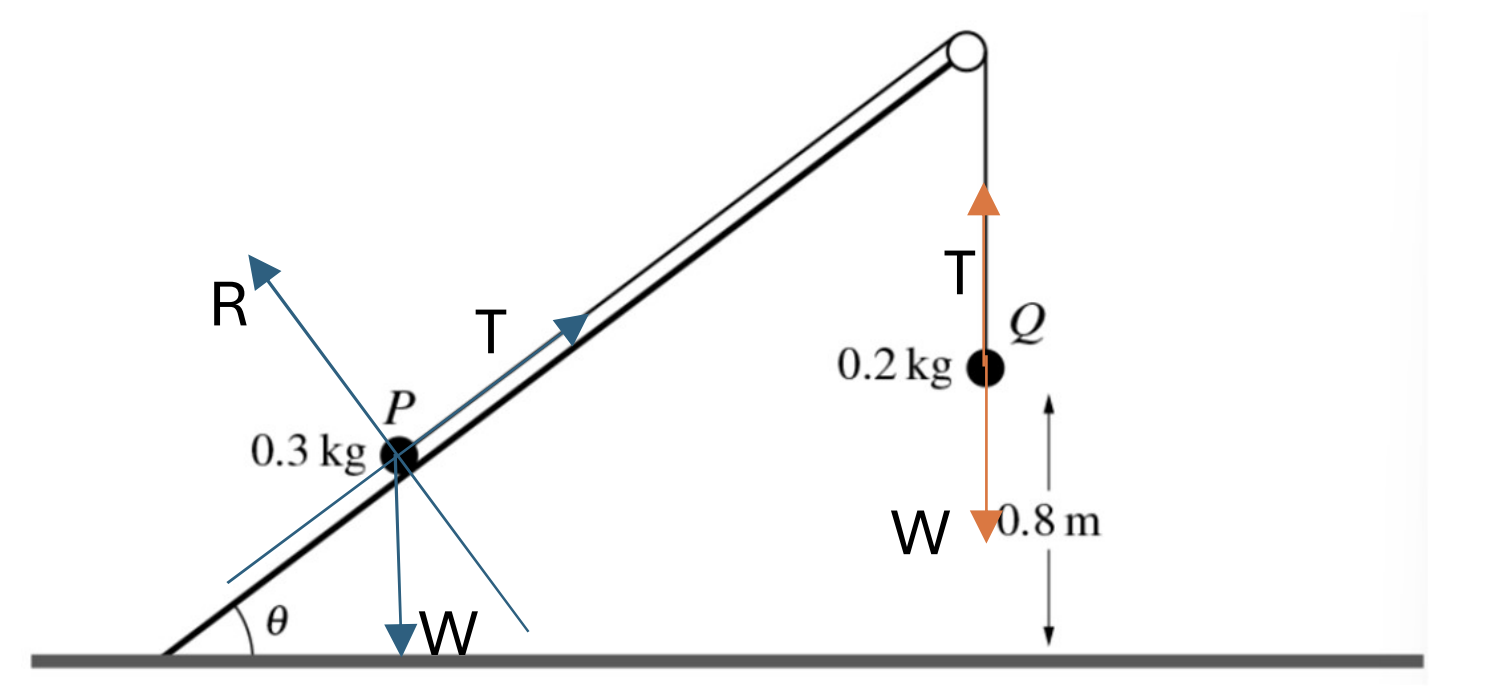
a. Applying the Newton’s Second Law, we have:
At point P:
`vec(F_( n et)) = vec(T) + vec(W)`(choose direction is to the right)
`F_(n et) = T – mgsintheta`
`ma + mgsintheta = T`
`0.3 * a = T – 0.3 * 10 * 3/5 (1) [1]`
At point Q:
`vec(F_(n et)) = vec(T) + vec(W)` (choose direction goes down)
Fnet = W - T
`0.2 * a = 0.2 * 10 - T`
`T = 2 - 0.2*a (2) [1]`
Substitute (2) into (1)
`0.38a = 2 - 0.2a - 1.8 [1]`
a = `frac(2-1.8)(0.5) = 0.4 ms^-2 [1]`
The tension is T = `2 – 0.2 * 0.4 = 1.92N [1]`
b. Applying SUVAT equation, we have:
`s = ut + 1/2 at^2 [1]`
`0.8 = 0 + 0.2t^2`
t = 2 s [1]
c. Speed when Q hits the floor
`v = u + at = 0 + 0.4 * 2 = 0.8 ms^-1`
Applying Newton’s second law, we have:
`-0.3 * g * 3/5 = 0.3 * a [1]`
a = -6 ms-2 [1]
`0 = 0.8t + 1/2 * (-6) * t^2`
t = 0.266 [1]
The total time when the instant at which P is released, for the string to become taut again: 2+ 0.266 = 2.27 s [1]
Question 14

Two particles A and B have masses m kg and km kg respectively, where k >1. The particles are attached to the ends of a light inextensible string. The string passes over a ϐixed smooth pulley and the partices hang vertically below it. Both particles are at a height of 0.81 m above horizontal ground. The system is released from rest and particle B reaches the ground 0.9 s later. Particle A does not reach the pulley in its subsequent motion.
a. Find the value of k and show that the tension in the string before B reaches the ground is equal to 12m N. [7]
At the instant when B reaches the ground, the string breaks.
b. Show that the speed of A when it reaches the ground is 5.97 ms-1, correct to 3 s.f, and find the time taken, after the string breaks, for A to reach the ground. [4]
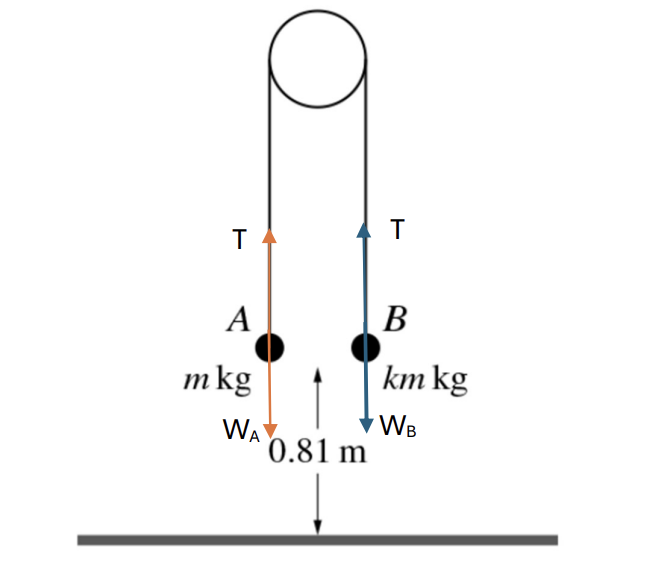
a. h = 0.81 m; t = 0.9s; u = 0 ms-1
At point A:
T – WA = ma
`T = m * 10 (1) [1]`
At point B:
`W_B - T = k*ma`
`T = k * m * 10 (2)[1]`
Take (1) + (2), we have:
`W_B – W_A = a*(m + k*m) [1]`
`k*m * 10 – m *10 = 2m*(k + 1)`
10k – 10 – 2k -2 = 0 [1]
8k = 12
k = 1.5 [1]
Substitute k = 1.5 into (1) [1]
`T = W_A + ma = 10m + 2m = 12m N [1]`
b. The velocity that B reached when it touched the ground, applying the SUVAT equation:
`v^2 – u^2 = 2as`
`v = sqrt(2* 2 * 0.81)= 1.8 ms^-1`
To find the velocity A when it reached the ground, we have some value of u = - 1.8 ms-1 (opposite direction with v); s = 1.62 m; a = g = 10 ms-2.
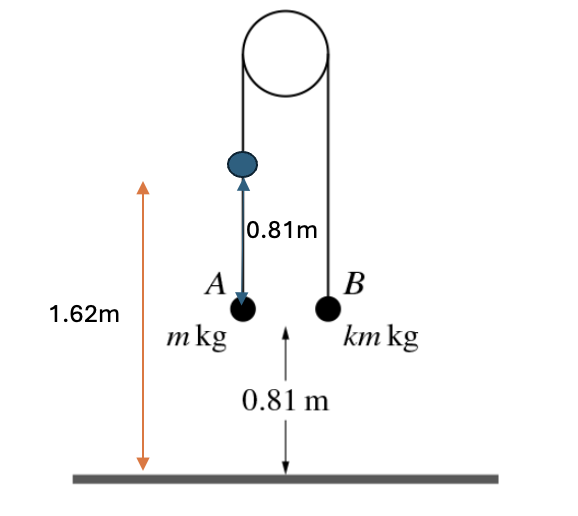
`v^2 – u^2= 2as`
`v = sqrt(1.8^2 + 2 * 10 * 1.62) = 5.97 ms^-1 [2]`
The time that after the string broke, A reached to the ground:
v = u + at
`5.97 = - 1.8 + 10 * t [1]`
`t = frac(5.97 - 1.8)(10) = - 0.78ms^-1`
Question 15

A particle P of mass 8 kg is on a smooth plane inclined at an angle of 30o to the horizontal. A force of magnitude 100N, making an angle of `theta^o` with a line of greatest slope and lying in the vertical plane containing the line of greatest slope, acts on P.
a. Given that P is in equilibrium, show that `theta` = 66.4, correct to 1 decimal place, and find the normal reaction between the plane and P. [4]
b. Given instead that `theta` = 30, find the acceleration of P. [2]
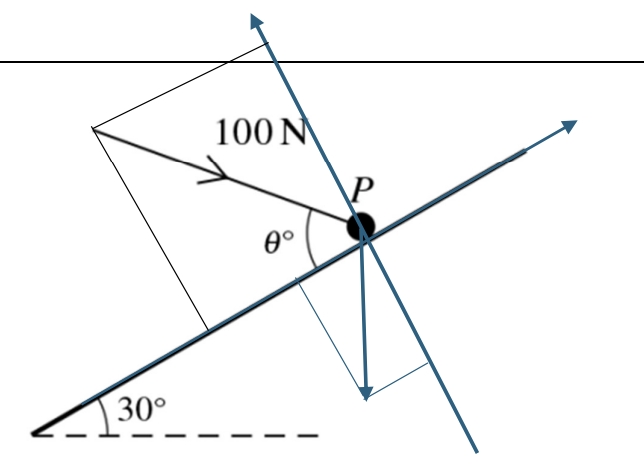
a. Because P is in the equilibrium, so we have the combination force as:
`m * g * sin30 –100 * costheta = 0 [1]`
`theta = cosfrac(8*10*sin30)(100) = 66.42^o [1]`
`R = 8 * 10* cos30 + 100 * sin 66.42 [1]`
R = 161 (N) [1]
b. Applying Newton’s 2nd law parallel to the plane
`100 cos 30 – 8 * 10 * sin30 = 8a [1]`
a = `frac(100cos30 - 8*10*sin30)(8) = 5.83 ms^-2 [1]`
Question 16

Two particles A and B have masses m kg and 0.1 kg respectively, where m > 0.1.
The particles are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley and the particles hang vertically below it. Both particles are at a height of 0.9 m above horizontal ground (see diagram).
The system is released from rest, and while both particles are in motion the tension in the string is 1.5 N. Particle B does not reach the pulley.
a. Find m. [4]
b. Find the speed at which A reaches the ground. [2]
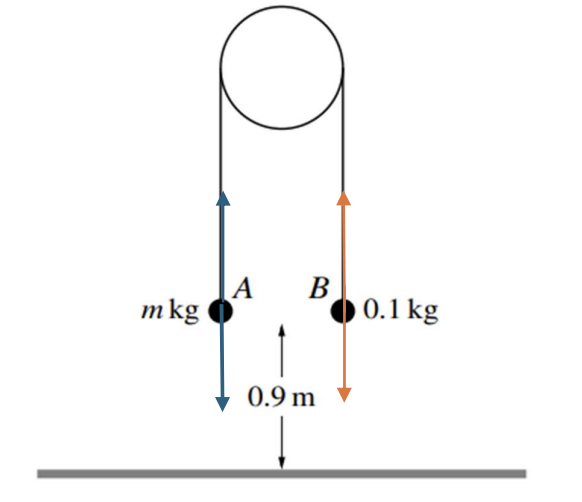
a. At point A: Choose direction is moving up
`T – 0.1 * g = 0.1 * a`
`T = 0.1 * a + 0.1 * 10 [1]`
Find the value of a:
1.5 = 0.1a + 1
`a = 5 ms^-2 [1]`
At point B: Choose direction is moving down
`m * g – T = m * a`
10m – 0.1a -1 = ma
10m - 0.5 -1 = 5m [1]
m = 0.3 kg [1]
b. Applying the SUVAT equation
`v^2 – v_o^2 = 2as (with u = 0 ms^-1) [1]`
`v = sqrt(2 * 5 * 0.9) = 3 ms^-1 [1]`
Question 17
A ring of mass 0.3 kg is threaded on a horizontal rough rod. The coefϐicient of friction between the ring and the rod is 0.8. A force of magnitude 8 N acts on the ring. This force acts at an angle of 100 above the horizontal in the vertical plane containing the rod.
Find the time taken for the ring to move, from rest, 0.6 m along the rod. [6]
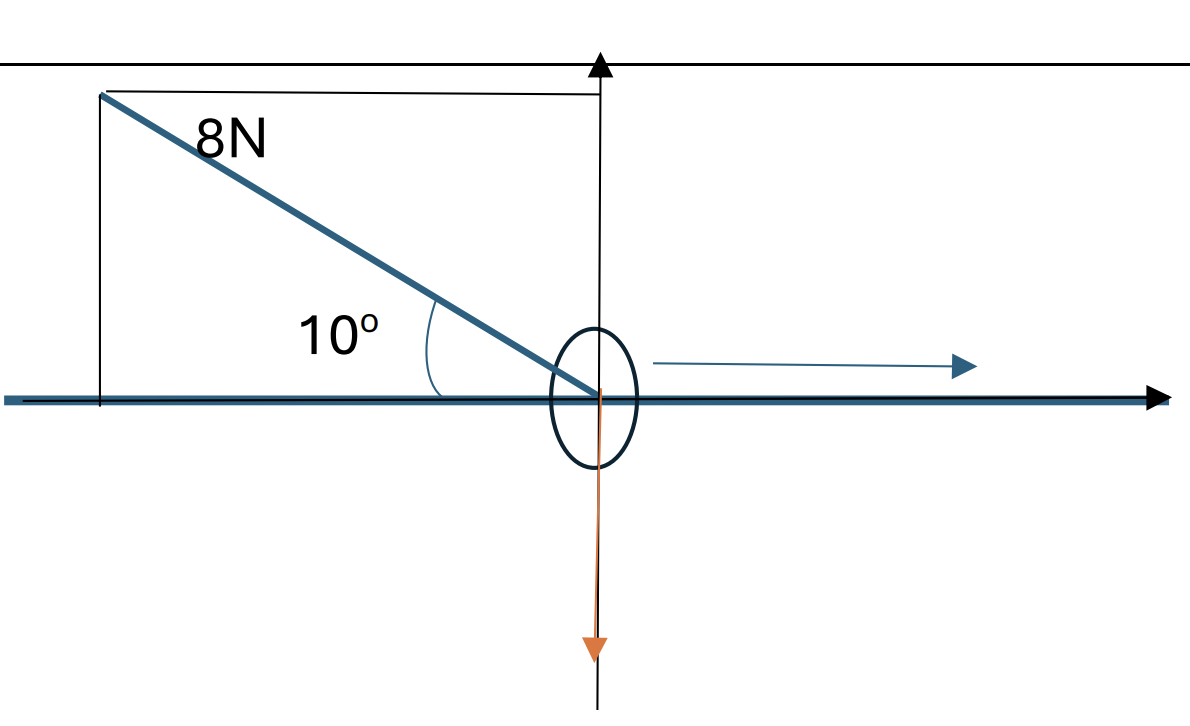
`R = 3 – 8*sin10 = 1.61 N [1]`
On the vertical line, we have the total force act:
`8sin10 + R = 0.3 * g`
On the horizontal line, we have the total force act
`8*cos10 – F = 0.3*a (with F = muR)`
`8*cos10 – 0.8 * 1.61 = 0.3*a [1]`
So a = `frac(8cos10 - 0.8*1.61)(0.3) = 21.97 ms^-2`
Applying the SUVAT equation, we have:
`s = v_ot + 1/2at^2 [1]`
`0.6 = 0 + 1/2 * 21.97 * t^2 [1]`
t = `sqrt(frac(0.6)(1/2 *21.97)) = 0.234 s [1]`
Question 18

A particle P of mass 0.3 kg rests on a rough plane inclined at an angle 1 to the horizontal, where `sintheta = 7/25` . A horizontal force of magnitude 4 N, acting in the vertical plane containing a line of greatest slope of the plane, is applied to P (see diagram). The particle is on the point of sliding up the plane.
a. Show that the coefficient of friction between the particle and the plane is `3/4` . [4]
The force acting horizontally is replaced by a force of magnitude 4 N acting up the plane parallel to a line of greatest slope.
b. Find the acceleration of P [3]
c. Starting with P at rest, the force of 4 N parallel to the plane acts for 3 seconds and is then removed. Find the total distance travelled until P comes to instantaneous rest. [3]
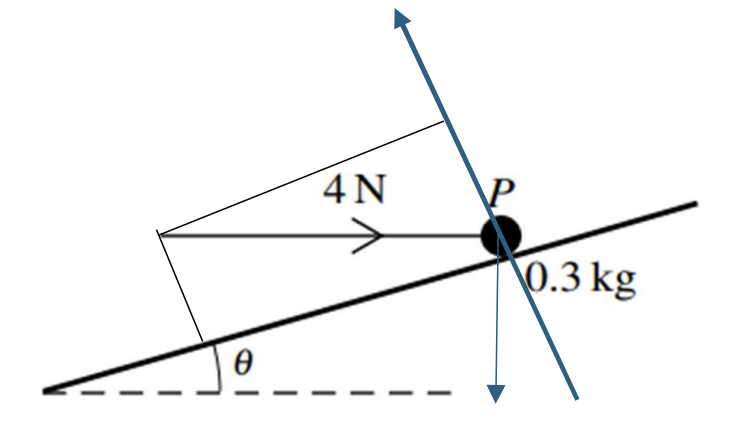
a. `R = 0.3 * g * costheta + 4 * sintheta = 3 * 24/25 + 4*7/25 [1]`
R = 4 N [1]
`F = 4 costheta – 0.3 * sintheta = 4 *sintheta - 4 *7/25`
F = 3N [1]
`F = mu *R`
`3 = mu * 4`
`→ mu = 3/4 [1]`
`b. F = mu * 0.3 * g * costheta = 3/4 * 3 * 24/25`= 2.16 N [1]
Using the Newton’s Second Law, we have:
`4 - 3/4 * 0.3 * g * 24/25 – 0.3 * g * 7/25 = 0.3 *a [1]`
`= 10/3 ms^-2 [1]`
`c. s_1 = 1/2 * 10/3 * 3^2 = 15 m and v = 10/3 * 3 = 10 ms^-1 [1]`
`–0.3 g * sin theta – mu * 0.3* g* cos θ = 0.3*a`
`-3 ×7/25 – 3/4 × 0.3 * 10 * 24/25 = 0.3*a`
a = `frac(-3 *7/25 - 3/4*0.3*10*24/25)(0.3) = -10 ms^-2 [1]`
Using the SUVAT equation, we have:
`s_2 = frac(0 - 10^2)(2*-10) = 5 m`
The total distance travelled until P comes to instantaneous rest:
`s_1 + s_2 = 15 + 5 = 20 m. [1]`
Question 19
Two particles A and B of masses 2.4 kg and 1.2 kg respectively, are connected by a light inextensible string which passes over a fixed smooth pulley. A is held at a distance of 2.1 m above a horizontal plane and B is 1.5 m above the plane. The particles hang vertically and are released from rest. In the subsequent motion A reaches the plane and does not rebound and B does not reach the pulley.
a. Show that the tension in the string before A reaches the plane is 16 N and find the magnitude of the acceleration of the particles before A reaches the plane. [4]
b. Find the greatest height of B above the plane. [3]
`a. 2.4 * g – T = 2.4* a`
`T – 1.2 * g = 1.2*a`
`2.4 g – 1.2 g = (2.4 + 1.2) a`
`T = 16 N and a = 10/3 ms^-2`
b. `v^2= 2*10/3* 2.1`
v = 3.741 ms-1
`0 = 14 – 2 * 10 * s`
`s = frac(-14)(-2*10) = 0.7m`
`s = 1.5 + 2.1 + 0.7 = 4.3 m`
Question 20
Two particles P and Q of masses 0.5 kg and 0.3 kg respectively, are connected by a light inextensible string. The string is taut, and P is vertically above Q. A force of magnitude 10 N is applied to P vertically upwards. Find the acceleration of the particles and the tension in the string connecting them. [5]
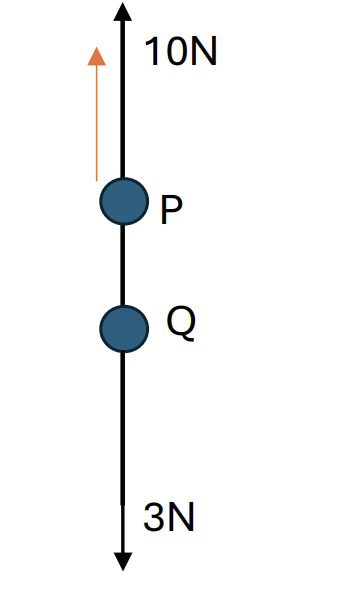
Use of Newton’s second law for P or Q or system
For P: `10 – 0.5 * g – T = 0.5 * a (1) [1]`
For Q: `T – 0.3 * g = 0.3* a (2) [1]`
Take (1) + (2), we have:
`10 – 0.8 * g = 0.8* a [1]`
a = `frac(10 - 0.8 *10)(0.8) = 2.5 ms^-2 [1]`
Use equation (1), we have:
`10 – 0.5 * 10 – T = 0.5 * 2.5`
T = 3.75 N. [1]
Question 1
a. Find the magnitude of the resultant force acting on a particle of mass 800g that would produce an acceleration of 3.1 ms-2 [1]
b. A particle of mass m kg has a deceleration of 4 ms-2 when acted upon by a resultant force of 5.2 kN. Find the value of m [1].
Question 2
A minibus of mass 1500 kg produces a driving force of 1125N. Given that the initial velocity of the minibus is 4 ms-2, find the time it takes the minibus to travel 385m along a straight horizontal road.
The coefficient of friction between the minibus and the road is 0.035 and the gravitational acceleration is given 9.8 m.s-2 [4]
Question 3
A car of mass 960 kg accelerates from 15 ms-1 to 30 ms-1 along a straight 400 m stretch of a horizontal motorway at a constant rate. During this acceleration, the engine produces a driving force of 1.24 kN. The motorist then spots a fault on the dashboard and decides to pull over onto the har shoulder, removing the driving force. The car then decelerates at a constant rate with a braking force of 500N.
Assuming that the frictional force is constant throughout, how much further does the car travel before it comes to rest? [4]
Question 4

Two particles A and B, of masses 3 m kg and 2 m kg respectively, are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley which is attached to the edge of a plane. The plane is inclined at an angle `theta` to the horizontal. A lies on the plane and B hangs vertically, 0.8 m above the floor, which is horizontal. The string between A and the pulley is parallel to a line of the greatest slope of the plane. Initially, A and B are at rest. (g = 10 ms-2)
a. Given that the plane is smooth, find the value of `theta` for which A remains at rest. [3] It is given instead that the plane is rough, `theta` = 30o and the acceleration of A up the plane is 0.1 ms-2.
b. Show that the coefficient of friction between A and the plane is `1/10 sqrt3`. [5]
c. When B reaches the floor it comes to rest. Find the length of time after B reaches the floor for which A is moving up the plane. (You may assume that A does not reach the pulley) [4]
Question 5
A car of mass 1400 kg is moving along a straight horizontal road against a resistance of magnitude 350N.
a. Find, in kW, the rate at which the engine of the car is working when it is traveling at a constant speed of 20 ms-1. [2]
b. Find the acceleration of the car when its speed is 20 ms-1 and the engine is working at 15 kW. [3]
Question 6

Two particles of masses 0.8 kg and 0.2 kg are connected by a light inextensible string that passes over a fixed smooth pulley. The system is released from rest with both particles 0.5 m above a horizontal floor (see diagram).
In the subsequent motion the 0.2 kg particle does not reach the pulley.
a. Show that the magnitude of the acceleration of the particles is 6 ms-2 and find the tension in the string. [4]
When the 0.8 kg particle reaches the floor it comes to rest.
b. Find the greatest height of the 0.2 kg particle above the floor. [3]
Question 7
A block of mass 5 kg is placed on a plane inclined at 30o to the horizontal. The coefficient of friction between the block and the plane is `mu`.

When a force of magnitude 40 N is applied to the block, acting up the plane parallel to a line of greatest slope, the block begins to slide up the plane.
Show that `mu < 1/5 sqrt3 [4]`

When a force of magnitude 40N is applied horizontally, in a vertical plane containing a line of greatest slope, the block does not move.
Show that, correct to 3 decimal places, the least possible value of `mu` is 0.152. [4]
Question 8

As shown in the diagram, particles A and B of masses 2 kg and 3 kg respectively are attached to the ends of a light inextensible string. The string passes over a smal ϐixed smooth pulley which is attached to the top of two inclined planes. Particle A is on plane P, which is inclined at an angle of 10o to the horizontal. Particle B is on plane Q, which is inclindes at an angle of 20o to the horizontal. The string is taut, and the two parts of the string are parallel to lines of greatest slope of their respective planes.
a. It is given that plane P is smooth, plane Q is rough, and the particles are in limiting equilibrium. Find the coefϐicient of friction between particle B and plane Q. [5]
b. It is given instead that both planes are smooth and that the particles are released from rest at the same horizontal level. [6]
Question 9
A constant resistance to motion of magnitude 350 N acts on a car of mass 1250 kg. The engine of the car exerts a constant driving force of 1200 N. The car travels a long a road inclined at an angle of ? to the horizontal, where sin`theta` = 0.05.
Find the speed of the car when it has moved 100m from rest in each of the following cases.
Question 10

Two particles A and B of masses 1.3 kg and 0.7 kg respectively, are connected by a light inextensible string which passes over smooth fixed pulley. Particle A is 1.75 m above the ϐloor and particle B is 1m above the floor.
The system is released from rest with the string taut, and the particle moves vertically. When the particles are at the same height the string breaks.
Question 11

Two blocks A and B of masses 4 kg and 5 kg respectively are joined by a light inextensible string. The blocks rest on a smooth plane inclined at an angle ? to the horizontal, where tan ? = `7/24`. The string is parallel to the line of greatest slope of the plane with B above A. A force of magnitude 36N acts on B, parallel to a line of greatest slope of the plane.
a. Find the acceleration of the blocks and tension in the string. [5]
b. At a particular instant, the speed of the blocks is 1ms-1. Find the time, after this instant, that it takes for the blocks to travel 0.65 m. [2]
Question 12
A particle of mass 0.4 kg is released from rest at a height of 1.8 m above the surface of the water in a tank. There is no instantaneous change of speed when the particle enters the water. The water exerts an upward force of 5.6N on the particle when it is in the water.
a. Find the velocity of the particle at the instant when it reaches the surface of the water. [2]
b. Find the time that it takes from the instant when the particle enters the water until it comes to instantaneous rest in the water. You may assume that the tank is deep enough so that the praticle does not reach the bottom of the tank. [4]
c. Sketch a velocity-time graph for the motion of the particle from the instant at which it is released until it comes to instantaneous rest in the water. [3]
Question 13

Two particles P and W of masses 0.3 kg and 0.2 kg respectively, are attached to the ends of light inextensible string. The string passes over a ϐixed smooth pulley which is attached to the edge of a smooth plane. The plane is inclined at an angle `theta` to the horizontal, where sin`theta = 3/5` . P lies on the plane and Q hangs vertically below the pulley at a height of 0.8 m above the floor. The string between P and the pulley is parallel to a line of greatest slope of the plane. P is released from rest and Q moves vertically downwards.
a. Find the tension in the string and the magnitude of the acceleration of the particles. [5]
Q hits the floor and does not bounce. It is given that P does not reach the pulley in the subsequent motion.
b. Find the time, from the instant at which P is released, for Q to reach the floor. [2]
c. When Q hits the floor, the string becomes slack. Find the time, from the instant at which P is released, for the string to become taut again. [4]
Question 14

Two particles A and B have masses m kg and km kg respectively, where k >1. The particles are attached to the ends of a light inextensible string. The string passes over a ϐixed smooth pulley and the partices hang vertically below it. Both particles are at a height of 0.81 m above horizontal ground. The system is released from rest and particle B reaches the ground 0.9 s later. Particle A does not reach the pulley in its subsequent motion.
a. Find the value of k and show that the tension in the string before B reaches the ground is equal to 12m N. [7]
At the instant when B reaches the ground, the string breaks.
b. Show that the speed of A when it reaches the ground is 5.97 ms-1, correct to 3 s.f, and find the time taken, after the string breaks, for A to reach the ground. [4]
Question 15

A particle P of mass 8 kg is on a smooth plane inclined at an angle of 30o to the horizontal. A force of magnitude 100N, making an angle of `theta^o` with a line of greatest slope and lying in the vertical plane containing the line of greatest slope, acts on P.
a. Given that P is in equilibrium, show that `theta` = 66.4, correct to 1 decimal place, and find the normal reaction between the plane and P. [4]
b. Given instead that `theta` = 30, find the acceleration of P. [2]
Question 16

Two particles A and B have masses m kg and 0.1 kg respectively, where m > 0.1.
The particles are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley and the particles hang vertically below it. Both particles are at a height of 0.9 m above horizontal ground (see diagram).
The system is released from rest, and while both particles are in motion the tension in the string is 1.5 N. Particle B does not reach the pulley.
a. Find m. [4]
b. Find the speed at which A reaches the ground. [2]
Question 17
A ring of mass 0.3 kg is threaded on a horizontal rough rod. The coefϐicient of friction between the ring and the rod is 0.8. A force of magnitude 8 N acts on the ring. This force acts at an angle of 100 above the horizontal in the vertical plane containing the rod.
Find the time taken for the ring to move, from rest, 0.6 m along the rod. [6]
Question 18

A particle P of mass 0.3 kg rests on a rough plane inclined at an angle 1 to the horizontal, where `sintheta = 7/25` . A horizontal force of magnitude 4 N, acting in the vertical plane containing a line of greatest slope of the plane, is applied to P (see diagram). The particle is on the point of sliding up the plane.
a. Show that the coefficient of friction between the particle and the plane is `3/4` . [4]
The force acting horizontally is replaced by a force of magnitude 4 N acting up the plane parallel to a line of greatest slope.
b. Find the acceleration of P [3]
c. Starting with P at rest, the force of 4 N parallel to the plane acts for 3 seconds and is then removed. Find the total distance travelled until P comes to instantaneous rest. [3]
Question 19
Two particles A and B of masses 2.4 kg and 1.2 kg respectively, are connected by a light inextensible string which passes over a fixed smooth pulley. A is held at a distance of 2.1 m above a horizontal plane and B is 1.5 m above the plane. The particles hang vertically and are released from rest. In the subsequent motion A reaches the plane and does not rebound and B does not reach the pulley.
a. Show that the tension in the string before A reaches the plane is 16 N and find the magnitude of the acceleration of the particles before A reaches the plane. [4]
b. Find the greatest height of B above the plane. [3]
Question 20
Two particles P and Q of masses 0.5 kg and 0.3 kg respectively, are connected by a light inextensible string. The string is taut, and P is vertically above Q. A force of magnitude 10 N is applied to P vertically upwards. Find the acceleration of the particles and the tension in the string connecting them. [5]