Question 1
A vase is pushed 1.6 m across a horizontal table by a horizontal force of 8N.
a. Find the work done by the force in pushing the vase [1]
b. Find the work done if the force acts at an angle of 30o to horizontal instead. [1]a. Work done is given by the formula Wd = F.d WD = 8 x 1.6 = 12.8 J [1] b. Applying the formula for work done by against a force acting at an angle of ? is Work done (WD) = Fdcos ? WD = 8 x 1.6 cos30 = 11.1 J [1]
Easy
Mark as Complete
Mark Scheme
Question 2
A package of mass 23kg is pulled 5m at a constant speed across a rough horizontal floor in an airport by a cord at an angle of sin-1(`7/25` ) above the horizontal. Given that the work done against friction is 240J.
Find the coefficient of friction between the package and the floor. [5]
Easy
Mark as Complete
Mark Scheme
Question 3
A cart of mass 8 kg is pushed 15 m up a rough plane inclined at an angle of 14o. The coefficient of friction between the cart and the plane `1/16`.
Find the total work done. [4]
Medium
Mark as Complete
Mark Scheme
Question 4
The intial velocity of buggy of mass 25 kg is 28ms-1.
Find the change in kinetic energy of the buggy after it decelerates at 1.6 ms-1 for 5s, stating whether it is an increase or a decrease.
Easy
Mark as Complete
Mark Scheme
Question 5
A flowerpot of mass 800g falls from a shelf 240 cm above the ground.
Find the loss of potential energy of the flowerpot.
Easy
Mark as Complete
Mark Scheme
Question 6
A rocket of mass 3kg is launched from the ground at 32 ms-1 and travels vertically.
Find the maximum height reached by the rocket by using:
a. The equation of uniformly accelerated motion
b. The change in energy
Easy
Mark as Complete
Mark Scheme
Question 7
A car of mass 1800 kg is towing a trailer of mass 400kg along a straight horizontal road. The car and trailer are connected by a light rigid tow-bar. The car is accelerating at 1.5 ms-2. There are constant resistance forces of 250N on the car and 100N on the trailer.
a. Find the tension in the tow-bar. [2]
b. Find the power of the engine of the car at the instant when the speed is 20 ms-1. [3]
Easy
Mark as Complete
Mark Scheme
Question 8
A child of mass 35 kg is swinging on a rope. The child is modelled as a particle P and the rope if modeled as a light inextensible string of length 4m. Initially P is held at an angle of 45o to the vertical (see diagram).
a. Given that there is no resistance force, find the speed of P when it has traveled halfway along the circular arc from its initial position to its lowest point [4].
b. It is given instead that there is a resistance force. The work done against the resistance force as P travels from its initial position to its lowest point is X J. The speed of P at its lowest point is 4 ms-1.
Find X [3].
Easy
Mark as Complete
Mark Scheme
Question 9
A car of mass 1250 kg is moving on a straight road. On a horizontal section of the road, the car has a constant speed of 32 ms−1 and there is a constant force of 750 N resisting the motion.
a. Calculate, in kW, the power developed by the engine of the car. [2]
i. Given that this power is suddenly decreased by 8 kW, find the instantaneous deceleration of the car. [3]
ii. On a section of the road inclined at sin−10.096 to the horizontal, the resistance to the motion of the car is (1000 + 8v) N when the speed of the car is v m s−1. The car travels up this section of the road at constant speed with the engine working at 60 kW.
Find this constant speed. [5]
Medium
Mark as Complete
Mark Scheme
Question 10
A block B of mass 4 kg is pushed up a line of greatest slope of a smooth plane inclined at 30o to
the horizontal by a force applied to B, acting in the direction of motion of B. The block passes through points P and Q with speeds 12 ms−1 and 8 ms−1 respectively. P and Q are 10 m apart with P below the level of Q.
a. Find the decrease in kinetic energy of the block as it moves from P to Q [2]
b. Hence find the work done by the force pushing the block up the slope as the block moves from P to Q. [3]
c. At the instant the block reaches Q, the force pushing the block up the slope is removed. Find the time taken, after this instant, for the block to return to P. [4]
Medium
Mark as Complete
Mark Scheme
Question 11
A car of mass 1500 kg is pulling a trailer of mass 750 kg up a straight hill of length 800 m inclined at an angle of sin−1 0.08 to the horizontal. The resistances to the motion of the car and trailer are 400 N and 200 N respectively. The car and trailer are connected by a light rigid tow-bar. The car and trailer have speed 30 m s−1 at the bottom of the hill and 20 m s−1 at the top of the hill.
a. Use an energy method to find the constant driving force as the car and trailer travel up the hill. [5]
After reaching the top of the hill the system consisting of the car and trailer travels along a straight level road. The driving force of the car’s engine is 2400 N and the resistances to motion are unchanged.
b. Find the acceleration of the system and the tension in the tow-bar. [4]
Hard
Mark as Complete
Mark Scheme
Question 12
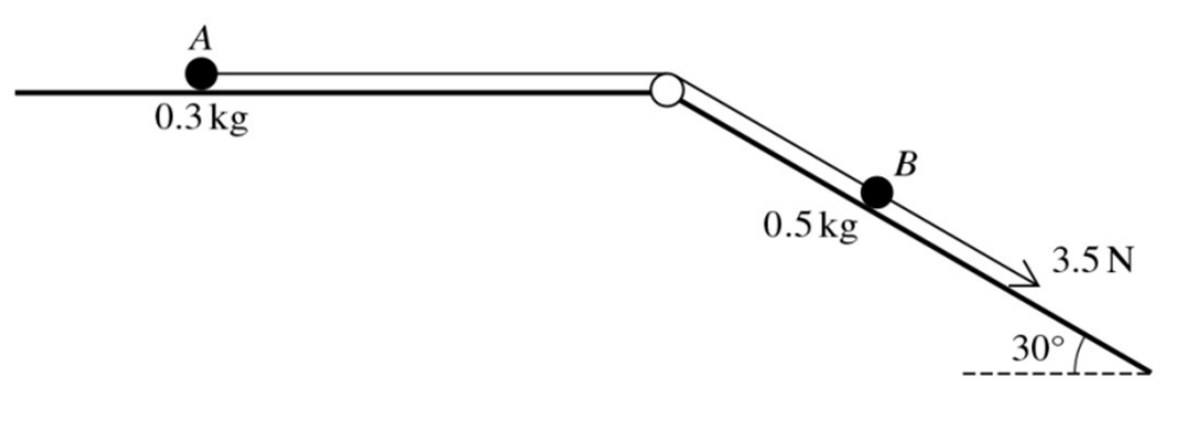
Two particles A and B, of masses 0.3 kg and 0.5 kg respectively, are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley which is attached to a horizontal plane and to the top of an inclined plane. The particles are initially at rest with A on the horizontal plane and B on the inclined plane, which makes an angle of 30o with the horizontal. The string is taut and B can move on a line of greatest slope of the inclined plane. A force of magnitude 3.5 N is applied to B acting down the plane (see diagram).
a. Given that both planes are smooth, ϐind the tension in the string and the acceleration of B. [5]
b. It is given instead that the two planes are rough. When each particle has moved a distance of 0.6 m from rest, the total amount of work done against friction is 1.1 J. Use an energy method to ϐind the speed of B when it has moved this distance down the plane. [You should assume that the string is sufficiently long so that A does not hit the pulley when it moves 0.6 m. [4]
Medium
Mark as Complete
Mark Scheme
Question 13
A box of mass 5 kg is pulled at a constant speed a distance of 15 m up a rough plane inclined at an angle of 20o to the horizontal. The box moves along a line of greatest slope against a frictional force of 40 N.
The force pulling the box is parallel to the line of greatest slope.
a. Find the work done against friction. [1]
b. Find the change in gravitational potential energy of the box. [2]
c. Find the work done by the pulling force. [1]
Easy
Mark as Complete
Mark Scheme
Question 14
A car of mass 1600 kg is pulling a caravan of mass 800 kg. The car and the caravan are connected by a light rigid tow-bar. The resistances to the motion of the car and caravan are 400 N and 250 N respectively.
a. The car and caravan are travelling along a straight horizontal road.
i. Given that the car and caravan have a constant speed of 25 m s−1, find the power of the car’s engine. [2]
ii. The engine’s power is now suddenly increased to 39 kW. Find the instantaneous acceleration of the car and caravan and find the tension in the tow-bar. [5]
b.The car and caravan now travel up a straight hill, inclined at an angle of sin−1 0.05 to the horizontal, at a constant speed of v m s−1 . The car’s engine is working at 32.5 kW. Find v. [3]
Hard
Mark as Complete
Mark Scheme
Question 15
A car of mass 1500 kg is pulling a trailer of mass 300 kg along a straight horizontal road at a constant speed of 20 m s−1. The system of the car and trailer is modelled as two particles, connected by a light rigid horizontal rod. The power of the car’s engine is 6000 W. There are constant resistances to motion of R N on the car and 80 N on the trailer.
a. Find the value of R. [2]
The power of the car’s engine is increased to 12 500 W. The resistance forces do not change.
b. Find the acceleration of the car and trailer and the tension in the rod at an instant when the speed of the car is 25 m s−1. [5]
Medium
Mark as Complete
Mark Scheme
Question 16
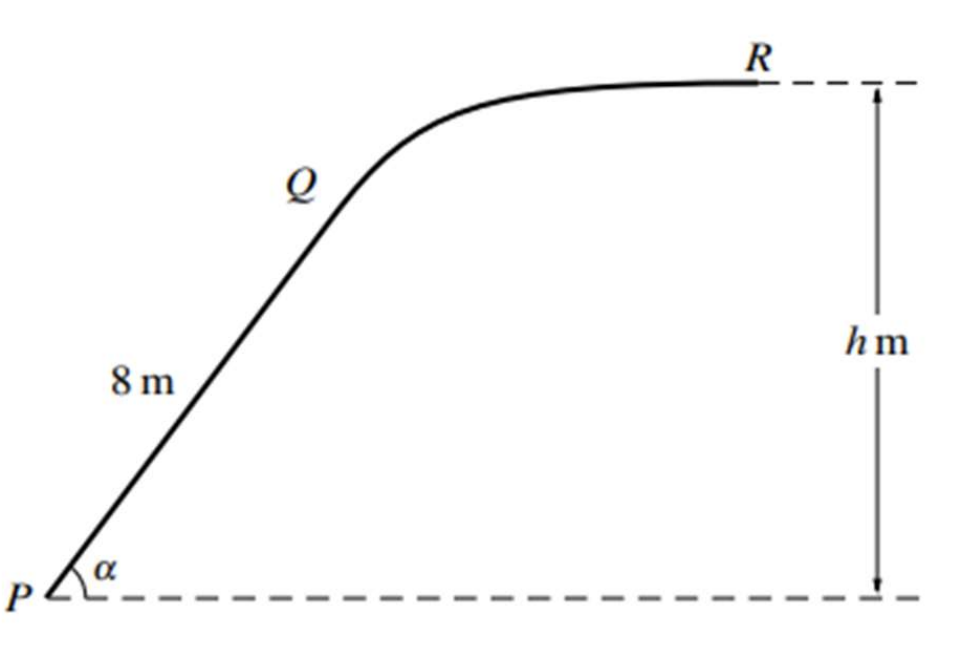
The diagram shows the vertical cross-section PQR of a slide. The part PQ is a straight line of length 8 m inclined at angle `alpha` to the horizontal, where sin`alpha`= 0.8. The straight part PQ is tangential to the curved part QR, and R is h m above the level of P. The straight part PQ of the slide is rough and the curved part QR is smooth. A particle of mass 0.25 kg is projected with speed 15 m s−1 from P towards Q and comes to rest at R. The coefficient of friction between the particle and PQ is 0.5.
a. Find the work done by the friction force during the motion of the particle from P to Q. [4]
b. Hence find the speed of the particle at Q. [4]
c. Find the value of h. [3]
Medium
Mark as Complete
Mark Scheme
Question 17
A lorry has mass 12 000 kg.
a. The lorry moves at a constant speed of 5 m s−1 up a hill inclined at an angle of `theta`o to the horizontal, where sin-1 = 0.08. At this speed, the magnitude of the resistance to motion on the lorry is 1500 N. Show that the power of the lorry’s engine is 55.5 kW. [3]
When the speed of the lorry is v m s−1 the magnitude of the resistance to motion is kv2 N, where k is a constant.
b. Show that k = 60. [1]
c. The lorry now moves at a constant speed on a straight level road. Given that its engine is still working at 55.5 kW, find the lorry’s speed. [3]
Medium
Mark as Complete
Mark Scheme
Question 18
A particle of mass 1.3 kg rests on a rough plane inclined at an angle `theta`o to the horizontal, where tan`alpha = 12/5`. The coefficient of friction between the particle and the plane is `mu`.
a. A force of magnitude 20 N parallel to a line of greatest slope of the plane is applied to the particle and the particle is on the point of moving up the plane.
Show that `mu` = 1.6. [4]
b. The force of magnitude 20 N is now removed.
Find the acceleration of the particle. [2]
c. Find the work done against friction during the first 2 s of motion. [3]
Medium
Mark as Complete
Mark Scheme
Question 19
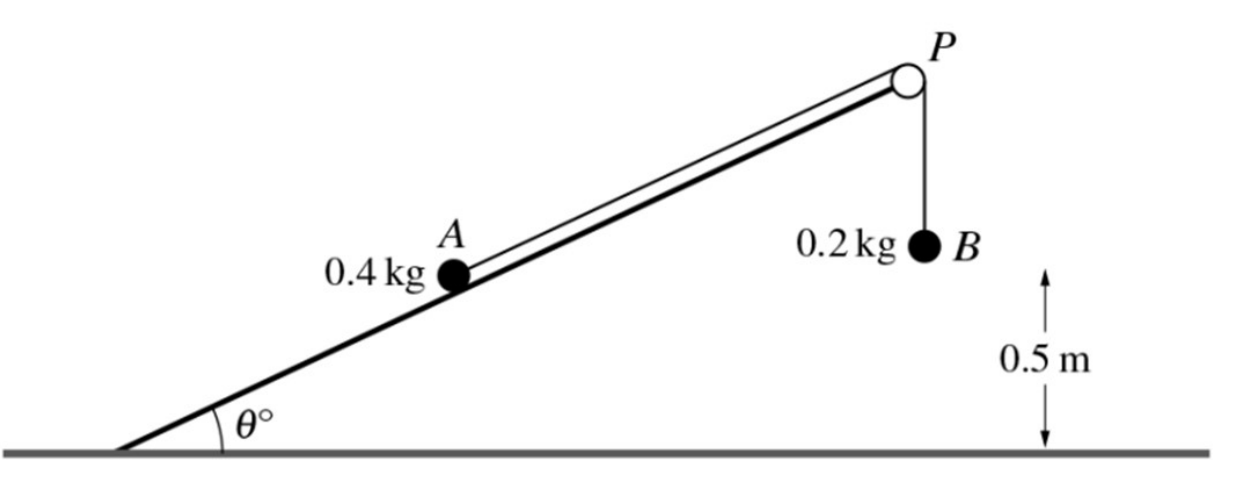
Two particles A and B, of masses 0.4 kg and 0.2 kg respectively, are connected by a light inextensible string. Particle A is held on a smooth plane inclined at an angle of `theta`o to the horizontal. The string passes over a small smooth pulley P fixed at the top of the plane, and B hangs freely 0.5 m above horizontal ground (see diagram). The particles are released from rest with both sections of the string taut.
a. Given that the system is in equilibrium, find `theta`. [3]
b. It is given instead that `theta` = 20. In the subsequent motion particle A does not reach P and B remains at rest after reaching the ground.
i. Find the tension in the string and the acceleration of the system. [4]
ii. Find the speed of A at the instant B reaches the ground. [2]
iii. Use an energy method to ϐind the total distance A moves up the plane before coming to instantaneous rest. [5]
Hard
Mark as Complete
Mark Scheme
Question 20
A car has mass 1000 kg. When the car is travelling at a steady speed of vm s−1, where v > 2, the resistance to motion of the car is (Av + B) N, where A and B are constants.
The car can travel along a horizontal road at a steady speed of 18 m s−1 when its engine is working at 36 kW.
The car can travel up a hill inclined at an angle of 1 to the horizontal, where sin-1 = 0.05, at a steady speed of 12 m s−1 when its engine is working at 21 kW.
Find A and B. [7].
Hard
Mark as Complete
Mark Scheme
Question 1
A vase is pushed 1.6 m across a horizontal table by a horizontal force of 8N.
a. Find the work done by the force in pushing the vase [1]
b. Find the work done if the force acts at an angle of 30o to horizontal instead. [1]a. Work done is given by the formula Wd = F.d WD = 8 x 1.6 = 12.8 J [1] b. Applying the formula for work done by against a force acting at an angle of ? is Work done (WD) = Fdcos ? WD = 8 x 1.6 cos30 = 11.1 J [1]
a. Work done is given by the formula `WD = F*d`
`WD = 8 * 1.6 = 12.8 J`[1`
b. Applying the formula for work done by against a force acting at an angle of `theta`
Work done (WD) = `F*d*costheta`
`WD = 8 * 1.6 cos30 = 11.1 J [1]`
Question 2
A package of mass 23kg is pulled 5m at a constant speed across a rough horizontal floor in an airport by a cord at an angle of sin-1(`7/25` ) above the horizontal. Given that the work done against friction is 240J.
Find the coefficient of friction between the package and the floor. [5]
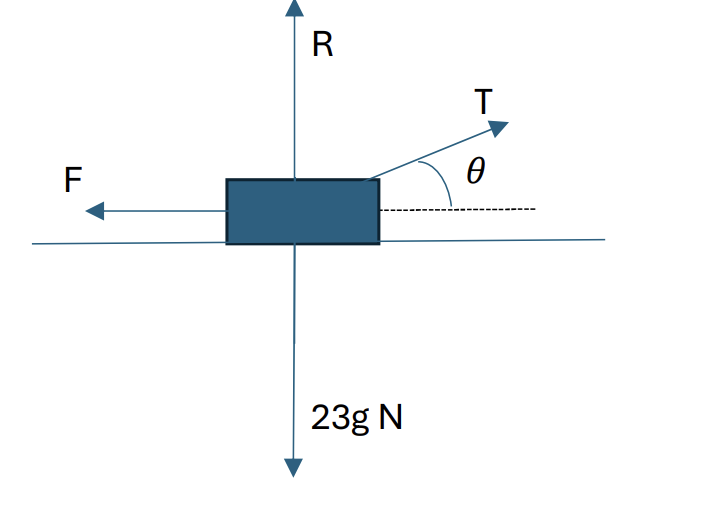
The work done against the frictional force, WD = Fd
`F = frac(WD)(d) = 240/5 = 48N [1]`
Resolve horizontally in the direction of motion. (moves to right)
`T*costheta – F = 0`
`F = Tcostheta`
Given that `sintheta = 7/25`, use trigonometry to ϐind the value of `costheta`
The adjacent is `sqrt((25^2) - 7^2)` = 24 [1]
Hence `costheta` = `24/25`
T = `F/costheta`= `48/(24/25` = 50 N [1]
Resolve vertically (goes up)
`R + Tsintheta – mg = 0`
`R = mg - Tsintheta – mg = 0`
`R mg - Tsintheta = 23 * 1 - 50*7/25 = 230 - 14 = 216 N [1]`
Finally, apply the formula F `= mu R`
`mu = F/R = 48/216 = 2/9 [1]`
Question 3
A cart of mass 8 kg is pushed 15 m up a rough plane inclined at an angle of 14o. The coefficient of friction between the cart and the plane `1/16`.
Find the total work done. [4]
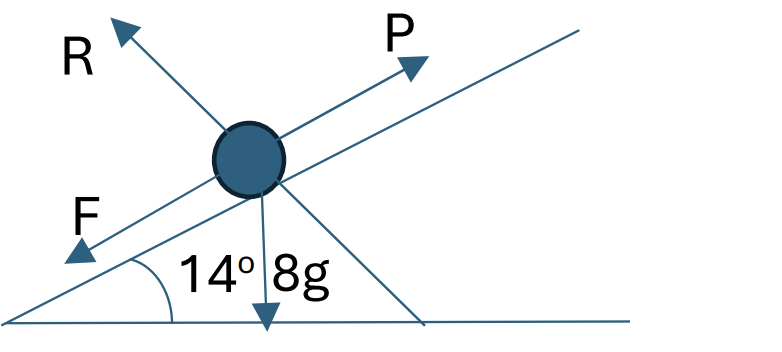
Work is done against both friction and gravity. For the work done against friction, you need to know the frictional force. Find R by resolving perpendicular to the surface, then apply `F = muR`.
`R = mgcostheta`
Using `F = muR, F = mumgcostheta`
`F = 1/16 * 8 * 10 * cos 14 = 4.851 N [1]`
`WD = F*d = 4.85 * 15 = 72. 77 J [1]`
For the work done against gravity, you need to know the height. The height can be found by using trigonometry
h is the opposite and d is the hypotenuse. Hence `h = sintheta`
`h = dsintheta = 15sin14 = 3.629 [1]`
WD = 290.3 J
Total work done = 72. 77 _ 290.3 = 363 J [1]
Question 4
The intial velocity of buggy of mass 25 kg is 28ms-1.
Find the change in kinetic energy of the buggy after it decelerates at 1.6 ms-1 for 5s, stating whether it is an increase or a decrease.
The formula for change in kinetic energy is given by change in
`KE = 1/2 *m * (v^2 – u^2)`
You know that m = 25 kg and u = 28 ms-1 but you do not know the value of v.
You are given that u = 28ms-1, a = -1.6 ms-2 and t = 5 s.
Since you need v, you can substitute in the formula v = u + at.
v = u + at
`= 28 – 1.6 * 6 = 20 ms^-1`
Change in KE = `1/2*m*(v^2 - u^2) = 1/2 *25 * (20^2 - 28^2)`
= -4800J
This is a decrease of 4800J, which could also be written as 4.8 kJ.
Question 5
A flowerpot of mass 800g falls from a shelf 240 cm above the ground.
Find the loss of potential energy of the flowerpot.
The change in potential is given by change in PE = mgh.
You are given that m = 0.8 kg and h = 2.4 m
Change in PE = mgh = `0.8 *10 * 2.4 = 19.2J`
Question 6
A rocket of mass 3kg is launched from the ground at 32 ms-1 and travels vertically.
Find the maximum height reached by the rocket by using:
a. The equation of uniformly accelerated motion
b. The change in energy
a. u = 32 ms-1, v = 0 ms-1, a = 10 ms-2
Applying the Suvat equation:
`v^2 = u^2 + 2as`
`s = frac(v^2 - u^2)(2a) = frac(0^2 - 32^2)(2 * -10) = -102/-20 = 51.2 m`
b. The change in kinetic energy is given by
`1/2*m*(v^2 -u^2) = 1/2 * 3 *(0^2 - 32^2) = - 1536 J`
Assume that the kinetic energy lost is all conveyed into a gain in potential energy. The gain in potential energy is given by mgh.
`1536 = 3 * 10 * h`
`h = 1536/30 = 51.2 m`
Question 7
A car of mass 1800 kg is towing a trailer of mass 400kg along a straight horizontal road. The car and trailer are connected by a light rigid tow-bar. The car is accelerating at 1.5 ms-2. There are constant resistance forces of 250N on the car and 100N on the trailer.
a. Find the tension in the tow-bar. [2]
b. Find the power of the engine of the car at the instant when the speed is 20 ms-1. [3]
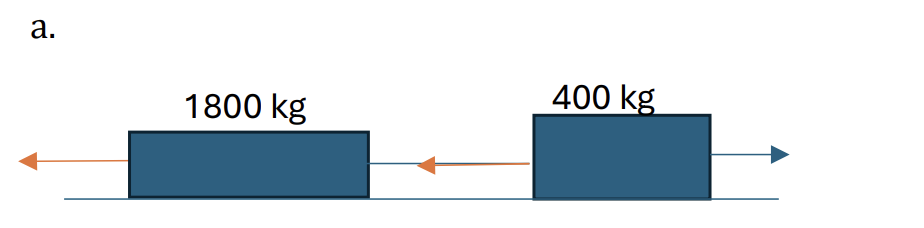
Apply the Newton’s Second Law on the trailer, we have:
`vec(T) + vec(R) = mveca` (choose direction is moved to the left) [1]
T – R = ma
`T = R + ma = 100 + 400* 1.5 = 700N [1]`
b. Using Newton’s Second Law for the system contains the car and trailer:
`F – 250 – 100 = 2200 * 1.5`
F = 3650 N [1]
For the use of power = `F*v`[1]
`P = 3650 * 20 = 73 kW [1]`
Question 8
A child of mass 35 kg is swinging on a rope. The child is modelled as a particle P and the rope if modeled as a light inextensible string of length 4m. Initially P is held at an angle of 45o to the vertical (see diagram).
a. Given that there is no resistance force, find the speed of P when it has traveled halfway along the circular arc from its initial position to its lowest point [4].
b. It is given instead that there is a resistance force. The work done against the resistance force as P travels from its initial position to its lowest point is X J. The speed of P at its lowest point is 4 ms-1.
Find X [3].
a. Attempt at finding PE lost [1]
`PE lost = 35*g (4*cos22.5 – 4*cos45) [1]`
`1/2 * 35 * v^2 = 35*g (4cos22.5 - 4 cos45) [1]`
Speed = 4.16 ms–1 [1]
b. Use of the work-energy equation in the form: PE lost = KE gain + WD against resistance [1]
`1/2 * 35 * 4^2 = 35*g*(4 -4 cos45) - X [1]`
X = 130 J [1]
Question 9
A car of mass 1250 kg is moving on a straight road. On a horizontal section of the road, the car has a constant speed of 32 ms−1 and there is a constant force of 750 N resisting the motion.
a. Calculate, in kW, the power developed by the engine of the car. [2]
i. Given that this power is suddenly decreased by 8 kW, find the instantaneous deceleration of the car. [3]
ii. On a section of the road inclined at sin−10.096 to the horizontal, the resistance to the motion of the car is (1000 + 8v) N when the speed of the car is v m s−1. The car travels up this section of the road at constant speed with the engine working at 60 kW.
Find this constant speed. [5]
a. DF = 750 N [1]
`i. Power = (750)* 32 = 24kW [1]`
`ii. 16000 = DF * 32 [1]`
DF = 500 N
`500 – 750 = 1250 * a [1]`
`a = - 0.2 ms^-2 [1]`
`DF = 1000 + 8*v + 1250 * 10 * 0.096 [1]`
2200 + 8v [1]
`600000 = (2200 + 8v) * v [1]`
`8*v^2 + 2200*v – 60000 = 0 [1]`
v = 24 ms-1 [1]
Question 10
A block B of mass 4 kg is pushed up a line of greatest slope of a smooth plane inclined at 30o to
the horizontal by a force applied to B, acting in the direction of motion of B. The block passes through points P and Q with speeds 12 ms−1 and 8 ms−1 respectively. P and Q are 10 m apart with P below the level of Q.
a. Find the decrease in kinetic energy of the block as it moves from P to Q [2]
b. Hence find the work done by the force pushing the block up the slope as the block moves from P to Q. [3]
c. At the instant the block reaches Q, the force pushing the block up the slope is removed. Find the time taken, after this instant, for the block to return to P. [4]
a. Decrease in KE = `1/2 * m * (v^2 - u^2) [1]`
= `1/2 * 4 * ( 12^2 - 8^2)`
= 160 J [1]
b. PE gained = `4g * 10sin30` (= 200) [1]
Total work done = 200 – 160 [1]
Total work done = 40 J [1]
`–4 g*sin30 = 4*a [1]`
a = -5 ms-2 [1]
`-10 = 8t *-1/2 * 5 * t^2 [1]`
t = 4.16 s [1]
Question 11
A car of mass 1500 kg is pulling a trailer of mass 750 kg up a straight hill of length 800 m inclined at an angle of sin−1 0.08 to the horizontal. The resistances to the motion of the car and trailer are 400 N and 200 N respectively. The car and trailer are connected by a light rigid tow-bar. The car and trailer have speed 30 m s−1 at the bottom of the hill and 20 m s−1 at the top of the hill.
a. Use an energy method to find the constant driving force as the car and trailer travel up the hill. [5]
After reaching the top of the hill the system consisting of the car and trailer travels along a straight level road. The driving force of the car’s engine is 2400 N and the resistances to motion are unchanged.
b. Find the acceleration of the system and the tension in the tow-bar. [4]
a. KE (final) = `1/2*1500*20^2 + 1/2*750*20^2 [1]`
KE (initial) = `1/2*1500*30^2 + 1/2*750*30^2`
PE gain = `2250*10*800*0.08 [1]`
WD against friction = `600*800 [1]`
`1/2*2250*30^2 + DE*800 = 600*800 + 1/2*2250*20^2 + 2250*10*800*0.08 [1]`
DF = 1700 N [1]
`b. 2400 – 600 = 2250 * a [1]`
T – 200 = 750 a [1]
`T = 800 N and a = 0.8 ms^-2 [2]`
Question 12

Two particles A and B, of masses 0.3 kg and 0.5 kg respectively, are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley which is attached to a horizontal plane and to the top of an inclined plane. The particles are initially at rest with A on the horizontal plane and B on the inclined plane, which makes an angle of 30o with the horizontal. The string is taut and B can move on a line of greatest slope of the inclined plane. A force of magnitude 3.5 N is applied to B acting down the plane (see diagram).
a. Given that both planes are smooth, ϐind the tension in the string and the acceleration of B. [5]
b. It is given instead that the two planes are rough. When each particle has moved a distance of 0.6 m from rest, the total amount of work done against friction is 1.1 J. Use an energy method to ϐind the speed of B when it has moved this distance down the plane. [You should assume that the string is sufficiently long so that A does not hit the pulley when it moves 0.6 m. [4]
a. Applying Newton’s Second Law for both particle A and B
For A: T = 0.3 x a [1]
For B: 3.5 + 0.5 g sin 30 – T = 0.5 `*` a [1]
System: `3.5 + 0.5 g sin 30 = (0.3 + 0.5) * a [1]`
Solve that: a = = 7.5 ms-2 and T = 2.25 N [2]
b. PE loss by B
`PE = 0.5 g sin 30 * 0.6 = 1.5 J [1]`
`0.5 g sin 30 * 0.6 + 3.5 * 0.6 =` `1/2*0.8 *v^2 + 1.1.[1]`
v = 2.5 ms-1 [1]
Question 13
A box of mass 5 kg is pulled at a constant speed a distance of 15 m up a rough plane inclined at an angle of 20o to the horizontal. The box moves along a line of greatest slope against a frictional force of 40 N.
The force pulling the box is parallel to the line of greatest slope.
a. Find the work done against friction. [1]
b. Find the change in gravitational potential energy of the box. [2]
c. Find the work done by the pulling force. [1]
a. WD = 40 `*` 158 = 600 J [1]
b. Attempt PE gain
`PE = 5 * 10 * 15 sin 20 [1]`
= 257 J [1]
`c. WD = 40 * 15 + 5 * 10 × 15 sin 20 = 857 J [1]`
Question 14
A car of mass 1600 kg is pulling a caravan of mass 800 kg. The car and the caravan are connected by a light rigid tow-bar. The resistances to the motion of the car and caravan are 400 N and 250 N respectively.
a. The car and caravan are travelling along a straight horizontal road.
i. Given that the car and caravan have a constant speed of 25 m s−1, find the power of the car’s engine. [2]
ii. The engine’s power is now suddenly increased to 39 kW. Find the instantaneous acceleration of the car and caravan and find the tension in the tow-bar. [5]
b.The car and caravan now travel up a straight hill, inclined at an angle of sin−1 0.05 to the horizontal, at a constant speed of v m s−1 . The car’s engine is working at 32.5 kW. Find v. [3]
a. i. Use P = Fv with F = total resistance [1]
`P = 650 * 25 = 16 250 W [1]`
ii. DF = `39000/25`= 1560 [1]
For applying Newton’s 2nd law to the system to form an equation in a, or to the caravan or the car to form an equation in T and a
`1560 – 650 = 2400 * a [1]`
`T – 250 = 800 * a`
`1560 – 400 – T = 1600 * a [1]`
`a = frac(1560-650)(2400)`
`a = 0.379ms^-2 [1]`
T = 553N [1]
`b. DF = 650 + 2400 × 10 * 0.05 [1]`
`32 500 = (650 + 24 000 × 0.05) * v [1]`
`v = 17.6 ms^-1 [1]`
Question 15
A car of mass 1500 kg is pulling a trailer of mass 300 kg along a straight horizontal road at a constant speed of 20 m s−1. The system of the car and trailer is modelled as two particles, connected by a light rigid horizontal rod. The power of the car’s engine is 6000 W. There are constant resistances to motion of R N on the car and 80 N on the trailer.
a. Find the value of R. [2]
The power of the car’s engine is increased to 12 500 W. The resistance forces do not change.
b. Find the acceleration of the car and trailer and the tension in the rod at an instant when the speed of the car is 25 m s−1. [5]
a. Using F = `P/v`
Driving force = `6000/20`
= 300 N [1]
R = 300 – 80 = 220 N [1]
b. New driving force DF =`12500/25` = 500 N
`Car: DF – T – R = 1500 * a [1]`
`Trai l er: T – 80 = 300 * a [1]`
`System: DF – 80 – R = 1800 * a [1]`
`= 0.111 ms^-2 [1]`
T = 113N [1]
Question 16

The diagram shows the vertical cross-section PQR of a slide. The part PQ is a straight line of length 8 m inclined at angle `alpha` to the horizontal, where sin`alpha`= 0.8. The straight part PQ is tangential to the curved part QR, and R is h m above the level of P. The straight part PQ of the slide is rough and the curved part QR is smooth. A particle of mass 0.25 kg is projected with speed 15 m s−1 from P towards Q and comes to rest at R. The coefficient of friction between the particle and PQ is 0.5.
a. Find the work done by the friction force during the motion of the particle from P to Q. [4]
b. Hence find the speed of the particle at Q. [4]
c. Find the value of h. [3]
a. `R = 0.25 g * 0.6 = 1.5 [1]`
`F = 0.5 * 0.25 g * 0.6 = 0.75N [1]`
[WD against friction = F `*` 8] [1]
WD = 6 J [1]
b. `Work-energy equation in the form Initial KE = Final KE + WD against F + PE gain [1`
`1/2*0.25*152 = 1/2*0.25*v^2 + 6 + 0.25g*8*0.8 [1]`
v = 7 ms-2 [1]
c. `[1/2 * 0.25 * 72 = 0.25 * g * H] Or [1/2 * m * 72 = m * g * H] [1]`
`H = frac(7^2)(2*g) = 2.45 m [1]`
Total height h = 6.4 + H = 8.85 m [1]
Question 17
A lorry has mass 12 000 kg.
a. The lorry moves at a constant speed of 5 m s−1 up a hill inclined at an angle of `theta`o to the horizontal, where sin-1 = 0.08. At this speed, the magnitude of the resistance to motion on the lorry is 1500 N. Show that the power of the lorry’s engine is 55.5 kW. [3]
When the speed of the lorry is v m s−1 the magnitude of the resistance to motion is kv2 N, where k is a constant.
b. Show that k = 60. [1]
c. The lorry now moves at a constant speed on a straight level road. Given that its engine is still working at 55.5 kW, find the lorry’s speed. [3]
a. Using DF = Resistance + weight component
`DF = 1500 + 12 000 * g * 0.08 [DF = 11100] [1]`
Using P = Fv
`Power = DF * 5 [1]`
`Power = 11 100 * 5 = 55.5 kW [1]`
b. `k * 52 = 1500, k = 60 [1]`
c. Using DF = resistance = 60 v2
`DF = 60 v^2 [1]`
`55500 = DF * v = 60 v^2 * v = 60 v^3 [1]`
`v = 9.74 ms^-1 [1]`
Question 18
A particle of mass 1.3 kg rests on a rough plane inclined at an angle `theta`o to the horizontal, where tan`alpha = 12/5`. The coefficient of friction between the particle and the plane is `mu`.
a. A force of magnitude 20 N parallel to a line of greatest slope of the plane is applied to the particle and the particle is on the point of moving up the plane.
Show that `mu` = 1.6. [4]
b. The force of magnitude 20 N is now removed.
Find the acceleration of the particle. [2]
c. Find the work done against friction during the first 2 s of motion. [3]
a. R = 13 cos 67.4 = `13(5/13) [R = 5] [1]`
F + 13 sin 67.4 = F + `13(12/13) = 20 [F = 8] [1]`
`mu = 8/5 = 1.6 [1]`
b. `13 sin 67.4 – F = 1.3*a*F = muR = 8`
`to [4 = 1.3 a] [1]`
a = 3.08 ms-2 [1]
c. Use `s=ut +1/2 at^2` with `u=0` and a `≠ pm g` to find the distance moved in the first 2 seconds. [1]
s = 0 + 0.5`*(40/13) *2^2 [= 80/13 = 6.15] [1]`
WD = F × d [1]
`D = 8 * 6.15
WD = 49.2 J [1]`
Question 19

Two particles A and B, of masses 0.4 kg and 0.2 kg respectively, are connected by a light inextensible string. Particle A is held on a smooth plane inclined at an angle of `theta`o to the horizontal. The string passes over a small smooth pulley P fixed at the top of the plane, and B hangs freely 0.5 m above horizontal ground (see diagram). The particles are released from rest with both sections of the string taut.
a. Given that the system is in equilibrium, find `theta`. [3]
b. It is given instead that `theta` = 20. In the subsequent motion particle A does not reach P and B remains at rest after reaching the ground.
i. Find the tension in the string and the acceleration of the system. [4]
ii. Find the speed of A at the instant B reaches the ground. [2]
iii. Use an energy method to ϐind the total distance A moves up the plane before coming to instantaneous rest. [5]
a. Particle A: T = 4 sin`theta` [1]
Particle B: T = 2 [1]
`theta = 30 [1]`
b.
i. `A: T – 4 sin 20 = 0.4 a [1`
B: 2 – T = 0.2 a [1]
System: 2 – 4 sin 20 = (0.4 + 0.2) a [1]
T = 1.79 and a = 1.05 ms-2 [1]
ii. ``v^2 = 2 * 1.053 * 0.5 = 1.053 [1]`
v = 1.03 ms-1 [1]
iii. `Loss in KE = `1/2 * 0.4 * 1.053 = 0.2106 J [1]`
Gain in PE = `0.4 * 10 * d sin 20 [1]`
Apply KE loss = PE gain [1]
`1/2*0.4*1.053 = 0.3 * 10*d*sin20 [1]`
Total dist A moves up plane = 0.5 + d = 0.654 m [1]
Question 20
A car has mass 1000 kg. When the car is travelling at a steady speed of vm s−1, where v > 2, the resistance to motion of the car is (Av + B) N, where A and B are constants.
The car can travel along a horizontal road at a steady speed of 18 m s−1 when its engine is working at 36 kW.
The car can travel up a hill inclined at an angle of 1 to the horizontal, where sin-1 = 0.05, at a steady speed of 12 m s−1 when its engine is working at 21 kW.
Find A and B. [7].
Case 1: DF = `36000/18 [1]`
or Case 2: DF = `21000/12`
18 A + B = DF [`36000/18 = 18A + B = 2000] [1]`
18 A + B = 2000 [1]
12A + B = DF + weight component [`21000/12 = 12 A + B + 1000g *1/20] [1]`
12A + B = 1250 [1]
A = 125, B = –250 [2]
Question 1
A vase is pushed 1.6 m across a horizontal table by a horizontal force of 8N.
a. Find the work done by the force in pushing the vase [1]
b. Find the work done if the force acts at an angle of 30o to horizontal instead. [1]a. Work done is given by the formula Wd = F.d WD = 8 x 1.6 = 12.8 J [1] b. Applying the formula for work done by against a force acting at an angle of ? is Work done (WD) = Fdcos ? WD = 8 x 1.6 cos30 = 11.1 J [1]
Question 2
A package of mass 23kg is pulled 5m at a constant speed across a rough horizontal floor in an airport by a cord at an angle of sin-1(`7/25` ) above the horizontal. Given that the work done against friction is 240J.
Find the coefficient of friction between the package and the floor. [5]
Question 3
A cart of mass 8 kg is pushed 15 m up a rough plane inclined at an angle of 14o. The coefficient of friction between the cart and the plane `1/16`.
Find the total work done. [4]
Question 4
The intial velocity of buggy of mass 25 kg is 28ms-1.
Find the change in kinetic energy of the buggy after it decelerates at 1.6 ms-1 for 5s, stating whether it is an increase or a decrease.
Question 5
A flowerpot of mass 800g falls from a shelf 240 cm above the ground.
Find the loss of potential energy of the flowerpot.
Question 6
A rocket of mass 3kg is launched from the ground at 32 ms-1 and travels vertically.
Find the maximum height reached by the rocket by using:
a. The equation of uniformly accelerated motion
b. The change in energy
Question 7
A car of mass 1800 kg is towing a trailer of mass 400kg along a straight horizontal road. The car and trailer are connected by a light rigid tow-bar. The car is accelerating at 1.5 ms-2. There are constant resistance forces of 250N on the car and 100N on the trailer.
a. Find the tension in the tow-bar. [2]
b. Find the power of the engine of the car at the instant when the speed is 20 ms-1. [3]
Question 8
A child of mass 35 kg is swinging on a rope. The child is modelled as a particle P and the rope if modeled as a light inextensible string of length 4m. Initially P is held at an angle of 45o to the vertical (see diagram).
a. Given that there is no resistance force, find the speed of P when it has traveled halfway along the circular arc from its initial position to its lowest point [4].
b. It is given instead that there is a resistance force. The work done against the resistance force as P travels from its initial position to its lowest point is X J. The speed of P at its lowest point is 4 ms-1.
Find X [3].
Question 9
A car of mass 1250 kg is moving on a straight road. On a horizontal section of the road, the car has a constant speed of 32 ms−1 and there is a constant force of 750 N resisting the motion.
a. Calculate, in kW, the power developed by the engine of the car. [2]
i. Given that this power is suddenly decreased by 8 kW, find the instantaneous deceleration of the car. [3]
ii. On a section of the road inclined at sin−10.096 to the horizontal, the resistance to the motion of the car is (1000 + 8v) N when the speed of the car is v m s−1. The car travels up this section of the road at constant speed with the engine working at 60 kW.
Find this constant speed. [5]
Question 10
A block B of mass 4 kg is pushed up a line of greatest slope of a smooth plane inclined at 30o to
the horizontal by a force applied to B, acting in the direction of motion of B. The block passes through points P and Q with speeds 12 ms−1 and 8 ms−1 respectively. P and Q are 10 m apart with P below the level of Q.
a. Find the decrease in kinetic energy of the block as it moves from P to Q [2]
b. Hence find the work done by the force pushing the block up the slope as the block moves from P to Q. [3]
c. At the instant the block reaches Q, the force pushing the block up the slope is removed. Find the time taken, after this instant, for the block to return to P. [4]
Question 11
A car of mass 1500 kg is pulling a trailer of mass 750 kg up a straight hill of length 800 m inclined at an angle of sin−1 0.08 to the horizontal. The resistances to the motion of the car and trailer are 400 N and 200 N respectively. The car and trailer are connected by a light rigid tow-bar. The car and trailer have speed 30 m s−1 at the bottom of the hill and 20 m s−1 at the top of the hill.
a. Use an energy method to find the constant driving force as the car and trailer travel up the hill. [5]
After reaching the top of the hill the system consisting of the car and trailer travels along a straight level road. The driving force of the car’s engine is 2400 N and the resistances to motion are unchanged.
b. Find the acceleration of the system and the tension in the tow-bar. [4]
Question 12

Two particles A and B, of masses 0.3 kg and 0.5 kg respectively, are attached to the ends of a light inextensible string. The string passes over a fixed smooth pulley which is attached to a horizontal plane and to the top of an inclined plane. The particles are initially at rest with A on the horizontal plane and B on the inclined plane, which makes an angle of 30o with the horizontal. The string is taut and B can move on a line of greatest slope of the inclined plane. A force of magnitude 3.5 N is applied to B acting down the plane (see diagram).
a. Given that both planes are smooth, ϐind the tension in the string and the acceleration of B. [5]
b. It is given instead that the two planes are rough. When each particle has moved a distance of 0.6 m from rest, the total amount of work done against friction is 1.1 J. Use an energy method to ϐind the speed of B when it has moved this distance down the plane. [You should assume that the string is sufficiently long so that A does not hit the pulley when it moves 0.6 m. [4]
Question 13
A box of mass 5 kg is pulled at a constant speed a distance of 15 m up a rough plane inclined at an angle of 20o to the horizontal. The box moves along a line of greatest slope against a frictional force of 40 N.
The force pulling the box is parallel to the line of greatest slope.
a. Find the work done against friction. [1]
b. Find the change in gravitational potential energy of the box. [2]
c. Find the work done by the pulling force. [1]
Question 14
A car of mass 1600 kg is pulling a caravan of mass 800 kg. The car and the caravan are connected by a light rigid tow-bar. The resistances to the motion of the car and caravan are 400 N and 250 N respectively.
a. The car and caravan are travelling along a straight horizontal road.
i. Given that the car and caravan have a constant speed of 25 m s−1, find the power of the car’s engine. [2]
ii. The engine’s power is now suddenly increased to 39 kW. Find the instantaneous acceleration of the car and caravan and find the tension in the tow-bar. [5]
b.The car and caravan now travel up a straight hill, inclined at an angle of sin−1 0.05 to the horizontal, at a constant speed of v m s−1 . The car’s engine is working at 32.5 kW. Find v. [3]
Question 15
A car of mass 1500 kg is pulling a trailer of mass 300 kg along a straight horizontal road at a constant speed of 20 m s−1. The system of the car and trailer is modelled as two particles, connected by a light rigid horizontal rod. The power of the car’s engine is 6000 W. There are constant resistances to motion of R N on the car and 80 N on the trailer.
a. Find the value of R. [2]
The power of the car’s engine is increased to 12 500 W. The resistance forces do not change.
b. Find the acceleration of the car and trailer and the tension in the rod at an instant when the speed of the car is 25 m s−1. [5]
Question 16

The diagram shows the vertical cross-section PQR of a slide. The part PQ is a straight line of length 8 m inclined at angle `alpha` to the horizontal, where sin`alpha`= 0.8. The straight part PQ is tangential to the curved part QR, and R is h m above the level of P. The straight part PQ of the slide is rough and the curved part QR is smooth. A particle of mass 0.25 kg is projected with speed 15 m s−1 from P towards Q and comes to rest at R. The coefficient of friction between the particle and PQ is 0.5.
a. Find the work done by the friction force during the motion of the particle from P to Q. [4]
b. Hence find the speed of the particle at Q. [4]
c. Find the value of h. [3]
Question 17
A lorry has mass 12 000 kg.
a. The lorry moves at a constant speed of 5 m s−1 up a hill inclined at an angle of `theta`o to the horizontal, where sin-1 = 0.08. At this speed, the magnitude of the resistance to motion on the lorry is 1500 N. Show that the power of the lorry’s engine is 55.5 kW. [3]
When the speed of the lorry is v m s−1 the magnitude of the resistance to motion is kv2 N, where k is a constant.
b. Show that k = 60. [1]
c. The lorry now moves at a constant speed on a straight level road. Given that its engine is still working at 55.5 kW, find the lorry’s speed. [3]
Question 18
A particle of mass 1.3 kg rests on a rough plane inclined at an angle `theta`o to the horizontal, where tan`alpha = 12/5`. The coefficient of friction between the particle and the plane is `mu`.
a. A force of magnitude 20 N parallel to a line of greatest slope of the plane is applied to the particle and the particle is on the point of moving up the plane.
Show that `mu` = 1.6. [4]
b. The force of magnitude 20 N is now removed.
Find the acceleration of the particle. [2]
c. Find the work done against friction during the first 2 s of motion. [3]
Question 19

Two particles A and B, of masses 0.4 kg and 0.2 kg respectively, are connected by a light inextensible string. Particle A is held on a smooth plane inclined at an angle of `theta`o to the horizontal. The string passes over a small smooth pulley P fixed at the top of the plane, and B hangs freely 0.5 m above horizontal ground (see diagram). The particles are released from rest with both sections of the string taut.
a. Given that the system is in equilibrium, find `theta`. [3]
b. It is given instead that `theta` = 20. In the subsequent motion particle A does not reach P and B remains at rest after reaching the ground.
i. Find the tension in the string and the acceleration of the system. [4]
ii. Find the speed of A at the instant B reaches the ground. [2]
iii. Use an energy method to ϐind the total distance A moves up the plane before coming to instantaneous rest. [5]
Question 20
A car has mass 1000 kg. When the car is travelling at a steady speed of vm s−1, where v > 2, the resistance to motion of the car is (Av + B) N, where A and B are constants.
The car can travel along a horizontal road at a steady speed of 18 m s−1 when its engine is working at 36 kW.
The car can travel up a hill inclined at an angle of 1 to the horizontal, where sin-1 = 0.05, at a steady speed of 12 m s−1 when its engine is working at 21 kW.
Find A and B. [7].