Question 1
In how many ways can the six letters A, B, C, D, E and F be arranged in a row?
Easy
Mark as Complete
Mark Scheme
Question 2
From a standard deck of 52 playing cards, find how many ways there are of arranging in a row:
a. all 52 cards
b. the four kings
c. the 13 diamonds.
Easy
Mark as Complete
Mark Scheme
Question 3
Three identical cans of cola, 2 identical cans of green tea and 2 identical cans of orange juice are arranged in a row.
Calculate the number of arrangements if
a. the first and last cans in the row are the same type of drink, [3]
b. the 3 cans of cola are all next to each other and the 2 cans of green tea are not next to each other. [5]
Hard
Mark as Complete
Mark Scheme
Question 4
A group of n boys can be arranged in a line in a certain number of ways. By adding two more boys to the group, the number of possible arrangements increases by a factor of 420.
Find the value of n.
Easy
Mark as Complete
Mark Scheme
Question 5
Find the number of distinct arrangements of all the letters in these words:
a. TABLE
b. TABLET
c. COMMITTEE
d. MISSISSIPPI
e. HULLABALLOO
Easy
Mark as Complete
Mark Scheme
Question 6
A girl has 20 plastic squares. There are five identical red squares, seven identical blue squares and eight identical green squares. By placing them in a row, joined edge-to-edge, find how many different arrangements she can make using:
a. one square of each colour
b. the five red squares only
c. all of the blue and green squares
d. all of the 20 squares.
Easy
Mark as Complete
Mark Scheme
Question 7
Find how many ways four men and two women can stand in a line if:
a. the two women must be at the front
b. there must be a woman at the front and a man at the back
c. the two women must be separated
d. the four men must not be separated
e. no two men may stand next to each other
Easy
Mark as Complete
Mark Scheme
Question 8
From a group of 10 boys and seven girls, two are to be chosen to act as the hero and the villain in the school play. Find in how many ways this can be done if these two roles are to be played by:
a. any of the children
b. two girls or two boys
c. a boy and a girl.
Easy
Mark as Complete
Mark Scheme
Question 9
From seven men and eight women, find how many ways there are to select:
a. four men and five women
b. three men and six women
c. at least 13 people.
Easy
Mark as Complete
Mark Scheme
Question 10
Ten cars are to be parked in a car park that has 20 parking spaces set out in two rows of 10. Find how many different patterns of unoccupied parking spaces are possible if:
a. the cars can be parked in any of the 20 spaces
b. the cars are parked in the same row
c. the same number of cars are parked in each row
d. two more cars are parked in one row than in the other.
Easy
Mark as Complete
Mark Scheme
Question 11
From three sets of twins and four unrelated girls, find how many selections of five people can be made if exactly:
a. two sets of twins must be included
b. one set of twins must be included.
Easy
Mark as Complete
Mark Scheme
Question 12
Four bananas are randomly selected from a crate of 17 yellow and 23 green bananas. Find the probability that:
a. no green bananas are selected
b. less than half of those selected are green.
Easy
Mark as Complete
Mark Scheme
Question 13
A gardener has nine rose bushes to plant: three have red flowers and six have yellow flowers. If they plant them in a row in random order, find the probability that:
a. a yellow rose bush is in the middle of the row
b. the three red rose bushes are not separated
c. no two red rose bushes are next to each other.
Easy
Mark as Complete
Mark Scheme
Question 14
The 11 letters of the word REMEMBRANCE are arranged in a line.
a. Find the number of different arrangements if there are no restrictions. [1]
b. Find the number of different arrangements which start and finish with the letter M. [2]
c. Find the number of different arrangements which do not have all 4 vowels (E, E, A, E) next to each other. [3]
4 letters from the letters of the word REMEMBRANCE are chosen.
d. Find the number of different selections which contain no Ms and no Rs and at least 2 Es. [3]
Medium
Mark as Complete
Mark Scheme
Question 15
A bakery wishes to display seven of its 14 types of cake in a row in its shop window. There are six types of sponge cake, five types of cheesecake and three types of fruitcake. Find the number of possible displays that can be made if the bakery places:
a. a sponge cake at each end of the row and includes no fruitcakes in the display [2]
b. a fruitcake at one end of the row with sponge cakes and cheesecakes placed alternately in the remainder of the row. [4]
Medium
Mark as Complete
Mark Scheme
Question 16
Five cards, each marked with a different single-digit number from 3 to 7, are randomly placed in a row. Find the probability that the first card in the row is odd and that the three cards in the middle of the row have a sum of 15.
Medium
Mark as Complete
Mark Scheme
Question 17
Three ordinary fair dice are rolled. Find the number of ways in which the number rolled with the first die can exceed the sum of the numbers rolled with the second and third dice. Hence, find the probability that this event does not occur in two successive rolls of the three dice.
Hard
Mark as Complete
Mark Scheme
Question 18
Two ordinary fair dice are rolled and the two faces on which they come to rest are hidden by holding the dice together, as shown, and lifted off the table.
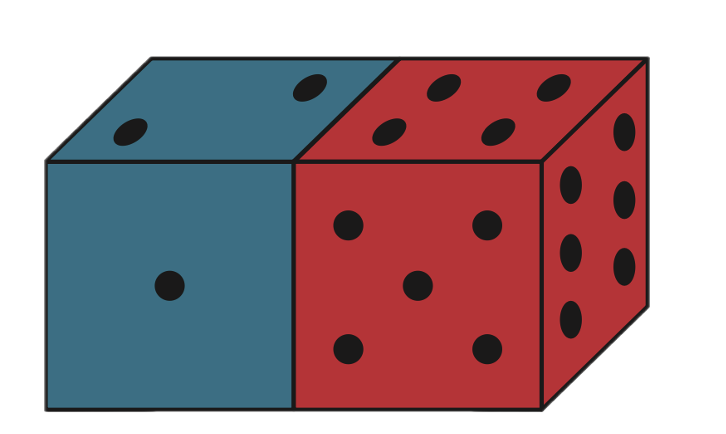
The sum of the numbers on the 10 visible faces of the dice is denoted by T.
a Find the number of possible values of T, and find the most likely value of T. [4]
b Calculate the probability that T ≤ 38
Hard
Mark as Complete
Mark Scheme
Question 19
How many even four-digit numbers can be made from the digits 0, 2, 3, 4, 5 and 7, each used at most once, when the first digit cannot be zero?
Hard
Mark as Complete
Mark Scheme
Question 20
a.
i. Find how many numbers there are between 100 and 999 in which all three digits are different. [3]
ii. Find how many of the numbers in part i are odd numbers greater than 700. [4]
b. A bunch of flowers consists of a mixture of roses, tulips and daffodils. Tom orders a bunch of 7 flowers from a shop to give to a friend. There must be at least 2 of each type of flower. The shop has 6 roses, 5 tulips and 4 daffodils, all different from each other.
Find the number of different bunches of flowers that are possible. [4]
Hard
Mark as Complete
Mark Scheme
Question 1
In how many ways can the six letters A, B, C, D, E and F be arranged in a row?
Arrange six from six letters:
`P_6^6 = 6! = 6*5*4*3*2*1 = 720`
Question 2
From a standard deck of 52 playing cards, find how many ways there are of arranging in a row:
a. all 52 cards
b. the four kings
c. the 13 diamonds.
a. Arrange 52 from 52 cards
`P_52^52 = 52! = 52*51*50.... 3×2×1=8.07×10^67`
b. Arrange four from four cards
`P_4^4 = 4! = 4*3*2*1=24`
c. Arrange 13 from 13 cards
`P_13^13 = 13! = 13*12*11 … 2×1=6227020800`
Question 3
Three identical cans of cola, 2 identical cans of green tea and 2 identical cans of orange juice are arranged in a row.
Calculate the number of arrangements if
a. the first and last cans in the row are the same type of drink, [3]
b. the 3 cans of cola are all next to each other and the 2 cans of green tea are not next to each other. [5]
a. There are `frac(5!)(2!*2!)`distinct arrangements between two colas
There are `frac(5!)(3!*2!)`distinct arrangements between two green teas
There are `frac(5!)(3!*2!)`distinct arrangements between two orange juices
Total is `frac(5!)(2!*2!) + frac(5!)(3!*2!) + frac(5!)(3!*2!) = 50`
b. Arrange the block of three colas with the two orange juices: `frac(3!)(2!) = 3`
Select two of the four spaces between or on either side of these in which to put the two cans of green tea (no arranging needed as they are identical): `C_4^2`'
Total is `3*C_4^2 = 18`
Question 4
A group of n boys can be arranged in a line in a certain number of ways. By adding two more boys to the group, the number of possible arrangements increases by a factor of 420.
Find the value of n.
`frac((n+2)!)(n) = (n +2)(n+1) = 420`
`n^2+3n -418=0`
`(n+22)(n-19)=0`so n = 19
Question 5
Find the number of distinct arrangements of all the letters in these words:
a. TABLE
b. TABLET
c. COMMITTEE
d. MISSISSIPPI
e. HULLABALLOO
a. Five letters with no repeats 5! = 120
b. Six letters with two Ts: `frac(6!)(2!) = 360`
c. Nine letters with two Ms, two Ts and two Es: `frac(9!)(2! * 2!*2!) = 45360`
d. Eleven letters with four Is, four Ss and two Ps: `frac(11!)(4! *4!*2!) = 34650`
e. Eleven letters with four Ls, two As, and two Os: `frac(11!)(4! *2!*2!) = 415 800`
Question 6
A girl has 20 plastic squares. There are five identical red squares, seven identical blue squares and eight identical green squares. By placing them in a row, joined edge-to-edge, find how many different arrangements she can make using:
a. one square of each colour
b. the five red squares only
c. all of the blue and green squares
d. all of the 20 squares.
a. Three squares with non identical:`P_6^6 =3! =6`
b. Five squares with five identical in shape and color: `frac(5!)(5!) = 1`
c. Fifteen squares with seven identical blue and eight identical green: `frac(15!)(7! * 8!) = 6435`
d. Twenty squares with five identical red, seven identical blue and eight identical green: `frac(20!)(5!*7!*8!) = 99768240`
Question 7
Find how many ways four men and two women can stand in a line if:
a. the two women must be at the front
b. there must be a woman at the front and a man at the back
c. the two women must be separated
d. the four men must not be separated
e. no two men may stand next to each other
a. The two women can be at the front in `P_2^2` ways, and the four men can be arranged behind them in `P_4^4`ways.
Total is `P_2^2 * P_4^4 = 48`
b. A woman can be placed at the front in `P_2^1` ways, and a man can be placed at the back in `P_4^1` ways. The other four people can be arranged between them in `P_4^4` ways.
Total is `P_2^1 * P_4^1 * P_4^4`=192
c. We can find the number of arrangements in which the two women are not separated then subtract this from the total number of possible arrangements of six people.
Total number of possible arrangements of six people is `P_6^6`.
The two women can be next to each other in `P_2^2`, ways.
The block of two women can be arranged with the four men in `P_5^5`ways.
Total is `P_6^6 -(P _2^2*P_5^5 )=480`
d The four men can be arranged in `P_4 ^4`ways. This block of four men can be arranged with the two women in `P_3^3`ways.
Total is `P_4^4*P_3^3 =480`
e None. There are only three spaces between or on either side of the two women, so the four men cannot all be separated
Question 8
From a group of 10 boys and seven girls, two are to be chosen to act as the hero and the villain in the school play. Find in how many ways this can be done if these two roles are to be played by:
a. any of the children
b. two girls or two boys
c. a boy and a girl.
a. Select two from 17 children and arrange as hero and villain: `P_17^2 =272`
b. Select and arrange two from seven girls or two from ten boys: `P_7^2 + P_10^2 =132`
c. 272-132=140
Question 9
From seven men and eight women, find how many ways there are to select:
a. four men and five women
b. three men and six women
c. at least 13 people.
a. Select four from seven men, and five from eight women: `C_7^4*C_8^5 =1960`
b. Select three from seven men, and six from eight women: `C_7 ^3 *C_8^6 =980`
c. Select 13 or 14 or 15 people from 15 people:`C_15^13*C_15^14 +C_15^15 = 121`
Question 10
Ten cars are to be parked in a car park that has 20 parking spaces set out in two rows of 10. Find how many different patterns of unoccupied parking spaces are possible if:
a. the cars can be parked in any of the 20 spaces
b. the cars are parked in the same row
c. the same number of cars are parked in each row
d. two more cars are parked in one row than in the other.
a. Select ten of the 20 spaces to leave empty: `C_20^10` =184756
b. 1st row empty and 2nd row full or 1st row full and 2nd row empty: two arrangements
c. Select six spaces to leave empty in each row: `C_10^5 *C_10^5`=63504
d. Select six spaces to leave empty in the 1st row, and four spaces to leave empty in the 2nd row, or vice versa. Total is `(C_10^6 *C_10^4 )+(C_10^4 *C_10^6 )=88200`
Question 11
From three sets of twins and four unrelated girls, find how many selections of five people can be made if exactly:
a. two sets of twins must be included
b. one set of twins must be included.
a. `C_3^2* C_6^1 =18`
b There are `C_3^1`ways to select one set of twins. For the other three people, there are three possibilities:
3 girls: `C_4^3`
or 1 twin and 2 girls: `C_4^1* C_4^2`
or 2 who are twins (but not each other’s twin) and 1 girl: `4*C_4^1`
Total is `C_3^1*[C_4^3 +(C_4^1* C_4^2) + (4*C_4^1)] =132`
Question 12
Four bananas are randomly selected from a crate of 17 yellow and 23 green bananas. Find the probability that:
a. no green bananas are selected
b. less than half of those selected are green.
a. Total number of possible selections: `C_40^4`
Favorable selections are four from 17 yellow and none from 23 green: `C_17^4 * C_23^0`
`frac(C_17^4 * C_23^0)(C_40^4) = 0.026`
b. Favorable selections are four from 17 yellow and none from 23 green, or three from 17 yellow and one from 23 green: `frac(C_17^4 * C_23^0)(C_40^4) + frac(C_17^3 * C_23^1)(C_40^4)` = 0.197
Question 13
A gardener has nine rose bushes to plant: three have red flowers and six have yellow flowers. If they plant them in a row in random order, find the probability that:
a. a yellow rose bush is in the middle of the row
b. the three red rose bushes are not separated
c. no two red rose bushes are next to each other.
a. The nine rose bushes are equally likely to be in the middle: `6/9 = 2/3`
b. Total number of arrangements: `P_9^9`
Arrangements of three red in a row: `P_3^3`
Arrangements of the block of three red with the six yellow: `P_7^7`
c. Arrange six yellow in a row: `P_6^6`
Select three of the seven spaces between or on either side of the yellow bushes: `P_7^3`
`frac(P_6^6 * P_7^3)(P_9^9) = 5/12`
Question 14
The 11 letters of the word REMEMBRANCE are arranged in a line.
a. Find the number of different arrangements if there are no restrictions. [1]
b. Find the number of different arrangements which start and finish with the letter M. [2]
c. Find the number of different arrangements which do not have all 4 vowels (E, E, A, E) next to each other. [3]
4 letters from the letters of the word REMEMBRANCE are chosen.
d. Find the number of different selections which contain no Ms and no Rs and at least 2 Es. [3]
a. Arrange 11 letters with two Rs, three Es and two Ms:
`frac(11!)(2!*3!*2!) = 1663200`
b. Arrange nine letters with two Rs and three Es: `frac(9!)(2!*3!) = 30240`
c. We subtract arrangements with the vowels net to each other from the 1663200 unrestricted arrangements. Four vowels next to each other: `(4!)/(3!`
Arrange the block of four vowels with the other seven letters (which includes two Ts and two Ms): `frac(8!)(2!*2!)`
16663200 - `(frac(4!)(3!) * frac(8!)(2!*2!)) = 1622880`
d. Favorable selections have two Es and two from BANC, or three Es and one from BANC: `C_4^2 * C_4^1 = 10`
Question 15
A bakery wishes to display seven of its 14 types of cake in a row in its shop window. There are six types of sponge cake, five types of cheesecake and three types of fruitcake. Find the number of possible displays that can be made if the bakery places:
a. a sponge cake at each end of the row and includes no fruitcakes in the display [2]
b. a fruitcake at one end of the row with sponge cakes and cheesecakes placed alternately in the remainder of the row. [4]
a. Sponge cake at each end: `P_6^2`
Select and arrange five of the remaining nine non-fruitcakes: `P_9^5`
Total is `P_6^2 * P_5^9 = 45600`
b. One of three fruitcakes `P_3^1` go at either and `P_2^1` of the row.
Three of six sponge cakes `P_6^3` and three of five cheesecakes `P_5^3`are placed alternately `P_2^1`
Total is `P_3^1 * P_2^1 * P_6^3 * P_5^3 * P_2^1` = 86400
Question 16
Five cards, each marked with a different single-digit number from 3 to 7, are randomly placed in a row. Find the probability that the first card in the row is odd and that the three cards in the middle of the row have a sum of 15.
Total number of possible arrangement: `P_5^5 = 120`
A sum of 15 can only be made with 4, 5 and 6, so the odd number is 3 or 7
Number of favorable arrangements is `2*P_3^3 * 1= 12`
Probability is `12/120 = 1/10`
Question 17
Three ordinary fair dice are rolled. Find the number of ways in which the number rolled with the first die can exceed the sum of the numbers rolled with the second and third dice. Hence, find the probability that this event does not occur in two successive rolls of the three dice.
1st die value is 1, 2, 3, 4, 5 or 6
2nd and 3rd dice sum is 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 or 12
| 1st > 2nd + 3rd | No. ways |
| 3>2 | 1 |
| 4>2 or 3 | 1+2=3 |
| 5>2,3 or 4 | 1+2+3=6 |
| 6>2,3,4 or 5 | 1+2+3+4=10 |
|
| Total = 20 |
There are 20 ways
P (event does not occur) = `20*(1/6)^3 = 20/216`
P(event does not occur twice in succession) = `( 1- 20/216)^2`
= `2401/2916` or 0.823
Question 18
Two ordinary fair dice are rolled and the two faces on which they come to rest are hidden by holding the dice together, as shown, and lifted off the table.

The sum of the numbers on the 10 visible faces of the dice is denoted by T.
a Find the number of possible values of T, and find the most likely value of T. [4]
b Calculate the probability that T ≤ 38
a. Sum of all twelve faces on two dice is 42
Sum of hidden numbers, S = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 or 12
T = 42 - S, so T = 30, 31, 32, 33, 34, 35, 36, 37, 38, 39 or 40
T has 11 possible values
The most likely value of S is 7, so the most likely value of T is 42 - 7 = 35
b. P `(T le 38) = 1 - P(S < 4) = 1 - [P(1,1) + P(1,2) + P(2,1)] = 1 - 3/36 = 11/12`
Question 19
How many even four-digit numbers can be made from the digits 0, 2, 3, 4, 5 and 7, each used at most once, when the first digit cannot be zero?
Ends in 0: `P_5^3 = 60`
End in 2 or 4: `4*P_4^2 * 2 = 96`
Total is 60 + 96 = 156
Question 20
a.
i. Find how many numbers there are between 100 and 999 in which all three digits are different. [3]
ii. Find how many of the numbers in part i are odd numbers greater than 700. [4]
b. A bunch of flowers consists of a mixture of roses, tulips and daffodils. Tom orders a bunch of 7 flowers from a shop to give to a friend. There must be at least 2 of each type of flower. The shop has 6 roses, 5 tulips and 4 daffodils, all different from each other.
Find the number of different bunches of flowers that are possible. [4]
a
i. `9*9*8 = 648`
ii. Numbers beginning with 7: `1*C_8^1 * C_4^1 = 32`
Numbers beginning with 8: `1*C_8^1*C_5^1 = 40`
Numbers beginning with 9: `1*C_8^1 * C_4^1 = 32`
Total is 32 + 40 + 32 = 104
b.
| 2R | 2T | 3D | `C_6^2 * C_5^2 * C_4^3 = 600` |
| 2R | 3T | 2D | `C_6^2 * C_5^3 * C_4^2 = 900` |
| 3R | 2T | 2D | `C_6^3 * C_5^2 * C_4^2 = 1200` |
Total is 2700
Question 1
In how many ways can the six letters A, B, C, D, E and F be arranged in a row?
Question 2
From a standard deck of 52 playing cards, find how many ways there are of arranging in a row:
a. all 52 cards
b. the four kings
c. the 13 diamonds.
Question 3
Three identical cans of cola, 2 identical cans of green tea and 2 identical cans of orange juice are arranged in a row.
Calculate the number of arrangements if
a. the first and last cans in the row are the same type of drink, [3]
b. the 3 cans of cola are all next to each other and the 2 cans of green tea are not next to each other. [5]
Question 4
A group of n boys can be arranged in a line in a certain number of ways. By adding two more boys to the group, the number of possible arrangements increases by a factor of 420.
Find the value of n.
Question 5
Find the number of distinct arrangements of all the letters in these words:
a. TABLE
b. TABLET
c. COMMITTEE
d. MISSISSIPPI
e. HULLABALLOO
Question 6
A girl has 20 plastic squares. There are five identical red squares, seven identical blue squares and eight identical green squares. By placing them in a row, joined edge-to-edge, find how many different arrangements she can make using:
a. one square of each colour
b. the five red squares only
c. all of the blue and green squares
d. all of the 20 squares.
Question 7
Find how many ways four men and two women can stand in a line if:
a. the two women must be at the front
b. there must be a woman at the front and a man at the back
c. the two women must be separated
d. the four men must not be separated
e. no two men may stand next to each other
Question 8
From a group of 10 boys and seven girls, two are to be chosen to act as the hero and the villain in the school play. Find in how many ways this can be done if these two roles are to be played by:
a. any of the children
b. two girls or two boys
c. a boy and a girl.
Question 9
From seven men and eight women, find how many ways there are to select:
a. four men and five women
b. three men and six women
c. at least 13 people.
Question 10
Ten cars are to be parked in a car park that has 20 parking spaces set out in two rows of 10. Find how many different patterns of unoccupied parking spaces are possible if:
a. the cars can be parked in any of the 20 spaces
b. the cars are parked in the same row
c. the same number of cars are parked in each row
d. two more cars are parked in one row than in the other.
Question 11
From three sets of twins and four unrelated girls, find how many selections of five people can be made if exactly:
a. two sets of twins must be included
b. one set of twins must be included.
Question 12
Four bananas are randomly selected from a crate of 17 yellow and 23 green bananas. Find the probability that:
a. no green bananas are selected
b. less than half of those selected are green.
Question 13
A gardener has nine rose bushes to plant: three have red flowers and six have yellow flowers. If they plant them in a row in random order, find the probability that:
a. a yellow rose bush is in the middle of the row
b. the three red rose bushes are not separated
c. no two red rose bushes are next to each other.
Question 14
The 11 letters of the word REMEMBRANCE are arranged in a line.
a. Find the number of different arrangements if there are no restrictions. [1]
b. Find the number of different arrangements which start and finish with the letter M. [2]
c. Find the number of different arrangements which do not have all 4 vowels (E, E, A, E) next to each other. [3]
4 letters from the letters of the word REMEMBRANCE are chosen.
d. Find the number of different selections which contain no Ms and no Rs and at least 2 Es. [3]
Question 15
A bakery wishes to display seven of its 14 types of cake in a row in its shop window. There are six types of sponge cake, five types of cheesecake and three types of fruitcake. Find the number of possible displays that can be made if the bakery places:
a. a sponge cake at each end of the row and includes no fruitcakes in the display [2]
b. a fruitcake at one end of the row with sponge cakes and cheesecakes placed alternately in the remainder of the row. [4]
Question 16
Five cards, each marked with a different single-digit number from 3 to 7, are randomly placed in a row. Find the probability that the first card in the row is odd and that the three cards in the middle of the row have a sum of 15.
Question 17
Three ordinary fair dice are rolled. Find the number of ways in which the number rolled with the first die can exceed the sum of the numbers rolled with the second and third dice. Hence, find the probability that this event does not occur in two successive rolls of the three dice.
Question 18
Two ordinary fair dice are rolled and the two faces on which they come to rest are hidden by holding the dice together, as shown, and lifted off the table.

The sum of the numbers on the 10 visible faces of the dice is denoted by T.
a Find the number of possible values of T, and find the most likely value of T. [4]
b Calculate the probability that T ≤ 38
Question 19
How many even four-digit numbers can be made from the digits 0, 2, 3, 4, 5 and 7, each used at most once, when the first digit cannot be zero?
Question 20
a.
i. Find how many numbers there are between 100 and 999 in which all three digits are different. [3]
ii. Find how many of the numbers in part i are odd numbers greater than 700. [4]
b. A bunch of flowers consists of a mixture of roses, tulips and daffodils. Tom orders a bunch of 7 flowers from a shop to give to a friend. There must be at least 2 of each type of flower. The shop has 6 roses, 5 tulips and 4 daffodils, all different from each other.
Find the number of different bunches of flowers that are possible. [4]