Question 1
United’s manager estimates that the team has a 65% chance of winning any particular game and an 85% chance of not drawing any particular game.
a. What are the manager’s estimates most likely to be based on?
b. If the team plays 40 games this season, find the manager’s expectation of the number of games the team will lose.
c. If the team loses one game more than the manager expects this season, explain why this does not necessarily mean that they performed below expectation.
Easy
Mark as Complete
Mark Scheme
Question 2
A numbered wheel is divided into eight sectors of equal size, as shown. The wheel is spun until it stops with the arrow pointing at one of the numbers. Axel decides to spin the wheel 400 times.
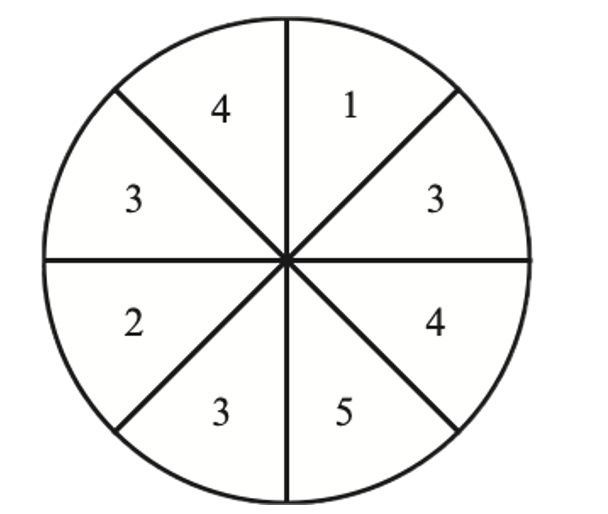
a. Find the number of times the arrow is not expected to point at a 4.
b. How many more times must Axel spin the wheel so that the expected number of times that the arrow points at a 4 is at least 160?
Easy
Mark as Complete
Mark Scheme
Question 3
In a group of 25 boys, nine are members of the chess club (C ), eight are members of the debating club (D) and 10 are members of neither of these clubs. This information is shown in the Venn diagram.
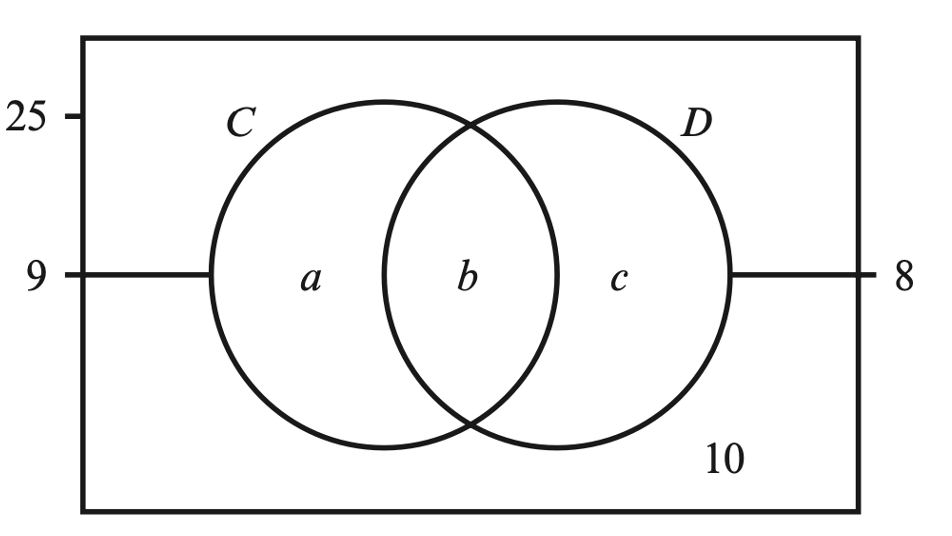
a. Find the values of a, b and c.
b. Find the probability that a randomly selected boy is:
i. a member of the chess club or the debating club
ii. a member of exactly one of these clubs.
Easy
Mark as Complete
Mark Scheme
Question 4
Forty girls were asked to name the capital of Cuba and of Hungary; 19 knew the capital of Cuba, 20 knew the capital of Hungary and seven knew both.
a. Draw a Venn diagram showing the number of girls who knew each of these capitals.
b. Find the probability that a randomly selected girl knew:
i. the capital of Cuba but not of Hungary
ii. just one of these capitals.
Easy
Mark as Complete
Mark Scheme
Question 5
A garage repaired 132 vehicles last month. The number of vehicles that required electrical (E), mechanical (M) and bodywork (B) repairs are given in the diagram opposite.
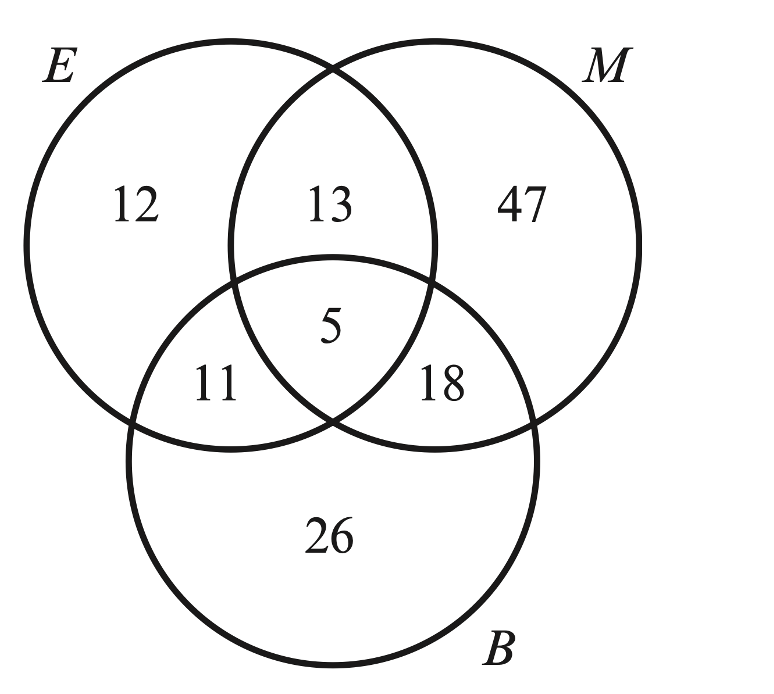
Find the probability that a randomly selected vehicle required:
a. mechanical or bodywork repairs
b. no bodywork repairs
c. exactly two types of repair.
Easy
Mark as Complete
Mark Scheme
Question 6
Events X and Y are such that P(X) = 0.5, P(Y) = 0.6 and P(`X cap Y)` = 0.2
a. State, giving a reason, whether events X and Y are mutually exclusive.
b. Using a Venn diagram, or otherwise, find `P(X capY)`.
c. Find the probability that X or Y, but not both, occurs.
Easy
Mark as Complete
Mark Scheme
Question 7
Each of 27 tourists was asked which of the countries Angola (A), Burundi (B) and Cameroon (C) they had visited. Of the group, 15 had visited Angola; 8 had visited Burundi; 12 had visited Cameroon; 2 had visited all three countries; and 21 had visited only one. Of those who had visited Angola, 4 had visited only one other country. Of those who had not visited Angola, 5 had visited Burundi only. All of the tourists had visited at least one of these countries.
a. Draw a fully labelled Venn diagram to illustrate this information.
b. Find the number of tourists in set B′ and describe them.
c. Describe the tourists in set `(A cup B) cap C'`and state how many there are.
d. Find the probability that a randomly selected tourist from this group had visited at least two of these three countries.
Easy
Mark as Complete
Mark Scheme
Question 8
The probabilities that a team wins, draws or loses any particular game are 0.6, 0.1 and 0.3, respectively.
a . Find the probability that the team wins at least one of its next two games.
b. If 2 points are awarded for a win, 1 point for a draw and 0 points for a loss, find the probability that the team scores a total of more than 1 point in its next two games.
Easy
Mark as Complete
Mark Scheme
Question 9
A biased die in the shape of a pyramid has five faces marked 1, 2, 3, 4 and 5. The possible scores are 1, 2, 3, 4 and 5 and `P(x) = frac(k-x)(25)`,
where k is a constant.
a. Find, in terms of k, the probability of scoring:
i. 5
ii. less than 3
b. The die is rolled three times and the scores are added together. Evaluate k and find the probability that the sum of the three scores is less than 5.
Easy
Mark as Complete
Mark Scheme
Question 10
A,B and C are independent events, and it is given that `P(A capB) = 0. 35, P(B cap C) = 0.56` and `P(A capC) = 0.4`
a. Express in terms of:
i. P(B)
ii. P(C)
b. Use your answers to part a to find:
i. P(B)
ii. P(A')
iii. `P(B' capC')`
Easy
Mark as Complete
Mark Scheme
Question 11
Two ordinary fair dice are rolled.
Event X is the product of the two numbers obtained is odd.
EventY is the sum of the two numbers obtained is a multiple of 3.
a. Determine, giving reasons for your answer, whether X and Y are independent.
b. Are events X and Y mutually exclusive? Justify your answer.
Easy
Mark as Complete
Mark Scheme
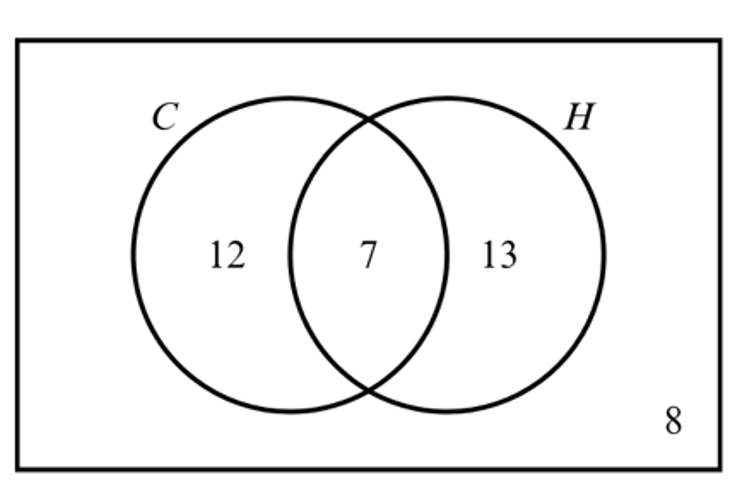
Question 12
One hundred children were each asked whether they have brothers (B) and whether they have sisters (S). Their responses are given in the Venn diagram.
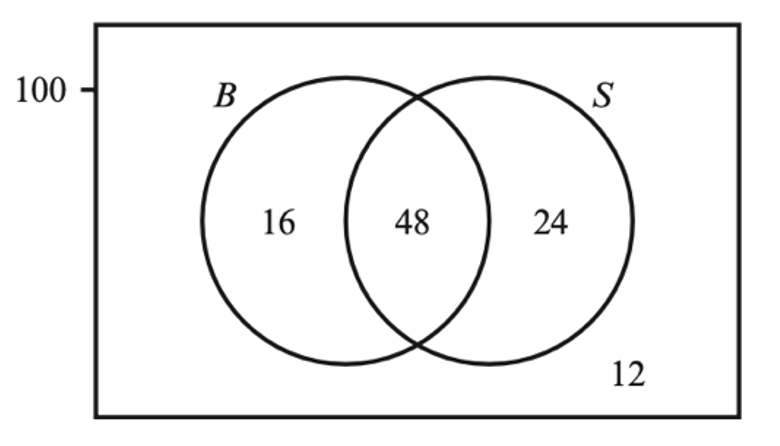
Find the probability that a randomly selected child has:
a. sisters, given that they have brothers
b. brothers, given that they do not have sisters
c. sisters or brothers, given that they do not have both.
Easy
Mark as Complete
Mark Scheme
Question 13
Anya calls Zara once each evening before she goes to bed. She calls Zara’s mobile phone with probability 0.8 or her landline. The probability that Zara answers her mobile phone is 0.74, and the probability that she answers her landline is y. This information is displayed in the tree diagram shown.
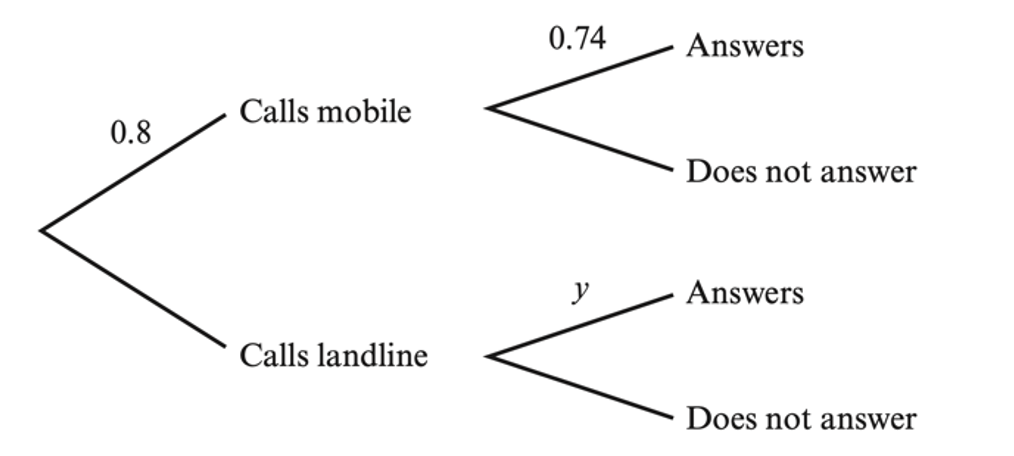
a. Given that Zara answers 68% of Anya’s calls, find the value of y.
b. Given that Anya’s call is not answered, find the probability that it is made to Zara’s landline.
Medium
Mark as Complete
Mark Scheme
Question 14
Every Friday, Arif offers to take his sons to the beach or to the park. The sons refuse an offer to the beach with probability 0.65 and accept an offer to the park with probability 0.85. The probability that Arif offers to take them to the beach is x. This information is shown in the tree diagram
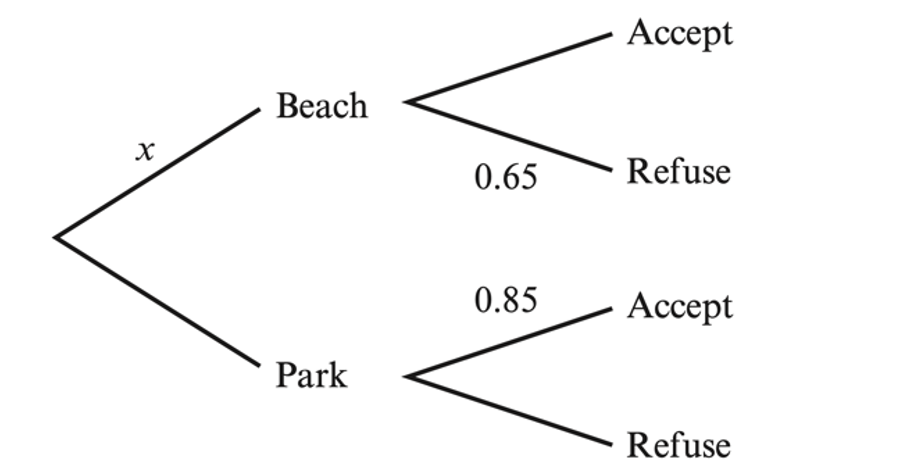
a. Find the value of x, given that 33% of Arif’s offers are refused
b. Given that Arif’s offer is accepted, find the probability that he offers to take his sons to the park
Medium
Mark as Complete
Mark Scheme
Question 15
Three friends, Rick, Brenda and Ali, go to a football match but forget to say which entrance to the ground they will meet at. There are four entrances, A, B, C and D. Each friend chooses an entrance independently.
a. Find the probability that at least 2 friends will choose entrance B.
b. Find the probability that the three friends will all choose the same entrance.
Medium
Mark as Complete
Mark Scheme
Question 16
Maria chooses toast for her breakfast with probability 0.85. If she does not choose toast then she has a bread roll. If she chooses toast then the probability that she will have jam on it is 0.8. If she has a bread roll then the probability that she will have jam on it is 0.4.
a. Draw a fully labelled tree diagram to show this information.
b. Given that Maria did not have jam for breakfast, find the probability that she had toast.
Hard
Mark as Complete
Mark Scheme
Question 17
Ronnie obtained data about the gross domestic product (GDP) and the birth rate for 170 countries. He classified each GDP and each birth rate as either ‘low’, ‘medium’ or ‘high’. The table shows the number of countries in each category.
|
| Birth rate | |||
| Low | Medium | High | ||
| GDP | Low | 3 | 5 | 45 |
| Medium | 20 | 42 | 12 | |
| High | 35 | 8 | 0 | |
One of these countries is chosen at random.
a. Find the probability that the country chosen has a medium GDP
b. Find the probability that the country chosen has a low birth rate, given that it does not have a
medium GDP
c. State with a reason whether or not the events ‘the country chosen has a high GDP’ and ‘the country chosen has a high birth rate’ are exclusive
One country is chosen at random from those countries which have a medium GDP and then a different country is chosen at random from those which have a medium birth rate.
d. Find the probability that both countries chosen have a medium GDP and a medium birth rate
Hard
Mark as Complete
Mark Scheme
Question 18
Two ordinary fair dice are rolled. Event A is ‘the sum of the numbers rolled is 2, 3 or 4’. Event B is ‘the absolute difference between the numbers rolled is 2, 3 or 4’.
a. When the dice are rolled, they show a 1 and a 3. Explain why this result shows that events A and B are not mutually exclusive.
b. Explain how you know that `P(A capB) = 1/18`
c. Determine whether events A and B are independent.
Hard
Mark as Complete
Mark Scheme
Question 19
Bookings made at a hotel include a room plus any meal combination of breakfast (B), lunch (L) and supper (S). The Venn diagram opposite shows the number of each type of booking made by 71 guests on Friday.
a. A guest who has not booked all three meals is selected at random.
Find the probability that this guest:
i. has booked breakfast or supper
ii. has not booked supper, given that they have booked lunch.
b. Find the probability that two randomly selected guests have both booked lunch, given that they have both booked at least two meals.
Hard
Mark as Complete
Mark Scheme
Question 20
The following table shows the numbers of IGCSE (I) and A Level (A) examinations passed by a group of university students.
|
| IGCSEs (I) | ||||||
| 5 | 6 | 7 | 8 | 9 | 10 | ||
| A Levels (A) | 2 | 13 | 9 | 5 | 4 | 2 | 0 |
| 3 | 7 | 8 | 9 | 6 | 1 | 0 | |
| 4 | 0 | 0 | 1 | 0 | 1 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | |
a. For a student selected at random, find:
i. P(A < 4)
ii. P(I + A > 10)
b. Six students who all have at least three A Level passes are selected at random.
Find the greatest possible range of the total number of IGCSE passes that they could have.
Hard
Mark as Complete
Mark Scheme
Question 1
United’s manager estimates that the team has a 65% chance of winning any particular game and an 85% chance of not drawing any particular game.
a. What are the manager’s estimates most likely to be based on?
b. If the team plays 40 games this season, find the manager’s expectation of the number of games the team will lose.
c. If the team loses one game more than the manager expects this season, explain why this does not necessarily mean that they performed below expectation.
a. From the team’s previous result
b `P_(lose) = 1 - [P_(w i n) + P_(draw)]`
`P_(lose) = 1 - [0.65 + (1 - 0.85)] = 0.2`
Expectation = `40*P_(lose) = 40 * 0.2`
Expectation = 8 games
c. They may win some of the games that they are expected to draw
Question 2
A numbered wheel is divided into eight sectors of equal size, as shown. The wheel is spun until it stops with the arrow pointing at one of the numbers. Axel decides to spin the wheel 400 times.

a. Find the number of times the arrow is not expected to point at a 4.
b. How many more times must Axel spin the wheel so that the expected number of times that the arrow points at a 4 is at least 160?
a. Expectation = `n*`P(not 4) = `400*6/8 = 300`
b. `(400 + x) * 2/8 ge 240,`so he must spin the wheel at least 240 more times.
Question 3
In a group of 25 boys, nine are members of the chess club (C ), eight are members of the debating club (D) and 10 are members of neither of these clubs. This information is shown in the Venn diagram.

a. Find the values of a, b and c.
b. Find the probability that a randomly selected boy is:
i. a member of the chess club or the debating club
ii. a member of exactly one of these clubs.
a. Solve
`a + b + c + 10 = 25a + b = 9b + c = 8`
`a = 7b = 2c = 6`
b. i. The events are not mutually exclusive:
`9/25 + 8/25 - 2/25 = 3/5`or `frac(7 + 2 + 6)(25) = 3/5`
ii. `frac(7 +6)(25) = 13/25`
Question 4
Forty girls were asked to name the capital of Cuba and of Hungary; 19 knew the capital of Cuba, 20 knew the capital of Hungary and seven knew both.
a. Draw a Venn diagram showing the number of girls who knew each of these capitals.
b. Find the probability that a randomly selected girl knew:
i. the capital of Cuba but not of Hungary
ii. just one of these capitals.
a.
b. i. `12/40 = 3/10`
ii. `frac(12 + 13)(40)= 5/8`
Question 5
A garage repaired 132 vehicles last month. The number of vehicles that required electrical (E), mechanical (M) and bodywork (B) repairs are given in the diagram opposite.

Find the probability that a randomly selected vehicle required:
a. mechanical or bodywork repairs
b. no bodywork repairs
c. exactly two types of repair.
a. `frac(13 + 47 + 5 + 18 + 11 + 26)(132) = 10/11` or `frac(132-12)(132) = 10/11`
b. `frac(12 + 13 + 47)(312) = 6/11` or `frac(132 - (11 + 5 + 18 + 26)(132) = 6/11`
c. `frac(13 + 11 + 18)(132) = 7/22` or `frac(132-(12+47 + 26 + 5))(132) = 7/22`
Question 6
Events X and Y are such that P(X) = 0.5, P(Y) = 0.6 and P(`X cap Y)` = 0.2
a. State, giving a reason, whether events X and Y are mutually exclusive.
b. Using a Venn diagram, or otherwise, find `P(X capY)`.
c. Find the probability that X or Y, but not both, occurs.
a. X and Y are not mutually exclusive because `P(X cap Y) ne 0`
Also, X and Y are not mutually exclusive because `P(X cap Y) ne 0` and because `P(X cap Y) ne P(X) + P(Y)`
b. 0.5 + 0.6 - 0.2 = 0.9
c. (0.5 - 0.2) + (0.6 - 0.2) = 0.7
Question 7
Each of 27 tourists was asked which of the countries Angola (A), Burundi (B) and Cameroon (C) they had visited. Of the group, 15 had visited Angola; 8 had visited Burundi; 12 had visited Cameroon; 2 had visited all three countries; and 21 had visited only one. Of those who had visited Angola, 4 had visited only one other country. Of those who had not visited Angola, 5 had visited Burundi only. All of the tourists had visited at least one of these countries.
a. Draw a fully labelled Venn diagram to illustrate this information.
b. Find the number of tourists in set B′ and describe them.
c. Describe the tourists in set `(A cup B) cap C'`and state how many there are.
d. Find the probability that a randomly selected tourist from this group had visited at least two of these three countries.
a.
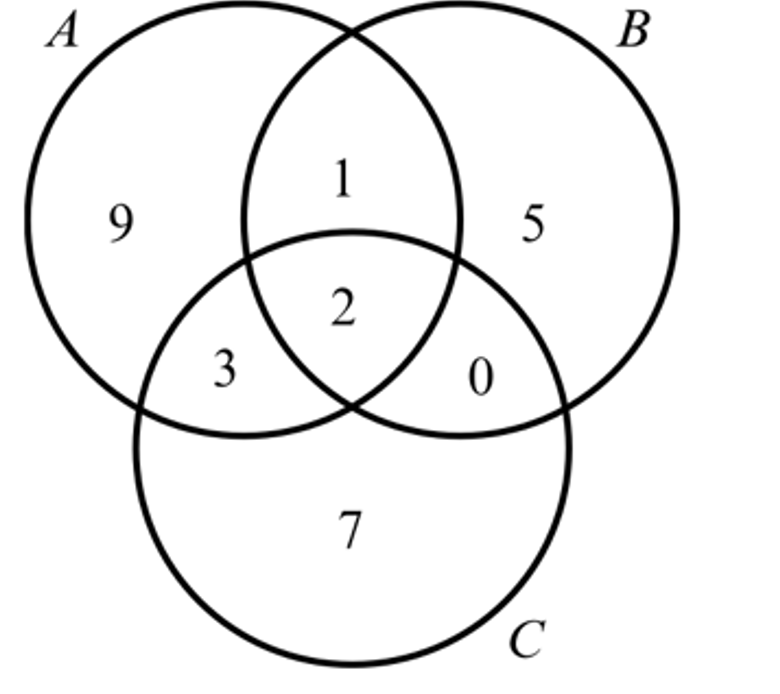
b. 9 + 3 + 7 = 19, they had not visited Burundi
c. They had visited Angola or Burundi, but not Cameroon;
9 + 1 + 5 = 15
d. `frac(1 +2 +3 + 0)(27) = 2/9` or `frac(27 - (9+5+7))(27) = 2/9`
Question 8
The probabilities that a team wins, draws or loses any particular game are 0.6, 0.1 and 0.3, respectively.
a . Find the probability that the team wins at least one of its next two games.
b. If 2 points are awarded for a win, 1 point for a draw and 0 points for a loss, find the probability that the team scores a total of more than 1 point in its next two games.
a. `P(W, W') + P(W', W) + P(W, W) = 0.6*0.4 + 0.4*0.6 + 0.6* 0.6 = 0.84`
“At least one” has the same meaning as “not none”, so we could use `1- P(W', W') = 1 - 0.4*0.4 = 0.84`
b. `1- [P(L,L) + P(L, D) + P(D,L)] = 1- [(0.3*0.3) + (0.3*0.3) + 0.1 *0.3)] = 0.85`
Question 9
A biased die in the shape of a pyramid has five faces marked 1, 2, 3, 4 and 5. The possible scores are 1, 2, 3, 4 and 5 and `P(x) = frac(k-x)(25)`,
where k is a constant.
a. Find, in terms of k, the probability of scoring:
i. 5
ii. less than 3
b. The die is rolled three times and the scores are added together. Evaluate k and find the probability that the sum of the three scores is less than 5.
a. i. Substituting x = 5 gives
`P(5) = frac(k-5)(25)`
ii. P(score < 3) = P(1 or 2) = `frac(k-2)(25) + frac(k-1)(25) = frac(2k-3)(25)`
b. Sum of probabilities is
`frac(k -1 + k -2 + k -3 + k-4+ k-5)(25) = 1`
Giving 5k - 15 = 25, so k = 8
P(sum <5) = P(1,1,1) + P(1,1,2) P(1,2,1) + P(2,1,1)
P(sum <5) = `(7/25)^3n+ 3*(7/25*7/25*6/25) = 49/625`or 0.0784
Question 10
A,B and C are independent events, and it is given that `P(A capB) = 0. 35, P(B cap C) = 0.56` and `P(A capC) = 0.4`
a. Express in terms of:
i. P(B)
ii. P(C)
b. Use your answers to part a to find:
i. P(B)
ii. P(A')
iii. `P(B' capC')`
a.
i. `P(A) = 0.35/ (P(B))`
ii. `P(A) = 0.4/(P(C)`
b.
i. `P(B' capC')` = `P(B)*P(C) = 0.56`, so P(B) = `0.56/(P(C)`
`P(C) = frac(0.4*P(B))(0.35` gives `P(B) = frac(0.56*0.35)(0.4*P(B)`
`[P(B)]^2 = frac(0.56*0.35)(0.4) = 0.49`, so P(B) = 0.7
ii. P(A') = 1 - 0.5 = 0.5
iii. `P(B' capC')` = `P(B')*P(C')`
`P(B' capC')` = `(1-0.7)*(1-0.8) = 0.06`
Question 11
Two ordinary fair dice are rolled.
Event X is the product of the two numbers obtained is odd.
EventY is the sum of the two numbers obtained is a multiple of 3.
a. Determine, giving reasons for your answer, whether X and Y are independent.
b. Are events X and Y mutually exclusive? Justify your answer.
a. P(X and Y) `1/12`, P(X) = `1/4`, P(Y) = `1/3` and `1/12 = 1/4 * 1/3`
P`(XcapY) = P(X)*P(Y)`, so X and Y are independent
b. X and Y are not mutually exclusive; X and Y both occur when, for example, 1 and 5 are rolled, i.e.
`P(XcapY) ne 0`
Question 12
One hundred children were each asked whether they have brothers (B) and whether they have sisters (S). Their responses are given in the Venn diagram.

Find the probability that a randomly selected child has:
a. sisters, given that they have brothers
b. brothers, given that they do not have sisters
c. sisters or brothers, given that they do not have both.
a. 16 + 48 = 64 have brothers and 48 of these have sisters:
`48/64 = 3/4`
b. 16 + 12 = 28 do not have sisters, and 16 of these have brothers:
`16/28 = 4/7`
c. 16 + 24 + 12 = 52 do not have both, and 16 + 24 = 40 of these have brothers or sisters:
`40/52 = 10/13`
Question 13
Anya calls Zara once each evening before she goes to bed. She calls Zara’s mobile phone with probability 0.8 or her landline. The probability that Zara answers her mobile phone is 0.74, and the probability that she answers her landline is y. This information is displayed in the tree diagram shown.

a. Given that Zara answers 68% of Anya’s calls, find the value of y.
b. Given that Anya’s call is not answered, find the probability that it is made to Zara’s landline.
a. `(0.8*0.74) + (1-0.8)y = 0.68`
0.592 + 0.2y = 0.68, which gives y = 0.44
b. P(call not answered) = (0.8*0.26) + (0.2*0.56)
P(not answered) = `frac(0.2*0.56)(0.8*0.26+0.2*0.56)= 0.35`or `7/20`
Question 14
Every Friday, Arif offers to take his sons to the beach or to the park. The sons refuse an offer to the beach with probability 0.65 and accept an offer to the park with probability 0.85. The probability that Arif offers to take them to the beach is x. This information is shown in the tree diagram

a. Find the value of x, given that 33% of Arif’s offers are refused
b. Given that Arif’s offer is accepted, find the probability that he offers to take his sons to the park
a. 0.65x + 0.15(1-x) = 0.33 gives x = 0.36
b. P(offer accepted) = 0.36*0.35 + 0.64*0.85
P(accepted) = `frac(0.64*0.85)(0.36*0.35 + 0.64*0.85) = 0.812` or `272/335`
Question 15
Three friends, Rick, Brenda and Ali, go to a football match but forget to say which entrance to the ground they will meet at. There are four entrances, A, B, C and D. Each friend chooses an entrance independently.
a. Find the probability that at least 2 friends will choose entrance B.
b. Find the probability that the three friends will all choose the same entrance.
a.
|
| A | B | C | D |
| A(li) | `2/35` | `2/35` | `10/35` | `21/35` |
| B(renda) | `1/4` | `1/4` | `1/4` | `1/4` |
| R(ick) | `3/9` | `2/9` | `2/9` | `2/9` |
P(at least two choose B) = P(two choose B) + P(thre choose B)
= P(abr') + P(ab'r) + P(a'br) + P(abr)
= `(2/35*1/4*7/9)+(2/35*3/4*2/9)+(33/35*1/4*2/9)+(2/35*1/4*2/9)` = `8/105` or 0.0762
b. `P(All A) + P(all B) +P(all C) + P(all D) `
`(2/35*1/4*3/9)+ (2/35*1/4*2/9)+(10/35*1/4*2/9)+(21/35*1/4*2/9) = 2/35`
Question 16
Maria chooses toast for her breakfast with probability 0.85. If she does not choose toast then she has a bread roll. If she chooses toast then the probability that she will have jam on it is 0.8. If she has a bread roll then the probability that she will have jam on it is 0.4.
a. Draw a fully labelled tree diagram to show this information.
b. Given that Maria did not have jam for breakfast, find the probability that she had toast.
a. Let T, B and X represent toast, bread and not jam, respectively:
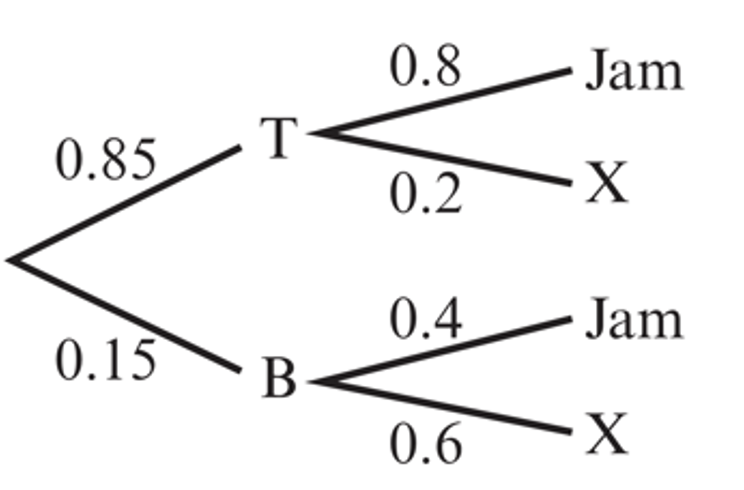
b. P(X) = P(T and X) + P(B and X) = `(0.85*0.2) + (0.15*0.6)`
P(X) = `frac(P(X and T))(P(X)) = frac(0.85*0.2)((0.85*0.2) +(0.15*0.6)) = 17/26`
Question 17
Ronnie obtained data about the gross domestic product (GDP) and the birth rate for 170 countries. He classified each GDP and each birth rate as either ‘low’, ‘medium’ or ‘high’. The table shows the number of countries in each category.
|
| Birth rate | |||
| Low | Medium | High | ||
| GDP | Low | 3 | 5 | 45 |
| Medium | 20 | 42 | 12 | |
| High | 35 | 8 | 0 | |
One of these countries is chosen at random.
a. Find the probability that the country chosen has a medium GDP
b. Find the probability that the country chosen has a low birth rate, given that it does not have a
medium GDP
c. State with a reason whether or not the events ‘the country chosen has a high GDP’ and ‘the country chosen has a high birth rate’ are exclusive
One country is chosen at random from those countries which have a medium GDP and then a different country is chosen at random from those which have a medium birth rate.
d. Find the probability that both countries chosen have a medium GDP and a medium birth rate
a. `frac(20 + 42 + 12)(170) = 37/85` or 0.435
b. `frac(3+35)(3+5+45+35+8) = 19/48`or 0.396
c. They are (mutually) exclusive;
P(high GDP and high birth rate) = 0
d. `42/(20+42 +12) * frac(41)(5+41+8)= 42/74*41/54= 287/666` or 0.431
Question 18
Two ordinary fair dice are rolled. Event A is ‘the sum of the numbers rolled is 2, 3 or 4’. Event B is ‘the absolute difference between the numbers rolled is 2, 3 or 4’.
a. When the dice are rolled, they show a 1 and a 3. Explain why this result shows that events A and B are not mutually exclusive.
b. Explain how you know that `P(A capB) = 1/18`
c. Determine whether events A and B are independent.
a. Rolling a 1 and a 3 is favorable to A and to B
b. Exactly two of the 36 equally-likely outcomes i.e. (1,3) and (3,1), are favorable to A and to B, so
`P(A cap B) = 2/36 = 1/18`
c. P(A) = `1/6`, P(B) = `1/2`, `P(A capB) = 1/18`
`1/18 ne 1/6*1/2 = 1/12`
So `P(A capB) ne P(A)*P(B)`and, therefore, A and B arenot independent.
Question 19
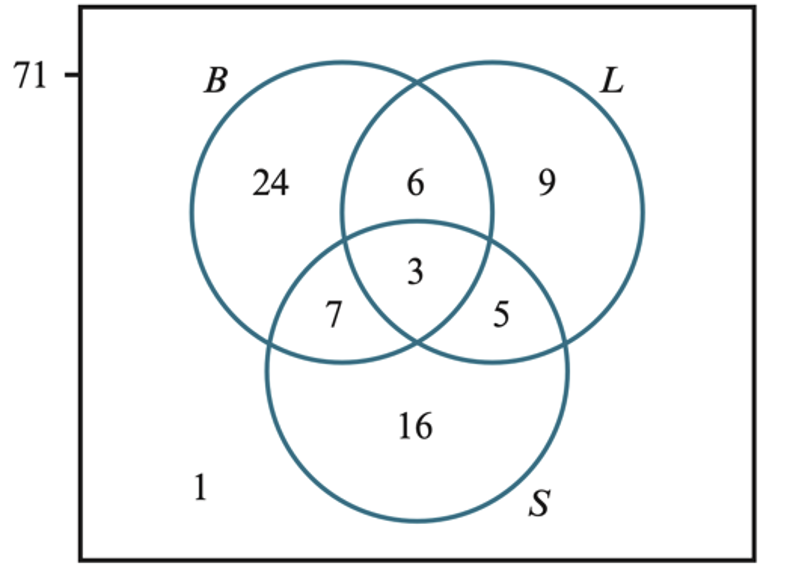
Bookings made at a hotel include a room plus any meal combination of breakfast (B), lunch (L) and supper (S). The Venn diagram opposite shows the number of each type of booking made by 71 guests on Friday.

a. A guest who has not booked all three meals is selected at random.
Find the probability that this guest:
i. has booked breakfast or supper
ii. has not booked supper, given that they have booked lunch.
b. Find the probability that two randomly selected guests have both booked lunch, given that they have both booked at least two meals.
a.
i. `frac(7+24+6+16+5)(71-3) = 29/34`
ii. `frac(6+9)(6+9+5) = 3/4`
b. `frac(6+5+3)(7+6+5+3)*frac(6+5+3-1)(7+6+5+3-1) = 14/21*13/20= 13/20`
Question 20
The following table shows the numbers of IGCSE (I) and A Level (A) examinations passed by a group of university students.
|
| IGCSEs (I) | ||||||
| 5 | 6 | 7 | 8 | 9 | 10 | ||
| A Levels (A) | 2 | 13 | 9 | 5 | 4 | 2 | 0 |
| 3 | 7 | 8 | 9 | 6 | 1 | 0 | |
| 4 | 0 | 0 | 1 | 0 | 1 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | |
a. For a student selected at random, find:
i. P(A < 4)
ii. P(I + A > 10)
b. Six students who all have at least three A Level passes are selected at random.
Find the greatest possible range of the total number of IGCSE passes that they could have.
a.i. `frac(6+2)(20+17+14+10+3)= 1/8`
ii. `frac(2+1)(1+6+2+1+1+1) = 1/4`
b. Minimum possible total is `6*5 = 30`
Maximum possible total is `10+9+9+8+8+8 = 52`
Greatest possible range is 52 - 30 = 22
Question 1
United’s manager estimates that the team has a 65% chance of winning any particular game and an 85% chance of not drawing any particular game.
a. What are the manager’s estimates most likely to be based on?
b. If the team plays 40 games this season, find the manager’s expectation of the number of games the team will lose.
c. If the team loses one game more than the manager expects this season, explain why this does not necessarily mean that they performed below expectation.
Question 2
A numbered wheel is divided into eight sectors of equal size, as shown. The wheel is spun until it stops with the arrow pointing at one of the numbers. Axel decides to spin the wheel 400 times.

a. Find the number of times the arrow is not expected to point at a 4.
b. How many more times must Axel spin the wheel so that the expected number of times that the arrow points at a 4 is at least 160?
Question 3
In a group of 25 boys, nine are members of the chess club (C ), eight are members of the debating club (D) and 10 are members of neither of these clubs. This information is shown in the Venn diagram.

a. Find the values of a, b and c.
b. Find the probability that a randomly selected boy is:
i. a member of the chess club or the debating club
ii. a member of exactly one of these clubs.
Question 4
Forty girls were asked to name the capital of Cuba and of Hungary; 19 knew the capital of Cuba, 20 knew the capital of Hungary and seven knew both.
a. Draw a Venn diagram showing the number of girls who knew each of these capitals.
b. Find the probability that a randomly selected girl knew:
i. the capital of Cuba but not of Hungary
ii. just one of these capitals.
Question 5
A garage repaired 132 vehicles last month. The number of vehicles that required electrical (E), mechanical (M) and bodywork (B) repairs are given in the diagram opposite.

Find the probability that a randomly selected vehicle required:
a. mechanical or bodywork repairs
b. no bodywork repairs
c. exactly two types of repair.
Question 6
Events X and Y are such that P(X) = 0.5, P(Y) = 0.6 and P(`X cap Y)` = 0.2
a. State, giving a reason, whether events X and Y are mutually exclusive.
b. Using a Venn diagram, or otherwise, find `P(X capY)`.
c. Find the probability that X or Y, but not both, occurs.
Question 7
Each of 27 tourists was asked which of the countries Angola (A), Burundi (B) and Cameroon (C) they had visited. Of the group, 15 had visited Angola; 8 had visited Burundi; 12 had visited Cameroon; 2 had visited all three countries; and 21 had visited only one. Of those who had visited Angola, 4 had visited only one other country. Of those who had not visited Angola, 5 had visited Burundi only. All of the tourists had visited at least one of these countries.
a. Draw a fully labelled Venn diagram to illustrate this information.
b. Find the number of tourists in set B′ and describe them.
c. Describe the tourists in set `(A cup B) cap C'`and state how many there are.
d. Find the probability that a randomly selected tourist from this group had visited at least two of these three countries.
Question 8
The probabilities that a team wins, draws or loses any particular game are 0.6, 0.1 and 0.3, respectively.
a . Find the probability that the team wins at least one of its next two games.
b. If 2 points are awarded for a win, 1 point for a draw and 0 points for a loss, find the probability that the team scores a total of more than 1 point in its next two games.
Question 9
A biased die in the shape of a pyramid has five faces marked 1, 2, 3, 4 and 5. The possible scores are 1, 2, 3, 4 and 5 and `P(x) = frac(k-x)(25)`,
where k is a constant.
a. Find, in terms of k, the probability of scoring:
i. 5
ii. less than 3
b. The die is rolled three times and the scores are added together. Evaluate k and find the probability that the sum of the three scores is less than 5.
Question 10
A,B and C are independent events, and it is given that `P(A capB) = 0. 35, P(B cap C) = 0.56` and `P(A capC) = 0.4`
a. Express in terms of:
i. P(B)
ii. P(C)
b. Use your answers to part a to find:
i. P(B)
ii. P(A')
iii. `P(B' capC')`
Question 11
Two ordinary fair dice are rolled.
Event X is the product of the two numbers obtained is odd.
EventY is the sum of the two numbers obtained is a multiple of 3.
a. Determine, giving reasons for your answer, whether X and Y are independent.
b. Are events X and Y mutually exclusive? Justify your answer.
Question 12
One hundred children were each asked whether they have brothers (B) and whether they have sisters (S). Their responses are given in the Venn diagram.

Find the probability that a randomly selected child has:
a. sisters, given that they have brothers
b. brothers, given that they do not have sisters
c. sisters or brothers, given that they do not have both.
Question 13
Anya calls Zara once each evening before she goes to bed. She calls Zara’s mobile phone with probability 0.8 or her landline. The probability that Zara answers her mobile phone is 0.74, and the probability that she answers her landline is y. This information is displayed in the tree diagram shown.

a. Given that Zara answers 68% of Anya’s calls, find the value of y.
b. Given that Anya’s call is not answered, find the probability that it is made to Zara’s landline.
Question 14
Every Friday, Arif offers to take his sons to the beach or to the park. The sons refuse an offer to the beach with probability 0.65 and accept an offer to the park with probability 0.85. The probability that Arif offers to take them to the beach is x. This information is shown in the tree diagram

a. Find the value of x, given that 33% of Arif’s offers are refused
b. Given that Arif’s offer is accepted, find the probability that he offers to take his sons to the park
Question 15
Three friends, Rick, Brenda and Ali, go to a football match but forget to say which entrance to the ground they will meet at. There are four entrances, A, B, C and D. Each friend chooses an entrance independently.
a. Find the probability that at least 2 friends will choose entrance B.
b. Find the probability that the three friends will all choose the same entrance.
Question 16
Maria chooses toast for her breakfast with probability 0.85. If she does not choose toast then she has a bread roll. If she chooses toast then the probability that she will have jam on it is 0.8. If she has a bread roll then the probability that she will have jam on it is 0.4.
a. Draw a fully labelled tree diagram to show this information.
b. Given that Maria did not have jam for breakfast, find the probability that she had toast.
Question 17
Ronnie obtained data about the gross domestic product (GDP) and the birth rate for 170 countries. He classified each GDP and each birth rate as either ‘low’, ‘medium’ or ‘high’. The table shows the number of countries in each category.
|
| Birth rate | |||
| Low | Medium | High | ||
| GDP | Low | 3 | 5 | 45 |
| Medium | 20 | 42 | 12 | |
| High | 35 | 8 | 0 | |
One of these countries is chosen at random.
a. Find the probability that the country chosen has a medium GDP
b. Find the probability that the country chosen has a low birth rate, given that it does not have a
medium GDP
c. State with a reason whether or not the events ‘the country chosen has a high GDP’ and ‘the country chosen has a high birth rate’ are exclusive
One country is chosen at random from those countries which have a medium GDP and then a different country is chosen at random from those which have a medium birth rate.
d. Find the probability that both countries chosen have a medium GDP and a medium birth rate
Question 18
Two ordinary fair dice are rolled. Event A is ‘the sum of the numbers rolled is 2, 3 or 4’. Event B is ‘the absolute difference between the numbers rolled is 2, 3 or 4’.
a. When the dice are rolled, they show a 1 and a 3. Explain why this result shows that events A and B are not mutually exclusive.
b. Explain how you know that `P(A capB) = 1/18`
c. Determine whether events A and B are independent.
Question 19
Bookings made at a hotel include a room plus any meal combination of breakfast (B), lunch (L) and supper (S). The Venn diagram opposite shows the number of each type of booking made by 71 guests on Friday.

a. A guest who has not booked all three meals is selected at random.
Find the probability that this guest:
i. has booked breakfast or supper
ii. has not booked supper, given that they have booked lunch.
b. Find the probability that two randomly selected guests have both booked lunch, given that they have both booked at least two meals.
Question 20
The following table shows the numbers of IGCSE (I) and A Level (A) examinations passed by a group of university students.
|
| IGCSEs (I) | ||||||
| 5 | 6 | 7 | 8 | 9 | 10 | ||
| A Levels (A) | 2 | 13 | 9 | 5 | 4 | 2 | 0 |
| 3 | 7 | 8 | 9 | 6 | 1 | 0 | |
| 4 | 0 | 0 | 1 | 0 | 1 | 0 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 | |
a. For a student selected at random, find:
i. P(A < 4)
ii. P(I + A > 10)
b. Six students who all have at least three A Level passes are selected at random.
Find the greatest possible range of the total number of IGCSE passes that they could have.