Question 1
Distinguish between a scalar and a vector quantity.
Easy
Mark as Complete
Mark Scheme
Question 2
Which of the following is a vector?
A. Electric charge.
B. Momentum.
C. Power.
D. Work.
Easy
Mark as Complete
Mark Scheme
Question 3
Two physical quantities P and Q are added. Sum of P and Q is R, as shown. Which quantity could be represented by P and by Q? 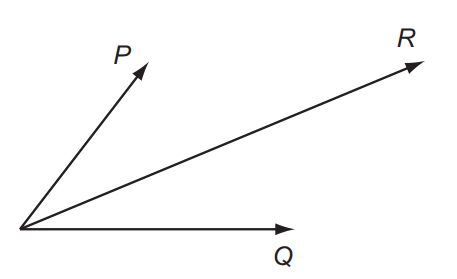
A. Kinetic.
B. Power.
C. Speed.
D. Velocity.
Easy
Mark as Complete
Mark Scheme
Question 4
Which option contains only scalar quantities?
A. Area, length, displacement.
B. Kinetic energy, speed, power.
C. Potential energy, momentum, time.
D. Velocity, distance, temperature.
Easy
Mark as Complete
Mark Scheme
Question 5
The diagram shows a displacement vector.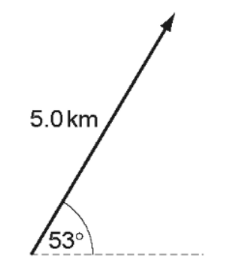 What is the vertical component of this displacement vector?
What is the vertical component of this displacement vector?
A. 3.0 km.
B. 4.0 km.
C. 5.0 km.
D. 6.6 km.
Easy
Mark as Complete
Mark Scheme
Question 6
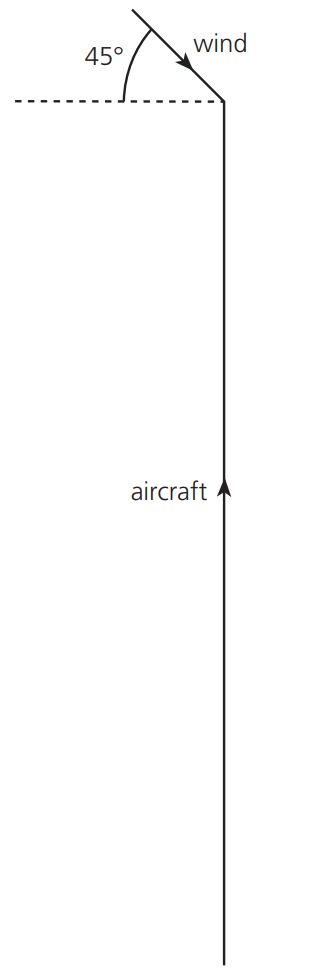
Velocity vector diagram for an aircraft heading due north is shown to scale in the figure below. There is a wind blowing from the north-west. The speed of the wind is 36 m.s-1 and the speed of the aircraft is 250 m.s-1
a. Make a copy of the figure below. Draw an arrow to show the direction of the resultant velocity of the aircraft.
b. Determine the magnitude of the resultant velocity of the aircraft.
Medium
Mark as Complete
Mark Scheme
Question 7
A girl walks at a speed of 1.5 m.s-1 for 1.0 minutes in a direction of 35° north of east. How far east does she walk?
A. 52 m.
B. 63 m.
C. 74 m.
D. 90 m.
Medium
Mark as Complete
Mark Scheme
Question 8
Which pair of quantities contains both scalar and vector quantity?
A. Impulse and angular momentum.
B. Work and frequency.
C. Electromagnetic force and force.
D. Current density and current.
Medium
Mark as Complete
Mark Scheme
Question 9
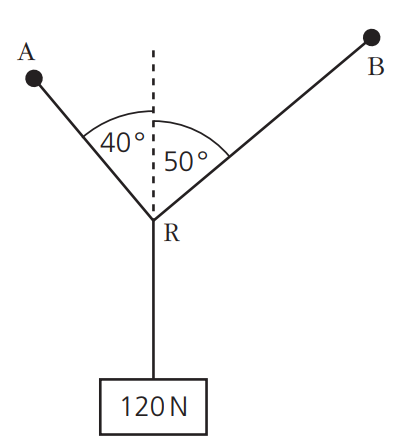
A mass of weight 120 N is hung from two strings as shown in figure below. Determine, by scale drawing or by calculation, the tension in:
a. RA.
b. RB.
Hard
Mark as Complete
Mark Scheme
Question 10
A fielder in a cricket match throws the ball to the wicket-keeper. At one moment of time, the ball has a horizontal velocity of 16 m.s-1 and a velocity in the vertically upward direction of 8.9 m.s-1.
a. Determine, for the ball:
i. Its resultant speed.
ii. The direction in which it is travelling relative to the horizontal.
b. During the flight of the ball to the wicket-keeper, the horizontal velocity remains unchanged. The speed of the ball at the moment when the wicket-keeper catches it is 19 m.s-1. Calculate, for the ball just as it is caught:
i. Its vertical speed.
ii. The angle that the path of the ball makes with the horizontal.
Hard
Mark as Complete
Mark Scheme
Question 1
Distinguish between a scalar and a vector quantity.
Vector quantity has magnitude, unit, and direction. They may not be added algebraically.
Scalar quantity has magnitude and unit. They can be added algebraically.
Question 2
Which of the following is a vector?
A. Electric charge.
B. Momentum.
C. Power.
D. Work.
Answer: B
Scalars are quantities that have magnitude and unit; they are independent of direction. Vectors have all three of them. Momentum is the product of the mass and velocity of an object p = mv. Momentum is a vector quantity since it has a direction as well as a magnitude.
Question 3
Two physical quantities P and Q are added. Sum of P and Q is R, as shown. Which quantity could be represented by P and by Q? 
A. Kinetic.
B. Power.
C. Speed.
D. Velocity.
Answer: D
Since P and Q are added to give R, we can represent this situation as: `vec P + vec Q =vec R`.
From the given options, kinetic energy, speed and power (rate of doing work) are scalar quantities whereas velocity is vector quantity. When adding two vectors, the result can be another vector. Therefore, P and Q could be represented by vector quantities.
Question 4
Which option contains only scalar quantities?
A. Area, length, displacement.
B. Kinetic energy, speed, power.
C. Potential energy, momentum, time.
D. Velocity, distance, temperature.
Answer: B
Vector quantities: Displacement, momentum, velocity.
Scalar quantities: Area, length, kinetic energy, speed, power, potential energy, yime, distance, temperature.
Question 5
The diagram shows a displacement vector. What is the vertical component of this displacement vector?
What is the vertical component of this displacement vector?
A. 3.0 km.
B. 4.0 km.
C. 5.0 km.
D. 6.6 km.
Answer: B
`d_v=5.0xxsin(53^o)="4.0 km"`
Question 6
Velocity vector diagram for an aircraft heading due north is shown to scale in the figure below. There is a wind blowing from the north-west. The speed of the wind is 36 m.s-1 and the speed of the aircraft is 250 m.s-1
a. Make a copy of the figure below. Draw an arrow to show the direction of the resultant velocity of the aircraft.
b. Determine the magnitude of the resultant velocity of the aircraft.

a.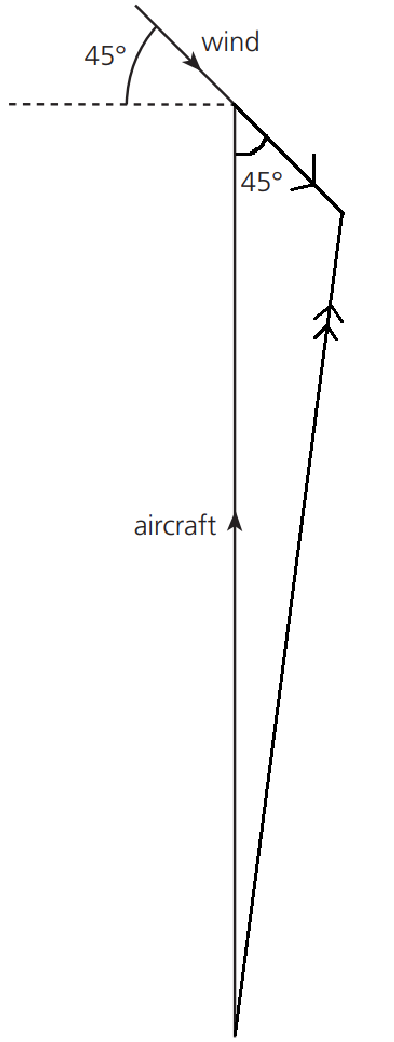
b. Using cosine rule:
`v^2=v""_"wind"^2+v""_"aircraft"^2-2xxv_"wind"xxv_"aircraft"xxcostheta`
`=> v=sqrt(36^2+250^2-2xx36xx250xxcos(45^o)) =226 " m"."s"^-1`
Question 7
A girl walks at a speed of 1.5 m.s-1 for 1.0 minutes in a direction of 35° north of east. How far east does she walk?
A. 52 m.
B. 63 m.
C. 74 m.
D. 90 m.
Answer: C
Convert 1 minute to seconds: 1 minute = 60 seconds.
The horizontal component of the girl's velocity:
`v_x=vxxcos(theta)` where, `v=1.5 m.s^(-1)` and `theta=35^(o)`.
`v_x=1.5xxcos(35^o)=1.2287 " m"."s"^(-1)`
The distance traveled east:
`d_"east"= v_x xx t` where `t=60" s"`
Thus, `d_"east"=1.2287xx60=73.72 " m"`
Question 8
Which pair of quantities contains both scalar and vector quantity?
A. Impulse and angular momentum.
B. Work and frequency.
C. Electromagnetic force and force.
D. Current density and current.
The answer is C.
A. Incorrect: Impulse and angular momentum. Impulse is defined as the change in momentum of an object, which is equal to the product of force and the time interval. Angular momentum is defined as the product of mass linear velocity and radius and it is not a scalar quantity nor a vector quantity.
B. Incorrect: Work and frequency, The work is defined as the product of force and displacement and work is a scalar quantity as the dot product of force and displacement is always a scalar quantity. Frequency is defined as the number of oscillations made per second. Frequency is a scalar quantity.
C. Correct: Electromagnetic force and force. Electromagnetic force is defined as the energy per unit charge and is a scalar quantity. Electromagnetic force is a scalar quantity. Force is defined as the product of mass and acceleration and force is a vector quantity. This is the pair in which one physical quantity is scalar and other is vector. The correct answer is electromagnetic force and force.
D. Incorrect: Current density and current. Current is defined as a moving stream of charged particles ions and electrons from one point to another point. Current is a scalar quantity. Current density is defined as the amount of charge per unit time that flows through a unit area of cross section. The current density is vector quantity.
Question 9
A mass of weight 120 N is hung from two strings as shown in figure below. Determine, by scale drawing or by calculation, the tension in:
a. RA.
b. RB.

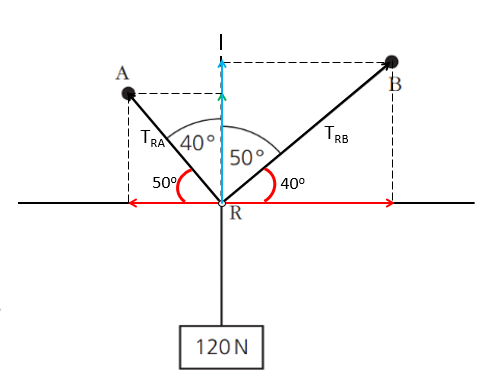
Upward components from RA and RB must balance the weight:
`T_(RA) xx cos(40°) + T_(RB) xx cos(50°) = 120`
Horizontal components must cancel each other:
`T_(RB) xx sin(50°) = T_(RA) xx sin(40°)`
Solve for TRA: `T_(RA) = T_(RB) xx sin(50°)/sin(40°) = T_RB xx 1.191`
Substitute into vertical equation:
`T_(RB)xx1.191 xx cos(40°) + T_(RB) xx cos(50°) = 120`
Tension in RB:
`T_(RB) = 120 / 1.5553 ≈ "77.1 N"`
Tension in RA:
`T_(RA) = 1.191xx77.1="91.8 N"`
Question 10
A fielder in a cricket match throws the ball to the wicket-keeper. At one moment of time, the ball has a horizontal velocity of 16 m.s-1 and a velocity in the vertically upward direction of 8.9 m.s-1.
a. Determine, for the ball:
i. Its resultant speed.
ii. The direction in which it is travelling relative to the horizontal.
b. During the flight of the ball to the wicket-keeper, the horizontal velocity remains unchanged. The speed of the ball at the moment when the wicket-keeper catches it is 19 m.s-1. Calculate, for the ball just as it is caught:
i. Its vertical speed.
ii. The angle that the path of the ball makes with the horizontal.
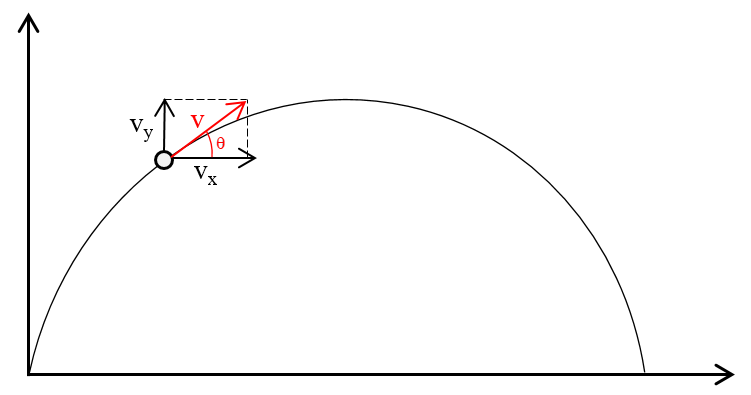 a.
a.
i. Use the Pythagorean theorem: `v = sqrt(16^2 + 8.9^2) = 18.3 " m"."s"^-1`
ii. The angle `theta = tan^(-1)((v_y)/(v_x)) = tan^(-1)((8.9)/(16)) = tan^(-1)(0.55625) = 29.1^o`
b.
i. Vertical speed:
`v_y = sqrt(v^2 - v_x^2) = sqrt(19^2 - 16^2) = sqrt(361 - 256) = sqrt(105)= 10.25 " m"."s"^-1`
ii. Direction (angle with horizontal):
`theta = tan^(-1)((v_y)/(v_x)) = tan^(-1)((10.25)/(16)) =tan^(-1)(0.6406) =32.7^o`
Question 1
Distinguish between a scalar and a vector quantity.
Question 2
Which of the following is a vector?
A. Electric charge.
B. Momentum.
C. Power.
D. Work.
Question 3
Two physical quantities P and Q are added. Sum of P and Q is R, as shown. Which quantity could be represented by P and by Q? 
A. Kinetic.
B. Power.
C. Speed.
D. Velocity.
Question 4
Which option contains only scalar quantities?
A. Area, length, displacement.
B. Kinetic energy, speed, power.
C. Potential energy, momentum, time.
D. Velocity, distance, temperature.
Question 5
The diagram shows a displacement vector. What is the vertical component of this displacement vector?
What is the vertical component of this displacement vector?
A. 3.0 km.
B. 4.0 km.
C. 5.0 km.
D. 6.6 km.
Question 6
Velocity vector diagram for an aircraft heading due north is shown to scale in the figure below. There is a wind blowing from the north-west. The speed of the wind is 36 m.s-1 and the speed of the aircraft is 250 m.s-1
a. Make a copy of the figure below. Draw an arrow to show the direction of the resultant velocity of the aircraft.
b. Determine the magnitude of the resultant velocity of the aircraft.

Question 7
A girl walks at a speed of 1.5 m.s-1 for 1.0 minutes in a direction of 35° north of east. How far east does she walk?
A. 52 m.
B. 63 m.
C. 74 m.
D. 90 m.
Question 8
Which pair of quantities contains both scalar and vector quantity?
A. Impulse and angular momentum.
B. Work and frequency.
C. Electromagnetic force and force.
D. Current density and current.
Question 9
A mass of weight 120 N is hung from two strings as shown in figure below. Determine, by scale drawing or by calculation, the tension in:
a. RA.
b. RB.

Question 10
A fielder in a cricket match throws the ball to the wicket-keeper. At one moment of time, the ball has a horizontal velocity of 16 m.s-1 and a velocity in the vertically upward direction of 8.9 m.s-1.
a. Determine, for the ball:
i. Its resultant speed.
ii. The direction in which it is travelling relative to the horizontal.
b. During the flight of the ball to the wicket-keeper, the horizontal velocity remains unchanged. The speed of the ball at the moment when the wicket-keeper catches it is 19 m.s-1. Calculate, for the ball just as it is caught:
i. Its vertical speed.
ii. The angle that the path of the ball makes with the horizontal.