Question 1
The angle between two forces, each of magnitude 5.0 N, is 120°.
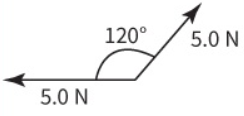
What is the magnitude of the resultant of these two forces?
Easy
Mark as Complete
Mark Scheme
Question 2
This diagram shows an object with two forces acting on it. The forces are at 90° to each other:
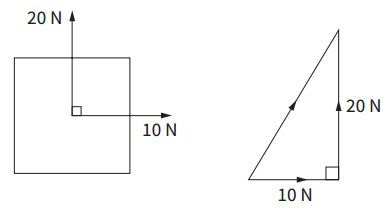
The diagram also shows the triangle we use to add these forces. In this case, it is sufficient to sketch the triangle.
a. Which side of the triangle represents the resultant force acting on the object?
b. Calculate the magnitude of the resultant force.
c. Use trigonometry to calculate the angle of the resultant force to the horizontal.
Easy
Mark as Complete
Mark Scheme
Question 3
A uniform metre rule is pivoted at the 34.0 cm mark, as shown.
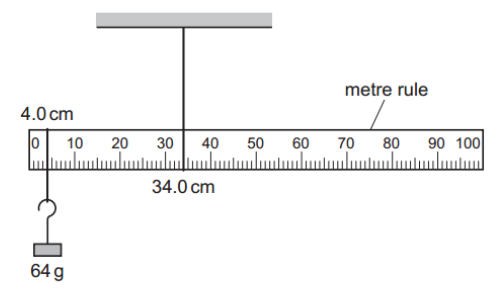
The rule balances when a 64 g mass is hung from the 4.0 cm mark. What is the mass of the metre rule?
A. 38 g.
B. 44 g.
C. 121 g.
D. 136 g.
Medium
Mark as Complete
Mark Scheme
Question 4
A uniform beam of length L is supported by two forces X and Y so that it is in equilibrium. The position of the forces is shown in figure.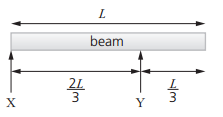 What is the ratio of the forces X:Y?
What is the ratio of the forces X:Y?
Medium
Mark as Complete
Mark Scheme
Question 5
A ship is pulled at a constant speed by two small boats, A and B, as shown. The engine of the ship does not produce any force.
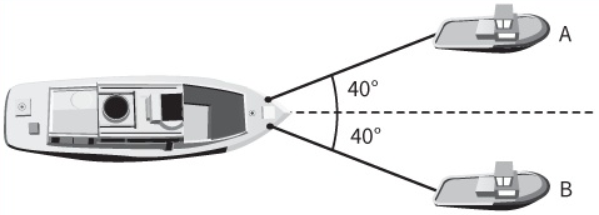
The tension in each cable between A and B and the ship is 4000 N. Draw a vector diagram to scale showing these three forces and use your diagram to find the value of the drag force on the ship.
Medium
Mark as Complete
Mark Scheme
Question 6
This free-body diagram shows three forces that act on a stone hanging at rest from two strings.
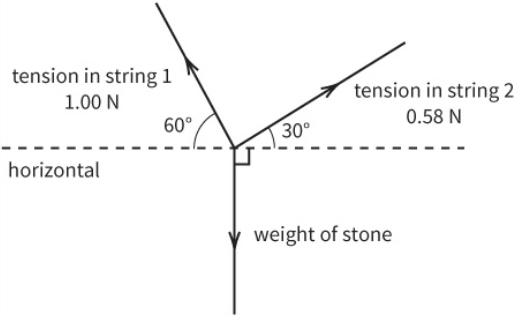
a. Calculate the horizontal component of the tension in each string. State why these two components are equal in magnitude?
b. Calculate the vertical component of the tension in each string.
c. Use your answer to part b to calculate the weight of the stone.
d. Draw a vector diagram of the forces on the stone. This should be a triangle of forces.
e. Use your diagram in part d to calculate the weight of the stone.
Medium
Mark as Complete
Mark Scheme
Question 7
Two children are using a long, uniform plank balanced on a cylindrical oil drum as a seesaw. The plank has a mass of 40 kg. It is 5.0 m in length and it is pivoted at a point 2.0 m from one end. Child A has a mass of 45 kg and sits at the end nearer to the pivot. Child B has a mass of 25 kg and sits at the other end.
a. Which one word in the question tells you that the plank’s centre of gravity is at its midpoint?
b. Draw a diagram to represent this situation. Show the forces acting as multiples of g, the acceleration due to gravity.
c. Determine the resultant moment acting on the plank and indicate its direction on your diagram.
Medium
Mark as Complete
Mark Scheme
Question 8
The diagram shows a ball of weight W hanging in equilibrium from a string.
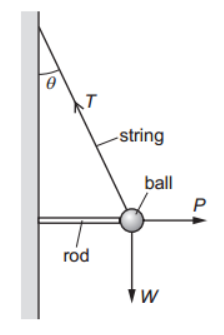
The string is at an angle `theta` to the vertical. The tension in the string is T. The ball is held away from the wall by a horizontal force P from a metal rod. Which relationship between the magnitudes of T, P and W is correct?
A. `P = T xx cos(theta) and W = T xx sin(theta)`.
B. `T = P + W`.
C. `T^2 = P^2 + W^2`.
D. `W = P xx tan(theta) and W = T xx cos(theta)`.
Hard
Mark as Complete
Mark Scheme
Question 9
A uniform rod AB is attached to a vertical wall at A. The rod is held horizontally by a string attached at B and to point C, as shown in figure.
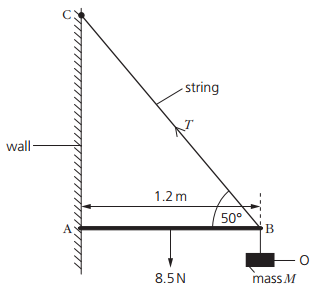
The angle between the rod and the string at B is 50°. The rod has length 1.2 m and weight 8.5 N. An object O of mass M is hung from the rod at B. The tension T in the string is 30 N.
a. Use the resolution of forces to calculate the vertical component of T.
b. State the principle of moments.
c. Use the principle of moments and take moments about A to show that the weight of the object O is 19 N.
Hard
Mark as Complete
Mark Scheme
Question 10
A flower basket is hung from the end of a uniform horizontal pole which projects from a wall, as shown. The pole is supported by a cable attached to a higher point on the wall.
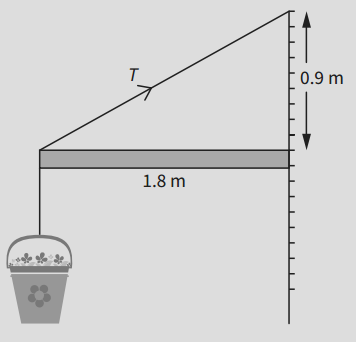
The pole has a mass of 10 kg; the flower basket has a mass of 14 kg. By taking moments about the right hand end of the pole, determine the value of the tension in the cable T.
Hard
Mark as Complete
Mark Scheme
Question 1
The angle between two forces, each of magnitude 5.0 N, is 120°.

What is the magnitude of the resultant of these two forces?
`R = sqrt(5.0^2 + 5.0^2 + 2 xx 5.0 xx 5.0 xx cos(120^o)) = sqrt(25 + 25 + 2 xx 25 xx (-0.5)) = sqrt(50 - 25) = sqrt(25) = 5.0 " " N`
Question 2
This diagram shows an object with two forces acting on it. The forces are at 90° to each other:

The diagram also shows the triangle we use to add these forces. In this case, it is sufficient to sketch the triangle.
a. Which side of the triangle represents the resultant force acting on the object?
b. Calculate the magnitude of the resultant force.
c. Use trigonometry to calculate the angle of the resultant force to the horizontal.
a. The hypotenuse.
b. Magtinude of resultant force:
`R = sqrt(F_1^2 + F_2^2) = sqrt(10^2 + 20^2) = sqrt(100 + 400) = sqrt(500) = "22.36 N"`
c. `tantheta = "opposite" / "adjacent" = F_y / F_x = 20 / 10 = 2`
`theta = tan^-12 ~~ 63.4^o`.
Question 3
A uniform metre rule is pivoted at the 34.0 cm mark, as shown.

The rule balances when a 64 g mass is hung from the 4.0 cm mark. What is the mass of the metre rule?
A. 38 g.
B. 44 g.
C. 121 g.
D. 136 g.
Answer: C
Distance from 4.0 cm to pivot (34.0 cm):
`r _1 =0.34−0.04="30 cm"`
`"Anticlockwise moment"=0.064xx9.8xx0.3="0.19 N.m"`
Distance from center of mass to pivot:
`r _2 =0.5−0.34="0.16 cm"`
`"Moment due to rule's weight (clockwise moment)" = mxx9.8xx0.16`
`"Clockwise moment = Anticlockwise moment"`
`0.19=mxx9.8xx0.16`
`m="0.121 kg" = "121 g"`.
Question 4
A uniform beam of length L is supported by two forces X and Y so that it is in equilibrium. The position of the forces is shown in figure. What is the ratio of the forces X:Y?
What is the ratio of the forces X:Y?
Force Y creates a clockwise moment:
`"Moment by Y" = Y xx (2L / 3)`
The weight W of the beam acts at the center (at L/2), creating an anticlockwise moment:
`"Moment by weight" = W xx (L / 2)`
Clockwise moment = anticlockwise moment:
`Y xx (2L / 3) = W xx (L / 2)`
Since the beam is in equilibrium:
`X + Y = W => X = W - Y = W - (3W / 4) = W / 4`
`X : Y = (W / 4) : (3W / 4) = 1 : 3`
Question 5
A ship is pulled at a constant speed by two small boats, A and B, as shown. The engine of the ship does not produce any force.

The tension in each cable between A and B and the ship is 4000 N. Draw a vector diagram to scale showing these three forces and use your diagram to find the value of the drag force on the ship.
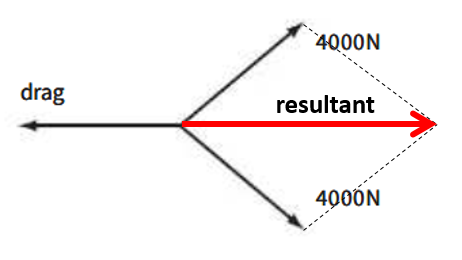
`"Magnitude of drag force" = "magnitude of resultant force"=2xx4000xxcos40^o="6128.36 N"`
Question 6
This free-body diagram shows three forces that act on a stone hanging at rest from two strings.

a. Calculate the horizontal component of the tension in each string. State why these two components are equal in magnitude?
b. Calculate the vertical component of the tension in each string.
c. Use your answer to part b to calculate the weight of the stone.
d. Draw a vector diagram of the forces on the stone. This should be a triangle of forces.
e. Use your diagram in part d to calculate the weight of the stone.
a.
`"Horizontal component of tension in string 1" = tension xx cos60^o = 1.0 xx cos60^o = "0.50 N" " to the left"`
`"Horizontal component of tension in string 2" = tension xx cos30^o = 0.58 xx cos30^o = "0.5 N" " to the right"`
These components cancel, as there is no resultant horizontal force.
b.
`"Vertical component of tension in string 1" = tension xx cos30^o = 1.0 xx cos30^o= "0.87 N" " upward"`
`"Vertical component of tension in string 2" = tension xx cos60^o= 0.58 xx cos60^o= "0.29 N" " upward"`
c. `"Weight is balanced by upward components of tensions" = 0.87 + 0.29 = "1.16 N" = "1.2 N"`
d.
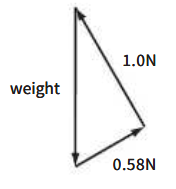
e.
By Pythagoras’ theorem, weight = 1.16 N = 1.2 N
Question 7
Two children are using a long, uniform plank balanced on a cylindrical oil drum as a seesaw. The plank has a mass of 40 kg. It is 5.0 m in length and it is pivoted at a point 2.0 m from one end. Child A has a mass of 45 kg and sits at the end nearer to the pivot. Child B has a mass of 25 kg and sits at the other end.
a. Which one word in the question tells you that the plank’s centre of gravity is at its midpoint?
b. Draw a diagram to represent this situation. Show the forces acting as multiples of g, the acceleration due to gravity.
c. Determine the resultant moment acting on the plank and indicate its direction on your diagram.
a. Uniform.
b.
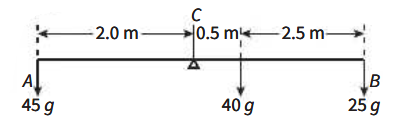
c. `"Resultant moment" = 3.0 xx 25g + 0.5 xx 40g - 2.0 xx 45g = 5.0g " clockwise"`
Question 8
The diagram shows a ball of weight W hanging in equilibrium from a string.

The string is at an angle `theta` to the vertical. The tension in the string is T. The ball is held away from the wall by a horizontal force P from a metal rod. Which relationship between the magnitudes of T, P and W is correct?
A. `P = T xx cos(theta) and W = T xx sin(theta)`.
B. `T = P + W`.
C. `T^2 = P^2 + W^2`.
D. `W = P xx tan(theta) and W = T xx cos(theta)`.
Answer: C
There are three forces acting on the ball:
Tension in the string, acting up and to the left, at an angle θ to the vertical.
Weight W, acting vertically downward.
Force P from the rod, acting horizontally to the right.
Vertical component of T: `T_y = T xx cos(theta)`
Horizontal component of T: `T_x = T xx sin(theta)`
Vertical equilibrium: `T xx cos(theta) = W`
Horizontal equilibrium: `T xx sin(theta) = P`
Because `T_y` is perpendicular to `T_x`
Hence, `T^2=T_x^2+T_y^2`
`T^2 = P^2 + W^2`.
Question 9
A uniform rod AB is attached to a vertical wall at A. The rod is held horizontally by a string attached at B and to point C, as shown in figure.

The angle between the rod and the string at B is 50°. The rod has length 1.2 m and weight 8.5 N. An object O of mass M is hung from the rod at B. The tension T in the string is 30 N.
a. Use the resolution of forces to calculate the vertical component of T.
b. State the principle of moments.
c. Use the principle of moments and take moments about A to show that the weight of the object O is 19 N.
a.
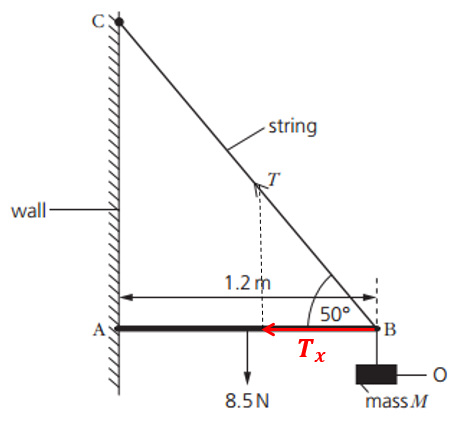
Vertical component of T:
`T_y = 30 xx sin50^o = 30 xx 0.766 = "23 N"`
b. For a system to be in equilibrium, the sum of clockwise moments about a point must be equal to the sum of the anticlockwise moments (about the same point)
c. Anticlockwise moment = Clockwise moments
`23.0 xx 1.2 = 8.5 xx 0.6 + W xx 1.2`
`W = 22.5 / 1.2 = "18.75 N"`.
Question 10
A flower basket is hung from the end of a uniform horizontal pole which projects from a wall, as shown. The pole is supported by a cable attached to a higher point on the wall.

The pole has a mass of 10 kg; the flower basket has a mass of 14 kg. By taking moments about the right hand end of the pole, determine the value of the tension in the cable T.
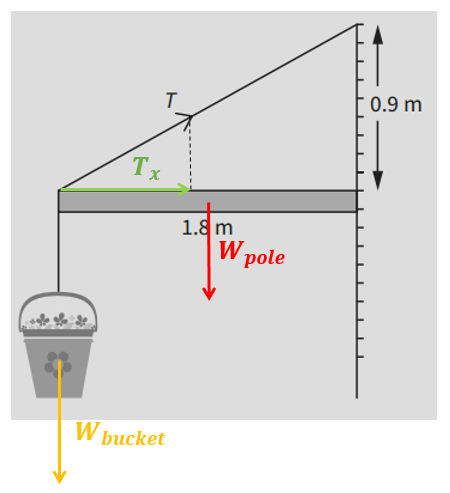
`"Angle between cable and pole" = tan^-1(0.5) = 26.6^o`.
Principle of moment:
`T xx sin(26.6) xx 1.8 = 10.0xxg xx 0.9 + 14.0xxg xx 1.8`
`T = "416 N"`
Question 1
The angle between two forces, each of magnitude 5.0 N, is 120°.

What is the magnitude of the resultant of these two forces?
Question 2
This diagram shows an object with two forces acting on it. The forces are at 90° to each other:

The diagram also shows the triangle we use to add these forces. In this case, it is sufficient to sketch the triangle.
a. Which side of the triangle represents the resultant force acting on the object?
b. Calculate the magnitude of the resultant force.
c. Use trigonometry to calculate the angle of the resultant force to the horizontal.
Question 3
A uniform metre rule is pivoted at the 34.0 cm mark, as shown.

The rule balances when a 64 g mass is hung from the 4.0 cm mark. What is the mass of the metre rule?
A. 38 g.
B. 44 g.
C. 121 g.
D. 136 g.
Question 4
A uniform beam of length L is supported by two forces X and Y so that it is in equilibrium. The position of the forces is shown in figure. What is the ratio of the forces X:Y?
What is the ratio of the forces X:Y?
Question 5
A ship is pulled at a constant speed by two small boats, A and B, as shown. The engine of the ship does not produce any force.

The tension in each cable between A and B and the ship is 4000 N. Draw a vector diagram to scale showing these three forces and use your diagram to find the value of the drag force on the ship.
Question 6
This free-body diagram shows three forces that act on a stone hanging at rest from two strings.

a. Calculate the horizontal component of the tension in each string. State why these two components are equal in magnitude?
b. Calculate the vertical component of the tension in each string.
c. Use your answer to part b to calculate the weight of the stone.
d. Draw a vector diagram of the forces on the stone. This should be a triangle of forces.
e. Use your diagram in part d to calculate the weight of the stone.
Question 7
Two children are using a long, uniform plank balanced on a cylindrical oil drum as a seesaw. The plank has a mass of 40 kg. It is 5.0 m in length and it is pivoted at a point 2.0 m from one end. Child A has a mass of 45 kg and sits at the end nearer to the pivot. Child B has a mass of 25 kg and sits at the other end.
a. Which one word in the question tells you that the plank’s centre of gravity is at its midpoint?
b. Draw a diagram to represent this situation. Show the forces acting as multiples of g, the acceleration due to gravity.
c. Determine the resultant moment acting on the plank and indicate its direction on your diagram.
Question 8
The diagram shows a ball of weight W hanging in equilibrium from a string.

The string is at an angle `theta` to the vertical. The tension in the string is T. The ball is held away from the wall by a horizontal force P from a metal rod. Which relationship between the magnitudes of T, P and W is correct?
A. `P = T xx cos(theta) and W = T xx sin(theta)`.
B. `T = P + W`.
C. `T^2 = P^2 + W^2`.
D. `W = P xx tan(theta) and W = T xx cos(theta)`.
Question 9
A uniform rod AB is attached to a vertical wall at A. The rod is held horizontally by a string attached at B and to point C, as shown in figure.

The angle between the rod and the string at B is 50°. The rod has length 1.2 m and weight 8.5 N. An object O of mass M is hung from the rod at B. The tension T in the string is 30 N.
a. Use the resolution of forces to calculate the vertical component of T.
b. State the principle of moments.
c. Use the principle of moments and take moments about A to show that the weight of the object O is 19 N.
Question 10
A flower basket is hung from the end of a uniform horizontal pole which projects from a wall, as shown. The pole is supported by a cable attached to a higher point on the wall.

The pole has a mass of 10 kg; the flower basket has a mass of 14 kg. By taking moments about the right hand end of the pole, determine the value of the tension in the cable T.