Question 1
Hydrazine reacts with oxygen.
N2H4(l) + O2(g) → N2(g) + 2H2O(l), ΔHo = −623 kJ mol−1
What is the standard enthalpy of formation of N2H4(l) in kJ mol−1? The standard enthalpy of formation of H2O(l) is –286 kJ mol−1.
A. −623 − 286
B. −623 + 572
C. −572 + 623
D. −286 + 623
Medium
Mark as Complete
Mark Scheme
Question 2
Ethanol, C2H5OH, has many industrial uses.
a. Define the term average bond enthalpy.
b. Ethanol can be used as a fuel. Determine the enthalpy of combustion of ethanol at 298K, in kJ mol−1, using the values given in section 13 of the IB Chemistry data booklet,assuming all reactants and products are gaseous.
c. Students can also measure the enthalpy of combustion of ethanol in a laboratory using calorimetry. Suggest the major source of systematic error in these procedures.
d. The standard enthalpy change of combustion, `""ΔH_c^o`, of propanoic acid is –1527 kJ mol−1. Determine the standard enthalpy change of formation of propanoic acid, in kJ mol−1, using this information and data from section 13 of the IB Chemistry data booklet.
Hard
Mark as Complete
Mark Scheme
Question 3
Consider the following equations:
2Al(s) + O2(g) → Al2O3(s), ΔHo = −1670 kJ mol−1
Mn(s) + O2(g) → MnO2(s), ΔHo = −520 kJ mol−1
What is the standard enthalpy change, in kJ mol−1, of the reaction below?
4Al(s) + 3MnO2(s) → 2Al2O3(s) + 3Mn(s)
A. –1670 + 520
B. (`frac{3}{2}`× −1670) + (3 × 520)
C. (2 × −1670) + (3 × −520)
D. (2 × −1670) − (3 × −520)
Medium
Mark as Complete
Mark Scheme
Question 4
Which ionic compound has the largest value of lattice enthalpy?
A. MgS.
B. MgO.
C. CaBr₂.
D. NaF.
Medium
Mark as Complete
Mark Scheme
Question 5
The Born–Haber cycle for the formation of magnesium oxide is shown below.
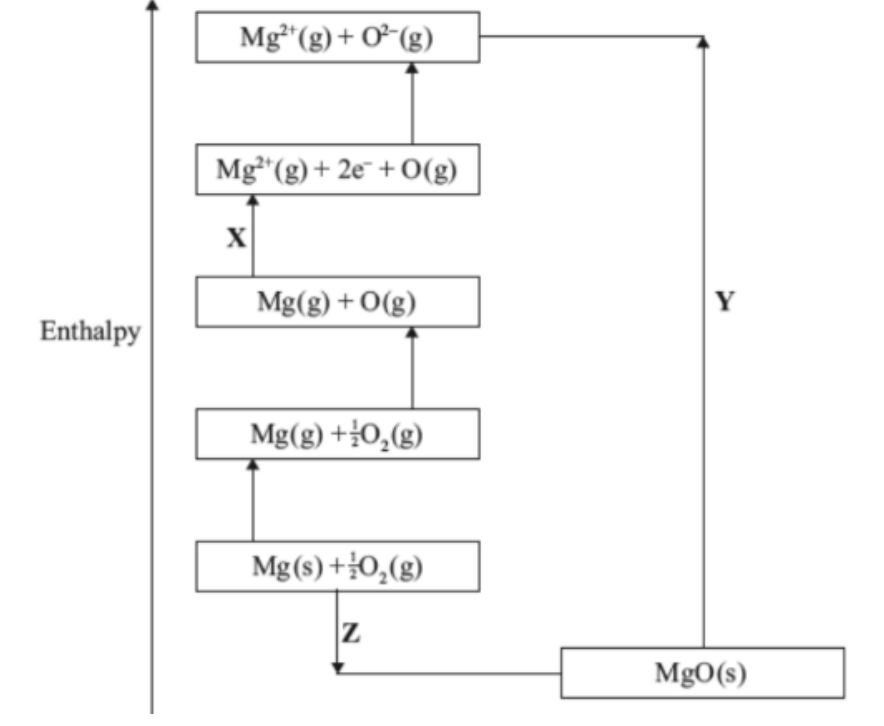
What is a correct description of the steps X, Y, and Z in this cycle?
| Step X | Step Y | Step Z |
| A. 2nd ionization energy of Mg | Enthalpy of formation of MgO | Lattice enthalpy of MgO |
| B. 2nd ionization energy of Mg | Lattice enthalpy of MgO | Enthalpy of formation of MgO |
| C. Sum of the 1st and 2nd ionization energies of Mg | Lattice enthalpy of MgO | Enthalpy of formation of MgO |
| D. Sum of 1st and 2nd ionization energies of Mg | Enthalpy of formation of MgO | Lattice enthalpy of MgO |
Medium
Mark as Complete
Mark Scheme
Question 6
a. Two chemistry students wished to determine the enthalpy of hydration of anhydrous magnesium sulfate. They measured the initial and the highest temperature reached when anhydrous magnesium sulfate, MgSO4 (s), was dissolved in water. They presented their results in this table:
| Mass of anhydrous magnesium sulfate / g | 3.01 |
| Volume of water / cm³ | 50.0 |
| Initial temperature / °C | 17.0 |
| Highest temperature / °C | 26.7 |
i. Calculate the amount, in mol, of anhydrous magnesium sulfate.
ii. Calculate the enthalpy change, ΔH1, for anhydrous magnesium sulfate dissolving in water, in kJ mol−1. State your answer to the correct number of significant figures.
b. The students repeated the experiment using 6.16 g of solid hydrated magnesium sulfate, MgSO4⋅7H2O(s), and 50 cm3 of water. They found the enthalpy change, ΔH2, to be +18 kJ mol−1. The enthalpy of hydration of solid magnesium sulfate is difficult to determine experimentally, but can be determined using the diagram below:
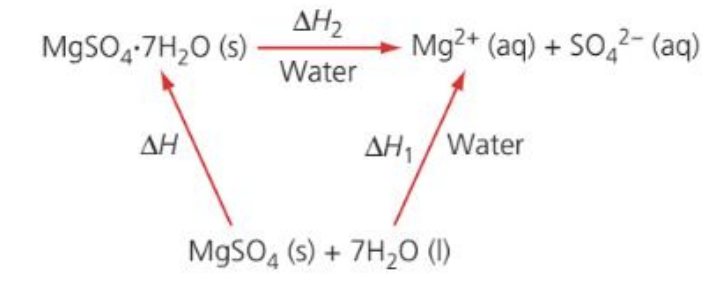
i. Determine the enthalpy change, ΔH, in kJ mol−1, for the hydration of solid anhydrous magnesium sulfate, MgSO4.
ii. The literature value for the enthalpy of hydration of anhydrous magnesium sulfate is –103 kJ mol−1. Calculate the percentage difference between the literature value and the value determined from the experimental result, giving your answer to one decimal place.
Hard
Mark as Complete
Mark Scheme
Question 7
Which value represents the lattice enthalpy, in kJ mol-1, of strontium chloride, SrCl₂?

A. −(−829) + 164 + 243 + 550 + 1064 − (−698)
B. −829 + 164 + 243 + 550 + 1064 − 698
C. −(−829) + 164 + 243 + 550 + 1064 − 698
D. −829 + 164 + 243 + 550 + 1064 − (−698)
Medium
Mark as Complete
Mark Scheme
Question 8
The Born–Haber cycle for potassium oxide is shown below:
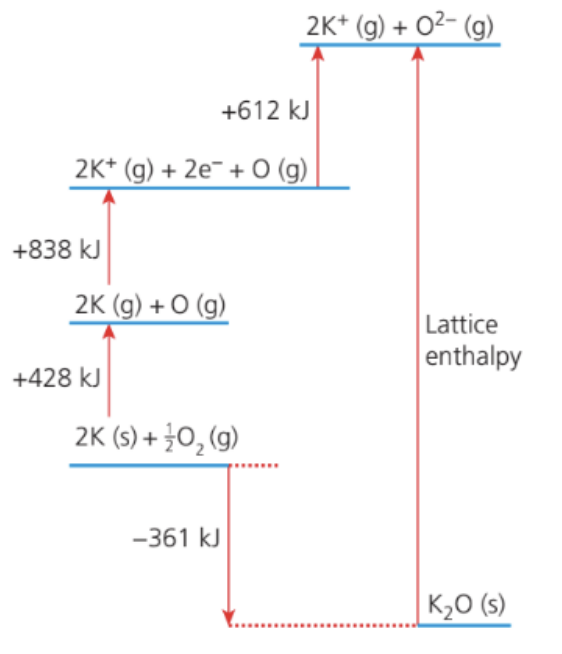
Which expression represents the lattice enthalpy, in kJ mol−1?
A. −361 + 428 + 838 + 612
B. −(−361) + 428 + 838 + 612
C. −361 + 428 + 838 − 612
D. −(−361) + 428 + 838 − 612
Medium
Mark as Complete
Mark Scheme
Question 9
What is the enthalpy change of the reaction?
C6H14(l) → C2H4(g) + C4H10(g)
| Substance | ΔHo/kJ mol−1 |
| C₆H₁₄(l) | –4163 |
| C₂H₄(g) | –1411 |
| C₄H₁₀(g) | –2878 |
A. +1411 + 2878 + 4163
B. +1411 − 2878 − 4163
C. +1411 + 2878 − 4163
D. −1411 − 2878 + 4163
Medium
Mark as Complete
Mark Scheme
Question 10
What is the enthalpy of combustion of urea, (NH2)2CO, in kJ mol−1?
CO(NH2)2(s) +`frac{3}{2}`O2(g) → CO2(g) + N2(g) + 2H2O(l)
| Substance | ΔHo/kJ mol−1 |
| CO₂(g) | –394 |
| CO(NH₂)₂(s) | –333 |
| H₂O(l) | –286 |
A. (−333) − (−394) − 2 × (−286)
B. [−394 + 2 × (−286) − `frac{3}{2}`× (−333)]
C. (−394) + 2 × (−286) + (−333)
D. (−394) + 2 × (−286) − (−333)
Medium
Mark as Complete
Mark Scheme
Question 11
What is the enthalpy change, in kJ mol⁻¹, of the following reaction? 3H2(g) + N2(g) ⇌ 2NH3(g)
| Bond | Bond enthalpy / kJ mol-1 |
| N≡N | 945 |
| H–H | 436 |
| N–H | 391 |
A.(6 × 391) − [(3 × 436) + 945]
B. (3 × 391) − (436 + 945)
C. −[(3 × 436) + 945] + (3 × 391)
D. −(6 × 391) + [(3 × 436) + 945]
Medium
Mark as Complete
Mark Scheme
Question 12
a. Define the term average bond enthalpy.
b. Use the information from Table 10 in the Data Booklet to calculate the enthalpy change for the complete combustion of but-1-ene according to the following equation.
C4H8(g) + 6O2(g) → 4CO2(g) + 4H2O(g)
c. Predict, giving a reason, how the enthalpy change for the complete combustion of but 2-ene would compare with that of but-1-ene based on average bond enthalpies.
Hard
Mark as Complete
Mark Scheme
Question 13
The standard enthalpy changes for the following reactions can be found in Table 13 of the Data Booklet:
C(s) + O2(g) → CO2(g)
H2(g) +O2(g) → H2O(l)
C8H18(l) + `12*frac{1}{2}`O2(g) → 8CO2(g) + 9H2O(l)
a. Use this information to determine the standard enthalpy change for the formation of octane from its elements.
8C(s) + 9H2(g) → C8H18(l)
b. Predict which of the following reactions has the most negative enthalpy change, and explain your choice.
I. H2(g) + `frac{1}{2}`O2(g) → H2O(g)
II. H2(g) + `frac{1}{2}`O2(g) → H2O(l)
Hard
Mark as Complete
Mark Scheme
Question 14
Two students were asked to use information from the Data Booklet to calculate a value for the enthalpy of hydrogenation of ethene to form ethane.
C2H4(g) + H2(g) → C2H6(g)
John used the average bond enthalpies from Table 10. Marit used the values of enthalpies of combustion from Table 12.
a. Calculate the value for the enthalpy of hydrogenation of ethene obtained using the average bond enthalpies given in Table 10.
b. Marit arranged the values she found in Table 12 into an energy cycle.

Calculate the value for the enthalpy of hydrogenation of ethene from the energy cycle.
c. Suggest one reason why John’s answer is slightly less accurate than Marit’s answer.
d. John then decided to determine the enthalpy of hydrogenation of cyclohexene to produce cyclohexane.
C6H10(l) + H2(g) → C6H12(l)
i. Use the average bond enthalpies to deduce a value for the enthalpy of hydrogenation of cyclohexene.
ii. The percentage difference between these two methods (average bond enthalpies and enthalpies of combustion) is greater for cyclohexene than it was for ethene. John’s hypothesis was that it would be the same. Determine why the use of average bond enthalpies is less accurate for the cyclohexene equation shown above than it was for ethene. Deduce what extra information is needed to provide a more accurate answer.
Hard
Mark as Complete
Mark Scheme
Question 15
In December 2010, researchers in Sweden announced the synthesis of N,N dinitronitramide, N(NO₂)₃. They speculated that this compound, more commonly called trinitramide, may have significant potential as an environmentally friendly rocket fuel oxidant.
a. Methanol reacts with trinitramide to form nitrogen, carbon dioxide, and water. Deduce the coefficients required to balance the equation for this reaction.
N(NO2)3(g) + CH3OH(l) → N2(g) + CO2(g) + H2O(l)
b. Suggest one reason why trinitramide might be more environmentally friendly than other rocket fuel oxidants such as ammonium perchlorate (NH₄ClO₄).
c. Calculate the enthalpy change, in kJ mol-1, when one mole of trinitramide decomposes to its elements, using bond enthalpies from section 12 of the data booklet. Assume that all the N–O bonds in this molecule have a bond enthalpy of 305 kJ mol-1.
Medium
Mark as Complete
Mark Scheme
Question 16
Methanol can be produced according to the following equation:
CO(g) + 2H2(g) → CH3OH
Calculate the standard enthalpy change of this reaction using the following data:
| Reaction | ΔH° / kJ mol-1 | |
| I. | 2CH3OH(l) + 3O2(g) → 2CO2(g) + 4H2O(l) | –1452 |
| II. | 2CO(g) + O2(g) → 2CO2(g) | –566 |
| III. | 2H2(g) + O2(g) → 2H2O(l) | –572 |
Medium
Mark as Complete
Mark Scheme
Question 17
In the gas phase, A reacts with hydrogen to form D.
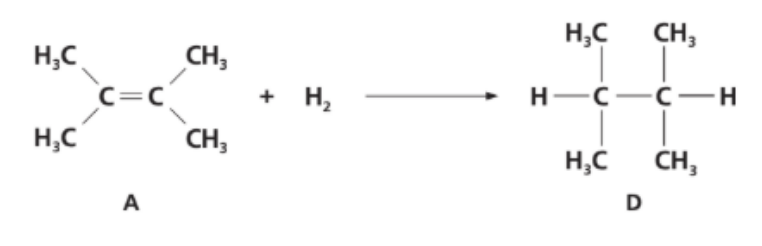
a. Use bond enthalpies given in section 12 of the IB Chemistry data booklet to determine the enthalpy change, in kJ mol-1, of the reaction. State whether the reaction is exothermic or endothermic.
b. The standard enthalpy change of combustion of A is –4000 kJ mol-1. Calculate the amount of A, in mol, that would have to be burned to raise the temperature of 1 dm³ of water from 20°C to 100°C.
Medium
Mark as Complete
Mark Scheme
Question 18
In which order does the oxygen–oxygen bond enthalpy increase?
A. H₂O₂ < O₂ < O₃
B. H₂O₂ < O₃ < O₂
C. O₂ < O₃ < H₂O₂
D. O₃ < H₂O₂ < O₂
Medium
Mark as Complete
Mark Scheme
Question 19
Which combination will give you the enthalpy change for the hydrogenation of ethene to ethane, ΔH1?
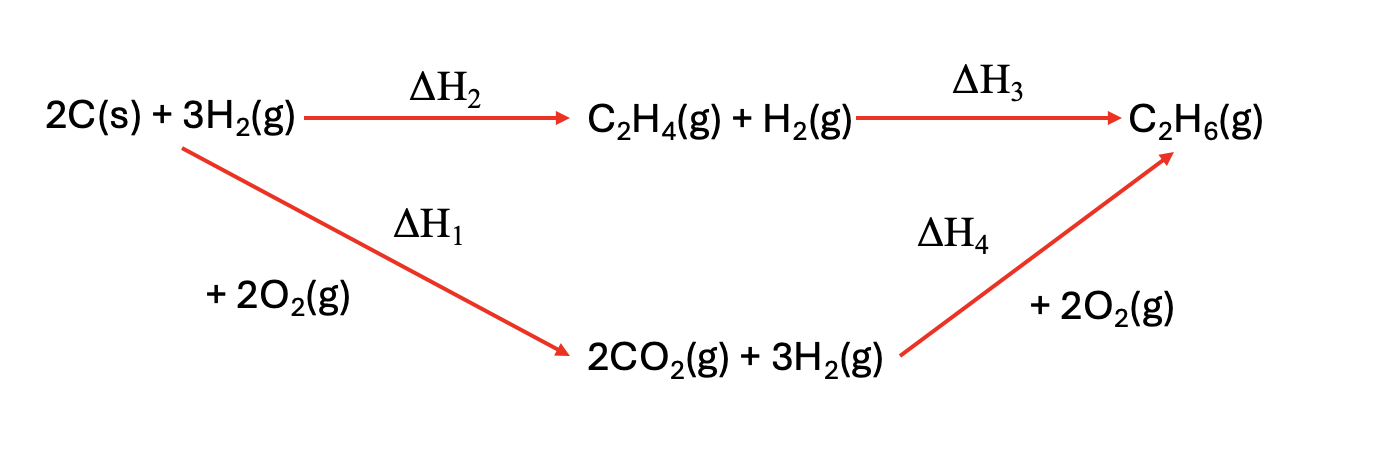
A. ΔH2 + ΔH1 - ΔH4
B. ΔH2 - ΔH4 + ΔH1
C. -ΔH2 + ΔH1 - ΔH4
D. -ΔH2 - ΔH1 + ΔH4
Medium
Mark as Complete
Mark Scheme
Question 20
The C=C bond has a bond length of 134 pm and an average bond enthalpy of 614 kJ mol⁻¹. Which values would be most likely for the C–C bond?
| Bond length / pm | Average bond enthalpy / kJ mol-1 |
| 154 | 346 |
| 154 | 780 |
| 116 | 346 |
| 116 | 780 |
A. 154 pm, 346 kJ mol-1
B. 154 pm, 780 kJ mol-1
C. 116 pm, 346 kJ mol-1
D. 116 pm, 780 kJ mol-1
Medium
Mark as Complete
Mark Scheme
Question 1
Hydrazine reacts with oxygen.
N2H4(l) + O2(g) → N2(g) + 2H2O(l), ΔHo = −623 kJ mol−1
What is the standard enthalpy of formation of N2H4(l) in kJ mol−1? The standard enthalpy of formation of H2O(l) is –286 kJ mol−1.
A. −623 − 286
B. −623 + 572
C. −572 + 623
D. −286 + 623
Answer: C. −572 + 623
Step 1: Write the enthalpy-of-formation expression
ΔHreaction = ∑ΔHf(products) − ∑ΔHf(reactants)
So:
−623 = [ΔHf(N2) + 2ΔHf(H2O)] − [ΔHf(N2H4) + ΔHf(O2)]
Since:
ΔHf(N2) = 0, ΔHf(N2) = 0
−623 = [0 + 2(−286)] − [ΔHf(N2H4)]
Step 2: Solve for ΔHf(N2H4)
−623 = −572 − ΔHf(N2H4)
ΔHf(N2H4) = −572 + 623 = +51kJ mol−1
Question 2
Ethanol, C2H5OH, has many industrial uses.
a. Define the term average bond enthalpy.
b. Ethanol can be used as a fuel. Determine the enthalpy of combustion of ethanol at 298K, in kJ mol−1, using the values given in section 13 of the IB Chemistry data booklet,assuming all reactants and products are gaseous.
c. Students can also measure the enthalpy of combustion of ethanol in a laboratory using calorimetry. Suggest the major source of systematic error in these procedures.
d. The standard enthalpy change of combustion, `""ΔH_c^o`, of propanoic acid is –1527 kJ mol−1. Determine the standard enthalpy change of formation of propanoic acid, in kJ mol−1, using this information and data from section 13 of the IB Chemistry data booklet.
a. Define average bond enthalpy
The energy required to break one mole of a given bond in the gas phase, averaged over that bond in many different molecules.
b. ΔH° for combustion of ethanol at 298 K (all species gaseous)
Reaction (gas phase):
C2H5OH(g) + 3O2(g) → 2CO2(g) + 3H2O(g)
Use standard enthalpies of formation (kJ mol−1, IB Data Booklet):
• `""ΔH_f^o`[CO2(g)] = −393.5
• `""ΔH_f^o`[H2O(g)] = −241.8
• `""ΔH_f^o`[C2H5OH(g)] ≈ −235
ΔH°comb = [2(−393.5) + 3(−241.8)] − [(−235) + 0]
= (−1512.4) − (−235) ≈ −1.28 × 103 kJ mol−1
c. Major source of systematic error in calorimetry
Heat loss to the surroundings (and to the calorimeter) during burning, so the measured ΔH is less exothermic than the true value. (Incomplete combustion is another source, but heat loss is the main systematic error.)
d. ΔHf° of propanoic acid, given `""ΔH_c^o`(C3H6O2(l)) = -1527 kJ mol−1
Combustion:
C3H6O2(l) + O2(g) → 3CO2(g) + 3H2O(l)
Data (kJ mol−1):
• `""ΔH_f^o`[CO2(g)] = −393.5
• `""ΔH_f^o`[H2O(l)] = −285.8
−1527 = [3(−393.5) + 3(−285.8)] − `""ΔH_f^o`[C3H6O2(l)]
−1527 = −2037.9 − `""ΔH_f^o`
`""ΔH_f^o` ≈ −5.11 × 102 kJ mol−1 (≈ −511 kJ mol−1)
Question 3
Consider the following equations:
2Al(s) + O2(g) → Al2O3(s), ΔHo = −1670 kJ mol−1
Mn(s) + O2(g) → MnO2(s), ΔHo = −520 kJ mol−1
What is the standard enthalpy change, in kJ mol−1, of the reaction below?
4Al(s) + 3MnO2(s) → 2Al2O3(s) + 3Mn(s)
A. –1670 + 520
B. (`frac{3}{2}`× −1670) + (3 × 520)
C. (2 × −1670) + (3 × −520)
D. (2 × −1670) − (3 × −520)
Step 1: Observe oxidation/reduction
• In the target equation, MnO₂ → Mn, so the second reaction must be reversed. Reversing changes the sign of ΔH° to +520 kJ mol⁻¹.
• The first reaction stays as written, but must be doubled because the final reaction has 4 Al and 2 Al2O3.
Step 2: Multiply and reverse equations
(1) × 2 → 4Al(s) + 3O2(g) → 2Al2O3(s)
ΔH = 2 × (−1670) = −3340 kJ
(2) reversed × 3 → 3MnO2(s) → 3Mn(s) + 3O2(g)
ΔH = 3 × (+520) = +1560 kJ
Step 3: Add them together
4Al(s) + 3O2(g) + 3MnO2(s) → 2Al2O3(s) + 3Mn(s) + 3O2(g)
→ The 3O2(g) cancels on both sides
Final reaction:
4Al(s) + 3MnO2(s) → 2Al2O3(s) + 3Mn(s)
Step 4: Add enthalpy changes
ΔH° = (2 × −1670) + (3 × +520)
Question 4
Which ionic compound has the largest value of lattice enthalpy?
A. MgS.
B. MgO.
C. CaBr₂.
D. NaF.
Answer: B. MgO.
Lattice enthalpy depends on:
U `prop``frac{Q_1Q_2}{r}`
where
• Q1,Q2 = ionic charges
• r = distance between ion centers (sum of ionic radii)
So lattice enthalpy increases when:
1. Ion charges are higher, and
2. Ions are smaller (shorter distance between them).
A. Incorrect: MgS
Ions: Mg²⁺ and S²⁻ → both have charge ±2, which gives strong electrostatic attraction. However, sulfide ion (S²⁻) is much larger than oxide (O²⁻), which increases the distance between ions and weakens the attraction. Therefore, lattice enthalpy is high but less than MgO.
B. Correct: MgO
Ions: Mg²⁺ and O²⁻ → both have ± 2 charges. Oxygen ion is smaller than sulfur ion, so ions are closer together. Strong charge + small distance = very strong electrostatic attraction. Among all given options, this combination produces the highest lattice enthalpy.
C. Incorrect: CaBr₂
Ions: Ca²⁺ and Br⁻. Cation has high charge (+2), but bromide ions are large, increasing distance. Also, there are two Br⁻ ions, but the overall electrostatic attraction per ion pair is smaller due to the large radius of Br⁻. Lattice enthalpy is therefore lower than MgO or MgS.
D. Incorrect: NaF
Ions: Na⁺ and F⁻ → both ±1 charges only. Both ions are small, so the distance is short, which helps, but the charge product (1 × 1 = 1) is much lower than that of ±2 ions (4). Hence, the overall lattice enthalpy is moderate, smaller than MgO’s.
Question 5
The Born–Haber cycle for the formation of magnesium oxide is shown below.

What is a correct description of the steps X, Y, and Z in this cycle?
| Step X | Step Y | Step Z |
| A. 2nd ionization energy of Mg | Enthalpy of formation of MgO | Lattice enthalpy of MgO |
| B. 2nd ionization energy of Mg | Lattice enthalpy of MgO | Enthalpy of formation of MgO |
| C. Sum of the 1st and 2nd ionization energies of Mg | Lattice enthalpy of MgO | Enthalpy of formation of MgO |
| D. Sum of 1st and 2nd ionization energies of Mg | Enthalpy of formation of MgO | Lattice enthalpy of MgO |
Answer: C.
Step X:
Goes from Mg(g) + O(g) → Mg2+(g) + 2e− + O(g)
→ This step involves removing two electrons from magnesium — that’s the sum of the 1st and 2nd ionization energies of Mg.
`=>` Step X = Sum of the 1st and 2nd ionization energies of Mg
Step Y:
Goes from Mg2+(g) + O2−(g) → MgO(s)
→ This is the process where gaseous ions form the solid lattice.
`=>` Step Y = Lattice enthalpy of MgO
Step Z:
Goes from Mg(s) + `frac{1}{2}`O2(g) → MgO(s)
→ This is the overall formation reaction, the enthalpy of formation of MgO.
`=>` Step Z = Enthalpy of formation of MgO
Question 6
a. Two chemistry students wished to determine the enthalpy of hydration of anhydrous magnesium sulfate. They measured the initial and the highest temperature reached when anhydrous magnesium sulfate, MgSO4 (s), was dissolved in water. They presented their results in this table:
| Mass of anhydrous magnesium sulfate / g | 3.01 |
| Volume of water / cm³ | 50.0 |
| Initial temperature / °C | 17.0 |
| Highest temperature / °C | 26.7 |
i. Calculate the amount, in mol, of anhydrous magnesium sulfate.
ii. Calculate the enthalpy change, ΔH1, for anhydrous magnesium sulfate dissolving in water, in kJ mol−1. State your answer to the correct number of significant figures.
b. The students repeated the experiment using 6.16 g of solid hydrated magnesium sulfate, MgSO4⋅7H2O(s), and 50 cm3 of water. They found the enthalpy change, ΔH2, to be +18 kJ mol−1. The enthalpy of hydration of solid magnesium sulfate is difficult to determine experimentally, but can be determined using the diagram below:

i. Determine the enthalpy change, ΔH, in kJ mol−1, for the hydration of solid anhydrous magnesium sulfate, MgSO4.
ii. The literature value for the enthalpy of hydration of anhydrous magnesium sulfate is –103 kJ mol−1. Calculate the percentage difference between the literature value and the value determined from the experimental result, giving your answer to one decimal place.
a.i. Moles of anhydrous MgSO₄
Mr(MgSO₄) = 24.3 + 32.1 + 4 × 16.0 = 120.4 g mol−1
n = `frac{3.01}{120.4}`3.01 = 2.50 × 10−2 mol
Answer: 2.50 × 10−2 mol (3 s.f.)
a.ii. Enthalpy change for dissolving anhydrous MgSO4, ΔH1
ΔT = 26.7 − 17.0 = 9.7 K
Take the mass of water = 50.0 g(density ≈ 1 g cm−3) and c = 4.18 J g−1K−1.
Heat released to the water:
q = mcΔT = 50.0 × 4.18 × 9.7 = 2.03 × 103
J = 2.03 kJ
Molar enthalpy (exothermic):
ΔH1 = `-frac{q}{n}`= `-frac{2.03}{2.50*10^(-2)}`= −81.2 kJ mol−1
Answer: ΔH1 ≈ −81 kJ mol−1 (2 s.f. from ΔT)
b.i. Enthalpy change for hydration of solid anhydrous MgSO4, ΔH
From the Hess diagram:
MgSO₄(s) + 7H₂O(l)![]() MgSO₄`*`7H₂O(s)
MgSO₄`*`7H₂O(s)
and both solids dissolve to the same ions:
ΔH1 = ΔH + ΔH2
with ΔH2 = +18 kJ mol−1.
→ ΔH = ΔH1 − ΔH2 ≈ (−81) − (+18) = −99 kJ mol−1
b.ii. % difference vs. literature value −103 kJ mol−1
%difference = `frac{∣ −99 − (−103) ∣}{103}*100 = frac{4}{103}*100`= 3.9%
Question 7
Which value represents the lattice enthalpy, in kJ mol-1, of strontium chloride, SrCl₂?

A. −(−829) + 164 + 243 + 550 + 1064 − (−698)
B. −829 + 164 + 243 + 550 + 1064 − 698
C. −(−829) + 164 + 243 + 550 + 1064 − 698
D. −829 + 164 + 243 + 550 + 1064 − (−698)
Answer: C. −(−829) + 164 + 243 + 550 + 1064 − 698
−829 = 164 + 243 + 550 + 1064 − 698 + U
U = −(−829) + 164 + 243 + 550 + 1064 − 698
Question 8
The Born–Haber cycle for potassium oxide is shown below:

Which expression represents the lattice enthalpy, in kJ mol−1?
A. −361 + 428 + 838 + 612
B. −(−361) + 428 + 838 + 612
C. −361 + 428 + 838 − 612
D. −(−361) + 428 + 838 − 612
Answer: B. −(−361) + 428 + 838 + 612
Using Hess’s Law
The formation enthalpy (−361 kJ mol−1) = sum of all steps leading to the gaseous ions plus the lattice enthalpy.
−361 = 428 + 838 + 612 + U
Rearranging for U:
U = −(−361) + 428 + 838 + 612
Question 9
What is the enthalpy change of the reaction?
C6H14(l) → C2H4(g) + C4H10(g)
| Substance | ΔHo/kJ mol−1 |
| C₆H₁₄(l) | –4163 |
| C₂H₄(g) | –1411 |
| C₄H₁₀(g) | –2878 |
A. +1411 + 2878 + 4163
B. +1411 − 2878 − 4163
C. +1411 + 2878 − 4163
D. −1411 − 2878 + 4163
Answer: C. +1411 + 2878 − 4163
Reasoning (Hess via combustions):
ΔHrxn = ΔHc(reactant) − ∑ΔHc(products) = (−4163) − [(−1411) + (−2878)]
Question 10
What is the enthalpy of combustion of urea, (NH2)2CO, in kJ mol−1?
CO(NH2)2(s) +`frac{3}{2}`O2(g) → CO2(g) + N2(g) + 2H2O(l)
| Substance | ΔHo/kJ mol−1 |
| CO₂(g) | –394 |
| CO(NH₂)₂(s) | –333 |
| H₂O(l) | –286 |
A. (−333) − (−394) − 2 × (−286)
B. [−394 + 2 × (−286) − `frac{3}{2}`× (−333)]
C. (−394) + 2 × (−286) + (−333)
D. (−394) + 2 × (−286) − (−333)
Answer: D. (−394) + 2 × (−286) − (−333)
Step 1. Formula
ΔHreaction = ∑ΔHf(products) − ∑ΔHf(reactants)
Step 2. Apply data
ΔH = [(−394) + 2(−286) + 0] − [(−333) + 0]
Question 11
What is the enthalpy change, in kJ mol⁻¹, of the following reaction? 3H2(g) + N2(g) ⇌ 2NH3(g)
| Bond | Bond enthalpy / kJ mol-1 |
| N≡N | 945 |
| H–H | 436 |
| N–H | 391 |
A.(6 × 391) − [(3 × 436) + 945]
B. (3 × 391) − (436 + 945)
C. −[(3 × 436) + 945] + (3 × 391)
D. −(6 × 391) + [(3 × 436) + 945]
Answer: A. (6 × 391) − [(3 × 436) + 945]
Step 1. Bonds broken (energy absorbed)
• 3 × H–H = 3 × 436 = 1308 kJ
• 1 × N≡N = 945 kJ
Total energy absorbed = 1308 + 945 = 2253 kJ
Step 2. Bonds formed (energy released)
Each NH₃ molecule has 3 N–H bonds, and 2 NH₃ are formed:
6 × 391 = 2346 kJ released
Step 3. Enthalpy change
ΔH = energy absorbed − energy released
ΔH = (3 × 436 + 945) − (6 × 391)
ΔH = 2253 − 2346 = −93 kJ mol−1
⇒ Correct expression:
(6 × 391) − [(3 × 436) + 945]
Question 12
a. Define the term average bond enthalpy.
b. Use the information from Table 10 in the Data Booklet to calculate the enthalpy change for the complete combustion of but-1-ene according to the following equation.
C4H8(g) + 6O2(g) → 4CO2(g) + 4H2O(g)
c. Predict, giving a reason, how the enthalpy change for the complete combustion of but 2-ene would compare with that of but-1-ene based on average bond enthalpies.
a. Define average bond enthalpy
The average bond enthalpy is the energy required to break one mole of a specified bond in gaseous molecules, averaged over that bond in many different compounds (so it’s an average value, not compound-specific).
b. ΔH for the complete combustion of but-1-ene
C4H8(g) + 6O2(g) → 4CO2(g) + 4H2O(g)
Count bonds:
• Reactants:
o But-1-ene (CH₂=CH–CH₂–CH₃): 1 × C=C, 2 × C–C, 8 × C–H
o Oxygen: 6 × O=O
• Products:
o 4 CO₂: 8 × C=O (in CO₂)
o 4 H₂O(g): 8 × O–H
Use average bond enthalpies (kJ mol-1):
C=C: 614, C–C: 348, C–H: 413, O=O: 498, C=O (in CO₂): 805, O–H: 463.
Energy broken = 1(614) + 2(348) + 8(413) + 6(498)
= 614 + 696 + 3304 + 2988 = 7602 kJ
Energy formed = 8(805) + 8(463) = 6440 + 3704 = 10144 kJ
ΔH ≈ ΣHbroken − ΣHformed = 7602 − 10144 = −2.54 × 103 kJ mol−1
c. Compare with but-2-ene
On a bond-enthalpy basis, but-2-ene has the same numbers of each bond type as but-1-ene (1 C=C, 2 C–C, 8 C–H), so the calculated combustion enthalpy would be essentially the same.
Reason: Average bond enthalpy depends on bond type and count, not on isomer arrangement. (In reality there may be a small difference, but the bond-enthalpy method will not capture it.)
Question 13
The standard enthalpy changes for the following reactions can be found in Table 13 of the Data Booklet:
C(s) + O2(g) → CO2(g)
H2(g) +O2(g) → H2O(l)
C8H18(l) + `12*frac{1}{2}`O2(g) → 8CO2(g) + 9H2O(l)
a. Use this information to determine the standard enthalpy change for the formation of octane from its elements.
8C(s) + 9H2(g) → C8H18(l)
b. Predict which of the following reactions has the most negative enthalpy change, and explain your choice.
I. H2(g) + `frac{1}{2}`O2(g) → H2O(g)
II. H2(g) + `frac{1}{2}`O2(g) → H2O(l)
a. Step 1: Write an energy cycle using Hess’s law
Formation = [combustion of elements] – [combustion of compound]
`"ΔH_f^o` = [8ΔH(C) + 9ΔH(H2)] − [ΔH(C8H18)]
Step 2: Substitute values
`"ΔH_f^o` = [8(−394) + 9(−286)] − (−5470) = [−3152 − 2574] + 5470
= −5726 + 5470 = −256 kJ mol−1
b. Predict which of the following has the most negative enthalpy change
| Reaction | Type | ΔH° (approx) |
| I | H₂(g) + `frac{1}{2}`O₂(g) → H₂O(g) | –242 kJ mol⁻¹ |
| II | H₂(g) + `frac{1}{2}`O₂(g) → H₂O(l) | –286 kJ mol⁻¹ |
Water (l) formation releases more energy because of extra hydrogen bonding/condensation energy when gas condenses to liquid.
→ Reaction II has the most negative (most exothermic) enthalpy change. (Formation of liquid water releases additional energy due to intermolecular forces.)
Question 14
Two students were asked to use information from the Data Booklet to calculate a value for the enthalpy of hydrogenation of ethene to form ethane.
C2H4(g) + H2(g) → C2H6(g)
John used the average bond enthalpies from Table 10. Marit used the values of enthalpies of combustion from Table 12.
a. Calculate the value for the enthalpy of hydrogenation of ethene obtained using the average bond enthalpies given in Table 10.
b. Marit arranged the values she found in Table 12 into an energy cycle.

Calculate the value for the enthalpy of hydrogenation of ethene from the energy cycle.
c. Suggest one reason why John’s answer is slightly less accurate than Marit’s answer.
d. John then decided to determine the enthalpy of hydrogenation of cyclohexene to produce cyclohexane.
C6H10(l) + H2(g) → C6H12(l)
i. Use the average bond enthalpies to deduce a value for the enthalpy of hydrogenation of cyclohexene.
ii. The percentage difference between these two methods (average bond enthalpies and enthalpies of combustion) is greater for cyclohexene than it was for ethene. John’s hypothesis was that it would be the same. Determine why the use of average bond enthalpies is less accurate for the cyclohexene equation shown above than it was for ethene. Deduce what extra information is needed to provide a more accurate answer.
a. Using average bond enthalpies (Table 10) for
C2H4(g) + H2(g) → C2H6(g)
Bonds broken:
1 × C=C (614) + 1 × H–H (436) = 1050 kJ mol-1
Bonds formed:
1 × C–C (348) + 2 × C–H (2×413 = 826) = 1174 kJ mol-1
ΔH = ΣHbroken − ΣHformed = 1050 − 1174 = −1.24 × 102 kJ mol−1 So the hydrogenation is exothermic (~–124 kJ mol-1).
b. Using the enthalpies of combustion (Table 12) from Marit’s cycle From the diagram (standard values):
• ΔHc (C2H4) = −1411 kJ mol−1
• ΔHc(H2) = −286 kJ mol−1
• ΔHc (C2H6) = −1560 kJ mol−1
By Hess’ law:
ΔHhydrog = [(−1411) + (−286)] − [(−1560)] = −1697 + 1560 = −1.37 × 102 kJ mol−1
c. Why John’s answer is slightly less accurate than Marit’s
Average bond enthalpies are mean gas-phase values taken over many molecules, so they ignore the actual molecular environment and states. Enthalpies of combustion are compound-specific experimental data, so they give a more accurate ΔH.
d. Hydrogenation of cyclohexene → cyclohexane
C6H10(l) + H2(g) → C6H12(l)
i. Estimate with average bond enthalpies
The reaction changes one C=C to one C–C and adds two C–H (same local change as for ethene):
ΔH ≈ −124 kJ mol−1(exothermic)
ii. Why the % difference between methods is larger here, and what extra data are needed
• Average bond enthalpies apply to gas-phase, average bonds and do not account for ring strain/conformational effects in cyclohexene/cyclohexane.
• The equation involves liquids, so using gas-phase bond enthalpies neglects intermolecular forces; you would need to add enthalpies of vaporization of cyclohexene and cyclohexane (and of H₂ if applicable) to compare properly.
• Also, the C=C bond enthalpy in a ring can differ from the average value.
Therefore: To obtain a more accurate answer, you need compound-specific thermochemical data – e.g. standard enthalpies of combustion (as in part b), or, if using bond enthalpies, the enthalpies of vaporization to convert liquids to gases and bond enthalpies specific to the cyclic double bond.
Question 15
In December 2010, researchers in Sweden announced the synthesis of N,N dinitronitramide, N(NO₂)₃. They speculated that this compound, more commonly called trinitramide, may have significant potential as an environmentally friendly rocket fuel oxidant.
a. Methanol reacts with trinitramide to form nitrogen, carbon dioxide, and water. Deduce the coefficients required to balance the equation for this reaction.
N(NO2)3(g) + CH3OH(l) → N2(g) + CO2(g) + H2O(l)
b. Suggest one reason why trinitramide might be more environmentally friendly than other rocket fuel oxidants such as ammonium perchlorate (NH₄ClO₄).
c. Calculate the enthalpy change, in kJ mol-1, when one mole of trinitramide decomposes to its elements, using bond enthalpies from section 12 of the data booklet. Assume that all the N–O bonds in this molecule have a bond enthalpy of 305 kJ mol-1.
a. Balance the reaction with methanol
Let
aN(NO2)3(g) + bCH3OH(l) → cN2(g) + dCO2(g) + eH2O(l)
Atom balances give:
N: 4a = 2c ⇒ c = 2a
C: b = d
H: 4b = 2e ⇒ e = 2b
O: 6a + b = 2d + e = 2b + 2b = 4b ⇒ b = 2a
Choose a = 1:
N(NO2)3(g) + 2CH3OH(l) → 2N2(g) + 2CO2(g) + 4H2O(l)
b. Why trinitramide may be more environmentally friendly than ammonium perchlorate
• Combustion of trinitramide produces only N₂, CO₂, and H₂O (no chlorine).
• Ammonium perchlorate releases HCl/Cl-containing species, which are corrosive
and environmentally harmful (e.g., ozone depletion, acid deposition). → Trinitramide yields no chlorine-containing toxic gases.
c. Enthalpy change for decomposition of 1 mol of trinitramide to its elements Formula of trinitramide: N₄O₆
Assume all N–O bonds = 305 kJ mol⁻¹ (given).
Use IB bond enthalpies for the rest (typical values):
• N–N (single) ≈ 163 kJ mol⁻¹
• N≡N = 945 kJ mol⁻¹
• O=O = 498 kJ mol⁻¹
Bonds broken in N(NO₂)₃:
• 6 × N–O: 6 × 305 = 1830 kJ
• 3 × N–N: 3 × 163 = 489 kJ
Total broken = 2319 kJ
Question 16
Methanol can be produced according to the following equation:
CO(g) + 2H2(g) → CH3OH
Calculate the standard enthalpy change of this reaction using the following data:
| Reaction | ΔH° / kJ mol-1 | |
| I. | 2CH3OH(l) + 3O2(g) → 2CO2(g) + 4H2O(l) | –1452 |
| II. | 2CO(g) + O2(g) → 2CO2(g) | –566 |
| III. | 2H2(g) + O2(g) → 2H2O(l) | –572 |
Use Hess’ law with the given combustion enthalpies.
The idea: enthalpy of reaction = (sum of combustion enthalpies of reactants) – (combustion enthalpy of product).
From the data:
• (II) 2CO + O2 → 2CO2, ΔHo = −566 kJ
→ per 1 CO: –283 kJ
• (III) 2H2 + O2 → 2H2O(l), ΔHo = −572 kJ
→ for 2 H2: –572 kJ
• (I) 2CH3OH(l) + 3O2 → 2CO2 + 4H2O(l), ΔHo = −1452 kJ
→ per 1 CH3OH: –726 kJ
Now apply Hess:
ΔHo = [(−283) + (−572)] − [(−726)] = −855 + 726 = −129 kJ mol−1
Question 17
In the gas phase, A reacts with hydrogen to form D.

a. Use bond enthalpies given in section 12 of the IB Chemistry data booklet to determine the enthalpy change, in kJ mol-1, of the reaction. State whether the reaction is exothermic or endothermic.
b. The standard enthalpy change of combustion of A is –4000 kJ mol-1. Calculate the amount of A, in mol, that would have to be burned to raise the temperature of 1 dm³ of water from 20°C to 100°C.
a. Enthalpy change for the hydrogenation A → D
Treat it with average bond enthalpies (IB data booklet):
• Bonds broken: 1 × C=C (614), 1 × H–H (436)
ΣEbroken = 614 + 436 = 1050 kJ mol−1
• Bonds formed: 1 × C–C (348), 2 × C–H (2 × 413 = 826)
ΣEformed = 348 + 826 = 1174 kJ mol−1
ΔH = ΣEbroken − ΣEformed = 1050 − 1174 = −1.2 × 102 kJ mol−1 So the reaction is exothermic (~ –120 kJ mol⁻¹).
b. Moles of A needed to heat 1 dm³ of water from 20°C to 100°C
Heat needed for water:
q = mcΔT = (1000 g)(4.18 g−1K−1)(80 K) = 3.344 × 105 = 334.4 kJ ∘
Given ΔHcomb = (of A) = −4000 kJ mol−1
n(A) = `frac{q}{∣ ΔH_"comb" ∣}` = `frac{334.4}{4000}`= 8.4 × 10−2 mol
Question 18
In which order does the oxygen–oxygen bond enthalpy increase?
A. H₂O₂ < O₂ < O₃
B. H₂O₂ < O₃ < O₂
C. O₂ < O₃ < H₂O₂
D. O₃ < H₂O₂ < O₂
Answer: B. H₂O₂ < O₃ < O₂
| Molecule | Type of O–O bond |
| H₂O₂ | Single bond (O–O) |
| O₃ | Resonance bond (between single and double) |
| O₂ | Double bond (O=O) |
Bond enthalpy trend
⇒ Single < Resonance (1.5) < Double
Order of increasing bond enthalpy
H₂O₂ < O₃ < O₂
Question 19
Which combination will give you the enthalpy change for the hydrogenation of ethene to ethane, ΔH1?

A. ΔH2 + ΔH1 - ΔH4
B. ΔH2 - ΔH4 + ΔH1
C. -ΔH2 + ΔH1 - ΔH4
D. -ΔH2 - ΔH1 + ΔH4
Answer: C. -ΔH2 + ΔH1 - ΔH4
Use Hess’ law around the cycle.
Top path (left → right):
Use Hess’ law around the cycle.
Top path (left → right):
ΔH2 + ΔH3
Bottom path (left → bottom → right):
ΔH1 + (−ΔH4)
(We use –ΔH₄ because going from bottom to right is the reverse of the arrow labeled ΔH₄.)
Equate paths:
ΔH2 + ΔH3 = ΔH1 − ΔH4
⇒ΔH3 = −ΔH2 + ΔH1 − ΔH4
Question 20
The C=C bond has a bond length of 134 pm and an average bond enthalpy of 614 kJ mol⁻¹. Which values would be most likely for the C–C bond?
| Bond length / pm | Average bond enthalpy / kJ mol-1 |
| 154 | 346 |
| 154 | 780 |
| 116 | 346 |
| 116 | 780 |
A. 154 pm, 346 kJ mol-1
B. 154 pm, 780 kJ mol-1
C. 116 pm, 346 kJ mol-1
D. 116 pm, 780 kJ mol-1
Answer: A. 154 pm, 346 kJ mol-1
Trends in bond length and strength:
• More bonds (multiple bonds) → shorter and stronger.
• Fewer bonds (single bonds) → longer and weaker.
So for a C–C single bond, compared to C=C:
• Bond length → longer than 134 pm
• Bond enthalpy → smaller than 614 kJ mol⁻¹
| Option | Bond length / pm | Bond enthalpy / kJ mol-1 | Matches trend? |
| A. Correct | 154 | 346 | Longer and weaker → fits perfectly |
| B. Incorrect | 154 | 780 | Stronger than C=C — impossible |
| C. Incorrect | 116 | 346 | Shorter but weaker — inconsistent |
| D. Incorrect | 116 | 780 | Shorter and stronger — fits triple bond, not single |
Question 1
Hydrazine reacts with oxygen.
N2H4(l) + O2(g) → N2(g) + 2H2O(l), ΔHo = −623 kJ mol−1
What is the standard enthalpy of formation of N2H4(l) in kJ mol−1? The standard enthalpy of formation of H2O(l) is –286 kJ mol−1.
A. −623 − 286
B. −623 + 572
C. −572 + 623
D. −286 + 623
Question 2
Ethanol, C2H5OH, has many industrial uses.
a. Define the term average bond enthalpy.
b. Ethanol can be used as a fuel. Determine the enthalpy of combustion of ethanol at 298K, in kJ mol−1, using the values given in section 13 of the IB Chemistry data booklet,assuming all reactants and products are gaseous.
c. Students can also measure the enthalpy of combustion of ethanol in a laboratory using calorimetry. Suggest the major source of systematic error in these procedures.
d. The standard enthalpy change of combustion, `""ΔH_c^o`, of propanoic acid is –1527 kJ mol−1. Determine the standard enthalpy change of formation of propanoic acid, in kJ mol−1, using this information and data from section 13 of the IB Chemistry data booklet.
Question 3
Consider the following equations:
2Al(s) + O2(g) → Al2O3(s), ΔHo = −1670 kJ mol−1
Mn(s) + O2(g) → MnO2(s), ΔHo = −520 kJ mol−1
What is the standard enthalpy change, in kJ mol−1, of the reaction below?
4Al(s) + 3MnO2(s) → 2Al2O3(s) + 3Mn(s)
A. –1670 + 520
B. (`frac{3}{2}`× −1670) + (3 × 520)
C. (2 × −1670) + (3 × −520)
D. (2 × −1670) − (3 × −520)
Question 4
Which ionic compound has the largest value of lattice enthalpy?
A. MgS.
B. MgO.
C. CaBr₂.
D. NaF.
Question 5
The Born–Haber cycle for the formation of magnesium oxide is shown below.

What is a correct description of the steps X, Y, and Z in this cycle?
| Step X | Step Y | Step Z |
| A. 2nd ionization energy of Mg | Enthalpy of formation of MgO | Lattice enthalpy of MgO |
| B. 2nd ionization energy of Mg | Lattice enthalpy of MgO | Enthalpy of formation of MgO |
| C. Sum of the 1st and 2nd ionization energies of Mg | Lattice enthalpy of MgO | Enthalpy of formation of MgO |
| D. Sum of 1st and 2nd ionization energies of Mg | Enthalpy of formation of MgO | Lattice enthalpy of MgO |
Question 6
a. Two chemistry students wished to determine the enthalpy of hydration of anhydrous magnesium sulfate. They measured the initial and the highest temperature reached when anhydrous magnesium sulfate, MgSO4 (s), was dissolved in water. They presented their results in this table:
| Mass of anhydrous magnesium sulfate / g | 3.01 |
| Volume of water / cm³ | 50.0 |
| Initial temperature / °C | 17.0 |
| Highest temperature / °C | 26.7 |
i. Calculate the amount, in mol, of anhydrous magnesium sulfate.
ii. Calculate the enthalpy change, ΔH1, for anhydrous magnesium sulfate dissolving in water, in kJ mol−1. State your answer to the correct number of significant figures.
b. The students repeated the experiment using 6.16 g of solid hydrated magnesium sulfate, MgSO4⋅7H2O(s), and 50 cm3 of water. They found the enthalpy change, ΔH2, to be +18 kJ mol−1. The enthalpy of hydration of solid magnesium sulfate is difficult to determine experimentally, but can be determined using the diagram below:

i. Determine the enthalpy change, ΔH, in kJ mol−1, for the hydration of solid anhydrous magnesium sulfate, MgSO4.
ii. The literature value for the enthalpy of hydration of anhydrous magnesium sulfate is –103 kJ mol−1. Calculate the percentage difference between the literature value and the value determined from the experimental result, giving your answer to one decimal place.
Question 7
Which value represents the lattice enthalpy, in kJ mol-1, of strontium chloride, SrCl₂?

A. −(−829) + 164 + 243 + 550 + 1064 − (−698)
B. −829 + 164 + 243 + 550 + 1064 − 698
C. −(−829) + 164 + 243 + 550 + 1064 − 698
D. −829 + 164 + 243 + 550 + 1064 − (−698)
Question 8
The Born–Haber cycle for potassium oxide is shown below:

Which expression represents the lattice enthalpy, in kJ mol−1?
A. −361 + 428 + 838 + 612
B. −(−361) + 428 + 838 + 612
C. −361 + 428 + 838 − 612
D. −(−361) + 428 + 838 − 612
Question 9
What is the enthalpy change of the reaction?
C6H14(l) → C2H4(g) + C4H10(g)
| Substance | ΔHo/kJ mol−1 |
| C₆H₁₄(l) | –4163 |
| C₂H₄(g) | –1411 |
| C₄H₁₀(g) | –2878 |
A. +1411 + 2878 + 4163
B. +1411 − 2878 − 4163
C. +1411 + 2878 − 4163
D. −1411 − 2878 + 4163
Question 10
What is the enthalpy of combustion of urea, (NH2)2CO, in kJ mol−1?
CO(NH2)2(s) +`frac{3}{2}`O2(g) → CO2(g) + N2(g) + 2H2O(l)
| Substance | ΔHo/kJ mol−1 |
| CO₂(g) | –394 |
| CO(NH₂)₂(s) | –333 |
| H₂O(l) | –286 |
A. (−333) − (−394) − 2 × (−286)
B. [−394 + 2 × (−286) − `frac{3}{2}`× (−333)]
C. (−394) + 2 × (−286) + (−333)
D. (−394) + 2 × (−286) − (−333)
Question 11
What is the enthalpy change, in kJ mol⁻¹, of the following reaction? 3H2(g) + N2(g) ⇌ 2NH3(g)
| Bond | Bond enthalpy / kJ mol-1 |
| N≡N | 945 |
| H–H | 436 |
| N–H | 391 |
A.(6 × 391) − [(3 × 436) + 945]
B. (3 × 391) − (436 + 945)
C. −[(3 × 436) + 945] + (3 × 391)
D. −(6 × 391) + [(3 × 436) + 945]
Question 12
a. Define the term average bond enthalpy.
b. Use the information from Table 10 in the Data Booklet to calculate the enthalpy change for the complete combustion of but-1-ene according to the following equation.
C4H8(g) + 6O2(g) → 4CO2(g) + 4H2O(g)
c. Predict, giving a reason, how the enthalpy change for the complete combustion of but 2-ene would compare with that of but-1-ene based on average bond enthalpies.
Question 13
The standard enthalpy changes for the following reactions can be found in Table 13 of the Data Booklet:
C(s) + O2(g) → CO2(g)
H2(g) +O2(g) → H2O(l)
C8H18(l) + `12*frac{1}{2}`O2(g) → 8CO2(g) + 9H2O(l)
a. Use this information to determine the standard enthalpy change for the formation of octane from its elements.
8C(s) + 9H2(g) → C8H18(l)
b. Predict which of the following reactions has the most negative enthalpy change, and explain your choice.
I. H2(g) + `frac{1}{2}`O2(g) → H2O(g)
II. H2(g) + `frac{1}{2}`O2(g) → H2O(l)
Question 14
Two students were asked to use information from the Data Booklet to calculate a value for the enthalpy of hydrogenation of ethene to form ethane.
C2H4(g) + H2(g) → C2H6(g)
John used the average bond enthalpies from Table 10. Marit used the values of enthalpies of combustion from Table 12.
a. Calculate the value for the enthalpy of hydrogenation of ethene obtained using the average bond enthalpies given in Table 10.
b. Marit arranged the values she found in Table 12 into an energy cycle.

Calculate the value for the enthalpy of hydrogenation of ethene from the energy cycle.
c. Suggest one reason why John’s answer is slightly less accurate than Marit’s answer.
d. John then decided to determine the enthalpy of hydrogenation of cyclohexene to produce cyclohexane.
C6H10(l) + H2(g) → C6H12(l)
i. Use the average bond enthalpies to deduce a value for the enthalpy of hydrogenation of cyclohexene.
ii. The percentage difference between these two methods (average bond enthalpies and enthalpies of combustion) is greater for cyclohexene than it was for ethene. John’s hypothesis was that it would be the same. Determine why the use of average bond enthalpies is less accurate for the cyclohexene equation shown above than it was for ethene. Deduce what extra information is needed to provide a more accurate answer.
Question 15
In December 2010, researchers in Sweden announced the synthesis of N,N dinitronitramide, N(NO₂)₃. They speculated that this compound, more commonly called trinitramide, may have significant potential as an environmentally friendly rocket fuel oxidant.
a. Methanol reacts with trinitramide to form nitrogen, carbon dioxide, and water. Deduce the coefficients required to balance the equation for this reaction.
N(NO2)3(g) + CH3OH(l) → N2(g) + CO2(g) + H2O(l)
b. Suggest one reason why trinitramide might be more environmentally friendly than other rocket fuel oxidants such as ammonium perchlorate (NH₄ClO₄).
c. Calculate the enthalpy change, in kJ mol-1, when one mole of trinitramide decomposes to its elements, using bond enthalpies from section 12 of the data booklet. Assume that all the N–O bonds in this molecule have a bond enthalpy of 305 kJ mol-1.
Question 16
Methanol can be produced according to the following equation:
CO(g) + 2H2(g) → CH3OH
Calculate the standard enthalpy change of this reaction using the following data:
| Reaction | ΔH° / kJ mol-1 | |
| I. | 2CH3OH(l) + 3O2(g) → 2CO2(g) + 4H2O(l) | –1452 |
| II. | 2CO(g) + O2(g) → 2CO2(g) | –566 |
| III. | 2H2(g) + O2(g) → 2H2O(l) | –572 |
Question 17
In the gas phase, A reacts with hydrogen to form D.

a. Use bond enthalpies given in section 12 of the IB Chemistry data booklet to determine the enthalpy change, in kJ mol-1, of the reaction. State whether the reaction is exothermic or endothermic.
b. The standard enthalpy change of combustion of A is –4000 kJ mol-1. Calculate the amount of A, in mol, that would have to be burned to raise the temperature of 1 dm³ of water from 20°C to 100°C.
Question 18
In which order does the oxygen–oxygen bond enthalpy increase?
A. H₂O₂ < O₂ < O₃
B. H₂O₂ < O₃ < O₂
C. O₂ < O₃ < H₂O₂
D. O₃ < H₂O₂ < O₂
Question 19
Which combination will give you the enthalpy change for the hydrogenation of ethene to ethane, ΔH1?

A. ΔH2 + ΔH1 - ΔH4
B. ΔH2 - ΔH4 + ΔH1
C. -ΔH2 + ΔH1 - ΔH4
D. -ΔH2 - ΔH1 + ΔH4
Question 20
The C=C bond has a bond length of 134 pm and an average bond enthalpy of 614 kJ mol⁻¹. Which values would be most likely for the C–C bond?
| Bond length / pm | Average bond enthalpy / kJ mol-1 |
| 154 | 346 |
| 154 | 780 |
| 116 | 346 |
| 116 | 780 |
A. 154 pm, 346 kJ mol-1
B. 154 pm, 780 kJ mol-1
C. 116 pm, 346 kJ mol-1
D. 116 pm, 780 kJ mol-1