Question 1
Portable telephones are first sold in the country Cellmania in 1990. During 1990, the number of units sold is 160 . In 1991, the number of units sold is 240 and in 1992, the number of units sold is 360 .
In 1993 it was noticed that the annual sales formed a geometric sequence with first term 160 , the 2nd and 3rd terms being 240 and 360 respectively.
(a) What is the common ratio of this sequence? Assume that this trend in sales continues.
(b) How many units will be sold during 2002 ?
(c) In what year does the number of units sold first exceed 5000 ? Between 1990 and 1992, the total number of units sold is 760 .
(d) What is the total number of units sold between 1990 and 2002 ? During this period, the total population of Cellmania remains approximately 80 000 .
(e) Use this information to suggest a reason why the geometric growth in sales would not continue.
Mark as Complete
Mark Scheme
Question 2
Gwendolyn added the multiples of 3, from 3 to 3750 and found that
3 + 6 + 9 +... + 3750 = s.
Calculate s.
Mark as Complete
Mark Scheme
Question 3
The following table shows four series of numbers. One of these series is geometric, one of the series is arithmetic and the other two are neither geometric nor arithmetic.
(a) Complete the table by stating the type of series that is shown.
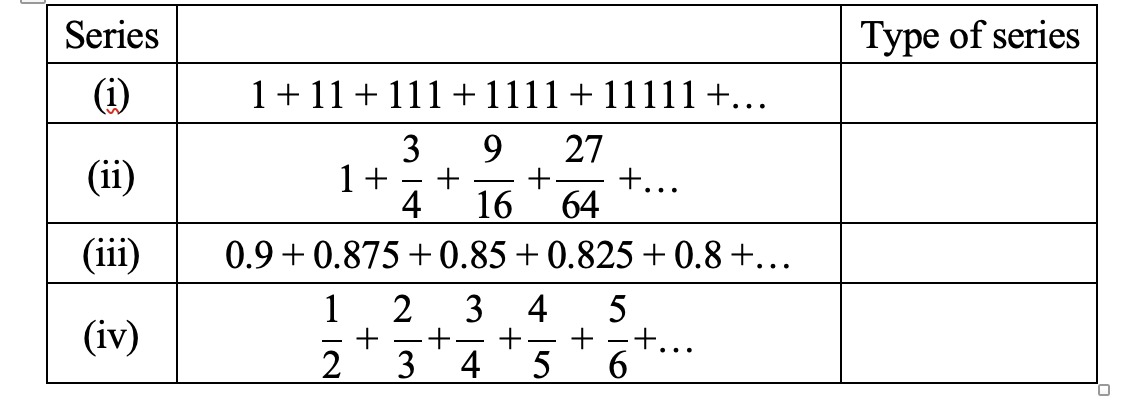
(b) The geometric series can be summed to infinity. Find this sum.
Mark as Complete
Mark Scheme
Question 4
Consider an arithmetic sequence where `u_8 = S_8 = 8.` . Find the value of the first term `u_1`, , and the value of the common difference, d.
Mark as Complete
Mark Scheme
Question 5
`\text{The } n^\text{th} \text{ term of an arithmetic sequence is given by } u_n = 15 - 3n.`
(a) `\text{State the value of the first term, } u_1.`
(b) `\text{Given that the } n^\text{th} \text{ term of this sequence is } -33, \text{ find the value of } n.`
(c) `\text{Find the common difference, } d.`
Mark as Complete
Mark Scheme
Question 6
Consider the arithmetic sequence `u_1, u_2, u_3, ...`The sum of the first terms of this sequence is given by `S_n = n^2 + 4n`
(a)
(i) Find the sum of the first five terms
(ii) Given that S6=60 , find u6
(b) Find u1
(c) Hence or otherwise, write an expression for un in terms of .
Consider a geometric sequence, vn, where `v_2 = u_1 and v_4 = u_6.`
(d) Find the possible values of the common ratio, r.
(e) Given that v99<0, find v5
Mark as Complete
Mark Scheme
Question 7
The second term of an arithmetic sequence is 10 and the fourth term is 22.
(a) Find the value of the common difference.
(b) Find an expression for un, the nth term.
Mark as Complete
Mark Scheme
Question 8
Consider the following sequence of figures.
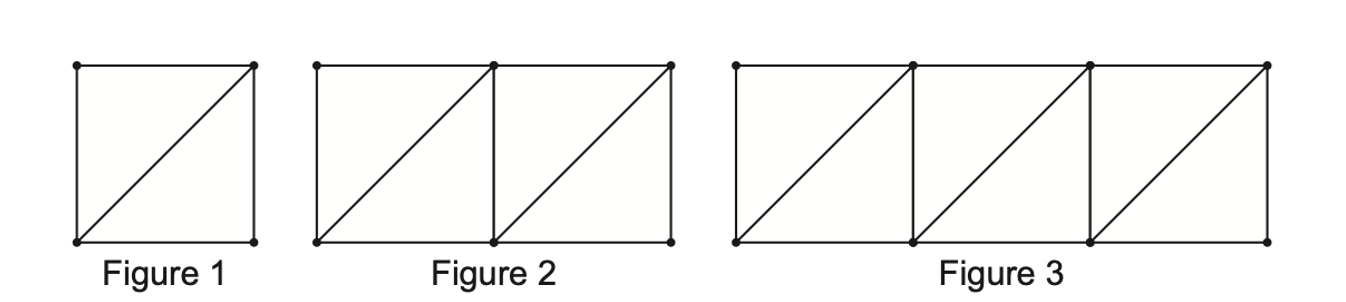
Figure 1 contains 5 line segments.
(a) Given that Figure contains line segments, show that n = 200.
(b) Find the total number of line segments in the first figures.
Mark as Complete
Mark Scheme
Question 9
In an arithmetic sequence, the first term is 8 and the second term is 5.
(a) Find the common difference.
(b) Find the tenth term.
(c) Find the sum of the first ten terms
Mark as Complete
Mark Scheme
Question 10
In an arithmetic sequence, `u_2 = 5 and u_3 = 11`
(a) Find the common difference.
(b) Find the tenth term.
(c) Find the sum of the first 20 terms.
Mark as Complete
Mark Scheme
Question 1
Portable telephones are first sold in the country Cellmania in 1990. During 1990, the number of units sold is 160 . In 1991, the number of units sold is 240 and in 1992, the number of units sold is 360 .
In 1993 it was noticed that the annual sales formed a geometric sequence with first term 160 , the 2nd and 3rd terms being 240 and 360 respectively.
(a) What is the common ratio of this sequence? Assume that this trend in sales continues.
(b) How many units will be sold during 2002 ?
(c) In what year does the number of units sold first exceed 5000 ? Between 1990 and 1992, the total number of units sold is 760 .
(d) What is the total number of units sold between 1990 and 2002 ? During this period, the total population of Cellmania remains approximately 80 000 .
(e) Use this information to suggest a reason why the geometric growth in sales would not continue.
`(a) r = 360 / 240 = 240 / 160 = 3 / 2 = 1.5`
(b) 2002 is the 13th year.
`u_13 = 160 (1.5)^(13 - 1) = 20759`(Accept 20760 or 20800)
(c) Using a gdc with `u_1 = 160, u_(k+1) = (3 / 2) u_k, u_9 = 4100, u_10 = 6150`
1999
(d) `S_13 = 160((1*5^13) -1)/(1.5 -1)`= 61958 (Accept 61960 or 62000)
(e) Sales would saturate.
Question 2
Gwendolyn added the multiples of 3, from 3 to 3750 and found that
3 + 6 + 9 +... + 3750 = s.
Calculate s.
Arithmetic sequence (may be implied)
`n = 1250 S = 1250/2(3+3750) \text{ (or } S = 1250/2(6+1249 \times 3)) = 2345625`
Question 3
The following table shows four series of numbers. One of these series is geometric, one of the series is arithmetic and the other two are neither geometric nor arithmetic.
(a) Complete the table by stating the type of series that is shown.

(b) The geometric series can be summed to infinity. Find this sum.
(a)
(i) Neither
(ii) Geometric series
(iii) Arithmetic series
(iv) Neither
(b)
(Series (ii) is a GP with a sum to infinity)
`\text{Common ratio } 3/4 S_\infty = a/(1-r) = (1/(1-3/4)) = 4`
Question 4
Consider an arithmetic sequence where `u_8 = S_8 = 8.` . Find the value of the first term `u_1`, , and the value of the common difference, d.
`4(u_1 + 8) = 8 u_1 = -6 u_1 + 7d = 8 \text{ OR } 4(2u_1 + 7d) = 8 \text{ (may be seen with their value of } u_1)`
`\text{attempt to substitute their} u_1 \text{ d}=2`
Question 5
`\text{The } n^\text{th} \text{ term of an arithmetic sequence is given by } u_n = 15 - 3n.`
(a) `\text{State the value of the first term, } u_1.`
(b) `\text{Given that the } n^\text{th} \text{ term of this sequence is } -33, \text{ find the value of } n.`
(c) `\text{Find the common difference, } d.`
`(a) u_1 = 12`
`(b) 15 - 3n = -33 n = 16``
(c) valid approach to find
`u_2 - u_1 = 9 - 12r, d = -3`
Question 6
Consider the arithmetic sequence `u_1, u_2, u_3, ...`The sum of the first terms of this sequence is given by `S_n = n^2 + 4n`
(a)
(i) Find the sum of the first five terms
(ii) Given that S6=60 , find u6
(b) Find u1
(c) Hence or otherwise, write an expression for un in terms of .
Consider a geometric sequence, vn, where `v_2 = u_1 and v_4 = u_6.`
(d) Find the possible values of the common ratio, r.
(e) Given that v99<0, find v5
(a)
(i) recognition that
`n = 5, S_5 = 45`
(ii) recognition that
`S_5 + u_6 = S_6, u_6 = 15`
(b) `60 = (6/2)(u_1 + 15) u_1 = 5`
(c) EITHER valid attempt to find (may be seen in (a) or (b)), d = 2
(d) recognition that `v_2 r^2 = v_4`
(e) recognition that r is negative `v_5 = -15sqrt(3) ( = -45/sqrt(3) )`
Question 7
The second term of an arithmetic sequence is 10 and the fourth term is 22.
(a) Find the value of the common difference.
(b) Find an expression for un, the nth term.
(a) valid method to find the common difference `d = (22 - 10) / 2`
(b) `u_1 = 10 - 6 = 4 u_n = 4 + 6 (n - 1)`
Question 8
Consider the following sequence of figures.

Figure 1 contains 5 line segments.
(a) Given that Figure contains line segments, show that n = 200.
(b) Find the total number of line segments in the first figures.
(a)
recognizing that it is an arithmetic sequence
`5, 5+4, 5+4+4, ..., d=4, u_n = u_1 + (n-1)d, 4n+1`
correct equation
`5 + 4(n - 1) = 801`
correct working (do not accept substituting n =200)
`4n - 4 = 796, n - 1 = 796/4, n = 200`
(b) recognition of sum
`S_200, u_1 + u_2 + ... + u_200, 5 + 9 + 13 + ... + 801`
correct working for AP
(200/2)(5 + 801), (200/2)(2(5) + 199(4))
80600
Question 9
In an arithmetic sequence, the first term is 8 and the second term is 5.
(a) Find the common difference.
(b) Find the tenth term.
(c) Find the sum of the first ten terms
(a) subtracting terms
`5 - 8, u_2 - u_1, d = -3`
(b) correct substitution into formula
`u_10 = 8 + (10 - 1)(-3), 8 - 27, -3(10) + 11; u_10 = -19`
(c) correct substitution into formula for sum
`S_10 = (10/2)(8 - 19), 5(2(8) + (10 - 1)(-3))`
`S_10 = -55`
Question 10
In an arithmetic sequence, `u_2 = 5 and u_3 = 11`
(a) Find the common difference.
(b) Find the tenth term.
(c) Find the sum of the first 20 terms.
(a) valid approach
`u_2 = 5, u_3 = 11 11 - 5, 11 = 5 + d, d = 6`
(b) valid approach
`u_2 - d, 5 - 6, u_1 + (3 - 1)(6) = 11; u_1 = -1`
(c) correct substitution into sum formula
`(20/2)(2(-1)+19(6)), (20/2)(-1+113); S_20 = 1120`
Question 1
Portable telephones are first sold in the country Cellmania in 1990. During 1990, the number of units sold is 160 . In 1991, the number of units sold is 240 and in 1992, the number of units sold is 360 .
In 1993 it was noticed that the annual sales formed a geometric sequence with first term 160 , the 2nd and 3rd terms being 240 and 360 respectively.
(a) What is the common ratio of this sequence? Assume that this trend in sales continues.
(b) How many units will be sold during 2002 ?
(c) In what year does the number of units sold first exceed 5000 ? Between 1990 and 1992, the total number of units sold is 760 .
(d) What is the total number of units sold between 1990 and 2002 ? During this period, the total population of Cellmania remains approximately 80 000 .
(e) Use this information to suggest a reason why the geometric growth in sales would not continue.
Question 2
Gwendolyn added the multiples of 3, from 3 to 3750 and found that
3 + 6 + 9 +... + 3750 = s.
Calculate s.
Question 3
The following table shows four series of numbers. One of these series is geometric, one of the series is arithmetic and the other two are neither geometric nor arithmetic.
(a) Complete the table by stating the type of series that is shown.

(b) The geometric series can be summed to infinity. Find this sum.
Question 4
Consider an arithmetic sequence where `u_8 = S_8 = 8.` . Find the value of the first term `u_1`, , and the value of the common difference, d.
Question 5
`\text{The } n^\text{th} \text{ term of an arithmetic sequence is given by } u_n = 15 - 3n.`
(a) `\text{State the value of the first term, } u_1.`
(b) `\text{Given that the } n^\text{th} \text{ term of this sequence is } -33, \text{ find the value of } n.`
(c) `\text{Find the common difference, } d.`
Question 6
Consider the arithmetic sequence `u_1, u_2, u_3, ...`The sum of the first terms of this sequence is given by `S_n = n^2 + 4n`
(a)
(i) Find the sum of the first five terms
(ii) Given that S6=60 , find u6
(b) Find u1
(c) Hence or otherwise, write an expression for un in terms of .
Consider a geometric sequence, vn, where `v_2 = u_1 and v_4 = u_6.`
(d) Find the possible values of the common ratio, r.
(e) Given that v99<0, find v5
Question 7
The second term of an arithmetic sequence is 10 and the fourth term is 22.
(a) Find the value of the common difference.
(b) Find an expression for un, the nth term.
Question 8
Consider the following sequence of figures.

Figure 1 contains 5 line segments.
(a) Given that Figure contains line segments, show that n = 200.
(b) Find the total number of line segments in the first figures.
Question 9
In an arithmetic sequence, the first term is 8 and the second term is 5.
(a) Find the common difference.
(b) Find the tenth term.
(c) Find the sum of the first ten terms
Question 10
In an arithmetic sequence, `u_2 = 5 and u_3 = 11`
(a) Find the common difference.
(b) Find the tenth term.
(c) Find the sum of the first 20 terms.