2.1 Straight Lines

A student has drawn the two straight line graphs `L_1`and `L_2`and marked in the angle between them as a right angle, as shown below. The student has drawn one of the lines incorrectly.

Consider `L_1` with equation  `y=2x+2`and `L_2`with equation `y=-1/4x+1`

(a) Write down the gradients of `L_1` and `L_2` using the given equations.

(b) Which of the two lines has the student drawn incorrectly?

(c) How can you tell from the answer to part (a) that the angle between `L_1` and `L_2` should not be `90^o`?

(d) Draw the correct version of the incorrectly drawn line on the diagram.

(a) `L_1` has gradient 2 and `L_2`has gradient `-1/4`

(b) `L_2` is drawn incorrectly.

(c) The product of the gradients is `2xx-1/4=-1/2!=-1`

(d) The drawing should show a straight line passing through `x` and `y` intercepts at `(4,0)` and `(0,1)`  respectively.

(a) On the grid above, draw a straight line with a gradient of `-3`that passes through the point `(-2,0)`.

(b) Find the equation of this line

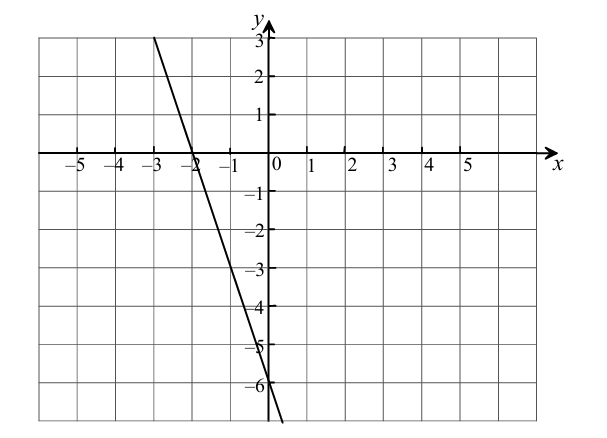
(a) line passes through `(-2,0)`

      line is straight
   negative gradient (line must be straight for mark to be awarded)
   correct gradient (line must be straight for mark to be awarded)

(b) `y-0=-3(x+2)` or `3x+y=3(-2)+1(0)` or `y=-3x+c` etc

      `3x+y=-6`  (or equivalent) 

(a) Write down the gradient of the line `y=3x+4.`

(b) Find the gradient of the line which is perpendicular to the line `y=3x+4.`

(c) Find the equation of the line which is perpendicular to `y=3x+4`and which passes through the point `(6,7)`.

(d) Find the coordinates of the point of intersection of these two lines.

(a) `3`

(b) `-1/3` (ft) from (a)

(c) Substituting `(6,7)` in `y="their " mx+c`or equivalent to find `c`.

                                         `y=-1/3 x+9`  `"or equivalent"`

(d) `(1.5,8.5)`

A straight line, `L_1`, has equation `x+4y+34=0`

(a) Find the gradient of `L_1`

     The equation of line `L_2`is `y=mx`. `L_2`is perpendicular to `L_1`.

(b) Find the value of `m`.

(c) Find the coordinates of the point of intersection of the lines `L_1`and `L_2`.

(a) `4y=-x-34`or similar rearrangement
      Gradient `=-1/4`

(b) `m=4`

(c) Reasonable attempt to solve equations simultaneously

     `(-2,-8)`

     Accept `x=-2 y=-8`

A and B are points on a straight line as shown on the graph below.

(a) Write down the `y`-intercept of the line AB.

(b) Calculate the gradient of the line AB.

     The acute angle between the line AB and the `x`-axis is `theta`.

(c) Show `theta` on the diagram.

(d) Calculate the size of `theta`.

(a) `6`

(b) `((2-5))/((8-2))`

(c) Angle clearly identified.

(d) `tanθ=1/2`(or equivalent fraction)

     `theta =〖26.6〗^∘`

Line `L`has a `y`-intercept at `(0,3)`and an `x`-intercept at `(4,0)`, as shown on the following diagram.

(a) (i) Find the gradient of `L`

     (ii) Write down the equation of `L`in the form `y=mx+c`.

Line `N` is perpendicular to `L`, and passes through point `P (2,1)`.

(b) (i) Write down the gradient of `N`

     (ii) Find the equation of `N`in the form `y=mx+c`.

(a) (i) `-3/4`

     (ii) `y=-3/4 x+3`

(b) (i) `4/3`

     (ii) `1=4/3×2+c`

          `y=4/3 x-5/3`

The straight line with equation `y=3/4 x`makes an acute angle `theta`with the `x`-axis

(a) Write down the value of  `tantheta`

(b) Find the value of

     (i) `sin 2theta`

     (ii) `cos 2theta`

(a) `tantheta = 3/4`(do not accept `3/4x)`

(b) (i) `sintheta= 3/5`,      `costheta=4/5`

      correct substitution

      `e.g. sin2theta = 2(3/5)(4/5)`

      `sin2theta = 24/25`

      (ii) correct substitution

      `e.g. cos2theta=1-2(3/5)^2`,     `(4/5)^2-(3/5)^2`

      `cos2theta=7/25`

A rocket moving in a straight line has velocity `v`km `s^-1`and displacement `s`km at time `t`seconds.
The velocity `v`is given by `v(t)=6e^(2t)+t`

When `t=0`, `s=10`.

Find an expression for the displacement of the rocket in terms of `t`.

evidence of antidifferentiation

`eg int(6e^(2t)+t`

`s=3e^(2t)+t^2/2+c`

attempt to substitute `(0,10)`into their integrated expression (even if `C`is missing)

correct working

`eg` `10=3+c`  ,   `C=7`

`s=3e^(2t)+t^2/2+7`

The line `L`is parallel to the vector `((3),(2)).`

(a) Find the gradient of the line `L.`

     The line `L`passes through the point `(9,4)`

(b) Find the equation of the line `L`in the form `y=ax+b.`

(c) Write down a vector equation for the line `L`.

(a) attempt to find gradient

 `eg`reference to change in `x`is `3`and/or `y`is `2, 3/2`

`"gradient" =2/3`

(b) attempt to substitute coordinates and/or gradient into Cartesian equation for a line

 `eg` `y-4=m(x-9),`     `y=2/3 x+b,`      `9=a(4)+c`

correct substitution

`eg` `4=2/3(9)+c`,    `y-4=2/3(x-9)`

`y=2/3 x-2``("accept " a=2/3, b=-2)`

(c) any correct equation in the form `r=a+tb`(any parameter for `t`), where `a`indicates position eg `((9),(4))` or `((0),(-2))`, and `b` is a scalar multiple of `((3),(2))`.

eg r`=((9),(4))+t((3),(2))`   ,   `((x),(y))=((3t+9),(2t+4))`  ,   r`=0i-2j+s(3i+2j)`

The graph of the function `y=f(x)`passes through the point `(3/2,4).`The gradient function of `f`is given as `f^' (x)=sin(2x-3).`Find `f(x).`

evidence of integration
e.g. `f(x)=∫sin(2x-3) dx`

`=-1/2 cos(2x-3)+C`

substituting initial condition into their expression (even if `C` is missing)

e.g. `4=-1/2 cos0+C`

       `C=4.5`

`f(x)=-1/2 cos(2x-3)+4.5`