Question 1
Consider a triangle ABC, where AC = 12, CB = 7, and `hat (BAC) = 25^@`.
Find the smallest possible perimeter of triangle ABC.
Mark as Complete
Mark Scheme
Question 2
A farmer is placing posts at points A, B, and C in the ground to mark the boundaries of a triangular piece of land on his property.
From point A, he walks due west 230 metres to point B.
From point B, he walks 175 metres on a bearing of `063^@` to reach point C.
This is shown in the following diagram.
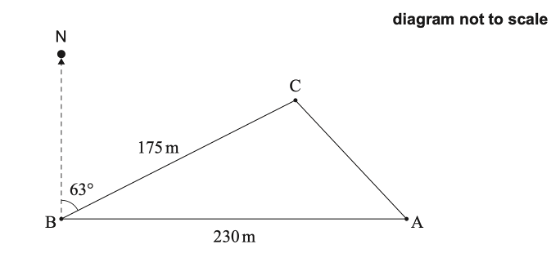
(a) Find the distance from point A to point C.
(b) Find the area of this piece of land.
(c) Find `hat (CAB)`.
The farmer wants to divide the piece of land into two sections. He will put a post at point D, which is between A and C. He wants the boundary BD to divide the piece of land such that the sections have equal area. This is shown in the following diagram.
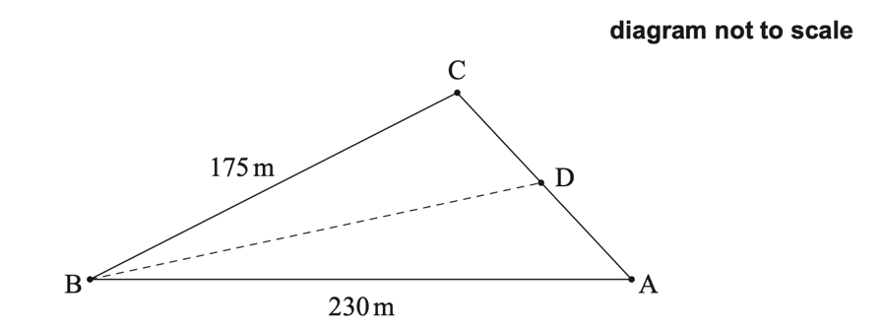
(d) Find the distance from point B to point D.
Mark as Complete
Mark Scheme
Question 3
The following diagram shows triangle ABC, with `AC=24`, `BC=17`, and `hat(ABC)=113^@`.
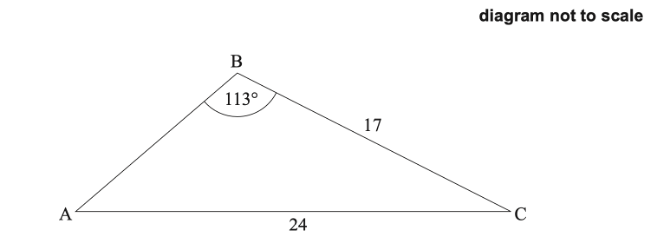
(a) Find `hat (BAC)`.
(b) Find AB.
Mark as Complete
Mark Scheme
Question 4
Jason sails his boat from point A for a distance of 100 km, on a bearing of `112^@`, to arrive at point B. He then sails on a bearing of `041^@` to point C. Jason’s journey is shown in the diagram.
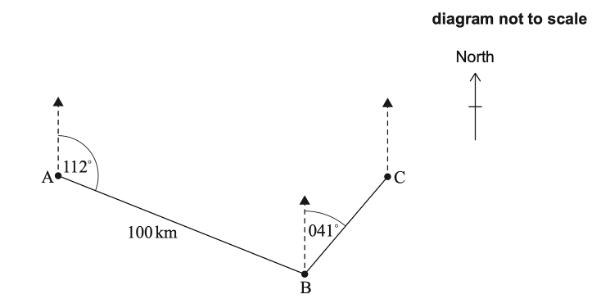
(a) Find `hat(ABC)`.
Point C is directly east of point A.
(b) Calculate the distance that Jason sails to return directly from point C to point A.
Mark as Complete
Mark Scheme
Question 5
Ruhi buys a scoop of ice cream in the shape of a sphere with a radius of 3.4 cm. The ice cream is served in a cone, and it may be assumed that `1/5` of the volume of the ice cream is inside the cone. This is shown in the following diagram.
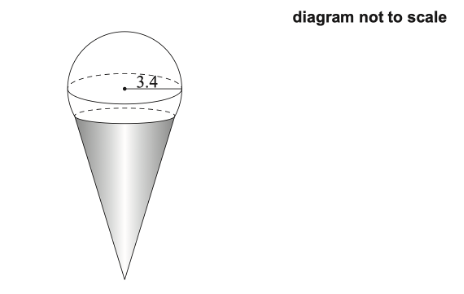
(a) Calculate the volume of ice cream that is not inside the cone.
The cone has a slant height of 11 cm and a radius of 3 cm.
The outside of the cone is covered with chocolate.
(b) Calculate the surface area of the cone that is covered with chocolate. Give your answer correct to the nearest cm2.
Mark as Complete
Mark Scheme
Question 6
The following diagram shows triangle ABC, with `AB=10, BC=x` and `AC=2x`.
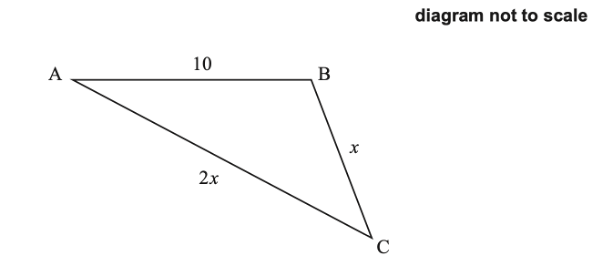
Given that `cos hat C = 3/4`, find the area of the triangle.
Give your answer in the form `(p sqrt q)/2`, where `p,q in ZZ^+`.
Mark as Complete
Mark Scheme
Question 7
In the following triangle ABC, `AB = sqrt 6` cm, `AC=10` cm and `cos hat (BAC)=1/5`.
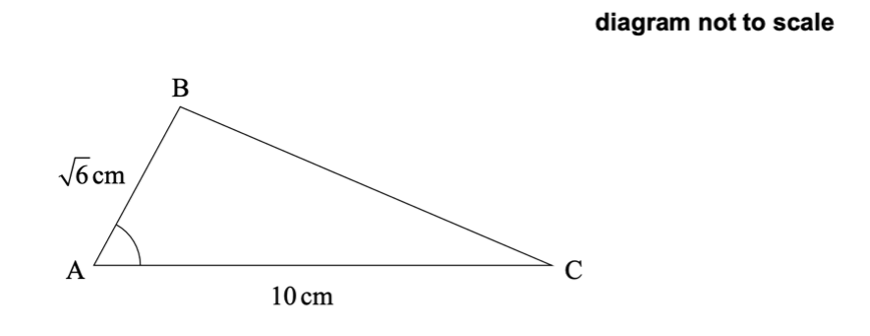
Find the area of triangle ABC.
Mark as Complete
Mark Scheme
Question 8
The following diagram shows a triangle ABC.
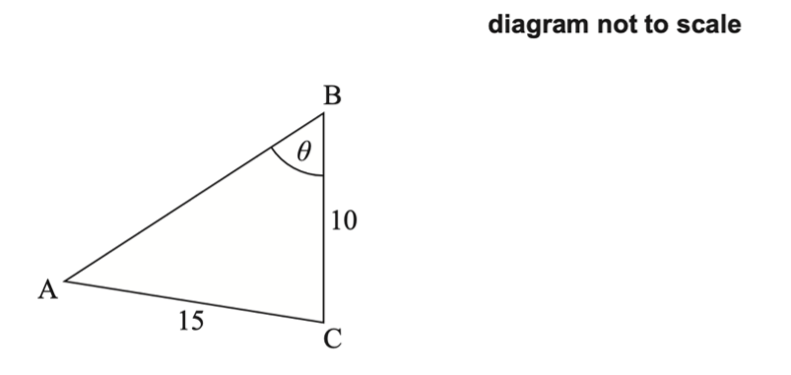
`AC = 15` cm, `BC = 10` cm, and `hat (ABC) = theta`.
Let `sin hat(CAB)=sqrt 3 / 3`.
(a) Given that `hat (ABC)` is acute, find `sin theta`.
(b) Find `cos (2 times hat (CAB))`.
Mark as Complete
Mark Scheme
Question 9
The following diagram shows a right triangle ABC. Point D lies on AB such that CD bisects `hat (ACB)`.
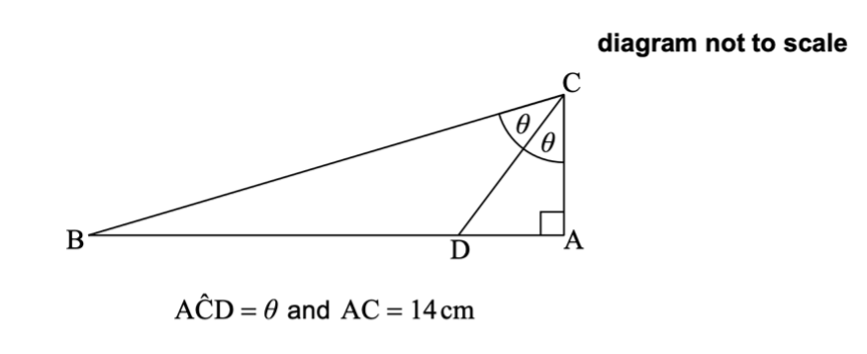
(a) Given that `sin theta = 3/5`, find the value of `cos theta`.
(b) Find the value of `cos 2 theta`.
(c) Hence or otherwise, find BC.
Mark as Complete
Mark Scheme
Question 10
The following diagram shows triangle ABC, with `AB=3` cm, `BC=8` cm, and `hat(ABC)=pi/3`.
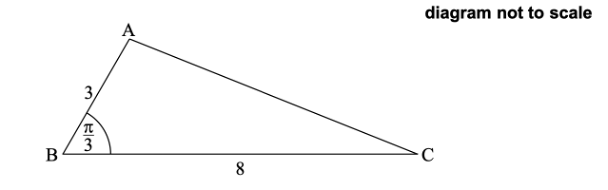
(a) Show that `AC=7` cm.
(b) The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.
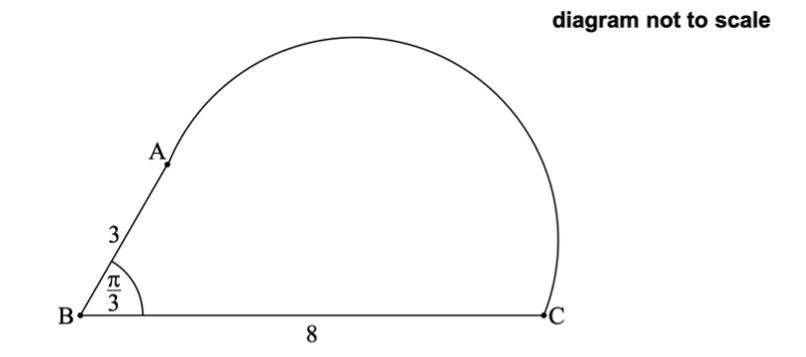
Find the exact perimeter of this shape.
Mark as Complete
Mark Scheme
Question 1
Consider a triangle ABC, where AC = 12, CB = 7, and `hat (BAC) = 25^@`.
Find the smallest possible perimeter of triangle ABC.
attempt to use cosine rule
`12^2+AB^2-2 times 12 times cos 25^@ times AB = 7^2` OR `AB^2 - 21.7513...times AB+ 95=0`
at least one correct value for AB
`AB = 6.05068...` OR `AB = 15.7007...`
using their smaller value for AB to find minimum perimeter
`12+7+6.05068...`
`25.0506 ...`
minimum perimeter `= 25.1`.
Question 2
A farmer is placing posts at points A, B, and C in the ground to mark the boundaries of a triangular piece of land on his property.
From point A, he walks due west 230 metres to point B.
From point B, he walks 175 metres on a bearing of `063^@` to reach point C.
This is shown in the following diagram.

(a) Find the distance from point A to point C.
(b) Find the area of this piece of land.
(c) Find `hat (CAB)`.
The farmer wants to divide the piece of land into two sections. He will put a post at point D, which is between A and C. He wants the boundary BD to divide the piece of land such that the sections have equal area. This is shown in the following diagram.

(d) Find the distance from point B to point D.
(a) `hat(ABC) = 27^@`
attempt to substitute into cosine rule
`175^2 + 230^2 - 2(175)(230) cos 27^@`
`108.62308 ...`
`AC = 109` (m)
(b) correct substitution into area formula
`1/2 xx 175 xx 230 xx sin 27^@`
`9136.55 ...`
area `= 9140 \ (m^2)`
(c) attempt to substitute into sine rule or cosine rule
`(sin 27^@) / (108.623...) = (sin hat A) / 175` OR `cos A = ((108.623...)^2 + 230^2 - 175^2) / (2 xx 108.623... xx 230)`
`47.0049...`
`hat(CAB)=47.0^@`
(d) recognizing that for areas to be equal, AD = DC
`AD = 1/2 AC = 54.3115 ...`
attempt to substitute into cosine rule to find BD
correct substitution into cosine rule
`BD^2=230^2 +54.3115^2 − 2(230)(54.3115) cos 47.0049^@`
`BD = 197.009...`
`BD=197` (m)
Question 3
The following diagram shows triangle ABC, with `AC=24`, `BC=17`, and `hat(ABC)=113^@`.

(a) Find `hat (BAC)`.
(b) Find AB.
(a) attempt to use sine rule
`24 / (sin 113^@) = 17 / (sin hat(BAC))` OR `sin hat(BAC) = 0.652024 ...`
`40.6943 ...`
`hat (BAC)=40.7^@`
(b) attempt to use cosine rule
correct substitution
`AB^2 = 17^2 + 24^2 - 2 xx 17 xx 24 xx cos 26.3056 ... ^@` OR `AB^2 = 133.502 ...`
`11.5543 ...`
`AB=11.6`
Question 4
Jason sails his boat from point A for a distance of 100 km, on a bearing of `112^@`, to arrive at point B. He then sails on a bearing of `041^@` to point C. Jason’s journey is shown in the diagram.

(a) Find `hat(ABC)`.
Point C is directly east of point A.
(b) Calculate the distance that Jason sails to return directly from point C to point A.
(a) recognizing supplementary angles or acute angles in right-triangles
`hat(ABC) = 41^@ + (180^@ - 112^@), 41^@ + (90^@ - 22^@)`
`hat(ABC) = 109^@`
(b) `hat(ACB) = 49^@` (may be seen in part (a))
attempt to substitute into the sine rule (or equivalent)
`(AC) / (sin 109^@) = 100 / (sin 49^@)`
`AC = 125` (km) `(=125.282...)`
Question 5
Ruhi buys a scoop of ice cream in the shape of a sphere with a radius of 3.4 cm. The ice cream is served in a cone, and it may be assumed that `1/5` of the volume of the ice cream is inside the cone. This is shown in the following diagram.

(a) Calculate the volume of ice cream that is not inside the cone.
The cone has a slant height of 11 cm and a radius of 3 cm.
The outside of the cone is covered with chocolate.
(b) Calculate the surface area of the cone that is covered with chocolate. Give your answer correct to the nearest cm2.
(a) `4/3 pi (3.4)^3`
multiplying their volume by `4/5`
`132 \ cm^3 (131.708... \ cm^3)`
(b) `pi times 3 times 11`
`103.672... \ cm^2` OR `33 pi \ cm^2`
`104 \ cm^2`
Question 6
The following diagram shows triangle ABC, with `AB=10, BC=x` and `AC=2x`.

Given that `cos hat C = 3/4`, find the area of the triangle.
Give your answer in the form `(p sqrt q)/2`, where `p,q in ZZ^+`.
attempt to use the cosine rule to find the value of `x`
`100 = x^2 + 4x^2 - 2(x)(2x)(3/4)`
`2x^2 = 100`
`x^2 = 50` OR `x = sqrt(50) \ (= 5sqrt(2))`
attempt to find `sin hat C` (seen anywhere)
`sin^2 hat(C) + (3/4)^2 = 1` OR `x^2+3^2=4^2` or right triangle with side 3 and hypotenuse 4
`sin hat C = sqrt 7 / 4`
correct substitution into the area formula using their value of `x` (or `x^2`) and their value of `sin hat C`
`A = 1/2 xx 5sqrt(2) xx 10sqrt(2) xx sqrt(7) / 4` or `A = 1/2 xx sqrt(50) xx 2sqrt(50) xx sqrt(7) / 4`
`A = (25sqrt(7)) / 2`
Question 7
In the following triangle ABC, `AB = sqrt 6` cm, `AC=10` cm and `cos hat (BAC)=1/5`.

Find the area of triangle ABC.
attempt to use Pythagoras’ theorem in a right-angled triangle.
`(sqrt (5^2-1^2) =) \ sqrt 24`
`sin hat (BAC) = sqrt 24 / 5` (may be seen in area formula)
attempt to use ‘Area `=1/2 ab sin C`' (must include their calculated value of `sin hat (BAC)`)
`=1/2 times 10 times sqrt 6 times sqrt 24 /5 = 12 \ (cm^2)`
Question 8
The following diagram shows a triangle ABC.

`AC = 15` cm, `BC = 10` cm, and `hat (ABC) = theta`.
Let `sin hat(CAB)=sqrt 3 / 3`.
(a) Given that `hat (ABC)` is acute, find `sin theta`.
(b) Find `cos (2 times hat (CAB))`.
(a) valid approach to find perpendicular length (may be seen on diagram)
e.g. 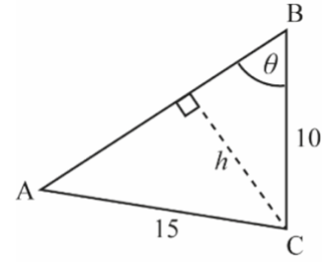
e.g. `h/15 = sqrt 3 / 3`
correct perpendicular length
e.g. `(15sqrt3)/3, 5sqrt3`
`sin theta = sqrt 3 /2`
(b) attempt to substitute into double-angle formula for cosine
`1-2(sqrt 3 /3)^2, 2 (sqrt 6 / 3)^2 -1, (sqrt 6 / 3)^2 - (sqrt 3 /3 )^2,`
`cos (2 theta)= 1 - 2(sqrt 3 / 2)^2, 1- 2sin^2(sqrt 3 /3)`
correct working
e.g. `1-2 times 3/9, 2 times 6/9 -1, 6/9 - 3/9`
`cos (2 times hat (CAB))=3/9=1/3`
Question 9
The following diagram shows a right triangle ABC. Point D lies on AB such that CD bisects `hat (ACB)`.

(a) Given that `sin theta = 3/5`, find the value of `cos theta`.
(b) Find the value of `cos 2 theta`.
(c) Hence or otherwise, find BC.
(a) valid approach
e.g. labelled sides on separate triangle, `sin^2 x + cos^2 x =1`
correct working
e.g. missing side is 4, `sqrt (1-(3/5)^2)`
`cos theta = 4/5`
(b) correct substitution into `cos 2 theta`
e.g. `2(16/25)-1, 1-2(3/5)^2, 16/25 - 9/25`
`cos 2 theta = 7/25`
(c) correct working
e.g. `7/25=14/(BC), \ BC=(14 times 25)/7`
`BC = 50` (cm)
Question 10
The following diagram shows triangle ABC, with `AB=3` cm, `BC=8` cm, and `hat(ABC)=pi/3`.

(a) Show that `AC=7` cm.
(b) The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.
(a) evidence of choosing the cosine rule
e.g. `c^2=a^2+b^2-2ab cos C`
correct substitution into RHS of cosine rule
e.g. `3^2+8^2-2 times 3 times 8 times cos (pi/3)`
evidence of correct value for `cos (pi/3)` (may be seen anywhere, including in cosine rule)
e.g. `cos(pi/3) = 1/2, AC^2 = 9 + 64 - (48 xx 1/2), 9 + 64 - 24`
correct working clearly leading to answer
e.g. `AC^2 = 49, b = sqrt(49)`
`AC = 7` (cm)
(b) correct substitution for semicircle
e.g. semicircle `= 1/2 (2pi xx 3.5), 1/2 xx pi xx 7, 3.5pi`
valid approach (seen anywhere)
e.g.perimeter`=`AB`+`BC`+`semicircle, `3 + 8 + (1/2 xx 2 xx pi xx 7/2), 8 + 3 + 3.5pi`
`11 + 7/2 pi = 3.5pi + 11 \ (cm)`
Question 1
Consider a triangle ABC, where AC = 12, CB = 7, and `hat (BAC) = 25^@`.
Find the smallest possible perimeter of triangle ABC.
Question 2
A farmer is placing posts at points A, B, and C in the ground to mark the boundaries of a triangular piece of land on his property.
From point A, he walks due west 230 metres to point B.
From point B, he walks 175 metres on a bearing of `063^@` to reach point C.
This is shown in the following diagram.

(a) Find the distance from point A to point C.
(b) Find the area of this piece of land.
(c) Find `hat (CAB)`.
The farmer wants to divide the piece of land into two sections. He will put a post at point D, which is between A and C. He wants the boundary BD to divide the piece of land such that the sections have equal area. This is shown in the following diagram.

(d) Find the distance from point B to point D.
Question 3
The following diagram shows triangle ABC, with `AC=24`, `BC=17`, and `hat(ABC)=113^@`.

(a) Find `hat (BAC)`.
(b) Find AB.
Question 4
Jason sails his boat from point A for a distance of 100 km, on a bearing of `112^@`, to arrive at point B. He then sails on a bearing of `041^@` to point C. Jason’s journey is shown in the diagram.

(a) Find `hat(ABC)`.
Point C is directly east of point A.
(b) Calculate the distance that Jason sails to return directly from point C to point A.
Question 5
Ruhi buys a scoop of ice cream in the shape of a sphere with a radius of 3.4 cm. The ice cream is served in a cone, and it may be assumed that `1/5` of the volume of the ice cream is inside the cone. This is shown in the following diagram.

(a) Calculate the volume of ice cream that is not inside the cone.
The cone has a slant height of 11 cm and a radius of 3 cm.
The outside of the cone is covered with chocolate.
(b) Calculate the surface area of the cone that is covered with chocolate. Give your answer correct to the nearest cm2.
Question 6
The following diagram shows triangle ABC, with `AB=10, BC=x` and `AC=2x`.

Given that `cos hat C = 3/4`, find the area of the triangle.
Give your answer in the form `(p sqrt q)/2`, where `p,q in ZZ^+`.
Question 7
In the following triangle ABC, `AB = sqrt 6` cm, `AC=10` cm and `cos hat (BAC)=1/5`.

Find the area of triangle ABC.
Question 8
The following diagram shows a triangle ABC.

`AC = 15` cm, `BC = 10` cm, and `hat (ABC) = theta`.
Let `sin hat(CAB)=sqrt 3 / 3`.
(a) Given that `hat (ABC)` is acute, find `sin theta`.
(b) Find `cos (2 times hat (CAB))`.
Question 9
The following diagram shows a right triangle ABC. Point D lies on AB such that CD bisects `hat (ACB)`.

(a) Given that `sin theta = 3/5`, find the value of `cos theta`.
(b) Find the value of `cos 2 theta`.
(c) Hence or otherwise, find BC.
Question 10
The following diagram shows triangle ABC, with `AB=3` cm, `BC=8` cm, and `hat(ABC)=pi/3`.

(a) Show that `AC=7` cm.
(b) The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.

Find the exact perimeter of this shape.