Question 1
The graph of a function g is given in the diagram below.
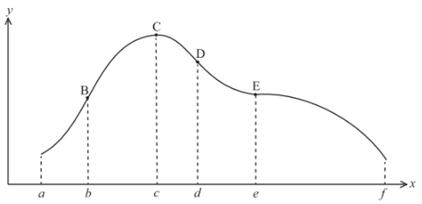
The gradient of the curve has its maximum value at point B and its minimum value at point D. The tangent is horizontal at points C and E.
(a) Complete the table below, by stating whether the first derivative is positive or negative, and whether the second derivative is positive or negative.
| Interval | `g'` | `g^('')` |
| `a < x < b` |
|
|
| `e < x < f` |
|
|
(b) Complete the table below by noting the points on the graph described by the following conditions.
| Conditions | Point |
| `g'(x)=0, g^('') (x) <0` |
|
| `g'(x)<0, g^('')(x)<0` |
|
Mark as Complete
Mark Scheme
Question 2
The following diagram shows part of the curve of a function f. The points A, B, C, D and E lie on the curve, where B is a minimum point and D is a maximum point.

(a) Complete the following table, noting whether `f'(x)` is positive, negative or zero at the given points.
| A | B | E | |
| `f'(x)` |
|
|
|
(b) Complete the following table, noting whether `f^('')(x)` is positive, negative or zero at the given points.
| A | B | E | |
| `f^('')(x)` |
|
|
|
Mark as Complete
Mark Scheme
Question 3
The diagram shows the graph of `y=f(x)`

On the grid below sketch the graph of `y=f'(x)`
Mark as Complete
Mark Scheme
Question 4
Figure 1 shows the graphs of the functions f1 , f2 , f3 , f4 .
Figure 2 includes the graphs of the derivatives of the functions shown in Figure 1, e.g. the derivative of f1 is shown in diagram (d).

Complete the table below by matching each function with its derivative.
| Function | Derivative diagram |
| f1 | (d) |
| f2 |
|
| f3 |
|
| f4 |
|
Mark as Complete
Mark Scheme
Question 5
Part of the graph of the periodic function f is shown below. The domain of f is `0<=x<=15` and the period is 3.
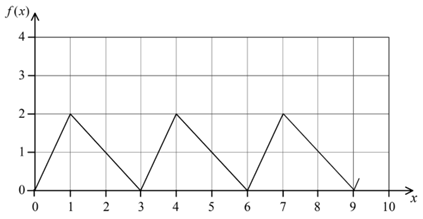
(a) Find
(i) `f(2)`
(ii) `f'(6.5)`
(iii) `f'(14)`
(b) How many solutions are there to the equation `f(x)=1` over the given domain?
Mark as Complete
Mark Scheme
Question 6
(a) Let `f(x)=e^(5x)`. Write down `f^' (x)`.
(b) Let `g(x)=sin2x`. Write down `g^' (x)`.
(c) Let `h(x)=e^(5x)sin2x`. Find `h^' (x)`.
Mark as Complete
Mark Scheme
Question 7
The following diagram shows the graph of f’ , the derivative of f .
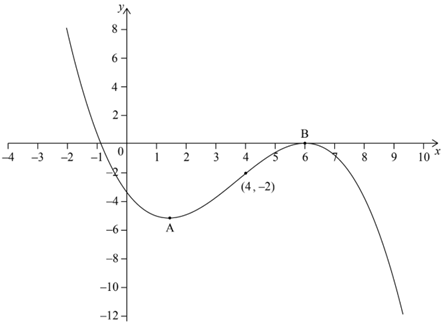
The graph of f ' has a local minimum at A, a local maximum at B and passes through (4, -2).
(a) The point P(4, 3) lies on the graph of the function, f .
(i) Write down the gradient of the curve of f at P .
(ii) Find the equation of the normal to the curve of f at P .
(b) Determine the concavity of the graph of f when `4 < x < 5` and justify your answer.
Mark as Complete
Mark Scheme
Question 8
A function `f(x)` has derivative `f^' (x)=3x^2+18x`. The graph of `f` has an `x`-intercept at `x = -1`.
(a) Find `f(x)`.
(b) The graph of `f` has a point of inflexion at `x = p`. Find `p`.
(c) Find the values of `x` for which the graph of `f` is concave-down.
Mark as Complete
Mark Scheme
Question 9
Let `y=f(x)`, for `-0.5≤x≤6.5.`. The following diagram shows the graph of `f'`, the derivative of `f`.

The graph of `f'` has a local maximum when `x=2`, a local minimum when `x=4`, and it crosses the `x`-axis at the point `(5,0)`.
(a) Explain why the graph of `f` has a local minimum when `x=5`.
(b) Find the set of values of `x` for which the graph of f is concave down.
Mark as Complete
Mark Scheme
Question 10
Let `f(x)=e^(-2x)`.
(a) Write down `f'(x)`, `f^('')(x)` and `f^((3))(x)`.
(b) Find an expression for `f^((n))(x)`.
Mark as Complete
Mark Scheme
Question 1
The graph of a function g is given in the diagram below.

The gradient of the curve has its maximum value at point B and its minimum value at point D. The tangent is horizontal at points C and E.
(a) Complete the table below, by stating whether the first derivative is positive or negative, and whether the second derivative is positive or negative.
| Interval | `g'` | `g^('')` |
| `a < x < b` |
|
|
| `e < x < f` |
|
|
(b) Complete the table below by noting the points on the graph described by the following conditions.
| Conditions | Point |
| `g'(x)=0, g^('') (x) <0` |
|
| `g'(x)<0, g^('')(x)<0` |
|
(a)
| Interval | `g'` | `g^('')` |
| `a < x < b` | positive | positive |
| `e < x < f` | negative | negative |
(b)
| Conditions | Point |
| `g'(x)=0, g^('') (x) <0` | C |
| `g'(x)<0, g^('')(x)<0` | D |
Question 2
The following diagram shows part of the curve of a function f. The points A, B, C, D and E lie on the curve, where B is a minimum point and D is a maximum point.

(a) Complete the following table, noting whether `f'(x)` is positive, negative or zero at the given points.
| A | B | E | |
| `f'(x)` |
|
|
|
(b) Complete the following table, noting whether `f^('')(x)` is positive, negative or zero at the given points.
| A | B | E | |
| `f^('')(x)` |
|
|
|
(a)
|
| A | B | E |
| `f'(x)` | negative | 0 | negative |
(b)
|
| A | C | E |
| `f^('')(x)` | positive | positive | negative |
Question 3
The diagram shows the graph of `y=f(x)`

On the grid below sketch the graph of `y=f'(x)`


Question 4
Figure 1 shows the graphs of the functions f1 , f2 , f3 , f4 .
Figure 2 includes the graphs of the derivatives of the functions shown in Figure 1, e.g. the derivative of f1 is shown in diagram (d).

Complete the table below by matching each function with its derivative.
| Function | Derivative diagram |
| f1 | (d) |
| f2 |
|
| f3 |
|
| f4 |
|
| Function | Derivative diagram |
| f1 | (d) |
| f2 | (e) |
| f3 | (b) |
| f4 | (a) |
Question 5
Part of the graph of the periodic function f is shown below. The domain of f is `0<=x<=15` and the period is 3.

(a) Find
(i) `f(2)`
(ii) `f'(6.5)`
(iii) `f'(14)`
(b) How many solutions are there to the equation `f(x)=1` over the given domain?
(a) (i) 1
(ii) 2
(iii) f’(14) = f’(2) (or f’(5) or f’(80)
= -1
(b) There are five repeated periods of the graph, each with two solutions,
(i.e. number of solutions is 5 x 2)
= 10
Question 6
(a) Let `f(x)=e^(5x)`. Write down `f^' (x)`.
(b) Let `g(x)=sin2x`. Write down `g^' (x)`.
(c) Let `h(x)=e^(5x)sin2x`. Find `h^' (x)`.
(a) `f^' (x)=5e^5x`
(b) `g^' (x)=2cos2x`
(c) `h^'=fg^'+gf^'`
`=e^(5x) (2cos2x)+sin2x(5e^(5x) )`
Question 7
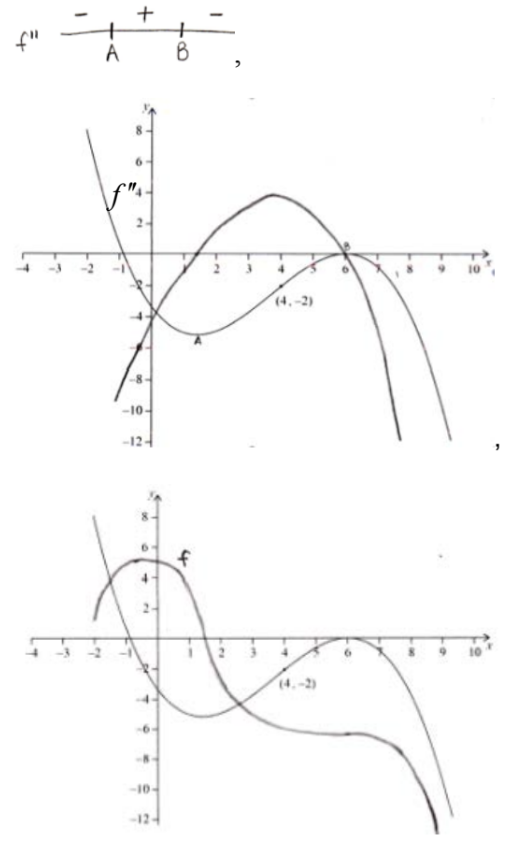
The following diagram shows the graph of f’ , the derivative of f .

The graph of f ' has a local minimum at A, a local maximum at B and passes through (4, -2).
(a) The point P(4, 3) lies on the graph of the function, f .
(i) Write down the gradient of the curve of f at P .
(ii) Find the equation of the normal to the curve of f at P .
(b) Determine the concavity of the graph of f when `4 < x < 5` and justify your answer.
(a) (i) -2
(ii) gradient of normal `=1/2`
attempt to substitute their normal gradient and coordinates of P (in any order)
eg `y-4=1/2(x-3),3=1/2(4)+b,b=1`
`y-3=1/2(x-4),y=1/2 x+1,x-2y+2=0`
(b) correct answer and valid reasoning
answer: eg graph of f is concave up, concavity is positive (between `4 < x < 5` )
reason: eg slope of `f'` is positive, `f'` is increasing, `f^('') > 0`, sign chart (must clearly be for `f^('')` and show A and B)
Question 8
A function `f(x)` has derivative `f^' (x)=3x^2+18x`. The graph of `f` has an `x`-intercept at `x = -1`.
(a) Find `f(x)`.
(b) The graph of `f` has a point of inflexion at `x = p`. Find `p`.
(c) Find the values of `x` for which the graph of `f` is concave-down.
(a) evidence of integration
eg `intf'(x)`
correct integration (accept absence of C )
eg `x^3+18/2 x^2+C,x^3+9x^2`
attempt to substitute `x=-1` into their `f=0` (must have C )
eg `(-1)^3+9(-1)^2+C=0,-1+9+C=0`
correct working
eg `8+C=0,C=-8`
`f(x)=x^3+9x^2-8`
(b) recognizing that `f^('')=0` (seen anywhere)
correct expression for `f^('')`
eg `6x+18,6p+18`
correct working
`6p+18=0`
`p=-3`
(c) valid attempt to use `f^('')(x)` to determine concavity
eg `f^('')(x)<0,f^('')(-2),f^('')(-4),6x+18≤0` ![]()
correct working
eg `6x+18<0,f^('')(-2)=6,f^('')(-4)=-6` ![]()
f concave down for `x < -3` (do not accept `x <= -3` )
Question 9
Let `y=f(x)`, for `-0.5≤x≤6.5.`. The following diagram shows the graph of `f'`, the derivative of `f`.

The graph of `f'` has a local maximum when `x=2`, a local minimum when `x=4`, and it crosses the `x`-axis at the point `(5,0)`.
(a) Explain why the graph of `f` has a local minimum when `x=5`.
(b) Find the set of values of `x` for which the graph of f is concave down.
(a)
| Interval | `g'` | `g^('')` |
| `a < x < b` | positive | positive |
| `e < x < f` | negative | negative |
(b)
| Conditions | Point |
| `g'(x)=0, g^('') (x) <0` | C |
| `g'(x)<0, g^('')(x)<0` | D |
Question 10
Let `f(x)=e^(-2x)`.
(a) Write down `f'(x)`, `f^('')(x)` and `f^((3))(x)`.
(b) Find an expression for `f^((n))(x)`.
(a) `f^' (x)=-2e^(-2x),f^('')(x)=4e^(-2x),f^((3)) (x)=-8e^(-2x)`
(b) `f^((n)) (x)=(-2)^n e^(-2x)` (accept `(-1)^n 2^n e^(-2x),(-2)^n f(x)` )
Question 1
The graph of a function g is given in the diagram below.

The gradient of the curve has its maximum value at point B and its minimum value at point D. The tangent is horizontal at points C and E.
(a) Complete the table below, by stating whether the first derivative is positive or negative, and whether the second derivative is positive or negative.
| Interval | `g'` | `g^('')` |
| `a < x < b` |
|
|
| `e < x < f` |
|
|
(b) Complete the table below by noting the points on the graph described by the following conditions.
| Conditions | Point |
| `g'(x)=0, g^('') (x) <0` |
|
| `g'(x)<0, g^('')(x)<0` |
|
Question 2
The following diagram shows part of the curve of a function f. The points A, B, C, D and E lie on the curve, where B is a minimum point and D is a maximum point.

(a) Complete the following table, noting whether `f'(x)` is positive, negative or zero at the given points.
| A | B | E | |
| `f'(x)` |
|
|
|
(b) Complete the following table, noting whether `f^('')(x)` is positive, negative or zero at the given points.
| A | B | E | |
| `f^('')(x)` |
|
|
|
Question 3
The diagram shows the graph of `y=f(x)`

On the grid below sketch the graph of `y=f'(x)`

Question 4
Figure 1 shows the graphs of the functions f1 , f2 , f3 , f4 .
Figure 2 includes the graphs of the derivatives of the functions shown in Figure 1, e.g. the derivative of f1 is shown in diagram (d).

Complete the table below by matching each function with its derivative.
| Function | Derivative diagram |
| f1 | (d) |
| f2 |
|
| f3 |
|
| f4 |
|
Question 5
Part of the graph of the periodic function f is shown below. The domain of f is `0<=x<=15` and the period is 3.

(a) Find
(i) `f(2)`
(ii) `f'(6.5)`
(iii) `f'(14)`
(b) How many solutions are there to the equation `f(x)=1` over the given domain?
Question 6
(a) Let `f(x)=e^(5x)`. Write down `f^' (x)`.
(b) Let `g(x)=sin2x`. Write down `g^' (x)`.
(c) Let `h(x)=e^(5x)sin2x`. Find `h^' (x)`.
Question 7
The following diagram shows the graph of f’ , the derivative of f .

The graph of f ' has a local minimum at A, a local maximum at B and passes through (4, -2).
(a) The point P(4, 3) lies on the graph of the function, f .
(i) Write down the gradient of the curve of f at P .
(ii) Find the equation of the normal to the curve of f at P .
(b) Determine the concavity of the graph of f when `4 < x < 5` and justify your answer.
Question 8
A function `f(x)` has derivative `f^' (x)=3x^2+18x`. The graph of `f` has an `x`-intercept at `x = -1`.
(a) Find `f(x)`.
(b) The graph of `f` has a point of inflexion at `x = p`. Find `p`.
(c) Find the values of `x` for which the graph of `f` is concave-down.
Question 9
Let `y=f(x)`, for `-0.5≤x≤6.5.`. The following diagram shows the graph of `f'`, the derivative of `f`.

The graph of `f'` has a local maximum when `x=2`, a local minimum when `x=4`, and it crosses the `x`-axis at the point `(5,0)`.
(a) Explain why the graph of `f` has a local minimum when `x=5`.
(b) Find the set of values of `x` for which the graph of f is concave down.
Question 10
Let `f(x)=e^(-2x)`.
(a) Write down `f'(x)`, `f^('')(x)` and `f^((3))(x)`.
(b) Find an expression for `f^((n))(x)`.