Question 1
The function `f` is defined by `f(x) = 8x`. For what value of `x` does `f(x) = 72`?
A) `8`
B) `9`
C) `64`
D) `80`
Mark as Complete
Mark Scheme
Question 2
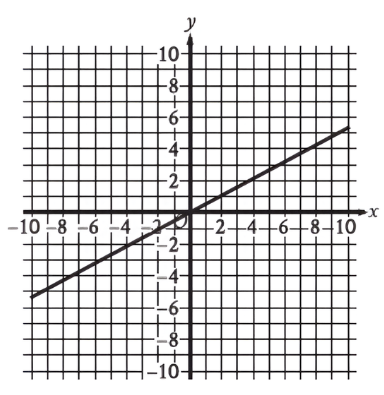
The graph of function `f` is shown, where `y = f(x)`. Which of the following describes function `f`?
A) Increasing linear
B) Decreasing linear
C) Increasing exponential
D) Decreasing exponential
Mark as Complete
Mark Scheme
Question 3
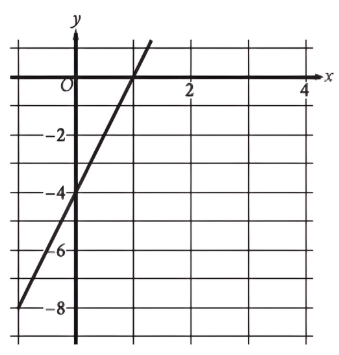
The graph of the function `f` is shown, where `y = f(x)`. What is the `y`-intercept of the graph?
A) `(0, -1)`
B) `(0, -4)`
C) `(0, 1)`
D) `(0, 4)`
Mark as Complete
Mark Scheme
Question 4
`f (x) = 14 + 4x`
The function `f` represents the total cost, in dollars, of attending an arcade when `x` games are played. How many games can be played for a total cost of `$58`?
Mark as Complete
Mark Scheme
Question 5
`f(x) = x + b`
For the linear function `f`, `b` is a constant. When `x = 0`, `f(x) = 30`. What is the value of `b`?
A) `-30`
B) `-1/30`
C) `1/30`
D) `30`
Mark as Complete
Mark Scheme
Question 6
An airplane descends from an altitude of `9500` feet to `5000` feet at a constant rate of `400` feet per minute. What type of function best models the relationship between the descending airplane’s altitude and time?
A) Decreasing exponential
B) Decreasing linear
C) Increasing exponential
D) Increasing linear
Mark as Complete
Mark Scheme
Question 7
The function `f` defined by `f(t) = 14t + 9` gives the estimated length, in inches, of a vine plant `t` months after Tavon purchased it. Which of the following is the best interpretation of `9` in this context?
A) Tavon will keep the vine plant for `9` months.
B) The vine plant is expected to grow `9` inches each month.
C) The vine plant is expected to grow to a maximum length of `9` inches.
D) The estimated length of the vine plant was `9` inches when Tavon purchased it.
Mark as Complete
Mark Scheme
Question 8
The total cost `f(x)`, in dollars, to lease a car for `36` months from a particular car dealership is given by `f(x) = 36x + "1,000"`, where `x` is the monthly payment, in dollars. What is the total cost to lease a car when the monthly payment is `$400`?
A) `$"13,400"`
B) `$"13,000"`
C) `$"15,400"`
D) `$"37,400"`
Mark as Complete
Mark Scheme
Question 9
The function g is defined by `g(x) = 10x + 8`. What is the value of `g(x)` when `x = 8`?
A) `0`
B) `8`
C) `10`
D) `88`
Mark as Complete
Mark Scheme
Question 10
The relationship between two variables, `x` and `y`, is linear. For every increase in the value of `x` by `1`, the value of `y` increases by `8`. When the value of `x` is `2`, the value of `y` is `18`. Which equation represents this relationship?
A) `y = 2x + 18`
B) `y = 2x + 8`
C) `y = 8x + 2`
D) `y = 3x + 26`
Mark as Complete
Mark Scheme
Question 11
In the linear function `f`, `f(0) = 8` and `f(1) = 12`. Which equation defines `f`?
A) `f(x) = 12x + 8`
B) `f(x) = 4x`
C) `f(x) = 4x + 12`
D) `f(x) = 4x + 8`
Mark as Complete
Mark Scheme
Question 1
The function `f` is defined by `f(x) = 8x`. For what value of `x` does `f(x) = 72`?
A) `8`
B) `9`
C) `64`
D) `80`
Answer: B
To find the value of `x`, setting `f(x)` to `72` to get `72 = 8x`. Then, divide both sides by `8`, which results in `x = 9`.
Question 2

The graph of function `f` is shown, where `y = f(x)`. Which of the following describes function `f`?
A) Increasing linear
B) Decreasing linear
C) Increasing exponential
D) Decreasing exponential
The `y`-intercept is the point where the graph crosses the `y`-axis. Looking at the graph, the line intersects the `y`-axis at the point `(0, -4)`.
Question 3

The graph of the function `f` is shown, where `y = f(x)`. What is the `y`-intercept of the graph?
A) `(0, -1)`
B) `(0, -4)`
C) `(0, 1)`
D) `(0, 4)`
Answer: B
The `y`-intercept is the point where the graph crosses the `y`-axis. Looking at the graph, the line intersects the `y`-axis at the point `(0, -4)`.
Question 4
`f (x) = 14 + 4x`
The function `f` represents the total cost, in dollars, of attending an arcade when `x` games are played. How many games can be played for a total cost of `$58`?
Answer: `11`
Set the total cost, `f(x)`, to `58`to yield the linear equation: `58 = 14 + 4x`. To solve for `x`, subtract `14` from both sides to get `44 = 4x`. Then, divide by `4`, which results in `x = 11`. So, `11` games can be played for `$58`.
Question 5
`f(x) = x + b`
For the linear function `f`, `b` is a constant. When `x = 0`, `f(x) = 30`. What is the value of `b`?
A) `-30`
B) `-1/30`
C) `1/30`
D) `30`
Answer: D
Substitute the given value into the function. When `x = 0`, `f(x) = 30`, so the equation becomes `30 = 0 + b`. This simplifies to `b = 30`. The constant `b` represents the `y`-intercept of the function.
Question 6
An airplane descends from an altitude of `9500` feet to `5000` feet at a constant rate of `400` feet per minute. What type of function best models the relationship between the descending airplane’s altitude and time?
A) Decreasing exponential
B) Decreasing linear
C) Increasing exponential
D) Increasing linear
Answer: B
Recall that a quantity changes linearly with time if the difference between sucessive time periods is constant. On the other hand, a quantity changes exponentially if the ratio in the quantity between successive time periods is constant. In this question, it is given that the airplane descends at a constant rate of `400` feet per minute. Since the altitude decreases by a constant amount during each fixed time period, the relationship between the airplane’s altitude and time is linear. Since the airplane descends from an altitude of `9500` feet to `5000` feet, the airplane’s altitude is decreasing with time. Thus, the relationship is best modeled by a decreasing linear function.
Question 7
The function `f` defined by `f(t) = 14t + 9` gives the estimated length, in inches, of a vine plant `t` months after Tavon purchased it. Which of the following is the best interpretation of `9` in this context?
A) Tavon will keep the vine plant for `9` months.
B) The vine plant is expected to grow `9` inches each month.
C) The vine plant is expected to grow to a maximum length of `9` inches.
D) The estimated length of the vine plant was `9` inches when Tavon purchased it.
Answer: D
In a linear function of the form `y = mx + b`, the value of `b` is the initial value, or the value when the input is `0`. In this function, `t = 0` represents the time Tavon purchased the plant. Therefore, `9` represents the estimated length of the plant in inches at the time of purchase.
Question 8
The total cost `f(x)`, in dollars, to lease a car for `36` months from a particular car dealership is given by `f(x) = 36x + "1,000"`, where `x` is the monthly payment, in dollars. What is the total cost to lease a car when the monthly payment is `$400`?
A) `$"13,400"`
B) `$"13,000"`
C) `$"15,400"`
D) `$"37,400"`
Answer: C
It is given that `f(x)` is the total cost, in dollars, to lease a car from this dealership with a monthly payment of `x` dollars. Therefore, the total cost, in dollars, to lease the car when the monthly payment is `$400` is represented by the value of `f(x)` when `x = 400`. Substituting `400` for `x` in the equation `f(x) = 36x + "1,000"` yields `f(400) = 36(400) + "1,000"`, or `f(400) = "15,400"`. Thus, when the monthly payment is `$400`, the total cost to lease a car is `$"15,400"`.
Question 9
The function g is defined by `g(x) = 10x + 8`. What is the value of `g(x)` when `x = 8`?
A) `0`
B) `8`
C) `10`
D) `88`
Answer: D
The value of `g(x)` when `x = 8` can be found by substituting `8` for `x` in the equation `g(x) = 10x + 8`. This yields `g(8) = 10(8) + 8`, or `g(8) = 88`. Therefore, when `x = 8`, the value of `g(x)` is `88`.
Question 10
The relationship between two variables, `x` and `y`, is linear. For every increase in the value of `x` by `1`, the value of `y` increases by `8`. When the value of `x` is `2`, the value of `y` is `18`. Which equation represents this relationship?
A) `y = 2x + 18`
B) `y = 2x + 8`
C) `y = 8x + 2`
D) `y = 3x + 26`
Answer: C
The statement that "for every increase in the value of `x` by 1, the value of `y` increases by `8`" means the slope (`m`) of the line is `8/1`, or `8`. The equation is `y = 8x + b`.
To find `b`, use the point (2, 18): `18 = 8(2) + b`, which simplifies to `18 = 16 + b`. Solving for `b` gives `b=2`. Therefore, the equation is `y = 8x + 2`.
Question 11
In the linear function `f`, `f(0) = 8` and `f(1) = 12`. Which equation defines `f`?
A) `f(x) = 12x + 8`
B) `f(x) = 4x`
C) `f(x) = 4x + 12`
D) `f(x) = 4x + 8`
Answer: D
Since `f` is a linear function, it can be defined by an equation of the form `f(x) = ax + b`, where `a` and `b` are constants. It is given that `f(0) = 8`. Substituting `0` for `x` and `8` for `f(x)` in the equation `f(x) = ax + b` yields `8 = a(0) + b`, or `8 = b`. Substituting `8` for `b` in the equation `f(x) = ax + b` yields `f(x) = ax + 8`. Similarly, since `f(1) = 12`, substituting `1` for `x` and `12` for `f(x)` in the equation `f(x) = ax + 8` yields `12 = a(1) + 8`, or `12 = a + 8`. Subtracting `8` from both sides of this equation yields `a = 4`. Substituting `4` for `a` in the equation `f(x) = ax + 8` yields `f(x) = 4x + 8`. Therefore, an equation that defines `f` is `f(x) = 4x + 8`.
Question 1
The function `f` is defined by `f(x) = 8x`. For what value of `x` does `f(x) = 72`?
A) `8`
B) `9`
C) `64`
D) `80`
Question 2

The graph of function `f` is shown, where `y = f(x)`. Which of the following describes function `f`?
A) Increasing linear
B) Decreasing linear
C) Increasing exponential
D) Decreasing exponential
Question 3

The graph of the function `f` is shown, where `y = f(x)`. What is the `y`-intercept of the graph?
A) `(0, -1)`
B) `(0, -4)`
C) `(0, 1)`
D) `(0, 4)`
Question 4
`f (x) = 14 + 4x`
The function `f` represents the total cost, in dollars, of attending an arcade when `x` games are played. How many games can be played for a total cost of `$58`?
Question 5
`f(x) = x + b`
For the linear function `f`, `b` is a constant. When `x = 0`, `f(x) = 30`. What is the value of `b`?
A) `-30`
B) `-1/30`
C) `1/30`
D) `30`
Question 6
An airplane descends from an altitude of `9500` feet to `5000` feet at a constant rate of `400` feet per minute. What type of function best models the relationship between the descending airplane’s altitude and time?
A) Decreasing exponential
B) Decreasing linear
C) Increasing exponential
D) Increasing linear
Question 7
The function `f` defined by `f(t) = 14t + 9` gives the estimated length, in inches, of a vine plant `t` months after Tavon purchased it. Which of the following is the best interpretation of `9` in this context?
A) Tavon will keep the vine plant for `9` months.
B) The vine plant is expected to grow `9` inches each month.
C) The vine plant is expected to grow to a maximum length of `9` inches.
D) The estimated length of the vine plant was `9` inches when Tavon purchased it.
Question 8
The total cost `f(x)`, in dollars, to lease a car for `36` months from a particular car dealership is given by `f(x) = 36x + "1,000"`, where `x` is the monthly payment, in dollars. What is the total cost to lease a car when the monthly payment is `$400`?
A) `$"13,400"`
B) `$"13,000"`
C) `$"15,400"`
D) `$"37,400"`
Question 9
The function g is defined by `g(x) = 10x + 8`. What is the value of `g(x)` when `x = 8`?
A) `0`
B) `8`
C) `10`
D) `88`
Question 10
The relationship between two variables, `x` and `y`, is linear. For every increase in the value of `x` by `1`, the value of `y` increases by `8`. When the value of `x` is `2`, the value of `y` is `18`. Which equation represents this relationship?
A) `y = 2x + 18`
B) `y = 2x + 8`
C) `y = 8x + 2`
D) `y = 3x + 26`
Question 11
In the linear function `f`, `f(0) = 8` and `f(1) = 12`. Which equation defines `f`?
A) `f(x) = 12x + 8`
B) `f(x) = 4x`
C) `f(x) = 4x + 12`
D) `f(x) = 4x + 8`