Question 1
`k² - 53 = 91`
What is the positive solution to the given equation?
A) `144`
B) `72`
C) `38`
D) `12`
Mark as Complete
Mark Scheme
Question 2
`(55) / (x + 6) = x`
What is the positive solution to the given equation?
Mark as Complete
Mark Scheme
Question 3
A manager is responsible for ordering supplies for a shaved ice shop. The shop's inventory starts with `"4,500"` paper cups, and the manager estimates that `70` of these paper cups are used each day. Based on this estimate, in how many days will the supply of paper cups reach `"1,700"`?
A) `20`
B) `40`
C) `60`
D) `80`
Mark as Complete
Mark Scheme
Question 4
`g(x) = 11 times (1/12)^x`
If the given function `g` is graphed in the `xy`-plane, where`y = g(x)`, what is the `y`-intercept of the graph?
A) `(0, 11)`
B) `(0, 132)`
C) `(0, 1)`
D) `(0, 12)`
Mark as Complete
Mark Scheme
Question 5
`(x + 2)(x − 5)(x + 9) = 0`
What is a positive solution to the given equation?
A) `3`
B) `4`
C) `5`
D) `18`
Mark as Complete
Mark Scheme
Question 6
A rectangle has a length of `x` units and a width of `x−15` units. If the rectangle has an area of `76` square units, what is the value of `x`?
A) `4`
B) `19`
C) `23`
D) `76`
Mark as Complete
Mark Scheme
Question 7
A rectangle has an area of `155` square inches. The length of the rectangle is `4` inches less than `7` times the width of the rectangle. What is the width of the rectangle, in inches?
Mark as Complete
Mark Scheme
Question 8
The number of bacteria in a liquid medium doubles every day. There are `"44,000"` bacteria in the liquid medium at the start of an observation. Which represents the number of bacteria, `y`, in the liquid medium `t` days after the start of the observation?
A) `y= 1/2("44,000")^t`
B) y= `2("44,000")^t`
C) `y = "44,000"(1/2)^t`
D) `y = "44,000"(2)^t`
Mark as Complete
Mark Scheme
Question 9
`x² = -841`
How many distinct real solutions does the given equation have?
A) Exactly one
B) Exactly two
C) Infinitely many
D) Zero
Mark as Complete
Mark Scheme
Question 10
If `4^(8c) = root(3)(4^7)`, what is the value of `c`?
Mark as Complete
Mark Scheme
Question 11
In the `xy`-plane, a line with equation `2y = c` for some constant `c` intersects a parabola at exactly one point. If the parabola has equation `y= -2x^2 + 9x`, what is the value of `c`?
Mark as Complete
Mark Scheme
Question 12
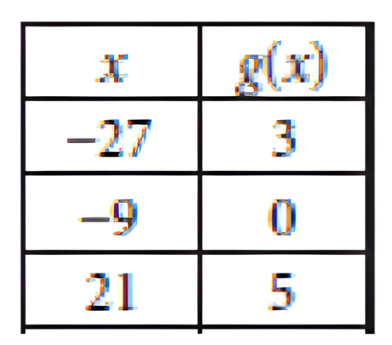
The table shows three values of `x` and their corresponding values of `g(x)`, where `g(x) = f(x) / (x + 3)` and `f` is a linear function. What is the `y`-intercept of the graph of `y = f(x)` in the `xy`-plane?
A) `(0, 36)`
B) `(0, 12)`
C) `(0, 4)`
D) `(0, -9)`
Mark as Complete
Mark Scheme
Question 1
`k² - 53 = 91`
What is the positive solution to the given equation?
A) `144`
B) `72`
C) `38`
D) `12`
To find the positive solution, first add `53` to both sides of the equation `k² - 53 = 91` to get `k² = 144`. Then, take the square root of both sides, which gives `k = ±12`. The positive solution is `12`.
Question 2
`(55) / (x + 6) = x`
What is the positive solution to the given equation?
Answer: `5`
The correct answer is `5`. Multiplying both sides of the given equation by `x + 6` results in `55 = x(x + 6)`. Applying the distributive property of multiplication to the right-hand side of this equation results in `55 = x^2 + 6x`. Subtracting `55` from both sides of this equation results in `0 = x^2 + 6x - 55`. The right-hand side of this equation can be rewritten by factoring. Since `11` and `-5` add to `6` and multiply to `-55`, we have `x^2 + 6x - 55 = (x + 11)(x-5)`. The equation `0 = x^2 + 6x - 55` can thus be rewritten as `0 = (x + 11)(x - 5)`. In order for `0 = (x + 11)(x - 5)` to be true, we must have either `x + 11 = 0`, or `x - 5 = 0`. In the former case, `x = -11`; while in the latter `x = 5`. This shows that positive solution to the given equation is `5`.
Question 3
A manager is responsible for ordering supplies for a shaved ice shop. The shop's inventory starts with `"4,500"` paper cups, and the manager estimates that `70` of these paper cups are used each day. Based on this estimate, in how many days will the supply of paper cups reach `"1,700"`?
A) `20`
B) `40`
C) `60`
D) `80`
Answer: B
Let `x` be the number of days. The number of cups remaining can be modeled by the equation `"4,500" - 70x`. To find when the supply will reach `"1,700"`, solve the equation `4,500 - 70x = "1,700"`. Subtracting `"4,500"` from both sides gives `-70x = -"2,800"`. Dividing both sides by `-70` gives `x = 40`. So, the supply will reach `"1,700"` in 40 days.
Question 4
`g(x) = 11 times (1/12)^x`
If the given function `g` is graphed in the `xy`-plane, where`y = g(x)`, what is the `y`-intercept of the graph?
A) `(0, 11)`
B) `(0, 132)`
C) `(0, 1)`
D) `(0, 12)`
Answer: A
The `y`-intercept of the graph of the given function is the point `(0, g(0))`. Substituting `0` for `x` in the given function yields `g(0) = 11 times (1/12)^0`. Since any nonzero number raised to the `0^{th}` power is `1`, this gives `g(0) = 11 times 1`, or `g(0) = 11`. The `y`-intercept of the graph is, therefore, the point `(0, 11)`.
Question 5
`(x + 2)(x − 5)(x + 9) = 0`
What is a positive solution to the given equation?
A) `3`
B) `4`
C) `5`
D) `18`
Answer: C
According to the zero product property, if a product of factors is zero, at least one of the factors must be zero. Setting each factor equal to zero gives:
`x + 2 = 0`→ `x = -2`
`x - 5 = 0` → `x = 5`
`x + 9 = 0` → `x = -9`
The only positive solution among these is `5`.
Question 6
A rectangle has a length of `x` units and a width of `x−15` units. If the rectangle has an area of `76` square units, what is the value of `x`?
A) `4`
B) `19`
C) `23`
D) `76`
Answer: A
The area of a rectangle is equal to its length multiplied by its width. Multiplying the given length, `x` units, by the given width, `(x – 15)` units, yields `x(x – 15)` square units. If the rectangle has an area of `76` square units, it follows that `x(x – 15) = 76`, or `x^2 – 15x = 76`. Subtracting `76` from both sides of this equation yields `x^2 – 15x – 76 = 0`. Factoring the left-hand side of this equation yields `(x – 19)(x + 4) = 0`. Applying the zero product property to this equation yields two solutions: `x = 19` and `x = –4`. Since `x` is the rectangle’s length, in units, which must be positive, the value of `x` is `19`.
Question 7
A rectangle has an area of `155` square inches. The length of the rectangle is `4` inches less than `7` times the width of the rectangle. What is the width of the rectangle, in inches?
Answer: `5`
Let `w` be the width. The length `l` can be expressed as `l = 7w - 4`.
The area of a rectangle is `A = l xx w`.
Substituting the given values, we get `155 = (7w - 4) * w`.
This simplifies to the quadratic equation `7w² - 4w - 155 = 0`.
Factoring this equation gives `(7w + 31)(w - 5) = 0`.
The solutions are `w = -31/7` and `w = 5`. Since width cannot be negative, the width of the rectangle is `5` inches.
Question 8
The number of bacteria in a liquid medium doubles every day. There are `"44,000"` bacteria in the liquid medium at the start of an observation. Which represents the number of bacteria, `y`, in the liquid medium `t` days after the start of the observation?
A) `y= 1/2("44,000")^t`
B) y= `2("44,000")^t`
C) `y = "44,000"(1/2)^t`
D) `y = "44,000"(2)^t`
Answer: D
Since the number of bacteria doubles every day, the relationship between `t` and `y` can be represented by an exponential equation of the form , where `a` is the number of bacteria at the start of the observation and the number of bacteria increases by a factor of `b` every `t` days. It’s given that there are `"44,000"` bacteria at the start of the observation. Therefore, `a="44,000"a = "44,000"`. It’s also given that the number of bacteria doubles, or increases by a factor of `2`, every day. Therefore, `b = 2`. Substituting `"44,000"` and `2` for `a` and `b` in the equation `y=ab^t` yields `y = 44000(2)^t`.
Question 9
`x² = -841`
How many distinct real solutions does the given equation have?
A) Exactly one
B) Exactly two
C) Infinitely many
D) Zero
Answer: D
The square of any real number cannot be negative. Since `x²` must be positive or zero for any real number `x`, there are no real values of `x` that can satisfy the equation `x² = -841`. Therefore, the equation has zero distinct real solutions.
Question 10
If `4^(8c) = root(3)(4^7)`, what is the value of `c`?
Answer: `7/24`
The expression `root(3)(4^7)` can be written with a fractional exponent as `4^(7/3)`. The equation then becomes `4^(8c)= 4^(7/3)`. Since the bases are the same, the exponents must be equal: `8c = 7/3`. To solve for `c`, divide both sides by `8`, which gives `c = 7/24`.
Question 11
In the `xy`-plane, a line with equation `2y = c` for some constant `c` intersects a parabola at exactly one point. If the parabola has equation `y= -2x^2 + 9x`, what is the value of `c`?
Answer: `81/4` or `20.25`
The given linear equation is `2y= c`. Dividing both sides of this equation by `2` yields `y=c/2`. Substituting `c/2` for `y` in the equation of the parabola yields `c/2= -2x^2 + 9x`. Adding `2x^2 - 9x` to both sides of this equation gives `2x^2 - 9x + c/2 = 0`.
Question 12

The table shows three values of `x` and their corresponding values of `g(x)`, where `g(x) = f(x) / (x + 3)` and `f` is a linear function. What is the `y`-intercept of the graph of `y = f(x)` in the `xy`-plane?
A) `(0, 36)`
B) `(0, 12)`
C) `(0, 4)`
D) `(0, -9)`
Answer: A
Use the values from the table to find points on the line `y = f(x)`.
Using `x=-27` and `g(x)=3`:
`3 = f(-27) / (-27 + 3)`, so `f(-27) = 3 xx (-24) = -72`. This gives the point `(-27, -72)`.
Using `x=-9` and `g(x)=0`:
`0 = f(-9) / (-9 + 3)`, so `f(-9) = 0`. This gives the point `(-9, 0)`.
Now, find the slope of the line passing through `(-27, -72)` and `(-9, 0)`:
`m = (0 - (-72)) / (-9 - (-27)) = 72 / 18 = 4`.
The equation for `f(x)` is `f(x) = 4x + b`. Using the point `(-9, 0)`:
`0 = 4(-9) + b`, so `b = 36`.
The `y`-intercept is `(0, 36)`.
Question 1
`k² - 53 = 91`
What is the positive solution to the given equation?
A) `144`
B) `72`
C) `38`
D) `12`
Question 2
`(55) / (x + 6) = x`
What is the positive solution to the given equation?
Question 3
A manager is responsible for ordering supplies for a shaved ice shop. The shop's inventory starts with `"4,500"` paper cups, and the manager estimates that `70` of these paper cups are used each day. Based on this estimate, in how many days will the supply of paper cups reach `"1,700"`?
A) `20`
B) `40`
C) `60`
D) `80`
Question 4
`g(x) = 11 times (1/12)^x`
If the given function `g` is graphed in the `xy`-plane, where`y = g(x)`, what is the `y`-intercept of the graph?
A) `(0, 11)`
B) `(0, 132)`
C) `(0, 1)`
D) `(0, 12)`
Question 5
`(x + 2)(x − 5)(x + 9) = 0`
What is a positive solution to the given equation?
A) `3`
B) `4`
C) `5`
D) `18`
Question 6
A rectangle has a length of `x` units and a width of `x−15` units. If the rectangle has an area of `76` square units, what is the value of `x`?
A) `4`
B) `19`
C) `23`
D) `76`
Question 7
A rectangle has an area of `155` square inches. The length of the rectangle is `4` inches less than `7` times the width of the rectangle. What is the width of the rectangle, in inches?
Question 8
The number of bacteria in a liquid medium doubles every day. There are `"44,000"` bacteria in the liquid medium at the start of an observation. Which represents the number of bacteria, `y`, in the liquid medium `t` days after the start of the observation?
A) `y= 1/2("44,000")^t`
B) y= `2("44,000")^t`
C) `y = "44,000"(1/2)^t`
D) `y = "44,000"(2)^t`
Question 9
`x² = -841`
How many distinct real solutions does the given equation have?
A) Exactly one
B) Exactly two
C) Infinitely many
D) Zero
Question 10
If `4^(8c) = root(3)(4^7)`, what is the value of `c`?
Question 11
In the `xy`-plane, a line with equation `2y = c` for some constant `c` intersects a parabola at exactly one point. If the parabola has equation `y= -2x^2 + 9x`, what is the value of `c`?
Question 12

The table shows three values of `x` and their corresponding values of `g(x)`, where `g(x) = f(x) / (x + 3)` and `f` is a linear function. What is the `y`-intercept of the graph of `y = f(x)` in the `xy`-plane?
A) `(0, 36)`
B) `(0, 12)`
C) `(0, 4)`
D) `(0, -9)`