Question 1
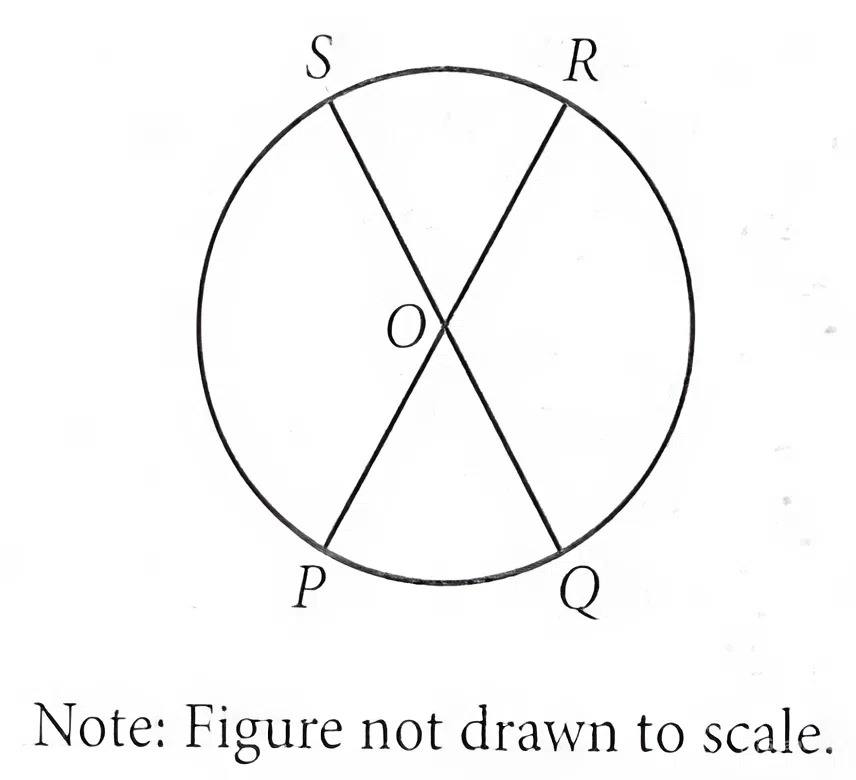 The circle shown has center `O`, circumference `144pi` and diameters `PR` and `QS`. The length of arc `PS` is twice the length of arc `PQ`. What is the length of arc `QR`?
The circle shown has center `O`, circumference `144pi` and diameters `PR` and `QS`. The length of arc `PS` is twice the length of arc `PQ`. What is the length of arc `QR`?
A) `24pi`
B) `48pi`
C) `72pi`
D) `96pi`
Mark as Complete
Mark Scheme
Question 2
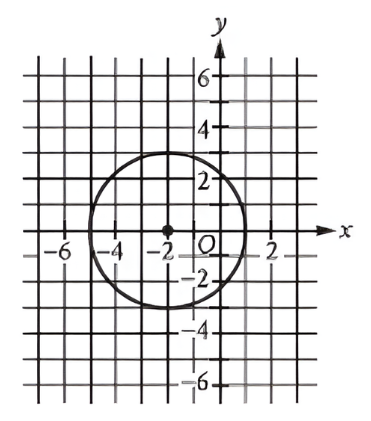
Circle `A` (shown) is defined by the equation `(x + 2)² + y² = 9`. Circle `B` (not shown) is the result of shifting circle `A` down `6` units and increasing the radius so that the radius of circle `B` is `2` times the radius of circle `A`. Which equation defines circle `B`?
A) `(x + 2)² + (y + 6)² = (4)(9)`
B) `2(x + 2)² + 2(y + 6)² = 9`
C) `(x + 2)² + (y - 6)² = (4)(9)`
D) `2(x + 2)² + 2(y - 6)² = 9`
Mark as Complete
Mark Scheme
Question 3
In the xy-plane, a circle has center `C` with coordinates `(h, k)`. Points `A` and `B` lie on the circle. Point `A` has coordinates`(h + 1, k + √102)` and `∠ACB` is a right angle. What is the length of `AB`?
A) √206
B) 2√102
C) 103√2
D) 103√3
Mark as Complete
Mark Scheme
Question 1
 The circle shown has center `O`, circumference `144pi` and diameters `PR` and `QS`. The length of arc `PS` is twice the length of arc `PQ`. What is the length of arc `QR`?
The circle shown has center `O`, circumference `144pi` and diameters `PR` and `QS`. The length of arc `PS` is twice the length of arc `PQ`. What is the length of arc `QR`?
A) `24pi`
B) `48pi`
C) `72pi`
D) `96pi`
Answer: B
Since `PR` and `QS` are diameters of the circle shown, `OS`, `OR`, `OP`, and `OQ` are radii of the circle and are therefore congruent. Since `angle SOP` and `angle ROQ` are vertical angles, they are congruent. Therefore, arc `PS` and arc `QR` are formed by congruent radii and have the same angle measure, so they are congruent arcs. Similarly, `angle SOR` and `angle POQ` are vertical angles, so they are congruent. Therefore, arc `SR` and arc `PQ` are formed by congruent radii and have the same angle measure, so they are congruent arcs.
Let `x` represent the length of arc `SR`. Since arc `SR` and arc `PQ` are congruent arcs, the length of arc `PQ` can also be represented by `x`. It's given that the length of arc `PS` is twice the length of arc `PQ`. Therefore, the length of arc `PS` can be represented by the expression `2x`. Since arc `PS` and arc `QR` are congruent arcs, the length of arc `QR` can also be represented by `2x`. This gives the expression `x + x + 2x + 2x`. Since it’s given that the circumference is `144pi`, the expression `x + x + 2x + 2x` is equal to `144pi`. Thus `x + x + 2x + 2x = 144pi`, or `6x = 144pi`. Dividing both sides of the equation by `6` yields `x = 24pi`. Therefore, the length of arc `QR` is `2(24pi)`, or `48pi`.
Question 2

Circle `A` (shown) is defined by the equation `(x + 2)² + y² = 9`. Circle `B` (not shown) is the result of shifting circle `A` down `6` units and increasing the radius so that the radius of circle `B` is `2` times the radius of circle `A`. Which equation defines circle `B`?
A) `(x + 2)² + (y + 6)² = (4)(9)`
B) `2(x + 2)² + 2(y + 6)² = 9`
C) `(x + 2)² + (y - 6)² = (4)(9)`
D) `2(x + 2)² + 2(y - 6)² = 9`
Answer: A
Circle `A` has its center at `(-2, 0)` and a radius of `√9 = 3`. Shifting it down `6` units moves the center to `(-2, -6)`.
The new radius is `2 * 3 = 6`. The equation for a circle is `(x - h)² + (y - k)² = r²`.
Substituting the new center and radius gives `(x - (-2))² + (y - (-6))² = 6²`, which simplifies to `(x + 2)² + (y + 6)² = 36`.
Since `36 = 4 xx 9`, this matches option A.
Question 3
In the xy-plane, a circle has center `C` with coordinates `(h, k)`. Points `A` and `B` lie on the circle. Point `A` has coordinates`(h + 1, k + √102)` and `∠ACB` is a right angle. What is the length of `AB`?
A) √206
B) 2√102
C) 103√2
D) 103√3
Answer: A
The distance from the center `C(h, k)` to any point on the circle is the radius. The distance from `C` to `A` is the radius `r`:
`r² = ((h + 1) - h)² + ((k + √102) - k)² = 1² + (√102)² = 1 + 102 = 103`.
So the radius is `r = √103`.
Since `∠ACB` is a right angle, triangle `ACB` is a right triangle with legs `AC`and `BC`, which are both radii of the circle. The length of `AB`is the hypotenuse. Using the Pythagorean theorem: `AC² + BC² = AB². (√103)² + (√103)² = AB² 103 + 103 = AB² 206 = AB²`
so `AB = √206`.
Question 1
 The circle shown has center `O`, circumference `144pi` and diameters `PR` and `QS`. The length of arc `PS` is twice the length of arc `PQ`. What is the length of arc `QR`?
The circle shown has center `O`, circumference `144pi` and diameters `PR` and `QS`. The length of arc `PS` is twice the length of arc `PQ`. What is the length of arc `QR`?
A) `24pi`
B) `48pi`
C) `72pi`
D) `96pi`
Question 2

Circle `A` (shown) is defined by the equation `(x + 2)² + y² = 9`. Circle `B` (not shown) is the result of shifting circle `A` down `6` units and increasing the radius so that the radius of circle `B` is `2` times the radius of circle `A`. Which equation defines circle `B`?
A) `(x + 2)² + (y + 6)² = (4)(9)`
B) `2(x + 2)² + 2(y + 6)² = 9`
C) `(x + 2)² + (y - 6)² = (4)(9)`
D) `2(x + 2)² + 2(y - 6)² = 9`
Question 3
In the xy-plane, a circle has center `C` with coordinates `(h, k)`. Points `A` and `B` lie on the circle. Point `A` has coordinates`(h + 1, k + √102)` and `∠ACB` is a right angle. What is the length of `AB`?
A) √206
B) 2√102
C) 103√2
D) 103√3